2. 中国科学院电子学研究所 微波成像技术国家重点实验室, 北京 100190;
3. 中国国际工程咨询公司, 北京 100048
2. National Key Laboratory of Science and Technology on Microwave Imaging, Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China;
3. China International Engineering Consulting Corporation, Beijing 100048, China
SAR(synthetic aperture radar)图像的绝对辐射精度对SAR定量化应用具有至关重要的影响,现有的SAR绝对辐射定标方法主要利用点目标通过“端到端”的方法实现,即在定标场布置多个已知雷达截面积(radar cross section, RCS)的标准反射器,然后对比图像功率和反射器的真实RCS得到定标常数。标准反射器自身RCS稳定性可优于0.1 dB,但考虑到角反射器制造工艺带来的RCS偏差以及数据获取与处理过程中大气、噪声等的影响,当前基于定标器的绝对定标精度约为0.4 dB[1]。此外,亚马逊热带雨林等大面积均匀分布的自然目标具有稳定的后向散射特性,其γ0的季节稳定性为0.2 dB[2-3],因此可作为对点目标定标结果的补充。然而,点目标的大面积布置和长期维护需要耗费大量的人力物力,成本较高;且点目标和热带雨林均存在地理空间的限制,只能隔一段时间照射一次,难以实现在正常完成观测任务的同时进行常态化辐射定标。
为了增加对系统传递特性的测量频次,有学者致力于在自然地物中找到更多诸如热带雨林般可用于定标的大面积均匀地物,如沙漠、海洋等,但该类地物在用于定标时对入射角、地形起伏、风速等有一定的限制,只能在特定条件下实现短期稳定[4-7]。同时,上述思路仍未解决空间局限性问题。
有学者提出永久散射体(permanent scatter, PS)和点目标结合的辐射定标方法[1, 8-10],即首先用点目标(如角反射器、雷达转发器等)对PS进行RCS标定。由于PS的RCS随时间变化很小,因此可以在点目标定标后利用PS完成图像之间的相对辐射标定。经验证,其与雷达转发器的定标差异小于0.2 dB,但该方法要求相对标定的图像地理位置相同且具有高度相似的成像几何,并且图像之间需要精确配准,PS点要一一对应,条件非常苛刻。
若能在普通的地物场景中,找到具有稳定性的散射特征量,则可将其作为定标参考,实现对SAR系统的持续监测。本文在对C波段SAR图像进行地物分类并建立散射样本库的基础上,分析发现城区的后向散射系数中值重心具有良好的时间稳定性,进而提出一种基于神经网络的城区地物精筛与散射稳定特性提取方法,为常态化的SAR辐射定标提供技术支撑。
1 散射稳定性分析总体流程本文开展SAR图像散射稳定特性分析和提取的总体流程如图 1所示。首先利用现有已精确定标的SAR图像集进行场景分类并建立不同类别的地物样本库,为后续分析提供海量的数据支撑。然后确定一个合理的能够描述散射稳定特性且能够作为定标参考的散射特征量。接着分析比较不同地物类型中该特征量的稳定性,从而优选地物类型。在此基础上,训练用于分类的神经网络,对稳定地物类型进行精细筛选,得到更加稳定的散射特性。随后对所提取的散射特征稳定性进行验证,并给出以此稳定特征为参考的辐射定标方法。

|
Download:
|
| 图 1 C波段SAR地物散射稳定性分析方法 Fig. 1 Analysis method for stability of target backscattering at C-band | |
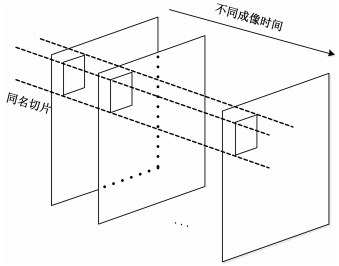
本文中所考虑的散射稳定性主要是指散射特性的时间稳定性,即是否能够在较长的时间内保持后向散射系数的恒定,这是其能够作为定标参考的重要衡量标准。为衡量某类地物样本切片的时间稳定性,引入“同名切片”的概念,定义为同一地理区域在不同时间所成图像中对应的图像样本切片,如图 2所示。时间稳定性通过同名切片的后向散射系数统计量的标准差来衡量。
|
Download:
|
| 图 2 同名切片示意图 Fig. 2 Homologue slices | |
散射样本库的建立是稳定特性分析的基础,本文利用哨兵1号数据开展样本库的构建工作,下面对数据源和样本库构建方法进行说明。
2.1 Sentinel-1数据Sentinel-1(哨兵1号)是欧空局的地球观测卫星,由搭载C波段SAR的Sentinel-1 A、Sentinel-1B两颗卫星组成。二者相互配合,可在全球实现重访周期为6 d的连续观测,提供大量多时相的观测数据。相比其他在轨雷达卫星,Sentinel-1具有较高的辐射精度,其辐射定标稳定性为0.5 dB(3σ),绝对辐射精度为1 dB(3σ)[11-12],可满足散射稳定性挖掘对SAR图像辐射精度的要求。
分析所用的图像成像于美国休斯顿地区,产品级别为L1级GRD(ground range detected),经过聚焦、多视、地距转换等处理并去除噪声。时间跨度为2015年1月到2017年9月,共33幅图像,时间间隔约30 d,详细参数如表 1所示。
|
|
表 1 Sentinel-1图像参数 Table 1 Parameters of Sentinel-1 images |
为了对大量SAR图像进行快速便捷的地物分类,本文参考已在全球范围内实现地物分类的Modis产品。Modis是搭载在美国Terra和Aqua卫星上的中分辨率成像光谱仪,其三级土地覆盖类型产品MCD12Q1综合Terra和Aqua一年的观测结果,采用有监督的决策树分类方法,按照IGBP(国际地圈生物圈计划)将地物分为17类,空间分辨率为500 m。产品使用正弦投影,在赤道处按照10°×10°的网格分幅。由于研究区域的分类信息可能分布在不同Modis分幅上,因此在使用前需要先对相关的若干个Modis图像进行拼接。
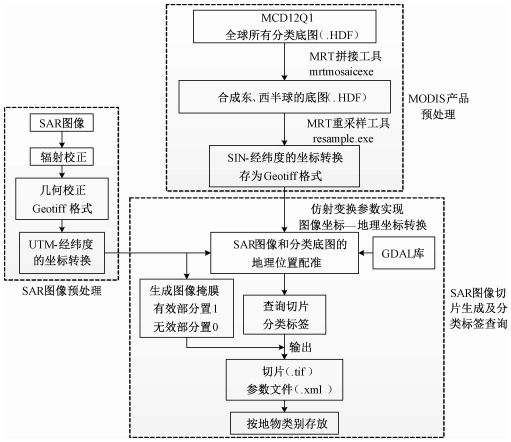
基于已有的Modis产品,本文提出一种SAR图像快速分类及切片自动提取方法,流程如图 3所示,主要包括以下3个部分:
|
Download:
|
| 图 3 地物分类及切片提取的流程图 Fig. 3 Flow chart of classification and slice extraction | |
1) Modis产品的预处理。用Modis的专用数据处理软件MRT对全球范围内的MCD12Q1产品进行拼接以实现对任意地理位置的查询,然后进行正弦投影到经纬度的坐标转换。
2) SAR图像的预处理。用Sentinel的专用数据处理软件SNAP对其进行辐射校正、几何校正以及UTM到经纬度的坐标变换,生成σ0图像。
3) SAR图像切片生成及分类标签查询。经过预处理后,Modis图像和SAR图像均转换到WGS84基准下的经纬度坐标系中,可将二者进行地理位置匹配。具体过程为:获取待分类SAR图像中每个点的经纬度信息,并在Modis产品中查找该地理位置处的分类标签,然后在SAR图像中以R×R大小为基本单位提取切片,该切片对应于MCD12Q1中的一个像素。R的计算公式为
| $ R = \left\lfloor {\frac{{{\rm{RE}}{{\rm{S}}_{{\rm{MODIS}}}}}}{{{\rm{RE}}{{\rm{S}}_{{\rm{SAR}}}}}}} \right\rfloor, $ | (1) |
式中:
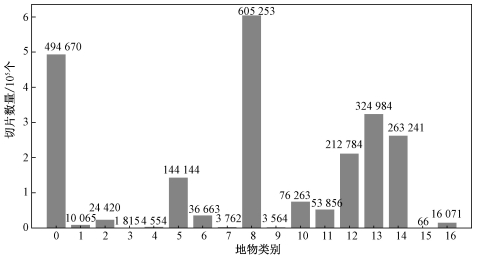
利用该方法,现已积累Sentinel-1各类地物切片总量达227万,如图 4所示。经目视检验,切片分类基本正确,但仍存在一些由于城市变迁等引起的分类误差,然而在大量数据的统计意义下,这类误差对于稳定性分析的影响可以忽略。
|
Download:
|
| 图 4 散射样本库的切片数量 Fig. 4 Slice amount in the sample database | |
在分析地物的散射稳定性之前,首先要确定一个后向散射系数的描述特征,它应该满足以下条件:1)与地物后向散射系数直接线性相关,是对后向散射系数的定量描述,最简单的就是后向散射系数的均值、中值等;2)在同类地物切片之间,该特征具有更好的稳定性。为了从统计分布模型入手选取合适的描述特征,本文选用Fisher分布进行散射统计量稳定性的理论分析,因为该模型对海面、农田、森林、城市、山区等多种类型地表区域的图像强度均具有建模适用性[13-14],其概率密度函数如下:
| $ f\left( I \right) = \frac{{\Gamma \left( {L + M} \right)}}{{\Gamma \left( L \right)\Gamma \left( M \right)}}\frac{L}{{M\mu }}\frac{{{{\left( {LI/M\mu } \right)}^{L-1}}}}{{{{\left( {1 + LI/M\mu } \right)}^{L + M}}}}, $ | (2) |
式中:L为视数,I为图像强度,M为形状参数,μ为平均强度,Γ(·)为伽马函数。
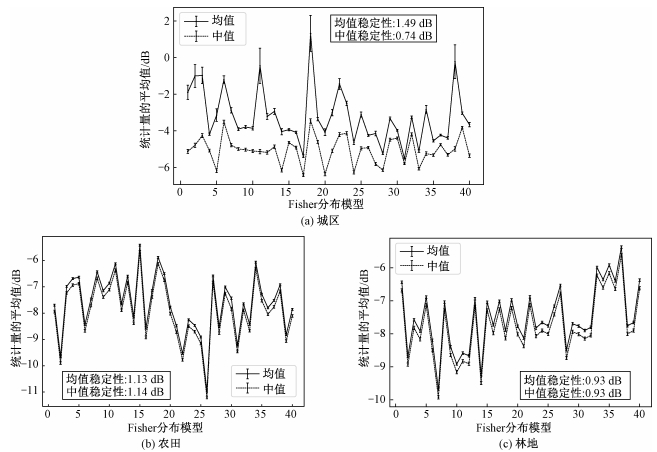
选取休斯顿地区3种典型的地物类型:城区、农田、林地,每种地类选用40个图像切片,分别用Fisher分布进行拟合,得到模型参数M和μ。对每一组拟合参数,生成3 000次Fisher分布随机数,相当于对该分布进行多次随机抽样,而每组抽样样本模拟一个地物切片中的后向散射系数。计算每组样本的均值和中值,并求出相同模型参数下,均值和中值在多次随机抽样中的平均值和标准差,如图 5所示。图中横轴代表Fisher分布40组不同的模型参数,纵轴是3 000次抽样中统计量的平均值,误差棒表示统计量的标准差。对于城区这类非均匀区域,中值的稳定性明显优于均值,而对于农田、林地等自然地物,中值和均值的稳定性接近。为适应多类地物的散射特性,本文选用统计中值作为切片后向散射系数的定量描述值。
|
Download:
|
| 图 5 Fisher分布统计量的稳定性 Fig. 5 Stability of statistics using Fisher model | |
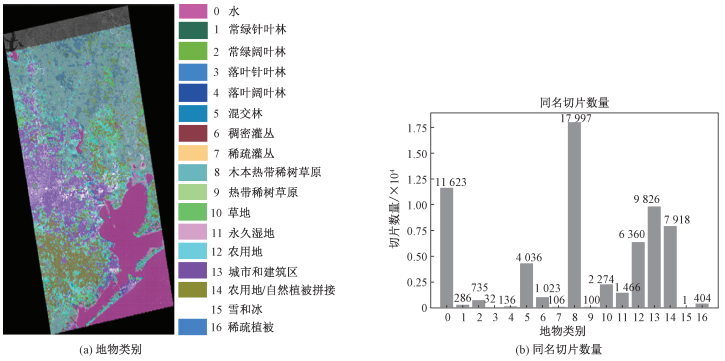
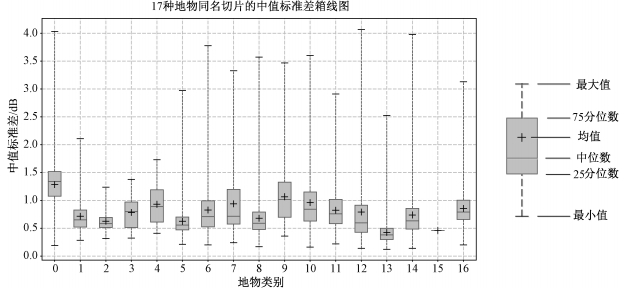
选用休斯顿地区33幅多时相图像,按照2.2节的方法将SAR图像打散为17类地物切片,并获取同名切片,Modis分类结果如图 6所示。对每一组同名切片,求出后向散射系数的中值标准差stdmedian。为评价每一类地物随时间变化的稳定性,按照类别对中值标准差统计最小值、25分位数、中值、均值、75分位数、最大值,以箱线图的形式画于图 7中。其中,同名切片中值标准差的统计量沿纵轴位置的高低代表该类地物同名切片标准差的整体大小,而沿纵轴分布的稠密程度反映该类地物切片标准差的分布集中程度。第1,3,4,7,9,15类的切片数量较少,统计意义下的结论不具有代表性,因此不参与比较。在剩余的11种地物中,第13类城市与建筑区(以下简称“城区”)箱线图的箱体最扁,位置最低,说明所有城区同名切片的中值标准差集中在一个较小的值处,平均为0.42 dB。一些植被覆盖类型如第14类农用地/自然植被拼接、第12类农用地、第10类草地等由于具有一定的生长周期,不同生长阶段的形态、含水量不同,导致其后向散射特性随季节有着较大变化;而城区中的建筑、道路、桥梁等人工目标的结构、形态不像自然地物那样易受季节的影响,所以后向散射特性随时间具有一定的稳定性。
|
Download:
|
| 图 6 同名切片的Modis分类结果 Fig. 6 Classification results of homologue slices based on Modis | |
|
Download:
|
| 图 7 各类地物的时间稳定性 Fig. 7 Temporal stability of all categories | |
城区同名切片具有很好的时间稳定性,但是基于同名切片进行稳定特征提取的方案仍对图像地理位置的匹配精度具有较高要求,存在和PS定标方法相同的局限。因此本文同名切片仅在分析过程中用来衡量地物的时间稳定性,而最终用于定标的参考值是用所有城区切片计算得到的中值平均值(称为“中值重心”)。由此用该方法定标时并不需要提取同名切片,从而降低了对地理位置匹配精度的要求。
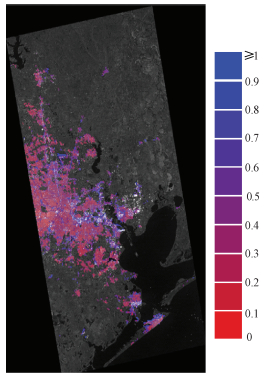
3.3 基于神经网络精细筛选的散射稳定性提升尽管城区是所有17类地物中随时间变化最稳定的类别,但是由图 7可知,城区同名切片的中值标准差在0.1~2.5 dB之间均有分布,即同为城区类别,不同切片之间仍存在随时间变化稳定/不稳定的差异。画出所有城区同名切片的中值标准差分布(图 8)并对照实物(图 9)发现,稳定城区切片在SAR图像中的整体亮度均匀,有少量强散射点,对应的实物主要为一些排布整齐的低矮居民区,房屋的高度和形状相似;不稳定城区切片在SAR图像中整体呈亮色,散射强度较大,对应的实物多为高楼林立的市中心,房屋高度形状参差不齐。
|
Download:
|
| 图 8 城区切片的标准差分布图 Fig. 8 Standard deviation distribution of urban slices | |

|
Download:
|
| 图 9 实物(来源于Google Earth) Fig. 9 Actual objects (from Google Earth) | |
由于二者存在较为明显的图像特征差异,本文采用一个二分类模型对城区切片进行精细筛选,从而选出相对更稳定的切片。其中,训练集中的正负类样本是按照城区同名切片的中值标准差stdmedian以某个阈值进行划分的。在确保正负类样本的图像特征具有区分度的前提下,为使得筛选后切片的中值重心具有尽可能好的稳定性,阈值应越小越好,但考虑到正类样本须具备一定的数量规模以保证统计意义,从图 10中的切片数量分布来看,0.3 dB是一个合适的阈值。即正类样本:stdmedian≤0.3 dB,负类样本:stdmedian>0.3 dB。

|
Download:
|
| 图 10 不同阈值处正类样本的数量分布 Fig. 10 Quantity distribution of positive samples at different thresholds | |
对于模型的分类效果,本文主要考虑查全率recall和查准率precision两个指标,计算公式如下:
| $ {\rm{recall = }}\frac{{{\rm{TP}}}}{{{\rm{TP + FN}}}}, {\rm{precusion = }}\frac{{{\rm{TP}}}}{{{\rm{TP + FP}}}}. $ | (3) |
其中,TP、FN、FP分别是模型将正类预测为正类、将正类预测为负类、将负类预测为正类的样本数。因此较高的查全率表示模型能够将大部分稳定切片筛选出来,保证最终参与计算中值重心的切片数量可以达到统计意义的要求;较高的查准率表示模型选出的正类样本大部分为稳定的城区切片,从而保证中值重心的稳定性能得到一定程度的提升。
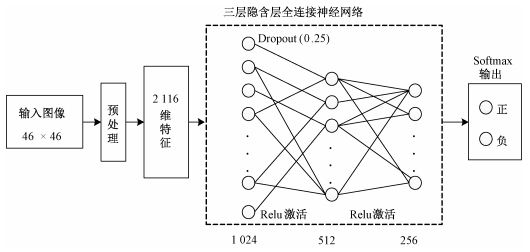
在模型选取方面,尝试支持向量机(SVM)、卷积神经网络(CNN)、全连接神经网络(FNN)等常用分类模型,三者在测试集上的平均查全率和平均查准率如表 2所示,分类效果最好的是全连接神经网络。为使得相差一个定标常数的已定标图像和未定标图像在输入分类模型时是等效的,图像经过取dB并去除均值的预处理,然后将所有图像像素作为特征输入网络。FNN网络模型如图 11所示,采用Dropout、修正线性单元(Relu)激活函数等技巧以避免过拟合并提高模型训练速度[15-16]。
|
|
表 2 不同模型的分类效果(在测试集上取平均值) Table 2 Classification results using different models |
|
Download:
|
| 图 11 全连接神经网络结构 Fig. 11 Structure of full-connected neural network | |
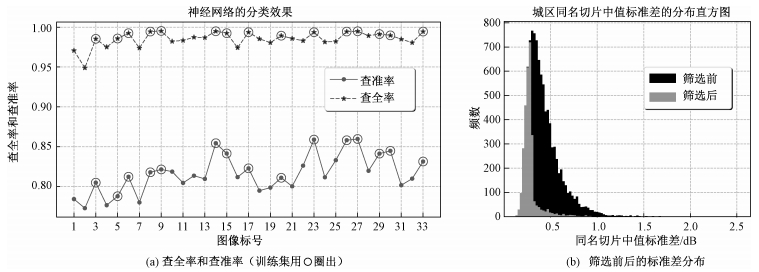
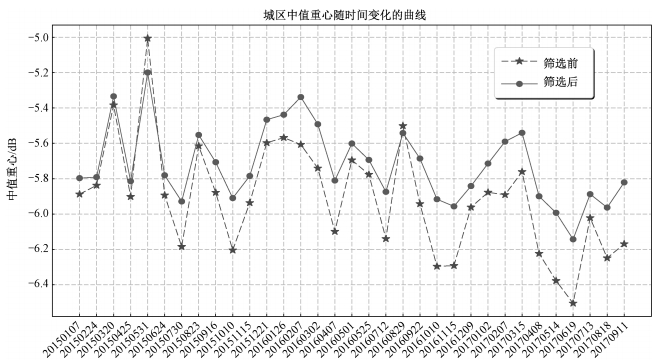
从图 12(a)可以看出,FNN模型在18幅测试场景中对稳定城区切片达到95%以上的查全率和80%以上的查准率,分类效果较好,同时也说明两类样本是可分的。从图 12(b)同名切片的中值标准差的分布来看,模型选出的正类样本的标准差大多集中在0.3 dB以内,只有少量样本大于0.3 dB,且不超过0.3 dB的样本几乎全部被分类为正,因此模型对于城区稳定城区切片有很好的筛选能力。图 13表明,经神经网络精选后城区切片的稳定性得到了有效提升,中值重心随时间变化的标准差由0.31 dB降为0.21 dB。
|
Download:
|
| 图 12 全连接神经网络的分类效果 Fig. 12 Classification results using the full-connected neural network | |
|
Download:
|
| 图 13 城区切片筛选前后的中值重心稳定性 Fig. 13 Stability of median center calculated for urban slices before and after filtering | |
为验证城区中值重心用于系统长期标定的可行性,将其散射稳定性与热带雨林的分析结果进行比较,并给出基于城区中值重心的定标常数估计方案。
4.1 热带雨林散射稳定性的分析结果热带雨林一直以来被认为是均匀稳定的自然地物,因此用Sentinel-1热带雨林的散射稳定性作为参考来衡量城区中值重心的稳定性。所用热带雨林数据采集于72.61°W~64.15°W,3.46°S~11.74°S的地理区域,包含条带模式S1~S6波位、HH和VV两种极化模式共64幅图像,时间跨度为2014年10月至2016年8月。
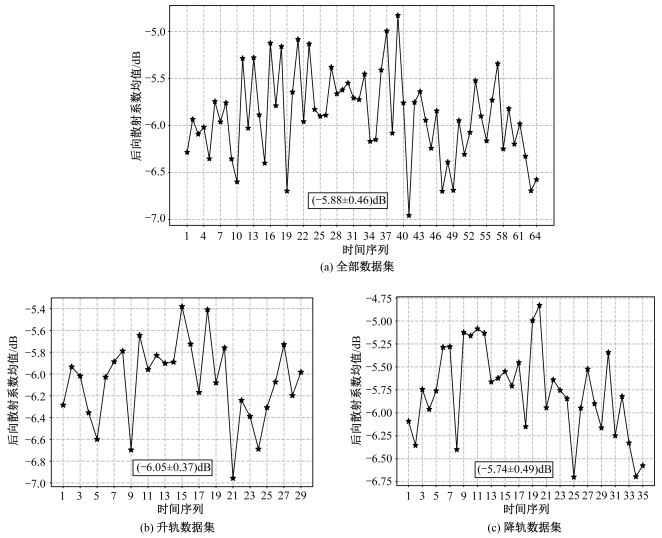
将所有热带雨林图像的后向散射系数γ0均值随时间的变化画于图 14(a)中,可以看出大部分γ0均值集中在-6.5~-5 dB之间,标准差为0.46 dB。由于卫星升、降轨情况下分别会在晚上、早上经过亚马逊热带雨林,两个时间段植被含水量的不同会对雨林后向散射系数产生较大影响,因此区分升降轨来分析雨林的γ0均值,分别如图 14(b)、14(c)所示。
|
Download:
|
| 图 14 Sentinel-1热带雨林的时间稳定性 Fig. 14 Temporal stability of Sentinel-1 rainforest data | |
升、降轨数据的γ0均值随时间变化的标准差分别为0.37和0.49 dB,升轨情况下具有更好的时间稳定性。由上述分析可知,城区切片的σ0中值重心稳定性优于热带雨林γ0均值稳定性,且和Sentinel-1自身的辐射定标精度0.33 dB(1σ)接近,因此城区中值重心可以作为一个稳定的定标参考值。
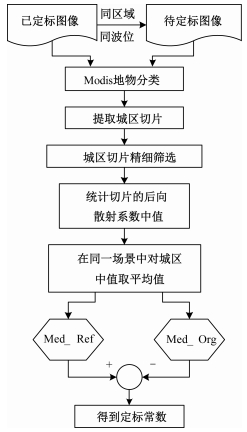
4.2 基于城区中值重心的定标常数估计方案基于精选后城区中值重心的稳定性,可以提出一种绝对定标常数估计方案,流程如图 15所示。对于一组同区域同波位的多时相SAR图像集,首先根据Modis产品对SAR图像进行地物分类,并提取第13类城区切片;然后用神经网络模型对所有城区切片进行二分类,对分类结果为正的稳定城区切片计算中值重心;最后根据已定标图像和待定标图像的中值重心之差计算绝对定标常数。
|
Download:
|
| 图 15 定标流程图 Fig. 15 Flow chart of calibration | |
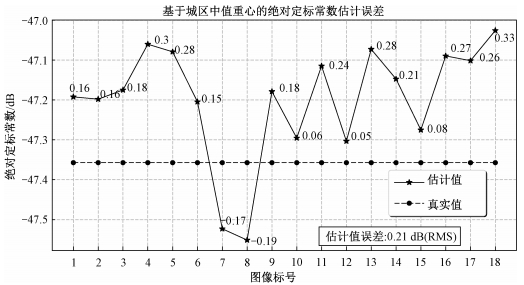
用哨兵1号休斯顿地区另外18幅未参与模型训练的图像对上述定标方案进行测试,以图像强度作为输入,将系统提供的定标常数-47.36 dB作为真值,得到定标常数的估计结果如图 16所示。估计误差在0.05~0.33 dB,均方根(RMS)为0.21 dB,精度较好。因此基于同区域同波位多时相图像集对该波位定标常数进行长期监测和校正的方案是可行的,且和永久散射体的相对辐射定标精度相当。与后者基于同名PS点的思路相比,该方案利用同类地物的散射稳定性进行定标,不要求图像之间的精确配准,且更有利于后续将定标方案在不同区域以及不同波位进行推广。
|
Download:
|
| 图 16 定标常数的估计误差 Fig. 16 Estimation error of calibration constant | |
本文针对C波段SAR图像,提出一种散射稳定特性的分析与提取方法。基于哨兵1号休斯顿S3波位的多时相图像集,在利用Modis产品构建不同类别地物散射样本库的基础上,分析发现城区的散射稳定性优于其他地物类别。通过神经网络对城区切片的进一步精细筛选,最终得到城区切片后向散射系数中值重心的时间稳定性为0.21 dB,与系统自身的绝对辐射精度相当。经验证,城区中值重心的时间稳定性优于热带雨林,且该特征用于定标常数估计时的均方根误差为0.21 dB,可以作为系统长期标定的参考值。
| [1] |
Giudici D, Villa A, Recchia L, et al. Long term PS-CAL analysis of ERS and ASAR data and comparison to other calibration techniques[C]//Proceedings of the European Conference on Synthetic Aperture Radar. Berlin: VDE, 2014: 1361-1364.
|
| [2] |
云日升, 郭伟. 亚马逊热带雨林星载SAR天线方向图获取与应用[J]. 测试技术学报, 2008, 22(4): 301-306. DOI:10.3969/j.issn.1671-7449.2008.04.005 |
| [3] |
Hawkins R, Attema E, Crapolicchio R, et al. Stability of Amazon backscatter at C-Band:spaceborne results from ERS-1/2 and RADARSAT-1[J]. Proceedings of the CEOS SAR Workshop, 2000, 450: 99-108. |
| [4] |
Ridley J, Strawbridge F, Card R, et al. Radar backscatter characteristics of a desert surface[J]. Remote Sensing of Environment, 1996, 57(2): 63-78. DOI:10.1016/0034-4257(96)00018-1 |
| [5] |
Horstmann J, Lehner S. A new method for radiometric calibration of spaceborne SAR and its global monitoring[C]//International Geoscience and Remote Sensing Symposium. New York: IEEE, 2002: 620-622.
|
| [6] |
徐曦煜, 刘和光, 杨双宝. 星载雷达高度计沙漠散射特性及定标方法研究[J]. 遥感技术与应用, 2016, 31(5): 893-899. |
| [7] |
丁岩, 洪峻, 明峰, 等. 利用海面风场测量定标常数方法实验研究[J]. 国外电子测量技术, 2010, 29(6): 68-71. DOI:10.3969/j.issn.1002-8978.2010.06.020 |
| [8] |
Rizzoli P, Giudici D, D'Aria D, et al. Permanent scatterers for SAR sensor calibration[C]//European Conference on Synthetic Aperture Radar. VDE, 2008: 1-4.
|
| [9] |
D'Aria D, Ferretti A, Guarnieri A M, et al. SAR calibration aided by permanent scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2076-2086. DOI:10.1109/TGRS.2009.2033672 |
| [10] |
Iannini L, Guarnieri A M. A PS-based approach for the calilbration of spaceborne polarimetric SAR systems[C]//IEEE International Symposium on Geoscience and Remote Sensing. New York: IEEE, 2012: 3297-3300.
|
| [11] |
Schwerdt M, Schmidt K, Ramon N T, et al. Independent verification of the Sentinel-1A system calibration[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3): 994-1007. DOI:10.1109/JSTARS.2015.2449239 |
| [12] |
Schwerdt M, Schmidt K, Ramon N T, et al. Independent system calibration of Sentinel-1B[J]. Remote Sensing, 2017, 9(6): 511-544. DOI:10.3390/rs9060511 |
| [13] |
李永晨, 刘浏. SAR图像统计模型综述[J]. 计算机工程与应用, 2013, 49(13): 180-186. DOI:10.3778/j.issn.1002-8331.1301-0356 |
| [14] |
Tison C, Nicolas J M, Tupin F, et al. A new statistical model for Markovian classification of urban areas in high-resolution SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2046-2057. DOI:10.1109/TGRS.2004.834630 |
| [15] |
李松, 魏中浩, 张冰尘, 等. 深度卷积神经网络在迁移学习模式下的SAR目标识别[J]. 中国科学院大学学报, 2018, 35(1): 75-83. |
| [16] |
杜康宁, 邓云凯, 王宇, 等. 基于多层神经网络的中分辨SAR图像时间序列建筑区域提取[J]. 雷达学报, 2016, 5(4): 410-418. |
 2019, Vol. 36
2019, Vol. 36 


