图像配准是一项非常重要的图像预处理技术。随着数字图像处理的发展,图像配准技术已经被广泛应用于高分辨率图像生成[1]、医学图像对齐[2]、高精度3D重建[3]、遥感图像变化检测、多源图像融合等领域。这些关键领域中,需要高精度的图像配准,即亚像素级的图像配准。现有的亚像素级图像配准算法主要分为3类[4-5]:基于插值的方法[6-8]、解最优化问题法[9-10]和扩展的相位相关法[2, 11-13]。其中,基于插值的方法采用插值技术对相似性函数或者图像进行插值重采样,以插值后的最大值位置作为配准位置,以此达到亚像素的精度。Guizar-Sicairos等[7]对相似形函数内插法进行快速改进;Yousef等[8]在此基础上进一步提高速度,在保证配准精度的同时大大减少计算复杂度。本文在此将Yousef等[8]提出的快速相似性函数内插法称为fast-SSDFT方法。解最优化问题法的目标函数为衡量两幅待配准图像之间相似程度的函数,支持各种变换模型,具有参数选择灵活,计算精度高的特点,但是其计算量非常大,收敛概率和得到全局最优解的概率也需要提高。基于相位相关的方法利用傅里叶变换的特性,将时域上的平移量转化为求解频域上的相位相关,具有精度高、对噪声鲁棒和计算复杂度低等优点。
目前所有扩展的相位相关法都是基于傅里叶变换的平移特性,即两幅待配准的图像在空间域上存在平移,转换到频域上则表现为线性相位,通过对频域上线性相位的求解来获得空间域上的平移量。传统的相位相关法直接将归一化互功率谱矩阵进行傅里叶反变换,通过判断冲激函数的峰值位置得到平移参数的值,但是这种方法只能得到整数像素值。Hoge[11]提出,通过对归一化互功率谱矩阵进行奇异值分解,用最大奇异值所对应的奇异向量估算出平移量,可以达到亚像素的精度。该方法通过选取最大奇异值,抛弃小的奇异值,起到对噪声过滤的作用,因此该方法对平移参数的估计具有较高的精度。另外为了求得亚像素精度的平移量,需要对得到的奇异向量的相位值进行一维相位解缠,然后用最小二乘法估计出平移量。Tong等[12]利用Ransac算法[14]替代最小二乘法对解缠后的相位值进行估计,在噪声较大的情况下,Ransac算法能够滤除噪声带来的异常值,使得估计出的平移参数精度更高。Feng等[13]针对低信噪比的图像提出一种鲁棒的亚像素配准算法,该算法通过计算两幅图像的互相关系数[15]的质心得到精确的平移参数,从而达到亚像素的配准精度,本文在此将其称为CC_centriod方法。
在理想无噪的情况下,缠绕相位具有一定的周期性,可以通过积分的方法进行相位解缠。通过积分的方法求得真实相位具有一个前提,即相邻两个像元间的真实相位差的绝对值要小于π[16],但是如果两幅图像之间的平移量超过某个阈值或者受噪声影响时,所得到的一维缠绕相位向量相邻的真实相位差的绝对值会超出π,因此传统的积分法进行相位解缠就会变得不再适用。本文提出一种改进的相位解缠方法对传统积分法得到的结果进行校正,改进的算法可以避免积分法受到此前提和噪声的影响,使得估计出的平移参数更精确。本文把基于奇异值分解(SVD)的相位相关法结合改进的相位解缠方法称为SVD-IIM(SVD-improved integral method)。
1 基于SVD分解的相位相关法 1.1 方法原理和流程令x0和y0表示两幅大小为M×N的图像之间在行方向和列方向上的平移量,可以表示成
| $ g\left( {x,y} \right) = f\left( {x - {x_0},y - {y_0}} \right). $ | (1) |
式中:f(x, y)和g(x, y)为二维离散函数,其中变量x=1, 2, 3, …, M和变量y=1, 2, 3, …, N。根据傅里叶变换的性质可以得到
| $ G\left( {u,v} \right) = F\left( {u,v} \right)\exp \left\{ { - {\rm{j}}2{\rm{ \mathsf{ π} }}\left( {u{x_0}/M + v{y_0}/N} \right)} \right\}. $ | (2) |
式中:F(u, v)和G(u, v)分别是f(x, y)和g(x, y)的二维离散傅里叶变换函数,其中变量u=1, 2, 3, …, M和变量v=1, 2, 3, …, N。因此可以得到归一化互功率谱函数Q(u, v)
| $ \begin{array}{l} Q\left( {u,v} \right) = \frac{{G\left( {u,v} \right)F{{\left( {u,v} \right)}^ * }}}{{\left| {G\left( {u,v} \right)F{{\left( {u,v} \right)}^ * }} \right|}}\\ \;\;\;\;\;\;\;\;\;\;\; = \exp \left\{ { - {\rm{j}}2{\rm{ \mathsf{ π} }}\left( {u{x_0}/M + v{y_0}/N} \right)} \right\}. \end{array} $ | (3) |
式中:*代表共轭,传统的相位相关法直接计算归一化互功率谱函数Q(u, v)的傅里叶反变换:
| $ Q\left( {x,y} \right) = \delta \left( {x - {x_0},y - {y_0}} \right). $ | (4) |
在理想情况下,归一化互功率谱矩阵Q在理论上是一个秩为1的矩阵,因此归一化互功率谱函数Q(u, v)可以进行如下分解:
| $ \begin{array}{l} Q\left( {u,v} \right) = \exp \left\{ { - {\rm{j}}2{\rm{ \mathsf{ π} }}\left( {u{x_0}/M + v{y_0}/N} \right)} \right\}\\ \;\;\;\;\;\;\;\;\;\;\; = \exp \left\{ { - {\rm{j}}2{\rm{ \mathsf{ π} }}u{x_0}/M} \right\}\exp \left\{ { - {\rm{j}}2{\rm{ \mathsf{ π} }}v{y_0}/N} \right\}\\ \;\;\;\;\;\;\;\;\;\;\; = {\mathit{\boldsymbol{q}}_{{x_0}}}\left( u \right)\mathit{\boldsymbol{q}}_{{y_0}}^{\rm{H}}\left( v \right). \end{array} $ | (5) |
式中:H代表共轭转置,令向量qx0和qy0为:
| $ {\mathit{\boldsymbol{q}}_{{x_0}}} = {\left( {{{\rm{e}}^{ - {\rm{j}}\left( {2{\rm{ \mathsf{ π} }}/M} \right){x_0}}},{{\rm{e}}^{ - {\rm{j}}\left( {2{\rm{ \mathsf{ π} }}/M} \right)2{x_0}}}, \cdots ,{{\rm{e}}^{ - {\rm{j}}\left( {2{\rm{ \mathsf{ π} }}/M} \right)M{x_0}}}} \right)^{\rm{T}}}, $ | (6) |
| $ {\mathit{\boldsymbol{q}}_{{y_0}}} = {\left( {{{\rm{e}}^{{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}/N} \right){y_0}}},{{\rm{e}}^{{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}/N} \right)2{y_0}}}, \cdots ,{{\rm{e}}^{{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}/N} \right)N{y_0}}}} \right)^{\rm{T}}}. $ | (7) |
因此归一化互功率谱矩阵Q可以表示为
| $ \mathit{\boldsymbol{Q}} = {\mathit{\boldsymbol{q}}_{{x_0}}} * \mathit{\boldsymbol{q}}_{{y_0}}^{\rm{H}}. $ | (8) |
但是,在一般情况下,Q并不是一个秩为1的矩阵,因此文献[11]提出可以通过对Q矩阵进行SVD分解,用最大奇异值和相对应的奇异向量对Q进行秩1估计,由于奇异值最大的分量受噪声影响较小,因而秩1估计可以起到抑制噪声的作用。对Q进行秩1估计:
| $ \mathit{\boldsymbol{Q}} \approx {\mathit{\boldsymbol{u}}_1} * {\sigma _1} * \mathit{\boldsymbol{v}}_1^{\rm{H}}. $ | (9) |
式中:σ1为最大的奇异值,u1和v1为σ1所对应的奇异向量,因此有u1≈qx0和v1≈qy0。对u1和v1进行相位解缠,得到解缠后的相位px和py,并用最小二乘法拟合px和py,得到px和py的斜率kx和ky,通过得到的斜率最终求得平移参数:
| $ {x_0} = - \frac{{{k_x}M}}{{2{\rm{ \mathsf{ π} }}}},{y_0} = - \frac{{{k_x}N}}{{2{\rm{ \mathsf{ π} }}}}. $ | (10) |
如图 1所示的流程图,为减弱边缘效应的影响,对待配准的图像f(x, y)和g(x, y)分别进行Black窗处理后,再计算其相位相关矩阵Q。为进一步减弱频谱混叠和边缘效应的影响,需要滤除Q矩阵中的高频分量和幅度值小于特定阈值的频率分量。以直流分量为中心,以0.3N(N代表图像短边长度)为半径,滤除距离直流分量中心在此半径之外的高频分量;计算直流分量周围5×5邻域的幅度平均值,并乘以因子0.01~0.05,作为阈值,滤除小于此阈值的频率分量[12]。然后对Q进行SVD分解并按照式(9)对其进行秩1估计,得到最大奇异值所对应的奇异向量u1和v1,用积分法对u1和v1的相位值进行相位解缠,并用最小二乘法估计出解缠后相位的斜率kx和ky,最后利用式(10)计算得到平移参数x0和y0。

|
Download:
|
| 图 1 基于SVD分解的相位相关法流程图 Fig. 1 Flow chart of phase correlation method based on SVD | |
在理想情况下,图像的采样率满足Nyquist采样定理,采样频率必须大于信号最高频率的2倍,解缠相位中相邻像素点之间的相位差值不可能超过半个周期,当满足此条件时必然能通过积分法,由缠绕相位解缠出正确的真实相位值。令ϕ(m)为周期缠绕前的真实相位值,
| $ \omega \left( {\phi \left( m \right)} \right) = \varphi \left( m \right) = \phi \left( m \right) = 2{\rm{ \mathsf{ π} }}k\left( m \right). $ | (11) |
其中-π < ω(ϕ(m)) < π,得到属于(-π, π)的缠绕相位
| $ \Delta \phi \left( m \right) = \phi \left( {m + 1} \right) - \phi \left( m \right). $ | (12) |
由于真实相位值中相邻像素点之间的相位差值不可能超过半个周期,所以有
| $ - {\rm{ \mathsf{ π} }} < \Delta \phi \left( m \right) < {\rm{ \mathsf{ π} }}. $ | (13) |
对相邻缠绕相位也进行差分运算得
| $ \begin{array}{l} \Delta \varphi \left( m \right) = \varphi \left( {m + 1} \right) - \varphi \left( m \right) = \Delta \phi \left( m \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;2{\rm{ \mathsf{ π} }}\Delta k\left( m \right). \end{array} $ | (14) |
对该相位差使用缠绕算子得
| $ {\rm{ \mathsf{ π} }}\left( {\Delta \varphi \left( m \right)} \right) = \Delta \varphi \left( m \right) + 2{\rm{ \mathsf{ π} }}\Delta k\left( m \right) + 2{\rm{ \mathsf{ π} }}k'\left( m \right). $ | (15) |
根据缠绕算子ω的定义,ω(Δ
| $ \Delta k\left( m \right) + k'\left( m \right) = 0. $ | (16) |
所以可将式(15)简化为
| $ \omega \left( {\Delta \varphi \left( m \right)} \right) = \Delta \phi \left( m \right). $ | (17) |
因此最终的真实相位可以表示成
| $ \phi \left( m \right) = \phi \left( 0 \right) + \sum\limits_{n = 0}^{m - 1} {\omega \left( {\Delta \varphi \left( n \right)} \right)} . $ | (18) |
从以上推导可以看出,使用积分法进行相位解缠依赖于一个重要的前提,即真实相位中相邻像素点之间的相位差值必须在(-π, π)范围内。而在实际遥感图像配准应用中,由于有地形突变、相位混叠、平移量较大等各种因素的存在,相位信息中将会引入噪声,在计算解缠相位的过程中,并不确定式(13)是否成立,所以通过积分法即式(18)计算所得到的相位值只是相位的估计值,其准确性并不能保证[17]。
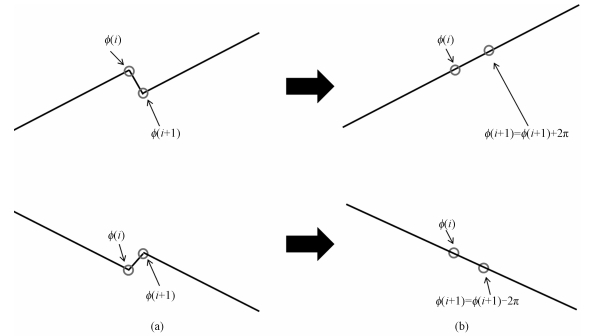
1.3 改进的相位解缠方法在使用积分法进行相位解缠时,式(18)中的缠绕算子ω会将缠绕相位差折叠到区间(-π, π)里,当真实相位差的绝对值大于π时,则会出现2kπ(k≠0)的误差(此误差在大多数情况下为2π),因此本文提出一种改进算法,能够针对这个误差进行校正。以估计平移参数x0为例,首先利用积分法对u1进行相位解缠得到解缠相位的初始结果px,根据式(6)可知,在理想状态下px是线性递增或递减的直线,如果px不满足这样一个递增或递减的趋势,那么本文就认为有必要对其进行校正处理。利用最小二乘法估计初始结果px的斜率,得到初始斜率kx1,虽然初始斜率kx1和真实斜率存在一定误差,但是已经足够描述递增或递减的趋势,因此令kx1为趋势斜率,对px进行校正。如果px中相邻相位之差通过加上或者减去2π的误差校正之后更符合趋势斜率,那么执行此校正操作,否则不进行校正。完成一次px的校正之后,需要用最小二乘法重新估计px的斜率,得到新的趋势斜率,直到前后趋势斜率不发生变化时,完成校正。最后按照式(10)利用稳定的趋势斜率精确计算出平移参数x0。
如图 2所示,如果当真实相位差的绝对值大于π时,使用积分法进行相位解缠会出现图 2(a)所示的现象,如果对ϕ(i+1)进行加上或减去2π的校正操作后更符合趋势斜率kx,那么执行此校正操作,使得校正后的ϕ(i+1)-ϕ(i)更符合趋势斜率,如图 2(b)所示。
|
Download:
|
| 图 2 相位校正示意图 Fig. 2 Schematic of phase correlation | |
本文选取的实验数据为高分2号(GF-2)卫星和资源3号(ZY-3)卫星的高分辨率多光谱图像数据(部分图像数据如图 3所示),分别进行校正效果实验和配准精度对比实验。其中校正效果实验主要对比传统积分法和改进的相位解缠方法对缠绕相位的解缠效果以及相应的配准精度,配准精度对比则实验对比在不同的平移量、加入不同大小的高斯白噪声、不同混叠情况下,本文所提SVD-IIM方法与已有的SVD方法[11]、SVD-RANSAC方法[12],CC-centriod[13]方法和fast-SSDFT[8]方法这4种方法的配准精度。

|
Download:
|
| 图 3 GF-2数据(a,b)和ZY-3数据(c,d) Fig. 3 Imagery of GF-2(a, b) and ZY-3(c, d) | |
对上文所述的高分2号数据在光谱维上取均值得到其灰度图像,在其中选取一幅大小为1 280像素×1 280像素的原始参考图像,如图 4(a)所示。将其在原灰度图像上分别在行方向平移541个像素和在列方向平移548个像素,得到另一幅平移后的原始待配准图像,如图 4(b)所示。那么这两幅灰度图像的平移关系为(541, 548),分别对两幅图像进行10倍降采样得到两幅大小为128像素×128像素的图像,如图 4(c)和4(d)所示,因此其平移关系变为(54.1, 54.8)[18]。

|
Download:
|
| 图 4 原始配准图和10倍降采样后的配准图 Fig. 4 Original images and images after 10 times downsampling used for registration | |
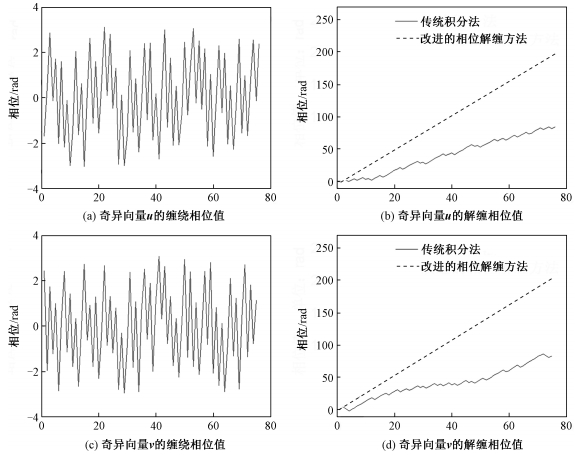
按照图 1所示的流程计算图 4(c)和图 4(d)的归一化互功率谱矩阵Q(u, v),并滤除其中的高频分量和小于特定阈值的频率分量,再对Q矩阵进行SVD分解得到最大奇异值对应的奇异向量u和v,分别利用传统积分法和改进的相位解缠方法对u和v的相位进行相位解缠。利用最小二乘法分别对图 5(b)、5(d)所示的解缠相位值的斜率进行估计,其配准结果如表 1所示,显然传统积分法的误差远远大于改进的相位解缠方法的误差。由图 5(b)、5(d)可以看出,改进的相位解缠算法能对传统积分法得到的结果进行很好的校正,因此当参考图像和待配准图像之间平移量较大时,即当相邻像素点之间相位差的绝对值接近或超过p时,利用传统的积分法相位解缠得到的结果并不可靠,而经过改进的相位解缠方法可以精确地估计出平移参数。
|
Download:
|
| 图 5 相位解缠结果示意图 Fig. 5 Schematic of the phase unwrapping results | |
|
|
表 1 传统积分法和改进相位解缠方法配准精度比较 Table 1 Precision comparison between the traditional integral method and the improved phase unwrapping method |
对上文所述的高分2号数据和资源3号数据在光谱维上取均值,利用得到的灰度图像进行配准精度对比试验,选取大小为1 280像素×1 280像素的子图为原始参考图像,以其为基准进行不同程度的平移,得到原始待配准图像。分别对原始参考图像和原始待配准图像进行10倍降采样得到实验所用的大小为128像素×128像素的配准图像。图 6和图 7为本文提出的SVD-IIM方法与其他4种方法分别在高分2号数据和资源3号数据上进行的对比结果。其中图 6(a)、6(d)和图 7(a)、7(d)为对于不同平移量的绝对误差对比示意图,其中图 6(a)和图 7(a)平移量为57~62个像素,图 6(d)和图 7(d)平移量为55~60个像素,步长均为0.1个像素;图 6(b)、6(e)和图 7(b)、7(e)为在加入不同高斯白噪声情况下的绝对误差对比示意图,将配准图像归一化至0~256,加入标准差为6~10的高斯白噪声,真实平移量为(59.4, 7.8);对待配准图减采样之前的原图进行不同程度的高斯模糊可以模拟不同情况下的混叠,而高斯模糊等价于低通滤波器[2],图 6(c)、6(f)和图 7(c)、7(f)为在不同混叠程度下的绝对误差对比示意图,高斯模糊窗大小为25×25,模糊因子为高斯函数的标准差, 真实平移量为(59.4, 7.8)。图中所有绝对误差为100幅随机选取的待配准图像配准误差的平均值。

|
Download:
|
| 图 6 GF-2数据配准精度对比图 Fig. 6 The contrast diagram of GF-2 data registration accuracy | |

|
Download:
|
| 图 7 ZY-3数据配准精度对比图 Fig. 7 The contrast diagram of ZY-3 data registration accuracy | |
如图 6(a)~6(c)和图 7(a)~7(c)所示,对于不同的平移量、加入不同大小的高斯白噪声、不同混叠情况下,本文提出的SVD-IIM方法的误差都在0附近,而原有的SVD方法和SVD-RANSAC方法的误差都在10个像素以上,因此可以进一步确定在平移量较大时传统积分法得到的相位解缠结果是错误的,而改进的相位解缠方法所得到的结果是可靠的,并且精度较高。
图 6(d)~6(f)和图 7(d)~7(f)对比在不同平移量,加入不同高斯白噪声,不同混叠情况下的3种方法的配准精度,可以看出本文提出的SVD-IIM方法的误差相比于CC-centriod方法和fast-SSDFT方法的误差更小,并且更稳定。对于较大平移量的配准问题,参考图像和待配准图像间存在较大的非匹配区域,这些非匹配区域的信息在估计平移参数时如同噪声,因此在存在大量噪声的情况下,本文提出的SVD-IIM方法可以将配准精度控制在0.1个像素范围内。
3 结束语本文针对基于奇异值分解(SVD)的相位相关法中传统积分法进行相位解缠的可靠性问题,利用线性相位单调变化的特性,提出一种改进的相位解缠方法,对传统积分法得到的结果进行校正,可以精确得到真实相位值,使得对于两幅平移量较大的待配准图像可以稳定并准确地估计出其平移参数。本文用真实光学图像的实验验证了本文提出的SVD-IIM方法在配准问题上相比于原有的SVD方法、SVD-RANSAC方法、CC-centriod方法和fast-SSDFT方法更具鲁棒性和准确性,具有重要的应用价值。
| [1] |
Vandewalle P, Süsstrunk S, Vetterli M. A frequency domain approach to registration of aliased images with application to supper-resolution[J]. Eurasip Journal on Advances in Signal Processing, 2006(1): 1-14. |
| [2] |
Stone H S, Orchard M T, Chang E, et al. A fast direct Fourier-based algorithm for subpixel registration of images[J]. IEEE Trans on Geoscience and Remote Sensing, 2001, 39(10): 2235-2243. DOI:10.1109/36.957286 |
| [3] |
Muquit M A, Shibahara T. A high-accuracy passive 3D measurement system using phase-based image matching[J]. Ieice Transactions on Fundamentals of Electronics Communications and Computer Sciences, 2006, 89(3): 686-697. |
| [4] |
黎俊, 彭启民, 范植华. 亚像素级图像配准算法研究[J]. 中国图像图像学报, 2008, 13(11): 2070-2075. |
| [5] |
卢浩, 刘团结, 尤红建. 亚像素级的图像配准方法[J]. 国外电子测量技术, 2012, 31(4): 45-49. DOI:10.3969/j.issn.1002-8978.2012.04.013 |
| [6] |
Tian Q, Huhns M N. Algorithms for subpixel registration[J]. Computer Vision, Graphics, and Image Processing, 1986, 35(2): 220-233. DOI:10.1016/0734-189X(86)90028-9 |
| [7] |
Guizar-Sicairos M, Thurman S T, Fienup J R. Efficient subpixel image registration algorithms[J]. Optics Letters, 2008, 33(2): 156-158. |
| [8] |
Yousef A, Li J, Karim M. High-speed image registration algorithm with subpixel accuracy[J]. IEEE Signal Processing Letters, 2015, 22(10): 1796-1800. DOI:10.1109/LSP.2015.2437881 |
| [9] |
Thevenaz P, Unser M. Optimization of mutual information for multiresolution image registration[J]. IEEE Transaction on Image Processing, 2000, 9(12): 2083-2099. DOI:10.1109/83.887976 |
| [10] |
徐宝昌, 陈哲, 赵龙. 一种改进的最小二乘景象匹配算法[J]. 北京航空航天大学学报, 2005, 31(8): 848-852. DOI:10.3969/j.issn.1001-5965.2005.08.005 |
| [11] |
Hoge W S. A subspace identification extension to the phase correlation method[J]. IEEE Trans on Medical Imaging, 2003, 22(2): 277-280. |
| [12] |
Tong X, Ye Z, Xu Y, et al. A noval subpixel phase correlation method using singular value decomposition and unified random sample consensus[J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 63(3): 207-224. |
| [13] |
Feng S, Deng L, Shu G, et al. A subpixel registration algorithm for low PNSR images[C]//2012 IEEE fifth International Conference on Advanced Computational Intelligence, Nanjing, 2012: 626-630.
|
| [14] |
Fischler M A, Bolles R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[M]. United States of America: ACM, 1981: 726-740.
|
| [15] |
Zitová B, Flusser J. Image registration methods:a survey[J]. Image and Vision Computing, 2003, 21(11): 977-1000. DOI:10.1016/S0262-8856(03)00137-9 |
| [16] |
Itoh K. Analysis of the phase unwrapping algorithm[J]. Applied Optics, 1982, 21(14): 2470. DOI:10.1364/AO.21.002470 |
| [17] |
邓晓龙. InSAR相位解缠算法研究[D].哈尔滨: 哈尔滨工业大学, 2013.
|
| [18] |
Foroosh H, Zerubia J B, Berthod M. Extension of phase correlation to subpixel registration[J]. IEEE Transactions on Image Processing, 2002, 11(3): 188-200. |
 2019, Vol. 36
2019, Vol. 36 


