随着近30年遥感领域的迅猛发展,光学遥感图像的空间分辨率和数量都有了巨大提高[1],对海量的遥感光学图像进行色彩校正是一个重要的问题。无论是Google地球上的遥感图像,还是中国的GF系列卫星图像,都存在颜色失真的情况。如图 1所示,图 1(a)是GF-2号卫星遥感图像,受到大气条件及传感器的影响,颜色产生失真;图 1(b)是经过颜色校正后的图像,颜色与真实地物相吻合,可进一步用于图像分割、目标检测与识别等应用;图 1(c)为Google地球上的多幅图像拼接处,可以看到交界处的颜色差异十分明显,且右半部分明显偏色。可见对海量遥感光学图像进行大规模的自动化颜色校正仍是一个有待解决的重要问题。

|
Download:
|
| 图 1 遥感光学图像的色彩失真 Fig. 1 Color distortion in remote sensing image | |
目前已有的色彩校正方法可以分为3类:颜色迁移法、经验统计法和基于物理模型的方法。颜色迁移法在校正每一幅图时,需要一幅参考图像,将参考图像的颜色直方图作为基准,对原图进行校正,从而得到与参考图像类似的颜色分布,如2008年Fecker等[2]改进直方图迁移,用它来补偿视频的颜色偏移;Kim和Pollefeys[3]考虑渐晕效应,从而更好地设计颜色迁移函数。然而在对海量的遥感图像进行校正时,无法对每幅图都获取参考图像,故此方法无法实现大量图像的自动化校正。
经验统计法以图像中各种稳定统计量的经验值作为依据,对图像进行颜色校正。此类方法大多来自于图像处理领域,如1980年Buchsbaum[4]提出零阶统计方法,即假设图像的平均反射率为灰色,从而校正图像。2007年J.van de Weijer等[5]提出一阶以及更高阶的统计方法,使用空间梯度或更高阶统计量代替简单的平均值。此外,2012年Hirakawa等[6]提出基于滤波器组的校正方法,2014年Cheng等[7]使用主成分分析——PCA(principal component analysis)进一步改进统计模型。然而这些方法都基于摄影照片的统计经验,摄影照片和遥感光学图像的颜色失真机理有很大区别,目前此类方法对遥感图像的色彩校正效果还有待提高。
基于物理模型的方法源于大气校正算法,此类方法以地物的地表反射率作为真实颜色,而卫星传感器获取的图像包含大气的影响,此类方法通过估计图像获取时的各项大气参数,基于大气传输模型计算大气的影响,从而从图像中除去这部分影响,得到颜色真实的地表反射率图像。如典型的FLAASH(fast line-of-sight atmospheric analysis of spectral hypercubes)大气校正方法[8],使用MODTRAN模型估计图像中的水汽和气溶胶参数,再加上大气模型和水汽反演模型,计算出大气的影响,从而得到地表反射率图像。由于需要一些特殊谱段估计水汽和气溶胶参数,此类方法多用于高光谱图像[9]。而光学图像波段较少,如GF-2卫星,除全色图像外,仅有4个谱段,无法从图中准确估计大气参数。且此类方法需要人工经验来选取合适的大气模型,也不适用于海量图像的自动化校正。
综上可以看出,目前已有的方法可以对单幅图像进行很好的色彩校正,但无法完成海量遥感图像的自动化色彩校正。近年来,机器学习的方法在计算机视觉领域取得了很多突破性的成果,在ImageNet[10]目标识别问题上,基于卷积神经网络——CNN(convolutional neural networks)的模型已经取得目前最好的结果,从2012年的AlexNet[11]到VGG[12],再到ResNet[13],网络结构还在不断被改进,分类的准确率也越来越高。现在已经有很多研究将机器学习的方法应用到遥感领域当中[14],目前大部分相关工作集中在目标检测与识别[15]和图像分类[16]等应用问题,但也有一些研究成功地将机器学习应用于遥感图像处理当中,例如2009年Lary等[17]利用机器学习的方法对MODIS大气气溶胶光学厚度进行偏置校正,2015年Ali等[18]总结机器学习方法在生物量和土壤湿度反演方面的应用,其结果均优于传统的方法,机器学习也给遥感图像色彩校正问题提供了新的解决思路。
本文提出基于稠密卷积神经网络——DCN(dense convolutional network)的方法,可以实现对海量不同大气条件下遥感图像的自动色彩校正。该方法通过直接预测每个通道的颜色校正系数K,实现对图像的颜色校正。此方法不依赖于人工经验和对场景的先验知识,模型训练完后,即可对全新的图像进行快速的色彩校正,且此方法不受限于输入图像的大小。
1 问题建模 1.1 大气模型色彩校正的目标是获得与地表真实颜色接近的遥感图像,可以认为RGB这3个波段地表反射率的颜色为真实颜色,若能准确地进行大气校正,就能获得颜色真实的图像。令卫星传感器获取到的辐亮度值为Ra,地表的反射率值为Re。根据FLAASH大气校正中的模型,对于一个像素点,每个波段上传感器接收到的辐亮度值Ra与地表的反射率Re有如下关系
| $ {R_{\rm{a}}} = \frac{{A{R_{\rm{e}}}}}{{1 - S{R_0}}} + \frac{{B{R_0}}}{{1 - S{R_0}}} + {R_{\rm{L}}}, $ | (1) |
式中:A, B, S, RL均为在一幅图像中随波段变化的量,在不同的空间位置上不变,由各项传感器参数和大气条件决定;R0为像素点周围的反射率均值,通常取1 km的量级,对于高分辨率光学图像来说,如分辨率为4 m的GF-2,为250×250的像素范围,在图像内变化缓慢,故也可近似为一个空间不变量。在这些条件下,上式退化为一个线性关系:
| $ \begin{array}{l} {R_{\rm{e}}} = K({R_{\rm{a}}} - L), \\ K = \frac{{1 - S{R_0}}}{A}, \\ L = \frac{{B{R_0}}}{{1 - S{R_0}}} + {R_{\rm{L}}}. \end{array} $ | (2) |
式中:L为图像中反射率为零的地物处的辐亮度值; K为颜色校正系数,主要由大气的参数决定。由快速大气校正[19]中使用的假设,图像中各波段最暗的地物点可以近似认为反射率为零,对于RGB 3个波段,可分别估计出图中的L值,故颜色校正取决于对K的估计。
1.2 评价标准RGB这3个通道的K值对应一个2维的颜色空间,即色相和饱和度。要得到颜色准确的图像,则需保证3维K向量K的方向保持准确,即预测出的向量K与真值向量K*方向保持一致,这两个向量的夹角即为色偏角[20](color angular error)θ,表达式如下
| $ \theta = \frac{{180}}{\pi }\arccos ({\mathit{\boldsymbol{K}}} \cdot {{\mathit{\boldsymbol{K}}}^*})0. $ | (3) |
计算机视觉领域[21]通常也使用θ作为颜色校正的标准。对于同一区域的已有图像和真值图像,直接使用最小二乘法计算两图的拟合系数K,公式如下
| $ {\mathit{\boldsymbol{K}}} = \frac{{n\sum {({{\mathit{\boldsymbol{x}}}_i}{{\mathit{\boldsymbol{y}}}_i}) - (\sum {{{\mathit{\boldsymbol{x}}}_i}\sum {{{\mathit{\boldsymbol{y}}}_i}} } )} }}{{n\sum {{\mathit{\boldsymbol{x}}}_i^2 - \sum {{{\mathit{\boldsymbol{x}}}_i}\sum {{{\mathit{\boldsymbol{x}}}_i}} } } }} $ | (4) |
式中:xi和yi分别为已有图像与真值图像的矩阵。计算K向量与标准向量(1, 1, 1)的夹角即为此图像的色偏角θ。
2 模型结构本文使用两个模型进行颜色校正,第1个为传统的CNN模型,第2个为DCN模型。
2.1 CNN模型AlexNet是2012年ImageNet目标识别比赛中的冠军队伍设计的经典CNN结构,其中用到的很多结构是后来众多改进网络的基础。AlexNet的前5个卷积层[11](Conv)及其辅助结构用于从图中提取空间纹理特征,并逐层向上转化为复杂的高级特征。第5层后则为3个全连接层(FC),使用前面提取的特征来获取高层语义特征,最终完成图像分类。
在AlexNet中,每个卷积层后都会接上一组激活层[11](ReLU)和归一化层[11](LRN)。激活层的作用是为网络产生非线性连接,从而使网络可以学习到复杂的非线性函数。如常用的ReLU激活层,其激活函数为:
| $ f(x) = \left\{ \begin{array}{l} 0, \;\;\;\;x < 0\\ x, \;\;\;\;x \ge 0 \end{array} \right.. $ | (5) |
x为输入值,这个函数在后来的神经网络中被广泛使用。归一化层全称为局部响应归一化层,目的是实现类似生物神经系统的侧抑制机制,使得响应较大的网络节点在附近相对更大,从而提升网络的泛化能力,后来的网络常用批归一化层[11](Batch Normalization)来代替这一层。当需要逐层减小输出特征的空间大小时,CNN会加入池化层[11](Pooling),AlexNet中在第1、第2和第5个卷积层后使用最大值池化层(Max Pooling),使得输入的227×227图像,经过5层后变成6×6的特征矩阵,将其拉伸为一维向量后即可接上全连接层来学习上层语义特征。全连接层通常还与随机丢弃层(Dropout)结合使用,该层在训练时会以一定的概率随机丢弃部分输入网络节点,从而有效地抑制过拟合的发生。
本文的CNN结构使用AlexNet的前5个卷积层及其激活层、归一化层和池化层,在此基础上增加1个卷积层和2个全连接层。
2.2 DCN模型全卷积神经网络(FCN)[22]是2015年由Chen S等人提出的模型,在图像语义分割中取得了目前最优的结果。传统的CNN会在卷积层结束后,接上全连接层来学习上层语义信息,而FCN则全部使用卷积层,没有全连接层,因此被称作全卷积。使用卷积层代替全连接层有很多好处,首先卷积层在空间上共享参数,参数数量比全连接层少很多,使得占用空间少,且不易过拟合,具有更好的泛化能力。FCN可以在输出层之前加上一个反卷积层,从而使输出层的大小与输入层相同,构成一个端到端的模型。而且由于全是卷积层,模型可以使用在不同大小的图像上,不用修改参数。
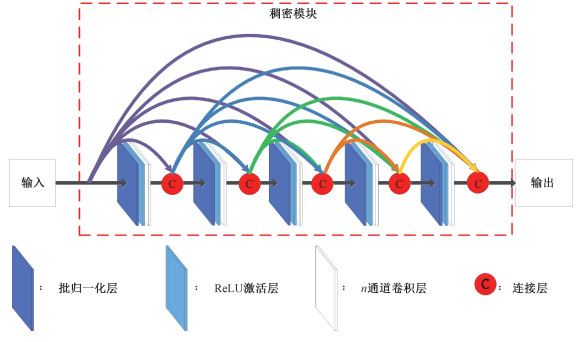
稠密连接的卷积神经网络(DenseNet)[23]是2017年Huang等提出的网络结构,在多个图像分类数据集上都取得了目前最优的结果。此前使用的网络,如AlexNet的卷积层往往特征维数很大,这一网络的思想是将多个特征维数很小的卷积层进行稠密连接,如图 2所示,前面所有卷积层的输出连在一起,作为后一个卷积层的输入,这样仅使用n层,就能得到n(n+1)/2个连接,从而用更少的参数拟合更复杂的函数。一组这样的卷积层被称为一个稠密模块(Dense Block),每个卷积层的特征维数被称为增长率(Growth Rate)。在这些模块间,有一个卷积核长宽为1的卷积层和一个核长宽和步长都为2的均值池化层(Average Pooling)。
|
Download:
|
| 图 2 含5个卷积层的稠密模块结构图 Fig. 2 The dense block with 5 convolutional layers | |
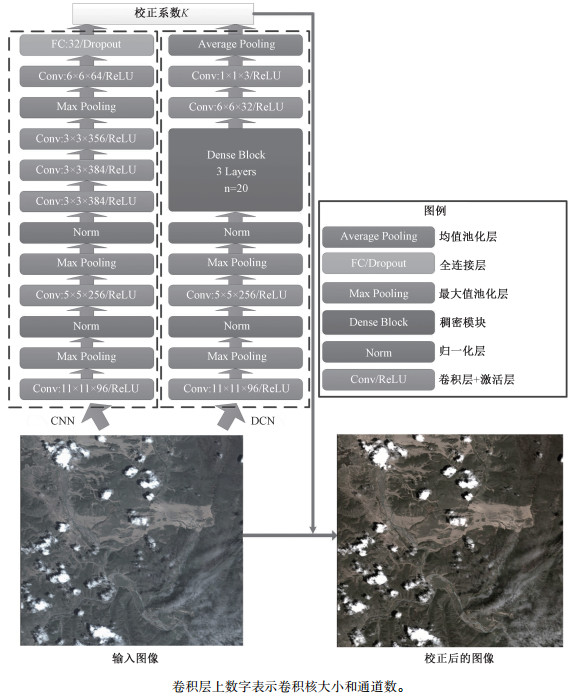
本文同时借鉴FCN的全卷积思想和DenseNet的稠密模块。DCN结构的前2层基于AlexNet的前2个卷积层,然后接上1个稠密模块,其中包含3个卷积层,增长率为20,卷积核为3×3,模块的输出再接上2个卷积层和全局均值池化层直接得到最终的3通道K值,图 3给出本文采用的DCN和CNN模型的结构及其具体参数,除第一个卷积层步长为4外,其他卷积层步长皆为1。由于没有全连接层,且最后用的是全局均值池化层,即对前一层的输出结果取空间上的平均值,故这一结构无需指定输入图像的大小。AlexNet的输入被限制为227×227,而DCN结构则可以使用较大的图像,本文使用1 280×1 440的图像。本应用需要从场景中预测颜色系数向量K,场景越大,包含的信息越丰富,就有利于产生更好的预测结果,这一改进对于其他基于场景的应用同样适用。除此之外,稠密模块能使用较少的卷积层数实现大量的连接,从而用较少的参数拟合复杂的函数关系,在本实验中,DCN的参数比传统CNN要少得多,在训练过程中可以更好地避免过拟合,而且训练速度也更快,这些优势非常适合海量遥感图像的处理。
|
Download:
|
| 图 3 本文的CNN和DCN模型结构 Fig. 3 CNN and DCN models used in this work | |
本文使用的数据集来源于GF2卫星多光谱遥感图像,其参数如表 1所示。实验中使用空间分辨率为4 m的3个波段:Band2、Band3、Band4,分别对应蓝(B)、绿(G)、红(R)3个波段。原始图像为未校正图像,作为实验时的输入。实验中根据实际地物颜色,对其中质量较好的图像进行人工校正,校正后的图像作为标准图像。用校正后的图像和原始图像计算得到校正系数向量K*作为训练时的真值,每一幅切片均对应一个3通道的K*值。
|
|
表 1 实验中GF2数据参数 Table 1 Parameters of GF2 data |
实验中总共裁剪出无重叠区域的3 000幅切片,大小为1 280×1 440,训练时随机选取70%作为训练集,剩下的30%则用于测试,测试图像与训练图像来自不同的区域,且使用随机颜色拉伸,保证每幅图的偏色系数各不相同。
为了抑制训练时的过拟合,实验使用数据扩展,对训练集的图像进行随机水平或垂直翻转。
3.3 训练参数实验中使用Tensorflow深度学习框架作为平台,训练时采用Adam(Adaptive Moment Estimation)优化器进行训练,初始学习率为0.000 1,分别在训练到20、35和50个样本周期(Epoch)时将学习率调低10倍。学习前对网络参数进行随机初始化,CNN的前5层和DCN的前2层使用AlexNet的预训练参数进行初始化。CNN和DCN均采用色偏角作为损失函数(Loss)。稠密模块的Dropout保留概率为0.8,全连接层的Dropout保留概率为0.5。
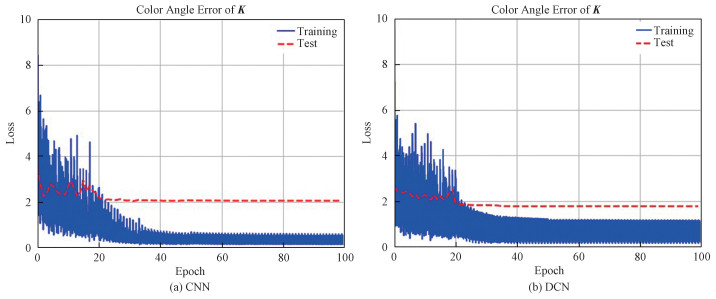
4 实验结果在tensorflow平台上分别实现图 3中CNN和DCN的模型结构,使用校正系数向量K与真值K*的色偏角作为损失函数进行训练,训练集每一步的损失函数值和测试集每个Epoch(数据集周期)的平均损失函数随训练步数的变化如图 4所示,可以看到DCN比CNN更快地将色偏角收敛到2.2以下,且最终收敛值也较低,而CNN则过拟合现象严重,训练集的色偏角远小于测试集,这也反映了使用卷积层代替全连接层的有效性。
|
Download:
|
| 图 4 训练集与测试集的损失函数随步数的变化 Fig. 4 Loss functions of the training and test data sets | |
由于测试集中各图像本身的原始颜色失真情况有所不同,色偏角均值不能完全反映校正效果,本文统计了测试集结果的色偏角均值、中值、最优25%和最差25%,如表 2所示。可以看到DCN的结果明显优于传统CNN的结果。
|
|
表 2 测试集的色偏角误差统计量 Table 2 The mean, median, best 25%, and worst 25% errors of the test set |
可以看到DCN方法的结果在均值、中值、最优25%和最差25%上均优于传统CNN方法,且相比于输入图像有巨大提高。使用预测得到的色彩校正系数对原始图像进行色彩校正,本文选取一些不同色彩失真情况下的图像,比较不同方法的校正结果,如图 5所示。可以看到,DCN的结果略优于CNN,这两种方法的结果与参考真值图像基本保持一致。而基于概率统计的方法——零阶统计方法则很不稳定,颜色校正软件,即Photoshop中的自动色彩校正功能,得到的结果也同样与真值图像相差较大,虽然这些处理结果在统计上达到了白平衡,但实际地物的颜色分布并非如此。

|
Download:
|
| 图 5 不同方法的校正结果比较 Fig. 5 The color correction results using different methods | |
实验中使用的图像虽然尺寸很大,为1 280×1 440×3,然而进行预测耗时并不长。DCN模型在单个NVIDIA® GeForce® GTX 1080图形处理单元上,一个Batch的5幅图像训练时间为1.3 s,而使用已经训练好的模型对新的图像进行校正,则每幅图仅需0.11 s,运算速度已经达到大规模处理的要求。模型训练完成后,不再需要人工经验和对场景的先验知识,可以在大规模实时处理系统中进行自动化的色彩校正。
5 总结本文提出的DCN模型可以自动化地预测输入图像的色彩偏差,从而进行颜色校正,不需要人工经验以及对场景的先验知识,且校正结果优于传统的CNN方法,适合于在大规模实时处理系统中进行色彩校正。
由于使用机器学习的方法,训练集的场景分布和标注精度会影响到最终结果,随着遥感数据的不断积累,标注精度的不断提高,本文提出的方法将会取得更好的校正结果。
| [1] |
Wu J, Wang D, Bauer M E. Image-based atmospheric correction of QuickBird imagery of Minnesota cropland[J]. Remote Sensing of Environment, 2005, 99(3): 315-325. DOI:10.1016/j.rse.2005.09.006 |
| [2] |
Fecker U, Barkowsky M, Kaup A. Histogram-based prefiltering for luminance and chrominance compensation of multiview video[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2008, 18(9): 1258-1267. |
| [3] |
Kim S J, Pollefeys M. Robust radiometric calibration and vignetting correction[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 30(4): 562-576. |
| [4] |
Buchsbaum G. A spatial processor model for object colour perception[J]. Journal of the Franklin Institute, 1980, 310(1): 1-26. DOI:10.1016/0016-0032(80)90058-7 |
| [5] |
Van d W J, Gevers T, Gijsenij A. Edge-based color constancy[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2007, 16(9): 2207-2214. DOI:10.1109/TIP.2007.901808 |
| [6] |
Hirakawa K, Chakrabarti A, Zickler T. Color constancy with spatio-spectral statistics[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 34(8): 1509-1519. |
| [7] |
Cheng D, Prasad D K, Brown M S. Illuminant estimation for color constancy:why spatial-domain methods work and the role of the color distribution[J]. Journal of the Optical Society of America A Optics Image Science & Vision, 2014, 31(5): 1049. |
| [8] |
Perkins T, Adlergolden S M, Berk A, et al. Speed and accuracy improvements in FLAASH atmospheric correction of hyperspectral imagery[J]. Optical Engineering, 2012, 51(11): 1707. |
| [9] |
Gao B C, Montes M J, Davis C O, et al. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean[J]. Remote Sensing of Environment, 2009, 113(9): S17-S24. |
| [10] |
Russakovsky O, Deng J, Su H, et al. ImageNet large scale visual recognition challenge[J]. International Journal of Computer Vision, 2015, 115(3): 211-252. DOI:10.1007/s11263-015-0816-y |
| [11] |
Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems. Curran Associates Inc. 2012: 1097-1105.
|
| [12] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. CoRR, 2014, arXiv:1409: 1556. |
| [13] |
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Computer Vision and Pattern Recognition. IEEE, 2016: 770-778.
|
| [14] |
Zhu X X, Tuia D, Mou L, et al. Deep learning in remote sensing:a comprehensive review and list of resources[J]. IEEE Geoscience & Remote Sensing Magazine, 2018, 5(4): 8-36. |
| [15] |
Chen S, Wang H, Xu F, et al. Target classification using the deep convolutional networks for SAR images[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(8): 4806-4817. |
| [16] |
Pasolli E, Melgani F, Tuia D, et al. SVM active learning approach for image classification using spatial information[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(4): 2217-2233. |
| [17] |
Lary D J, Remer L A, Macneill D, et al. Machine learning and bias correction of MODIS aerosol optical depth[J]. IEEE Geoscience & Remote Sensing Letters, 2009, 6(4): 694-698. |
| [18] |
Ali I, Greifeneder F, Stamenkovic J, et al. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data[J]. Remote Sensing, 2015, 7(12): 221-236. |
| [19] |
Gregor B, Adlergolden S M. Quick atmospheric correction code:algorithm description and recent upgrades[J]. Optical Engineering, 2012, 51(11): 1719. |
| [20] |
Barron J T. Convolutional color constancy[C]//IEEE International Conference on Computer Vision. IEEE, 2016: 379-387.
|
| [21] |
Barron J T, Tsai Y T. Fast Fourier color constancy[C]//Computer Vision and Pattern Recognition. IEEE, 2017: 6950-6958.
|
| [22] |
Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[C]//Computer Vision and Pattern Recognition. IEEE, 2015: 3431-3440.
|
| [23] |
Huang G, Liu Z, Weinberger K Q, et al. Densely connected convolutional networks[C]//Computer Vision and Pattern Recognition. IEEE, 2017: 2261-2269.
|
 2019, Vol. 36
2019, Vol. 36 


