人类的生产和生活都离不开能源，能源是社会和经济发展的重要支撑。世界各国科学家一直致力于对新能源的探索研究。可控核聚变是能量巨大、原材料取之不尽、干净、安全的新能源^[1]。限制器作为核聚变磁约束装置中至关重要的组成部分，核聚变装置限制器可以有效地屏蔽来自器壁的杂质，排出来自中心等离子体的粒子流和热流。液态金属可以较好地完成这一任务。液态金属具有导热性强、液相温度范围大、易于补充等特性，是未来聚变反应堆面向等离子体部件的主要备选材料之一。液态金属^[2]自由表面的多场耦合作用下的流动和传热规律是目前关注的重点。热毛细对流是一种与流体自由表面或界面相关的热对流，宏观上表现自由表面或界面温度分布不均匀而引起表面张力梯度驱动的流体流动^[3]。

导电流体通过磁场时将产生诱导电流，此诱导电流与磁场相互作用在流体中产生一个与流动方向相反的洛仑兹(Lorentz)体积力，即磁流体动力学MHD效应^[4]。磁场作用下的热毛细对流不同于一般流体的热毛细对流，除与温差、表面张力有关，还与磁场有关，是多场强耦合作用下的流动传热过程，因而对其进行深入研究具有重要的工程价值和科学意义。

近年来，许多国内外学者对于热毛细对流进行了较多研究。李炜等^[5]及Hossain等^[6]通过数值模拟的方法，对磁场作用下的双扩散液层热毛细对流进行研究，得到液层内部对流结构同磁场强度的变化规律。Kamotani等^[7]对方腔内硅油的自由表面受到热毛细对流及自然对流共同影响的形貌变化进行深入分析。Gupta等^[8]、Qin等^[9]及Jue和Ramaswamy^[10]对流动结构的自由表面热毛细流动的传热影响进行研究，通过设计物理模型、考虑两不互溶流体自由表面以及交界面的形变，对传热效果进行数值模拟。随着温度梯度的增加，交界面处的流动更加剧烈，并且等温线向两端倾斜的趋势更加明显。

虽然已有研究人员对于热毛细流动进行了研究，但大部分停留在二维数值模拟方面，系统的实验研究和热毛细对流自由表面形貌特征研究较少，对于液态金属自由表面的热毛细流动以及强磁场对于三维实际工况的影响等方面目前未见报道，这是本文开展实验研究的创新点。本文首先采用可视化的透明碳酸钾溶液为工质进行导电流体热毛细流动研究实验，在此基础上加深对液态金属自由表面流动情况的理解后，研究碳酸钾溶液和镓铟锡液态金属合金溶液在不同磁场强度和温度梯度下的热毛细对流流动和传热规律。

1 实验装置

在聚变堆中，在强磁场的约束下，反应堆内部是一个电场、磁场、带电和中性粒子高速运动的复杂系统。在聚变堆超强磁场的环境中，面向等离子体部件的液态金属不仅受到强磁场的作用，而且受到高温等离子体的辐照，二者作用在液态金属上会产生强磁场作用下的热毛细对流现象。强磁场作用下的热毛细对流会影响液态金属自由表面流速分布，产生不同于无磁场下的流动设计参数，威胁聚变堆面向等离子体部件的安全和聚变堆运行的稳定性，因此深入研究该热毛细对流的特性和机理具有十分重要的意义。

分析该过程可以获得聚变堆中强磁场对液态金属自由表面形态的影响规律，进一步研究液态金属自由表面热毛细对流自由表面的传热过程。

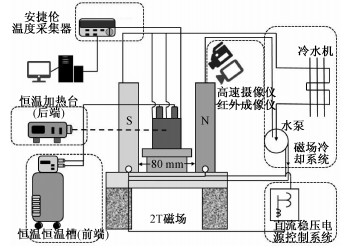
为模拟这一过程研究液态金属热毛细对流现象，本文设计完成了导电流体在矩形液池内的热毛细对流实验系统，如图 1所示。

矩形容器的水平横截面为60 mm×60 mm，两个相对的侧面是聚碳酸酯板(俗称PC板，热导率为0.2 W/(m·K))，壁面厚度为5 mm。PC板的透明度高，便于对实验内部流体进行观察；而且可以耐受较高的温度。PC板外侧包裹一层5 mm厚的隔热海绵用于隔热。在实验段两侧，左面是紫铜导热板，右面是中空紫铜制成的水冷板。容器内部盛有碳酸钾薄层液体，在两侧高低温的作用下，液体表面产生温度梯度。液体表面的温度通过热电偶进行测量。热电偶采用电极材料为铬镍-硅镍的K型热电偶。高温端采用高精度恒温加热器进行温度控制加热，低温端通过低温恒温槽对其进行温度控制冷却，使得两端可以保持恒定的高低温。

实验中，液层两侧的温差将逐渐增大观察实验现象。由于碳粉的密度小于水溶液，可以较容易地悬浮在液体表面，所以液体表面流动的示踪粒子采用直径为15~20 μm的碳粉颗粒，碳粉具有较强的液面跟随性，可以较好地反应液体表面的流动情况。通过高速摄像机对碳粉运动情况进行拍摄，以两张图片同一颗粒的移动距离除以两张图片的曝光时间间隔，所获得的速度即为液体自由表面的瞬时速度。

实验开始首先打开安捷伦34970A进行温度实时监控与测量，在实验段中注入5 mm厚度的液态工质。本文中引入无量纲参数邦德数$Bo = \frac{{\Delta \rho g{L^2}}}{\sigma }$，表征重力(浮力)比上表面张力(热毛细力)。

当邦德数小于1时，热毛细作用起主导作用；当邦德数大于1时，浮力起主导作用。此文中Bo=0.020 7，如Kuhlmann和Albensoeder^[11]所述，浮力影响可以近似忽略。并且文中引入瞬时功的概念：$B = \frac{{Gr}}{{{D_{{\rm{kin}}}}}}v\theta $，其中${{D}_{\text{kin}}}=\iiint{{{\omega }^{2}}\text{d}V}$，θ表示温度，那么由浮力产生的能量$\iiint{B\text{d}V}$如果足够小或者为负数，可以忽略浮力影响。在目前宽深比Г=12的情况下，浮力产生的能量为负值，因此目前实验系统浮力可忽略。

实验中采用质量分数为5%的碳酸钾溶液。在此引入无量纲参数$Ma=-\frac{\text{d}\gamma }{\text{d}T}\frac{L\Delta T}{\mu \alpha }$，它表征表面张力与黏滞力之比。通过改变实验台两端温差，使得Ma数分别为6.97×10⁵, 1.39×10⁶, 2.09×10⁶, 2.79×10⁶, 3.48×10⁶。用高速摄像机拍摄下碳粉颗粒循环图像，对颗粒实时跟踪拍摄，同时用红外线成像仪对液体自由表面温度分布进行拍摄测量，并测量和记录液面的温度分布。

2 导电流体热毛细对流实验结果分析 2.1 无磁场情况下表面流动规律

实验介质是质量分数为5%的碳酸钾溶液，2003年国际空间站(ISS)实验中水薄膜自由表面的流动方向和常规的流动方向相反，方向是从冷端流向热端^[12]。本实验表面流动矢量图如图 2(a)所示，主流流动方向和ISS实验方向相符。主流流动从冷却面流向加热面。图 2(b)为自由表面俯视拍摄图，表面黑色颗粒是本实验的示踪粒子碳粉颗粒。由于液面较薄，主流区域所占面积较大，在绝热壁面附近存在两个所占区域较小的回流。该回流流动速度较大，方向为从热到冷。如此反复流动，表面会形成循环流动结构。

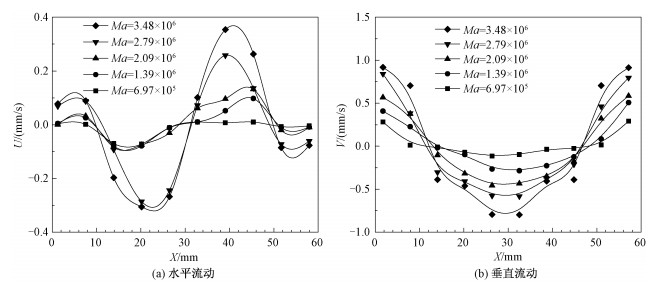
速度所取位置为自由表面距离加热面5 mm处，并且垂直于热流梯度的截线上的流速。流速变化如图 3所示。随着Ma数的增大，液体冷热端温差越大，表面张力梯度越大，液体自由表面流速也随之上升。

2.2 磁场情况下表面流动规律

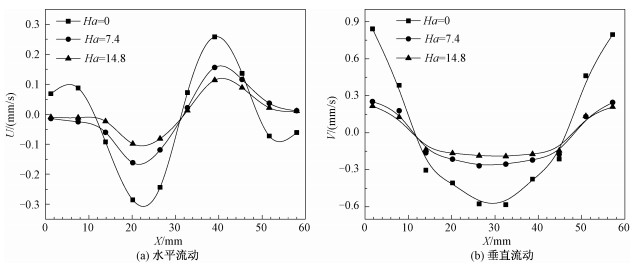
为进一步研究磁场对自由表面的热毛细对流流动与换热的影响规律，本文将热毛细对流实验装置放入磁场中观察表面速度以及换热变化规律。磁场方向垂直于主热流梯度方向。由于小温差和小磁场情况下速度以及传热变化不明显难以测量所以本文给出Ma=2.79×10⁶情况下不同磁场表面的流动速度以及速度变化情况，如图 4所示。

在此处引入哈德曼数这一无量纲参数$Ha=\mathit{\boldsymbol{B}}L\sqrt{\frac{{{\sigma }_{m}}}{\mu }}$，它表征电磁效应与黏性效应之比。流场和磁场之间的耦合是通过诱导电流和洛伦兹力这两个概念实现。导电流体在磁场中运动，与磁场相互作用产生诱导电流J，诱导电流和磁场相互作用在流体内部产生洛伦兹力F。

本文所用磁场方向为水平磁场，磁场方向垂直于主流方向，得到生成的洛伦兹力平行于流体流动方向，且与流动方向相反，从而对流体的流动产生抑制作用。流速越大，洛伦兹力越大，抑制效果越强。如图 4所示，变化磁场情况下，液层自由表面速度明显减小。随着Ha数增大，速度总的变化趋势不变，但速度绝对值明显减小，这表明磁场能够有效抑制热毛细对流。

2.3 磁场作用下换热分析

本实验通过测量GaInSn和K₂CO₃溶液实验系统冷端紫铜板内外两侧的温差计算热流量Q。即Q=λ_copperA(T_out-T_in)/L，在此引入无量纲参数Nu，它是表征对流换热程度的无量纲参数。

$ Nu=\frac{hL\prime }{{{\lambda }_{\text{GaInSn}}}}=\frac{Q}{A({{T}_{\text{h}}}-{{T}_{\text{c}}})}\frac{L\prime }{{{\lambda }_{\text{GaInSn}}}}, $

(1)

$ Nu=\frac{hL\prime }{{{\lambda }_{{{\text{H}}_{\text{2}}}\text{O}}}}=\frac{Q}{A({{T}_{\text{h}}}-{{T}_{\text{c}}})}\frac{L\prime }{{{\lambda }_{{{\text{H}}_{\text{2}}}\text{O}}}}. $

(2)

式中:A代表铜板与介质接触表面积；T_in表示水冷板内侧的平均温度；T_out代表水冷板外侧与介质接触的面上的平均温度；L为特征长度(文中所取特征长度为冷热两端距离60 mm)。λ_copper, λ_GaInSn, λ_H2O分别代表铜，GaInSn和K₂CO₃溶液的导热系数。

实验系统参数如表 1^[13]所示。本实验将GaInSn和K₂CO₃溶液实验系统放置于磁场内部，对整个实验系统的换热情况进行分析。

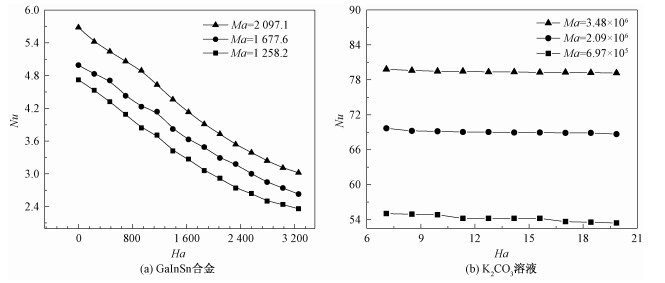
如图 5所示在磁场垂直于热流梯度方向时，磁场明显对流体的换热起到阻碍作用，随着磁场的增大抑制效果也愈加明显。

磁场对GaInSn的换热抑制比K₂CO₃溶液更加明显是因为GaInSn合金的电导率要远大于K₂CO₃溶液的电导率，在磁场中受到热梯度驱动的流动所产生的洛伦兹力更大，洛伦兹力的产生将有效地阻碍表面张力驱动流。可以看出温差越大，所驱动的表面流动速度越大，从而切割磁感线产生的洛伦兹力越大，Nu随Ha增加下降得越快。同时下降的斜率越来越趋近于平缓，说明在磁场足够强时，洛伦兹力、表面张力和重力趋于平衡，磁场产生的抑制效果也将不再发生明显变化。

同时，K₂CO₃溶液的Nu也随Ha增大而逐渐减小，但由于K₂CO₃溶液的电导率较小，所以产生的洛伦兹力要明显小于GaInSn，所以增大磁场所产生的抑制效果不如GaInSn那么明显，但仍可以看出变化趋势也是逐渐趋于平缓。

为了进一步对磁场中液态金属自由表面热毛细流动系统的换热情况与磁场之间的关系进行无量纲分析，对于无量纲参数努塞尔数Nu、哈德曼数Ha以及Ma的关系进行函数拟合。拟合的公式为

$ Nu=0.163\times M{{a}^{0.47}}{{\text{e}}^{-2.13\times 10}}^{^{-4}Ha}. $

(3)

拟合曲线中，3种不同Ma的函数与所得的拟合曲线平均误差小于5%，相关系数达0.99，由此可以得到无量纲参数努塞尔数和哈德曼数之间的函数关系。可以得到Nu随Ma的变化呈幂函数关系，与哈德曼数的变化呈指数函数关系。磁场增大会抑制换热效果，温差增加会增大换热效果，得到的结果与我们预期相符。

3 结论

热毛细对流是由于自由表面温度分布不均匀所引起的表面张力梯度驱动的流体流动。在聚变堆中，由于大温差和大热源的存在，液态金属的热毛细对流是一个重要的研究内容，在磁场作用下热毛细对流不同于一般流体的热毛细对流。

本文以流体自由表面热毛细对流为研究对象，研究自由表面水平温差梯度驱动下的热毛细对流产生条件、演化机理及其磁场主动控制的规律。研究内容以及获得的研究结果如下：

采用图像分析法对矩形腔体内流体自由表面热毛细对流进行实验研究。自由表面先因为存在温差，导致主流方向存在表面张力梯度，从而表面存在由冷却面流向加热面的主流流动。又因为液面较薄，自由表面需要补充不断流出的流体工质，因而绝热壁面两侧存在从加热面流向冷却面的补充流，自由表面会形成两个环形流动。并且两侧温差越大，自由表面表面张力梯度越大，流动速度也越大。

在加入磁场的情况下，磁场方向与主热流梯度方向相垂直。磁场的加入，使得导电流体受到洛伦兹力的作用，抑制自由表面流体的流动, 从而减弱热毛细流动，减弱流体的对流换热，使得换热效果受到削弱。并且磁场强度越强，对于热毛细流动的抑制效果越强。