2. 新疆大学机械工程学院, 乌鲁木齐 830047
2. School of Mechanical Engineering, Xinjiang University, Urumqi 830047, China
转子轴承系统作为旋转机械的核心部件,在工业领域发挥着无可替代的作用。随着旋转机械向高速、重载和自动化方向发展,对转子轴承系统的安全性和稳定性提出了更高的要求。传统的转子轴承在设计或使用上都会存在局限性,因为理论上固定瓦轴承转子系统是基于某种特定工作状况进行设计的,然而在实际生产过程中,其工作状况可能有所变化,转子轴承系统的初始设计状态与实际工作状态可能不同:如发电机组会根据用电量的不同,调整其工作载荷;内燃机、压缩机等工作转速可能随时发生变化,对于某一特定参数的固定瓦轴承转子系统来说无法适应这种时变的工作状态,也不能根据轴承的实际工作要求调整其工作参数。由此可能会造成轴承的磨损、轴系的振动,缩短轴承的使用寿命,影响转子轴承系统的稳定性,严重的甚至会出现抱轴、烧瓦、油膜失稳等安全事故。而这些核心设备一旦损坏,将造成巨大的经济损失。
对时变工况下转子轴承系统的动力学特性的研究,国内外学者投入其中并在理论和实验研究方面取得了一系列成果。Lee等[1]用状态空间Newmark有限元瞬态响应分析方法,研究冲击激励作用下转子轴承系统的响应,并进行试验对比验证;Han和Chu[2]研究在周期性摆角运动下,对柔性转子轴承系统运行参数稳定性的影响;刘树鹏[3]研究舰船纵横倾作用下转子轴承系统动力学特性,得到摇摆参数对系统动力学特性的影响。Dhawan和Verma[4]基于椭圆轴承研究其转子的动力学特征,并指出在牛顿流体润滑条件下椭圆轴承拥有更好的使用性能。Schweizer[5-7]研究润滑油温度、供油压力和不平衡量对涡轮增压器转子系统稳定性的影响,研究结果表明适当的偏心会提高系统的失稳转速,另外不平衡量引起的同步振动和内外油膜涡动在转速达到一定范围相互转化,系统振幅大幅增加。Prabhakaran等[8]研究在供油量偏少的情况下,椭圆轴承转子的静态和动态特性。Rahmatabadi等[9]在此的基础上,分析力偶流体对椭圆轴承动特性的影响。陈红霞等[10]分析偏载条件下椭圆轴承的动静特性。张宏献等[11]研究椭圆度对椭圆滑动轴承稳定性的影响。目前学术界对不同工况下椭圆轴承转子系统的动力学特性有了初步的认识,但是针对利用轴承控制技术维持转子系统稳定的研究工作非常少,还存在很多问题。因此,为提高转子轴承系统在时变工况下的稳定性和安全性,很有必要针对参数可调椭圆瓦轴承支撑的转子系统的动力学特性进行深入分析和研究。
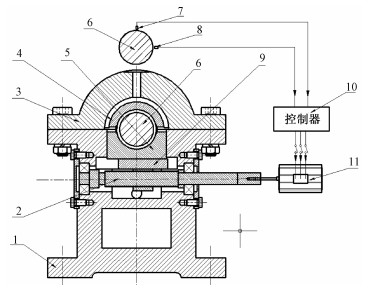
为适应时变工况,维持转子轴承系统在不同工作状态下的稳定性,经研究提出一种参数可调椭圆轴承转子系统装置,如图 1所示。该装置包括几何尺寸可调的滑动轴承支撑结构和检测控制系统两部分。其中几何尺寸可调的滑动轴承支撑结构分为滑动轴承和支撑结构,支撑分为支撑座1和支撑盖3,二者相对安装;轴承安装在支撑结构内部,轴承又分为上下两瓦,二者相对安装,上瓦4固定,下瓦5可以在支撑结构内部上下滑动。在检测控制系统中,位移传感器7、8安装在轴承支撑轴颈处,并与状态监测控制器相连,控制器可以控制伺服电机11转动,伺服电机11带动丝杠2转动,丝杠2带动斜铁9移动,斜铁9的移动使轴承下瓦上下滑动。当转子6的运行工况发生变化时,通过位移传感器检测转子6的运行信号,然后将信号传递给智能控制器10,智能控制器10根据转子信号做出判断,控制伺服电机11转动使下瓦5上下滑动,从而改变轴承的几何尺寸来调节转子的运转状况。该装置可以实时监测转子的运行状况,通过伺服电机的转动调节轴承下瓦的上下滑动的距离,对变化的工况做出判断,调整轴承的几何尺寸,使转子轴承系统稳定安全运行。
|
Download:
|
| 1支撑座;2丝杠;3支撑座上盖;4轴承上瓦;5轴承下瓦;6转子;7和8高精度位移传感器;9斜铁;10控制器;11伺服电机。 图 1 一种参数可调椭圆轴承转子系统装置 Fig. 1 Structure of an adjustable elliptical bearing rotor system | |
在本装置中,当转子的工作状态发生变化,通过位移传感器采集信号,智能控制器对转子的振动信号进行分析,如果轴承的工作状态和设计的状态不同,或者转子的振动幅值过大时,控制器就会发出控制信号,控制伺服电机转动一定的角度,通过改变轴承的油膜间隙调整转子的工作状态。转子的工作状态在调整后将继续由传感器进行测量,若仍未达到工作要求,控制器将对轴承参数做进一步的修正,直至满足工作要求为止。参数可调转子轴承系统运用主动控制的方法对转子系统的工作状态进行调节,在一定程度上减少由于转速、载荷等变化的工况所造成的安全事故隐患。
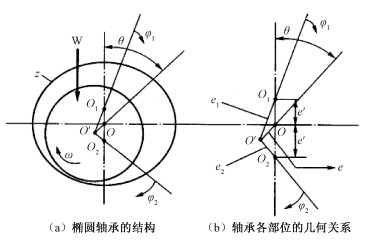
1 椭圆轴承的设计 1.1 椭圆轴承的几何关系“椭圆轴承”中的椭圆不是数学上定义的椭圆,它是由圆心不重合的两个圆弧组成的,如图 2所示。图中,O′为轴颈的轴心,O为椭圆轴承的几何中心,O1O2分别为轴瓦1、2的瓦中心,e为椭圆轴承的偏心距,θ为椭圆轴承的偏位角,e1、e2分别为轴瓦1、轴瓦2的偏心距,e′为预置偏心距。轴瓦1和轴瓦2的膜厚为:
| $ \begin{align} &{{h}_{1}}\approx C+{{e}_{1}}\text{cos}{{\varphi }_{1}}, \\ &{{h}_{2}}\approx C+{{e}_{2}}\text{cos}{{\varphi }_{2}}. \\ \end{align} $ |
|
Download:
|
| 图 2 椭圆轴承的结构和几何关系 Fig. 2 Structure and geometry relations of elliptical bearing | |
式中
| $ \begin{align} &{{e}_{1}}={{[{{e}^{2}}+{{\left( e\prime \right)}^{2}}+2ee\prime \text{cos}\theta]}^{\frac{1}{2}}}, \\ &{{e}_{2}}={{[{{e}^{2}}+{{\left( e\prime \right)}^{2}}-2ee\prime \text{cos}\theta]}^{\frac{1}{2}}}. \\ \end{align} $ |
各轴瓦最小润滑膜厚度
| $ \begin{align} &{{h}_{\text{1min}}}=C-{{e}_{1}}, \\ &{{h}_{\text{2min}}}=C-{{e}_{2}}. \\ \end{align} $ |
椭圆轴承的最小油膜厚度在两轴瓦最小润滑膜厚度中取较小的一个。
当轴颈中心与轴承几何中心重合时,椭圆轴承的半径间隙最大值(通常也称为侧隙)为Cmax=Cr(Cr=R-r);半径间隙最小值(通常也称顶隙)为Cmin=C-e′。
定义椭圆度δ为δ=e′/C,顶隙比为ψmin=Cmin/R,侧隙比为ψmax=C/R,则轴承的椭圆度为δ=1-ψmin/ψmax。
1.2 椭圆轴承椭圆度的设计轴承的设计是实验台设计过程中非常重要的一环。设计要求椭圆轴承的椭圆度能在尽可能大的范围内变化,本文涉及的下轴瓦可上下活动的距离为96 μm,如果轴瓦的上下运动全部用于轴承椭圆度的调节且轴承椭圆度在0.1~0.7之间变化,由于轴承顶隙的变化范围为96 μm,由以上条件列出如下3个方程:
| $ \begin{align} &1-\frac{{{C}_{\text{min}1}}}{{{C}_{\text{max}}}}=0.1, 1-\frac{{{C}_{\text{min}2}}}{{{C}_{\text{max}}}}=0.7, \\ &\ \ \ \ \ {{C}_{\text{min1}}}-{{C}_{\text{min}2}}=96. \\ \end{align} $ |
联立解得Cmax=160 μm,即加工时孔与轴的配合间隙为160 μm。
由上述方案,顶隙和侧隙分别为:
| $ {C_{{\rm{max}}}} = 160\;{\rm{ \mathsf{ μ} m}};{C_{{\rm{min}}}} = 48 \sim 144\;{\rm{ \mathsf{ μ} m}}. $ |
由轴承的椭圆度
根据前面的设计计算得到椭圆轴承的基本参数,对于轴承的其他参数,根据一般经验和实验台其他部件(如基座、轴等)进行初步确定。表 1为椭圆轴承的参数。
|
|
表 1 椭圆轴承的参数 Table 1 Parameters of elliptical bearing |
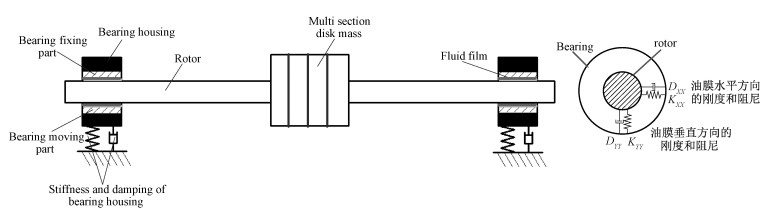
如图 3所示,首先建立转子轴承模型,在转子的两端安装参数可调椭圆轴承,中间安装质量盘;然后通过调节椭圆度,改变轴承的油膜间隙,研究不同椭圆度下转子轴承系统的动力学特性。转子轴承系统的参数如表 2。需要指出的是,模型采用转子自重作为静载荷计算转子轴承系统的动力学特性。
|
Download:
|
| 图 3 参数可调椭圆滑动轴承转子系统模型 Fig. 3 Model of an adjustable elliptical bearing rotor system | |
|
|
表 2 转子轴承系统参数 Table 2 Rotor-bearing system parameters |
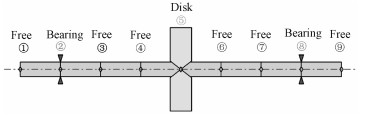
根据转子系统的结构参数(表 2),建立两端轴承支撑的转子系统有限元模型,有限元模型有8个梁单元,9个节点,18个自由度(如图 4所示)。轴承分布在第2和第8个节点,质量盘在第5个节点位置。当系统的椭圆度改变时,只需把相应椭圆度下的刚度和阻尼矩阵代入到轴承节点的矩阵中,然后建立对应动力学方程求解响应。
|
Download:
|
| 图 4 转子轴承系统有限元模型 Fig. 4 Finite element model of rotor-bearing system | |
转子轴承系统的动力学方程
| $ \mathit{\boldsymbol{M\ddot{q}}}+\mathit{\boldsymbol{C\dot{q}}}+\mathit{\boldsymbol{Kq}}=\mathit{\boldsymbol{F}}, $ |
位移响应计算公式
| $ \mathit{\boldsymbol{q}}={{[-{{{\mathit{\Omega}} }^{2}}\mathit{\boldsymbol{M}}+\text{j}{\mathit{\Omega}} \left( {\mathit{\Omega}} \mathit{\boldsymbol{G}}+\mathit{\boldsymbol{C}} \right)+\mathit{\boldsymbol{K}}]}^{-1}}{{\mathit{\Omega}}^{2}}\left\{ \frac{\frac{m\varepsilon {{\text{e}}^{\text{j}\delta }}}{-\text{j}m\varepsilon {{\text{e}}^{\text{j}\delta }}}}{\frac{\text{j}({{I}_{d}}-{{I}_{p}})\beta {{\text{e}}^{\text{j}\gamma }}}{({{I}_{d}}-{{I}_{p}})\beta {{\text{e}}^{\text{j}\gamma }}}} \right\}. $ |
式中:M为结构质量矩阵;C为阻尼矩阵;K为结构刚度矩阵;q为位移矩阵;F为载荷矩阵。阻尼矩阵C考虑陀螺效应和Rayleigh阻尼矩阵,Rayleigh阻尼矩阵为M和K的线性组合,即αM+βK,其中α和β是不依赖于频率的常数,它们与系统的阻尼系数和前两阶固有频率有关。F由不平衡力和重力组成。G为陀螺矩阵。m为转子的总质量,ε为偏心距,Ω为转子的角速度,δ为相位角,Id为转子的惯性矩,Ip为转子的极惯性矩,γ=Ip/Id。
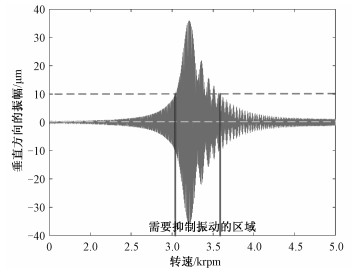
转子在临界转速附近的振动状态复杂,对转子系统的稳定性有很大的影响,所以很有必要研究转子转速越过临界转速时的动力学特性。图 5所示是圆轴承支撑时转子系统加速过程的振动响应,随着转速的增加转子的振幅增大,当转速达到临界转速(约3 200 rpm)附近时振幅急剧增加,这时转子系统存在安全隐患。为减小振动幅值,使转子系统安全稳定运行,可以在达到临界转速前调节油膜间隙,减小振幅。
|
Download:
|
| 图 5 转子加速过程的振幅响应 Fig. 5 Vibration response from rotor system during acceleration process | |
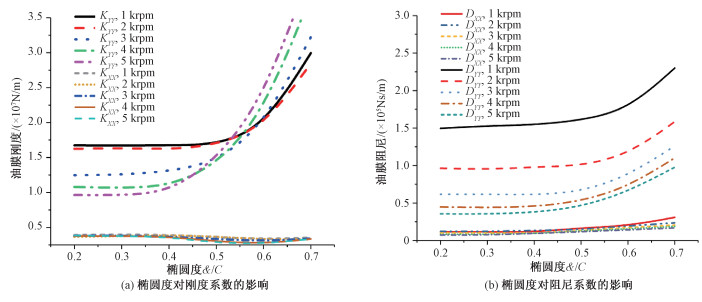
为减小经过临界转速时转子的振幅,需要研究不同椭圆度轴承的动力学特性。下面分别是对不同椭圆度下,通过求解非定常工况的雷诺方程得到轴承的静特性,用小扰动法来求解线性化的刚度和阻尼。根据第1节椭圆轴承的设计过程可以得到,当轴瓦向上移动0.2倍的半径间隙时对应的椭圆度为0.2,轴瓦向上移动0.7倍的半径间隙时对应的椭圆度为0.7,所以轴瓦的位移除以半径间隙(&/C),就是椭圆度的数值。图 6是利用西安交通大学润滑理论与轴承研究所研发的转子轴承系统动力学分析软件DLAP(dynamic lubrication analysis program)计算的数据绘制,该软件已经过多次验证,计算结果可靠[12-14]。图 6(a)是椭圆度对刚度系数的影响,图 6(b)是椭圆度对阻尼系数的影响。其中KXX代表水平方向的刚度,KYY代表垂直方向的刚度;DXX代表水平方向的阻尼,DYY代表垂直方向的阻尼。因为交叉刚度阻尼计算出来的数值很小,比垂直刚度阻尼小2个数量级,对动力学计算几乎不产生影响,所以忽略不计。
|
Download:
|
| 图 6 椭圆度对刚度和阻尼系数的影响 Fig. 6 Influence of ellipticity on stiffness and damping coefficient | |
由图 6发现轴承瓦的位移对动力学系数产生很大影响。转速在1 000~5 000 rpm范围内,当轴瓦移动0.7倍半径间隙时,垂直方向刚度几乎为初始值的2倍,水平方向刚度几乎不变;垂直方向阻尼增大为初始值的1.5倍,水平方向阻尼增大0.2倍。通过计算得到不同椭圆度下轴承刚度和阻尼的变化,为下面的动力学研究提供参考。
2.2 不同椭圆度下转子系统的动力学响应利用图 3所示参数可调椭圆轴承转子模型,研究不同椭圆度下转子系统的动力学响应。根据图 6轴承刚度阻尼随椭圆度的变化,把不同椭圆度的刚度和阻尼值分别代入到动力学方程中,利用Runge-Kutta变步长积分求解动力学方程,得到转子加速过程的动力学响应。
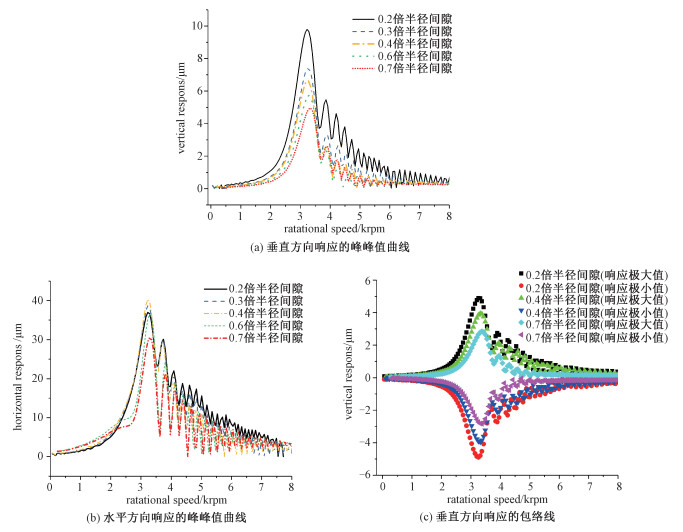
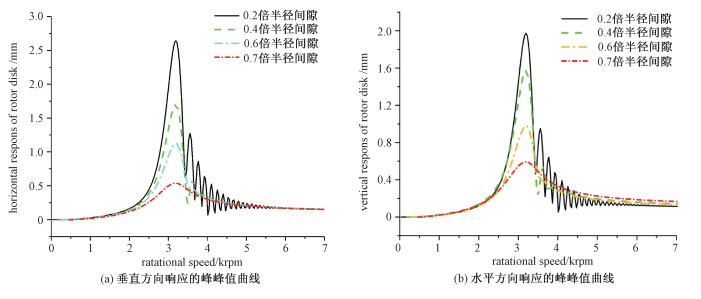
下面是转子以3 rad/s2的加速度越过临界转速,得到转子中间位置和轴承位置加速过程的振动响应。图 7, 图 8分别是在轴承位置和转子中间位置,不同椭圆度下的振动响应。
|
Download:
|
| 图 7 转子加速过程轴承支撑处轴颈的响应 Fig. 7 The response from the journal during acceleration process at different ellipticity values | |
|
Download:
|
| 图 8 转子加速过程质量盘处轴颈的响应 Fig. 8 The response from the rotor disk during acceleration process at different ellipticity values | |
由图 7加速过程转子响应的峰峰值曲线可以得出,转子加速到3 200 rpm左右时达到临界转速,这时转子的振幅最大,与图 5圆轴承支撑时转子系统加速过程的振动响应曲线一致。然后由不同椭圆度下计算的振幅峰峰值曲线可以发现,随着椭圆度的增大,转子经过临界转速的振幅减小。在垂直方向,椭圆度为0.1时,轴颈的振幅为11 μm;随着椭圆度的增加轴颈的振幅减小;当椭圆度为0.7时,振幅减小到5 μm。在水平方向椭圆度为0.1时,轴颈的振幅为40 μm;当椭圆度为0.7时,振幅减小到30 μm。轴瓦向上位移越大时,垂直方向抑制振动效果就越明显,这是由于轴瓦位移越大,油膜压力变化就越大,导致动力学系数变化越大。由于轴瓦是向上移动,垂直方向油膜间隙减小,油膜力变化明显,对轴颈的抑振作用可以达到70%以上,水平方向油膜间隙基本不变,所以抑振效果较小。
图 8为转子加速过程质量盘处轴颈的振动响应,由于质量盘安装在转子中间位置,并且转速在一阶临界转速范围,激发转子的第一节阵型,质量盘处轴颈振幅最大。从分析结果可以看出,当椭圆度为0.2时,垂直方向的振幅为2 mm,水平方向的振幅为2.7 mm;椭圆度为0.7时,垂直方向振幅为0.5 mm,水平方向的振幅为0.47 mm。说明通过调节椭圆度可以使转子垂直方向、水平方向的响应都明显减小,并且抑振程度基本相同,都达到70%以上。
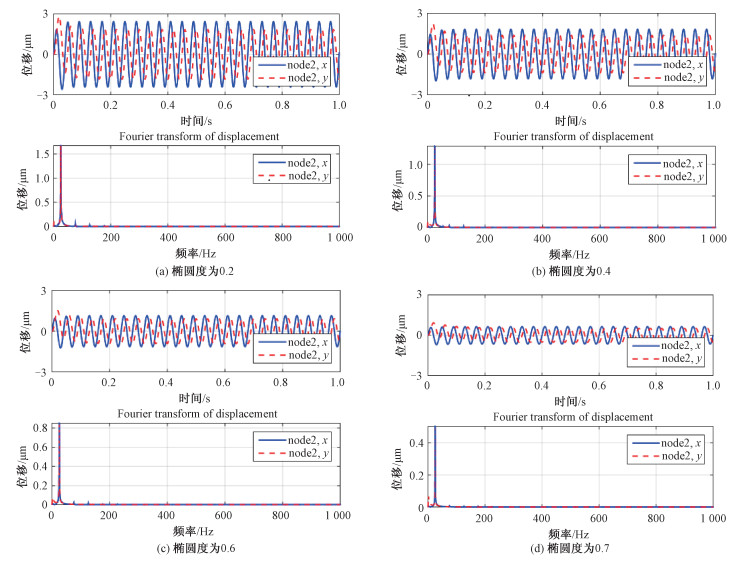
2.3 不同椭圆度下转子系统的瞬态动力学分析转速固定为2 000 rpm时,在不同椭圆度下对转子模型进行全瞬态动力学分析,得到轴承支撑处x,y方向的时域与频域响应,如图 9所示。
|
Download:
|
| 图 9 椭圆瓦轴承支撑转子的瞬态动力学响应 Fig. 9 Transient dynamic response from the rotor supported by elliptical bearing | |
通过图 9瞬态动力学分析结果,可以得到不同椭圆度下轴颈处的时域和频域响应。以轴承支撑处轴颈的振动为衡量标准,椭圆度为0.2时轴颈最大振幅约为6 μm;椭圆度为0.7时最大振幅约为1 μm; 随着椭圆度的增大,轴颈的振动明显减小,说明调节椭圆度可以有效地抑制振动。并且在不同椭圆度下,轴颈振动都较小,轴颈最大振幅6 μm远小于间隙圆半径40 μm,说明转子轴承系统可以安全稳定运行。
3 参数可调椭圆滑动轴承转子系统试验研究 3.1 试验台的设计与搭建下面是具体试验工作,图 10是自主搭建的转子轴承试验台。如图所示,自主搭建的转子轴承试验台由转子轴承系统、驱动系统、加载系统、润滑系统、测试系统和其他辅助零部件组成。本试验台的全部组成部分都是由课题组自主设计并加工安装,对每一部分都有足够了解,有绝对的控制权,这样有助于试验的进行,能采集到需要的试验数据。其中位移传感器分别安装在轴承支撑处和转子中间位置,测量轴颈的振动,这样的数据采集方案可以测量轴承位置的运转状况和转子的最大振幅,实时监测整个转子轴承系统的工作状态。

|
Download:
|
| 图 10 自主搭建的转子轴承试验台 Fig. 10 View of the experimental layout | |
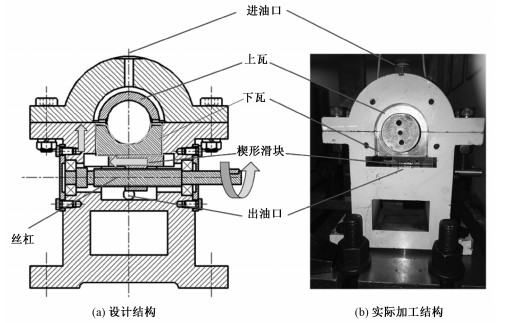
图 11为参数可调椭圆轴承的设计结构和加工后的结构,轴承的上瓦固定,下瓦可以随着丝杠的转动上下滑动。丝杠与下瓦之间通过楔形滑块连接,通过楔形滑块把丝杠的转动转化为下瓦的上下滑动。楔形滑块与下瓦接触的平面的斜度为1:125,丝杆转动一圈,带动滑块移动2 mm,并带动轴瓦上下滑动16 μm。根据前面介绍的椭圆度计算公式可以得到,丝杆每转2圈,对应椭圆度变化0.1。丝杠在原始位置时,轴承为圆轴承,随着丝杠的转动,椭圆度增大,当丝杠转动两圈时,椭圆度为0.1,当丝杠转动14圈时,椭圆度调节到0.7。下面实验的操作过程就是按照这种设计方法,实现椭圆度的调节。
|
Download:
|
| 图 11 参数可调椭圆轴承结构 Fig. 11 View and descriptions of the adjustable elliptical bearing | |
参数可调轴承采用涡轮机油润滑,润滑油从顶端进油口注入,先流经上瓦,上瓦与下瓦的分割面加工油槽,通过油槽可以顺利流到下瓦,当润滑油充满轴承间隙后从侧面溢出,最后流到轴承座下端的油腔,通过抽油泵从出油口带走润滑油。轴承座侧面安装带密封环的端盖(图 11未安装),可调轴承被封装在油腔内,既可以为轴承提供充足的油量,也不会让润滑油溢出。
3.3 试验方案本次实验的目的是研究轴承椭圆度和转速等因素对转子振动的影响。根据实验目的,结合实验台实际情况,设定实验工况,列于表 3中。由于转子在临界转速附近转动时,转子系统会产生很大的振动,对转子的稳定运行造成很大影响,所以试验转速设定在临界转速以外的安全区域,此时转子表现为刚性转子系统。
|
|
表 3 试验工况参数 Table 3 Operating parameters of the test |
试验步骤
1) 将测量好重量的螺柱和螺母旋入加载圆盘的螺孔中,并记下螺柱和螺母的质量和旋入的深度。
2) 打开计算机,连接传感器,确保数据采集系统正常运行。
3) 打开供油泵,开始供油,观察流量计,当供油量达到要求时再进行下一步操作。
4) 调节轴承座丝杠,使轴承的初始椭圆度为0.1。
5) 打开电机开关,调节可控硅直流电机调速控制装置,将转速调节至1 000 rpm,转速的监测用非接触式转速表实现。
6) 采集数据,数据采集时间持续2 min。
7) 再将电机转速调节至2 000 rpm,采集数据。
8) 实验完成后,关闭所有电源,注意在关闭供油泵之前先关闭电机电源。
9) 将轴承椭圆度分别调整为0.2、0.3、0.4、0.5、0.6、0.7,分别重复步骤5)、6)、7)、8)。
采样频率3 000 Hz,每隔10 s测一次,每次测1 s,每个工况测2 min,取典型的轴心轨迹分析。
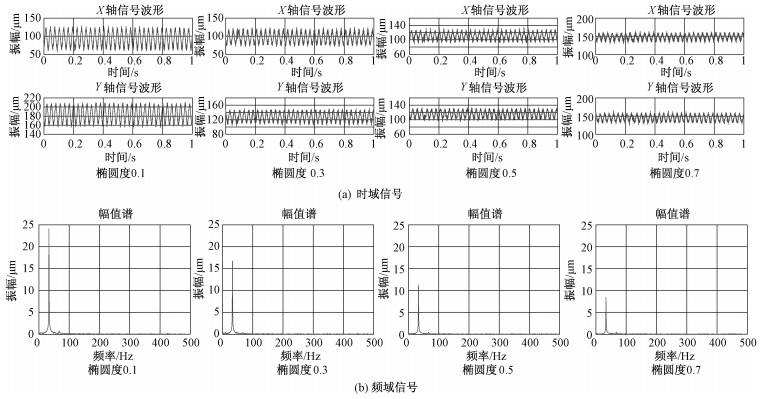
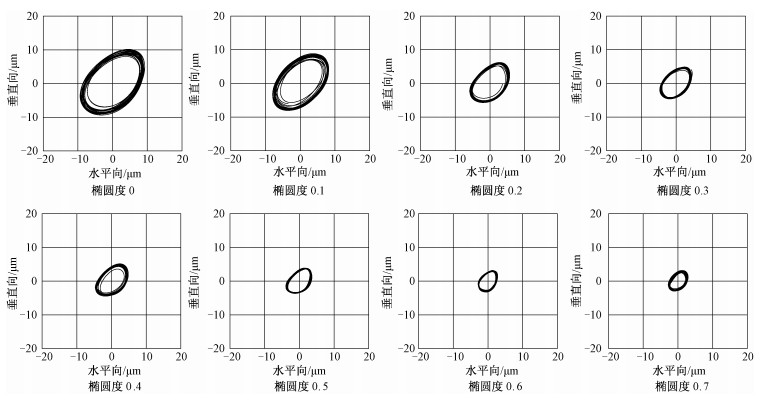
3.4 试验结果分析按照上面介绍的试验步骤,采集不同工况下的试验数据信号,并绘制出对应的时域频域信号图(图 12)。从图中可以观察到时域信号有规律变化,频域信号除转频外,其他信号的赋值很小,采集的信号没有杂质信号干扰,可以绘制出清晰的轴心振动轨迹。图 13是转速为1 000 rpm时,不同椭圆度下采集试验数据,并绘制的轴心轨迹。
|
Download:
|
| 图 12 不同椭圆度下采集数据信号的频谱图(转速为1 000 rpm) Fig. 12 Frequency spectra of acquisitive data signals at different ellipticity values at 1 000 rpm | |
|
Download:
|
| 图 13 不同椭圆度下的轴心轨迹(转速为1 000 rpm) Fig. 13 Axis orbits of journal at different ellipticity values at 1 000 rpm | |
从图 13的试验结果发现转子的轴心轨迹呈椭圆形,在相同的转速工况下,转子振动的振幅随轴承椭圆度的增加而减小;圆轴承支撑时转子的振幅最大,椭圆轴承支撑时振幅小于圆轴承。当椭圆度从0.1,调节到0.7时,轴心轨迹有层次的逐渐减小;当椭圆度调节到最大值时,振幅最小,减小程度可以达到70%以上。
通过实验研究可以观察到,对于刚性转子,通过调节轴承椭圆度,改变油膜间隙,转子的振动明显减小,说明改变椭圆轴承的椭圆度能够有效地抑制振动。并且通过不同椭圆度下试验数据对比得出抑阵作用可以达到70%以上,这与前面的理论研究一致,验证计算结果的正确性。
4 结论1) 轴承椭圆度对刚度阻尼动力学系数产生很大影响。参数可调椭圆轴承具有调节椭圆度特性,通过调节椭圆度改变油膜间隙,可以有效地改变轴承的刚度和阻尼系数。
2) 参数可调轴承能有效抑制转子的振动,调节椭圆度可以使临界转速的振幅减小70%,并且水平和垂直方向振幅的减小程度几乎相同。通过调节轴承椭圆度,改变油膜间隙,转子的振动明显减小,说明改变椭圆轴承的椭圆度能够有效地抑制振动。
3) 由于试验转速设定在临界转速以外的区域,转子表现为刚性转子系统。当椭圆度从0.1调节到0.7时,轴心轨迹有层次的逐渐减小,椭圆度调节到最大值时,振幅最小,减小程度可以达到70%以上。这与前面的理论计算结果一致,验证理论计算的正确性。
| [1] |
Lee A S, Kim B O, Kim Y C. A finite element transient response analysis method of a rotor-bearing system to base shock excitations using the state-space Newmark scheme and comparisons with experiments[J]. Journal of Sound & Vibration, 2006, 297(3): 595-615. |
| [2] |
Han Q K, Chu F L. Parametric instability of flexible rotor-bearing system under time-periodic base angular motions[J]. Applied Mathematical Modelling, 2015, 39(15): 4511-4522. DOI:10.1016/j.apm.2014.10.064 |
| [3] |
刘树鹏.舰船纵横倾作用下转子轴承系统动力学特性研究[D].哈尔滨: 哈尔滨工业大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10213-1012000798.htm
|
| [4] |
Dhawan R, Verma S. Analyzing micropolar lubrication in noncircular hybrid journal bearings[J]. Tribology Transactions, 2014, 57(2): 182-189. DOI:10.1080/10402004.2013.859337 |
| [5] |
Schweizer B. Total instability of turbocharger rotors:physical explanation of the dynamic failure of rotors with full-floating ring bearings[J]. Journal of Sound and Vibration, 2009, 328(1): 156-190. |
| [6] |
Schweizer B. Dynamics and stability of turbocharger rotors[J]. Archive of Applied Mechanics, 2010, 80(9): 1017-1043. DOI:10.1007/s00419-009-0331-0 |
| [7] |
Schweizer B. Oil whirl, oil whip and whirl/whip synchronization occurring in rotor systems with full-floating ring bearings[J]. Nonlinear Dynamics, 2009, 57(4): 509-532. DOI:10.1007/s11071-009-9466-3 |
| [8] |
Prabhakaran N, Sukumaran N, Jayadas N. Static and dynamic analysis of elastohydrodynamic elliptical journal bearing with micropolar lubricant[J]. TribologyInternational, 2007, 40(1): 297-305. |
| [9] |
Rahmatabadi A D, Nekoeimehr M, Rashidi R. Micropolar lubricant effects on the performance of noncircular lobed bearings[J]. Tribology International, 2010(43): 404-413. |
| [10] |
陈红霞, 陈国定, 李盼. 偏载条件下椭圆轴承的静动特性[J]. 润滑与密封, 2013, 38(1): 66-73. |
| [11] |
张宏献, 徐武彬, 王镇江, 等. 椭圆度对椭圆滑动轴承稳定性的影响[J]. 中国机械工程, 2011, 22(20): 2466-2468. |
| [12] |
张磊, 裴世源, 徐华. 摇摆工况下两种舰船转子轴承系统的安全性与稳定性研究[J]. 中国科学:技术科学, 2018, 48(4): 369-381. |
| [13] |
张磊, 裴世源, 徐华, 等. 摇摆工况下椭圆轴承转子系统动力学特性研究[J]. 机械设计与制造, 2018(7): 100-103. DOI:10.3969/j.issn.1001-3997.2018.07.029 |
| [14] |
张磊, 裴世源, 徐华, 等. 摇摆工况下错位瓦轴承支撑的转子系统动力学特性[J]. 中国机械工程, 2017, 28(18): 2161-2170. DOI:10.3969/j.issn.1004-132X.2017.18.003 |
 2019, Vol. 36
2019, Vol. 36 


