Let R be a ring with unit. The Bass Nil groups N^mK_i(R) are introduced by Bass^[1] in order to investigate the relation between K_i(R[x₁, …, x_m]) and K_i(R). For any i∈$\mathbb{Z}$, NK_i(R) is defined to be the kernel of surjective map K_i(R[x₁])→K_i(R) induced by x₁ |→0. And N^mK_i(R) is defined by iteration, i.e., the kernel of the surjection N^m-1K_i(R[x_m])→N^m-1K_i(R) induced by x_m |→0. When i=0, 1, 2, K_i(R) are the classical algebraic K-groups defined by Grothendieck^[2], Bass^[1] and Milnor^[3], respectively. When i < 0, the negative K-theory is defined by Bass^[1]. When i>2, K_i(R)=π_i(K(R)) is defined to be the i-th homotopy group of the K-theory space K(R) which was first invented by Quillen^[4] via plus-construction or Q-construction. As for the Bass Nil groups, the most known property is the following phenomenon.

Theorem A (See Refs. [5-9]). Let R be a ring. For any i, m∈$\mathbb{Z}$ and m≥1, if N^mK_i(R)≠0, then it is not finitely generated as an abelian group.

Let p be a prime number. In some cases, NK_i(R) are abelian p-groups^[8]. However, the exponents of these abelian p-groups are not completely determined. For example, the exponents of NK₀($\mathbb{Z}$[C₄]) and NK₁($\mathbb{Z}$[C₄]) are both 2, but the exponent of NK₂($\mathbb{Z}$[C₄]) is still unknown^[10].

Let $\mathbb{F}$ be a finite field of characteristic p and C_pⁿ the cyclic p-group of order pⁿ. Since K₂($\mathbb{F}$[C_pⁿ])=K₂($\mathbb{F}$)=0 (see Ref. [11]), we have

$ \begin{array}{*{20}{c}} {{K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]\left[ {{x_1}, \cdots ,{x_m}} \right]} \right) \cong {{\left( {1 + N} \right)}^m}{K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]} \right) = } \\ {\mathop \oplus \limits_{i = 1}^m \left( {\begin{array}{*{20}{c}} m \\ i \end{array}} \right){N^i}{K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]} \right).} \end{array} $

In Ref. [12], Juan-Pineda showed the non-finiteness of NK₂($\mathbb{F}$_p[C_pⁿ]) by giving one non-trivial element of order p and concluded that NK₂($\mathbb{Z}$[C])≠0 for any non-trivial cyclic group C. In this paper, we could give infinitely many non-trivial elements of order p^l for any 1≤l≤n in N^mK₂($\mathbb{F}$[C_pⁿ]). In fact, we give a presentation of N^mK₂($\mathbb{F}$[C_pⁿ]) in terms of Dennis-Stein symbols and show that the exponent of N^mK₂($\mathbb{F}$[C_pⁿ]) is pⁿ.

1 Main result

Let $\mathbb{F}$ be a finite field with p^f elements and B={1, b, b², …, b^f-1} a basis of $\mathbb{F}$ as a vector space over the finite field $\mathbb{F}$_p of p elements. Let C_pⁿ be the cyclic group of order pⁿ (n≥1) generated by σ. Let J=J($\mathbb{F}$[C_pⁿ]) be the Jacobson radical of the group algebra $\mathbb{F}$[C_pⁿ]. The notation $\oplus $_∞ denotes a countably infinite direct sum, i.e., $\oplus $_∞=$\oplus $_s∈S for some countably infinite set S.

Lemma 1.1 NK₂($\mathbb{F}$[C_pⁿ])$\cong $K₂($\mathbb{F}$[C_pⁿ][x], J[x]).

Proof Observe that $\mathbb{F}$[C_pⁿ][x]/J[x]$\cong $$\mathbb{F}$[x] and $\mathbb{F}$[x]→$\mathbb{F}$[C_pⁿ][x] is a split inclusion. Since $\mathbb{F}$ is a finite field, K₂($\mathbb{F}$[C_pⁿ])=K₂($\mathbb{F}$)=0. And K₂($\mathbb{F}$[x])=K₂($\mathbb{F}$)$\oplus $NK₂($\mathbb{F}$)=0 because $\mathbb{F}$ is regular. Hence the result follows from the two exact sequences of K-groups:

$ \begin{array}{*{20}{c}} {0 \to {K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]\left[ x \right],J\left[ x \right]} \right) \to {K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]\left[ x \right]} \right)} \\ { \to {K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]\left[ x \right]/J\left[ x \right]} \right) = 0 \to 0,} \end{array} $

$ \begin{array}{*{20}{c}} {0 \to N{K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]} \right) \to {K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]\left[ x \right]} \right) \to } \\ {{K_2}\left( {\mathbb{F}\left[ {{C_{{p^n}}}} \right]} \right) = 0 \to 0.} \end{array} $

Let I=(t₁^pn) be a proper ideal in the polynomial ring $\mathbb{F}$[t₁, t₂, …, t_m+1]. Then

$ \mathbb{F}\left[ {{C_{{p^n}}}} \right] \cong \mathbb{F}\left[ {{t_1}} \right]/\left( {t_1^{{p^n}}} \right), $

$ \mathbb{F}\left[ {{C_{{p^n}}}} \right]\left[ {{x_1}, \cdots ,{x_m}} \right] \cong \mathbb{F}\left[ {{t_1}, \cdots ,{t_{m + 1}}} \right]/I, $

via σ-1 |→t₁ and x_i |→t_i+1. Let A=$\mathbb{F}$[t₁, …, t_m+1]/I and M=($\overline {{t_1}} $) be its nilradical where $\overline {{t_1}} $=t₁+I. Then $\mathbb{F}$[x₁, …, x_m]$\cong $A/M and K₂(A)$\cong $K₂(A, M). So the above lemma becomes NK₂($\mathbb{F}$[C_pⁿ])$\cong $K₂($\mathbb{F}$[t₁, t₂]/I, M) (m=1).

Lemma 1.2 Let 1≤t≤n-1 and 1≤h < p be integers. If p^n-t-1 < k≤p^n-t, $\left\lceil {{\rm{lo}}{{\rm{g}}_p}\frac{{{p^n} + 1}}{{pk}}} \right\rceil = \left\lceil {{\rm{lo}}{{\rm{g}}_p}\frac{{{p_n}}}{{pk-h}}} \right\rceil = t$, and if k=1, $\left\lceil {{\rm{lo}}{{\rm{g}}_p}\frac{{{p^n} + 1}}{{pk}}} \right\rceil = \left\lceil {{\rm{lo}}{{\rm{g}}_p}\frac{{{p_n}}}{{pk-h}}} \right\rceil = n$, where $\left\lceil a \right\rceil $=min{s∈$\mathbb{Z}$|s≥a} denotes the smallest integer no less than a.

Proof If k=1, the computation is easy. Suppose p^n-t-1+1≤k≤p^n-t, the result follows from the inequalities

$ {p^{t - 1}} < \frac{{{p^n}}}{{{p^{n - t + 1}} - h}} \le \frac{{{p^n}}}{{pk - h}} \le \frac{{{p^n}}}{{{p^{n - t}} + p - h}} < {p^t}, $

$ {p^{t - 1}} = \frac{{{p^n}}}{{{p^{n - t + 1}}}} < \frac{{{p^n} + 1}}{{pk}} \le \frac{{{p^n} + 1}}{{{p^{n - t}} + p}} < {p^t}. $

Theorem 1.1 Let C_pⁿ be the cyclic group of order pⁿ (n≥1) generated by σ. For any integer m≥1, N^mK₂($\mathbb{F}$[C_pⁿ])$\cong $$\oplus $_∞($\mathop \oplus \limits_{i = 1}^n $$\mathbb{Z}$/pⁱ$\mathbb{Z}$) can be generated by these elements:

the generators of order p^l (1≤l≤n-1) are 〈b(σ-1)^pk-1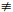$\prod\limits_{j = 1}^m {} $x_j^β_j, (σ-1)〉, where p^n-l-1 < k≤p^n-l and gcd(p, β₁, …, β_m)=1, 〈b(σ-1)^pk($\prod\limits_{j = 1}^m {} $x_j^β_j)/x_i, x_i〉, where 1≤i≤m, p^n-l-1≤k < p^n-l, gcd(p, β₁, …, β_m)=1 and i≠min{j|β_j0 mod p}, 〈b(σ-1)^pk-h($\prod\limits_{j = 1}^m {} $x_j^β_j)/x_i, x_i〉, where 1≤i≤m, p^n-l-1 < k≤p^n-l, 1≤h < p; and generators of order pⁿ are 〈b(σ-1)^p-1$\prod\limits_{j = 1}^m {} $x_j^β_j, (σ-1)〉, where gcd(p, β₁, …, β_m)=1, 〈b(σ-1)^h($\prod\limits_{j = 1}^m {} $x_j^β_j)/x_i, x_i〉, where 1≤i≤m and 1≤h < p.

For all the above symbols, b∈B and β=(β₁, …, β_m)∈$\mathbb{N}$₊^m, where $\mathbb{N}$₊ is the set of positive integers.

Proof Suppose we get a generating set of K₂($\mathbb{F}$[C_pⁿ][x₁, …, x_m])$\cong $K₂(A, M) in terms of Dennis-Stein symbols. Fix j different indeterminates in {x₁, …, x_m}, say {x_i1, …, x_ij}. The elements of the direct summand N^jK₂($\mathbb{F}$[C_pⁿ])K₂($\mathbb{F}$[C_pⁿ][x_i1, …, x_ij])K₂($\mathbb{F}$[C_pⁿ][x₁, …, x_m]) can be represented by using those Dennis-Stein symbols containing these j different indeterminates. Hence K₂($\mathbb{F}$[C_pⁿ][x₁, …, x_m]) contains mj pieces of N^jK₂($\mathbb{F}$[C_pⁿ]). So the elements of N^mK₂($\mathbb{F}$[C_pⁿ]) can be represented by using those Dennis-Stein symbols in K₂($\mathbb{F}$[C_pⁿ][x₁, …, x_m]) containing all the m indeterminates.

We follow the notations in Ref. [13]. Let $\mathbb{N}$={0, 1, 2…} be the set of non-negative integers and $\mathbb{N}$+={1, 2, 3, …} the set of positive integers. Let εi=(0, …, 0, 1, 0, …, 0)∈$\mathbb{N}$m+1 be the i-th basis vector. For α∈$\mathbb{N}$m+1, write tα=t1α1…tαm+1m+1 where t1=σ-1 and ti+1=xi for 1≤i≤m. Define

$ \Delta ' = \left\{ {\alpha = \left( {{\alpha _1}, \cdots ,{\alpha _{m + 1}}} \right) \in \mathbb{N}_ + ^{m + 1}\left| {{\alpha _1} \geqslant {p^n}} \right.} \right\}, $

$ \Lambda ' = \left\{ {\left( {\alpha ,i} \right) \in \mathbb{N}_ + ^{m + 1} \times \left\{ {1,2, \cdots ,m + 1} \right\}} \right\}. $

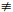
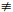
For (α, i)∈Λ′, let [α, i]=min{k∈$\mathbb{Z}$|kα-εⁱ∈Δ′} and w(α, i)=min{w∈$\mathbb{N}$|p^w≥[α, i]}. Then [α, 1]=$\left\lceil {\frac{{{p^n} + 1}}{{{\alpha _1}}}} \right\rceil $, [α, j]=$\left\lceil {\frac{{{p^n}}}{{{\alpha _1}}}} \right\rceil $ for any j≠1. If gcd(p, α₁, …, α_m+1)=1, put [α]=max{[α, i]|α_i0 mod p}. Set Λ′⁰={(α, i)∈Λ′| gcd(p, α₁, …, α_m+1)=1, i≠min{j|α_j0 mod p, [α, j]=[α]}}, and let Λ′_>1⁰={(α, i)∈Λ′⁰|[α, i]>1}.

Then by Corollary 2.7 in Ref. [13] and the above discussion, N^mK₂($\mathbb{F}$[C_pⁿ]) has a presentation with

generators: 〈bt^α-εi, t_i〉, where b∈B, (α, i)∈Λ′_>1⁰;

relations: p^{w(α, i)}〈bt^α-εi, t_i〉=0, where w(α, i)=「log_p[α, i].

It is sufficient to determine the set Λ′_>1⁰.

If α₁=pⁿ and at least one of α_j with p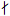α_j, then only (α, 1)∈Λ′_>1⁰ and [α, 1]=2.

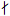
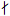
If α₁=pk for some 1≤k < p^n-1 and j is the smallest number such that pα_j, i.e., p|α₁, …, p|α_j-1 and pα_j, then all (α, i) except (α, j) are in Λ′_>1⁰.

If p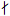α₁, i.e., α₁=pk-h for some 1≤k≤p^n-1 and 1≤h < p, then for each j≥2, (α, j)∈Λ′_>1⁰.

So one gets

$ \begin{array}{*{20}{c}} {\Lambda {'}_{ > 1}^0 = \left\{ {\left( {\alpha ,1} \right)\left| {{\alpha _1} = {p^n},\gcd } \right.\left( {p,{\alpha _2}, \cdots ,{\alpha _{m + 1}}} \right) = 1} \right\}}\\ { \cup \left\{ {\left( {\alpha ,i} \right)\left| {\begin{array}{*{20}{c}} {{\alpha _1} = pk,1 \le k < {p^{n - 1}},}\\ {\gcd \left( {p,{\alpha _2}, \cdots ,{\alpha _{m + 1}}} \right) = 1,}\\ {i \ne \min \left\{ {j\left| {{\alpha _j} ≢ 0\bmod p} \right.} \right\}} \end{array}} \right.} \right\}}\\ { \cup \left( {\mathop \cup \limits_{j = 2}^{m + 1} \left\{ {\left( {\alpha ,j} \right)\left| {\begin{array}{*{20}{c}} {{\alpha _1} = pk - h,}\\ {1 \le k \le {p^{n - 1}},}\\ {1 \le h < \rho } \end{array}} \right.} \right\}} \right).} \end{array} $

Let b∈B. For any β∈$\mathbb{N}$₊^m, write x^β=x₁^β₁x₂^β₂…x_m^β_m. We can get a presentation of N^mK₂($\mathbb{F}$[C_pⁿ]) in terms of the following Dennis-Stein symbols with generators

·〈b(σ-1)^pk-1x^β, (σ-1)〉 where 1≤k≤p^n-1 and gcd (p, β₁, …, β_m)=1;

·〈b(σ-1)^pkx^β-εi, x_i〉 where 1≤k < p^n-1, gcd (p, β₁, …, β_m)=1 and i≠min{j|β_j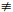0 mod p};

·〈b(σ-1)^pk-hx^β-εi, x_i〉 where 1≤k≤p^n-1, 1≤h < p, 1≤i≤m.

The relations are

$ \cdot \;\;{p^{\left\lceil {{{\log }_p}\frac{{{p^n} + 1}}{{pk}}} \right\rceil }}\left\langle {b{{\left( {\sigma - 1} \right)}^{pk - 1}}{x^\beta },\left( {\sigma - 1} \right)} \right\rangle = 0, $

$ \cdot \;\;{p^{\left\lceil {{{\log }_p}\frac{{{p^n}}}{{pk}}} \right\rceil }}\left\langle {b{{\left( {\sigma - 1} \right)}^{pk}}{x^{\beta - {\varepsilon ^i}}},{x_i}} \right\rangle = 0, $

$ \cdot \;\;{p^{\left\lceil {{{\log }_p}\frac{{{p^n}}}{{pk - h}}} \right\rceil }}\left\langle {b{{\left( {\sigma - 1} \right)}^{pk - h}}{x^{\beta - {\varepsilon ^i}}},{x_i}} \right\rangle = 0. $

Then by Lemma 1.2, the result follows.

2 Examples

Example 2.1 Let C₄ be the cyclic group of order 4 generated by σ. Then NK₂($\mathbb{F}$₂[C₄])$\cong $$\oplus $_∞($\mathbb{Z}$/2$\mathbb{Z}$$\oplus $$\mathbb{Z}$/4$\mathbb{Z}$) can be generated by these elements: the generators of order 4 are

$ \left\{ {\left\langle {\left( {\sigma - 1} \right){x^{i - 1}},x} \right\rangle \left| {i \ge 1} \right.} \right\}, $

$ \left\{ {\left\langle {\left( {\sigma - 1} \right){x^{2i - 1}},\left( {\sigma - 1} \right)} \right\rangle \left| {i \ge 1} \right.} \right\}, $

and the generators of order 2 are

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^3}{x^{i - 1}},x} \right\rangle \left| {i \ge 1} \right.} \right\}, $

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^3}{x^{2i - 1}},\left( {\sigma - 1} \right)} \right\rangle \left| {i \ge 1} \right.} \right\}. $

$ {N^2}{K_2}\left( {{\mathbb{F}_2}\left[ {{C_4}} \right]} \right) \cong { \oplus _\infty }\left( {\mathbb{Z}/2\mathbb{Z}\; \oplus \;\mathbb{Z}/4\mathbb{Z}} \right) $

N²K₂($\mathbb{F}$₂[C₄])$\cong $$\oplus $_∞($\mathbb{Z}$/2$\mathbb{Z}$$\oplus $$\mathbb{Z}$/4$\mathbb{Z}$) can be generated by these elements: the generators of order 4 are

$ \left\{ {\left\langle {\left( {\sigma - 1} \right){x^{i - 1}}{y^j},x} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {\left( {\sigma - 1} \right){x^i}{y^{j - 1}},y} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {\left( {\sigma - 1} \right){x^{2i - 1}}{y^j},\left( {\sigma - 1} \right)} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {\left( {\sigma - 1} \right){x^{2i}}{y^{2j - 1}},\left( {\sigma - 1} \right)} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

and the generators of order 2 are

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^3}{x^{i - 1}}{y^j},x} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^3}{x^i}{y^{j - 1}},y} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^2}{x^{2i - 1}}{y^{2j - 1}},x} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^2}{x^{2i - 1}}{y^{j - 1}},y} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^3}{x^{2i - 1}}{y^j},\left( {\sigma - 1} \right)} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

$ \left\{ {\left\langle {{{\left( {\sigma - 1} \right)}^3}{x^{2i}}{y^{2j - 1}},\left( {\sigma - 1} \right)} \right\rangle \left| {i \ge 1} \right.,j \ge 1} \right\}, $

where x, y are indeterminates.

Corollary 2.1 NK₁($\mathbb{Z}$[C_p²])$\cong $$\oplus $_∞$\mathbb{Z}$/p$\mathbb{Z}$.

Proof Assume C_p² is generated by σ. There is a Milnor square,

where ζ_p² is a primitive p²-th root of unity and $\mathbb{Z}$[ζ_p²] is the ring of integers in Q(ζ_p²). By the Mayer-Vietoris sequence for NK-functors, we get an exact sequence

$ \begin{array}{*{20}{c}} {N{K_2}\left( {\mathbb{Z}\left[ {{C_{{p^2}}}} \right]} \right) \to N{K_2}\left( {\mathbb{Z}\left[ {{\zeta _{{p^2}}}} \right]} \right) \oplus } \\ {N{K_2}\left( {\mathbb{Z}\left[ {{C_p}} \right]} \right) \to N{K_2}\left( {{\mathbb{F}_p}\left[ {{C_p}} \right]} \right) \to } \\ {N{K_1}\left( {\mathbb{Z}\left[ {{C_{{p^2}}}} \right]} \right) \to N{K_1}\left( {\mathbb{Z}\left[ {{\zeta _{{p^2}}}} \right]} \right) \oplus N{K_1}\left( {\mathbb{Z}\left[ {{C_p}} \right]} \right).} \end{array} $

Since $\mathbb{Z}$[ζ_p²] is regular, NK_n($\mathbb{Z}$[ζ_p²])=0 for all n. The order of C_p is square-free. Hence NK₁($\mathbb{Z}$[C_p])=0 (see Ref. [14]). And NK₂($\mathbb{Z}$[C_p])$\cong $$\oplus $_∞$\mathbb{Z}$/p$\mathbb{Z}$ (see Ref. [15]). So the above exact sequence becomes

$ \begin{array}{*{20}{c}} {N{K_2}\left( {\mathbb{Z}\left[ {{C_p}} \right]} \right) \to N{K_2}\left( {{\mathbb{F}_p}\left[ {{C_p}} \right]} \right) \to } \\ {N{K_1}\left( {\mathbb{Z}\left[ {{C_{{p^2}}}} \right]} \right) \to 0.} \end{array} $

Moreover, we have NK₂($\mathbb{F}$_p[C_p])$\cong $$\oplus $_∞$\mathbb{Z}$/p$\mathbb{Z}$ and NK₁($\mathbb{Z}$[C_p²])≠0 (see Ref. [14]). Hence NK₁($\mathbb{Z}$[C_p²]) is not finitely generated, therefore NK₁($\mathbb{Z}$[C_p²])$\cong $$\oplus $_∞$\mathbb{Z}$/p$\mathbb{Z}$.