2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar,SAR)利用载机在方位向的移动形成一个等效长天线。通过对接收回波进行一定的处理改善垂直波束方向的分辨率,从而获取地表二维图像。成像处理算法分为频域算法和时域算法,频域算法成像效率较高(O(N2logN)),应用较为广泛,如RD(range doppler),CS(chirp scaling)和ωK等算法。然而,对于机载SAR系统,频域算法对不同算法、不同模式、不同斜视角、不同地形和不同波段等情况需要研究对应的不同的运动补偿方法[1-2](motion compensation,MOCO),而且有许多繁琐复杂的细节需要考虑,在现今SAR模式日益增多,需求日益多样的情况下难以满足通用化的需求; 而时域算法的运动补偿则更为通用化。另一方面,频域补偿算法由于存在波束中心假设和平地假设,其精度也比不上时域算法。时域算法最大的缺点是效率低,针对这一问题,一方面随着处理器运算能力的提高逐渐得以克服,另一方面各类快速算法相继被提出。
BP[3](back projection)算法是时域算法的典型代表,主要思想是对每一个像素点都利用一个独特的匹配滤波器进行处理。逐点成像使得BP算法具有精度高、效率低以及易于并行化的特点。针对效率低的问题,一方面可以充分利用近年并行处理器运算能力提高的优势,另一方面是研究快速BP算法。目前快速BP主要分为两类,一类是利用局部近似的快速分解因子BP算法(fast factorized back projection,FFBP)[4-6],文献[4]提出局部BP(local back projection,LBP)算法,利用在地理位置上相近的两个点在相近的孔径上有近似相等的距离实现加速,当把
本文提出一种把FFBP和CMBP算法二者融合的快速BP算法,即基于方位调制的快速因子分解BP算法(chirp modulated fast factorized back projection,CMFFBP)。首先通过ωK算法对原始数据进行预处理,再人为引入一个线性调频信号在二维频域对方位向进行调制,在等效距离下利用FFBP算法的思想进行后向投影。值得注意的是,FFBP算法利用的是真实距离,而所提算法利用的是等效距离。分析表明,在等效距离下,FFBP算法中极角的物理意义保持不变,空间上相邻的点仍然有近似相等的等效距离。所以,能够在等效距离下把原始数据投影到中心距离线上,从而结合两种方法的优势,提高快速BP算法的效率。分析表明,所提算法能够并行实现,通过多核CPU(central processing unit)或GPU(graphics processing unit)进一步提高效率。在机载实时成像和卫星在轨实时成像方面有一定的应用潜力,因为载机或卫星上的实时处理需要在硬件资源有限的条件下尽可能地提高速度,对算法效率要求较高。仿真和实测数据实验均表明,所提方法和已有的两类快速BP算法相比,在几乎不损失精度的情况下明显提高了效率。
1 SAR回波模型本文限定回波模型建立在机载SAR基础上,所提算法也适用于星载SAR的成像;假设SAR是条带模式且为右正侧视;假设成像场景中只有一个点目标,由叠加定理,以下分析对多个目标也是适用的;为便于分析,假设距离向和方位向所加的窗均为矩形窗。
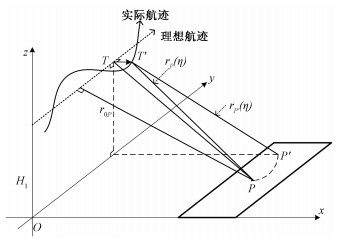
如图 1,P是地面上的一个点目标,假设其散射系数为1,SAR系统的实际航迹近似水平且匀速直线,实际航迹由于大气影响相对于理想航迹存在一定的偏离。
|
Download:
|
| 图 1 SAR回波模型及运动补偿示意图 Fig. 1 SAR echo model and motion compensation | |
在某时刻,SAR天线位置处于实际航迹上的点T′,其相对于理想航迹上的点T在x和z轴方向有偏移(δxT, δzT)。SAR系统在T′位置接收线性调频信号并经解调和距离压缩后,其信号形式为
| $ \begin{array}{*{20}{c}} {s\left( {t,\eta } \right) = \sin {\rm{c}}\left( {{B_r}\left( {t - {\tau _P}\left( \eta \right)} \right)} \right) \cdot }\\ {{\rm{rect}}\left( {\frac{\eta }{{{T_{aP}}}}} \right)\exp \left( { - {\rm{j}}2\pi {f_c}{\tau _P}\left( \eta \right)} \right).} \end{array} $ | (1) |
式中:t为快时间;η为慢时间,定义η=0时,SAR最接近点目标P;Br为距离向带宽;TaP为点目标P对应的合成孔径时间(严格来说,由于SAR偏离理想航迹,TaP和方位向时间η的偏离量(δxη, δzη)有关,但偏离量很小,可忽略);c为光速; τP(η)=2rP(η)/c为双程时间延迟;rP(η)可以表示为
| $ {r_P}\left( \eta \right) = \sqrt {r_{0P}^2 + {v^2}{\eta ^2}} + {r_{eP}}\left( \eta \right). $ | (2) |
式中:r0P是目标点P到理想航迹的最近距离;v是方位向的速度,通常假设其为常数(实际中一般通过方位向重采样以补偿方位向速度不恒定带来的误差)。因为
机载SAR由于易受大气影响,实际飞行时会偏离理想航迹,需要进行MOCO。本文所提算法采用DMA[9](direct MOCO algorithm)对距离压缩后的信号进行运动补偿,该方法采用平地假设和波束中心近似,其优点是不像传统两阶运动补偿法中在距离徙动校正之后进行距离向空变误差补偿,而能够在距离徙动校正之前进行。
根据文献[9],残余运动误差为
| $ {r_{{\rm{res,}}P}}\left( \eta \right) = {r_{eP}}\left( \eta \right) - {r_{{\mathop{\rm ref}\nolimits} }}\left( \eta \right). $ | (3) |
式中:rref(η)为参考斜距处的空不变运动误差,与航迹偏离量有关。
残余运动误差分为距离空变误差和方位空变误差,分别为
| $ {r_{re,P}}\left( \eta \right) = {r_{ep'}}\left( \eta \right) - {r_{{\mathop{\rm ref}\nolimits} }}\left( \eta \right), $ | (4) |
| $ {r_{ae,P}}\left( \eta \right) = {r_{eP}}\left( \eta \right) - {r_{eP'}}\left( \eta \right). $ | (5) |
式中:P′如图 1所示,满足rP(η)=rP′(η),且其方位向和T′一样。在频域算法中,空不变和距离向空变的运动误差之和为reP′(η),由于reP′(η)不依赖于方位位置T(因为P′的方位位置和η是一样的,可以通过P′确定其方位),只依赖于在该方位位置的偏离量,所以可通过距离向插值重采样和相位相乘得以补偿。运动补偿后的信号为
| $ \begin{array}{*{20}{c}} {{s_1}\left( {t,\eta } \right) = \sin {\rm{c}}\left( {{B_r}\left( {t - {{\tau '}_P}\left( \eta \right)} \right)} \right) \cdot }\\ {{\rm{rect}}\left( {\frac{\eta }{{{T_{aP}}}}} \right)\exp \left( { - {\rm{j}}2\pi {f_c}{{\tau '}_P}\left( \eta \right)} \right).} \end{array} $ | (6) |
其中,τ′P(η)=2r′P(η)/c,
| $ {{r'}_P}\left( \eta \right) = \sqrt {r_P^2 + {v^2}{\eta ^2}} + {r_{ae,P}}\left( \eta \right). $ | (7) |
式中:rae, P(η)为方位空变误差,是由于平地假设和波束中心近似带来的,其误差依赖于地形和孔径。频域算法对方位空变误差的补偿通常较繁琐而且难以避免一些近似,如各种子孔径或自聚焦算法[10-12],而BP算法可以很好地解决这个问题,其逐点成像的过程保证可以将图像空间中的方位向和航迹中的方位向分开,从而可以通过在后向投影过程中用真实距离rP(η),不经修改即可完成方位空变误差的运动补偿。通过引入外部数字高程模型(digital elevation model,DEM),可以补偿地形起伏带来的误差。
受时域算法运动补偿思想的影响,文献[5]提出利用BP算法实现对方位空变的补偿,同时为避免BP算法效率低的问题,人为引入线性调频项减少等效合成孔径长度,很好地兼顾了效率和精度。
2.2 ωK和方位调制处理标准ωK算法已经很成熟了,故在此只给出主要推导结果。对式(6)运用驻定相位原理(principle of stationary phase,POSP),其二维频域为
| $ \begin{array}{l} {S_1}\left( {{f_t},{f_\eta }} \right) \approx {\rm{rect}}\left( {\frac{{{f_t}}}{{{B_r}}}} \right){\rm{rect}}\left( {\frac{{{f_\eta }}}{{{B_{aP}}}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - {\rm{j}}\frac{{4\pi \left( {{f_c} + {f_t}} \right)}}{c}{r_{ae,P}}\left( \eta \right)} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - {\rm{j}}\frac{{4\pi {r_P}}}{c}\sqrt {{{\left( {{f_c} + {f_t}} \right)}^2} - \frac{{{c^2}f_\eta ^2}}{{4{v^2}}}} } \right). \end{array} $ | (8) |
式中:ft和fη分别为距离向和方位向频率; BaP为P点位置的方位向带宽。上述存在两个近似,第一个是在运用POSP算方位向时频关系时忽略了reP(η),第二个是方位向带宽BaP其实和ft,fη都有关系,上述两个近似影响很小可忽略。
参考函数相乘,得
| $ \begin{array}{l} {S_2}\left( {{f_t},{f_\eta }} \right) = {\rm{rect}}\left( {\frac{{{f_t}}}{{{B_r}}}} \right){\rm{rect}}\left( {\frac{{{f_\eta }}}{{{B_{aP}}}}} \right) \cdot \\ \;\;\;\;\exp \left( { - {\rm{j}}\frac{{4\pi \left( {{r_P} - {R_{{\mathop{\rm ref}\nolimits} }}} \right)}}{c}\sqrt {{{\left( {{f_c} + {f_t}} \right)}^2} - \frac{{{c^2}f_\eta ^2}}{{4{v^2}}}} } \right) \cdot \\ \;\;\;\;\exp \left( { - {\rm{j}}\frac{{4\pi \left( {{f_c} + {f_t}} \right)}}{c}{r_{ae,P}}\left( \eta \right)} \right). \end{array} $ | (9) |
式中:Rref为参考斜距。
Stolt插值后,信号为
| $ \begin{array}{l} {S_3}\left( {{{f'}_t},{f_\eta }} \right) = {\rm{rect}}\left( {\frac{{{f_t}}}{{{B_r}}}} \right){\rm{rect}}\left( {\frac{{{f_\eta }}}{{{B_{aP}}}}} \right) \cdot \\ \;\;\;\;\exp \left( { - {\rm{j}}\frac{{4\pi \left( {{r_P} - {R_{{\mathop{\rm ref}\nolimits} }}} \right)\left( {{f_c} + {{f'}_t}} \right)}}{c}} \right) \cdot \\ \;\;\;\;\exp \left( { - {\rm{j}}\frac{{4\pi \left( {{f_c} + {f_t}} \right)}}{c}{r_{ae,P}}\left( \eta \right)} \right). \end{array} $ | (10) |
其中,
| $ {{f'}_t} = \sqrt {{{\left( {{f_c} + {f_t}} \right)}^2} - \frac{{{c^2}f_\eta ^2}}{{4{v^2}}}} - {f_c}. $ | (11) |
式(11)即为Stolt变换。
经过CMBP算法的方位调制后,信号为
| $ {S_4}\left( {{{f'}_t},{f_\eta }} \right) = {S_3}\left( {{{f'}_t},{f_\eta }} \right)\exp \left( {{\rm{j}}\frac{{\pi ac{R_{{\mathop{\rm ref}\nolimits} }}}}{{2{v^2}\left( {{f_c} + {{f'}_t}} \right)}}f_\eta ^2} \right). $ | (12) |
式中:a(0<a<1)为调制因子。对式(12)进行二维逆傅里叶变换,为了和式(1)中的方位向时间相区别,设此时的方位向时间为η′,在文献[7]基础上忽略残差的一阶导以及Stolt变换对距离包络的影响,得
| $ \begin{array}{l} {s_4}\left( {t,\eta '} \right) = \sin {\rm{c}}\left( {{B_r}\left( {t - {{\tau ''}_P}\left( {\eta '} \right)} \right)} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{rect}}\left( {\frac{{\eta '}}{{{{T'}_a}}}} \right)\exp \left( { - {\rm{j}}2\pi {f_c}{{\tau ''}_P}\left( {\eta '} \right)} \right). \end{array} $ | (13) |
式中:T′a=aRrefθbw,θbw为方位向波束宽度;
| $ \begin{array}{*{20}{c}} {{{\tau ''}_P}\left( {\eta '} \right) = {r_{0P}} - {R_{{\mathop{\rm ref}\nolimits} }} + \frac{{{v^2}{{\eta '}^2}}}{{2a{R_{{\mathop{\rm ref}\nolimits} }}}} + }\\ {\frac{{{r_{0P}}}}{{\sqrt {r_{0P}^2 + {v^2}{{\eta '}^2}} }}{{r'}_{ae,P}}\left( {\eta '} \right).} \end{array} $ | (14) |
其中,
| $ {{r'}_{ae,P}}\left( {\eta '} \right) = {r_{ae,P}}\left( {\frac{{{r_{0P}}}}{{a{R_{{\mathop{\rm ref}\nolimits} }}}}\eta '} \right). $ | (15) |
由此,可以看出二维傅里叶变换前后的方位时间满足关系
| $ \eta = \frac{{{r_{0P}}}}{{a{R_{{\mathop{\rm ref}\nolimits} }}}}\eta '. $ | (16) |
式(13)和距离压缩后的信号式(6)形式完全一致,然而此时的合成孔径时间是一个由调制因子a控制的常数,距离r″PT′也不再是真实的平方开根号形式的距离r′PT′,而是和调制因子a和参考斜距Rref有关的量。CMBP算法通过方位调制巧妙地实现孔径的压缩从而减少BP算法的累加量,同时把方位空变误差的补偿嵌入到等效距离的计算中。
2.3 改进的FFBP算法本节首先介绍FFBP算法的原理,FFBP算法的核心思想是把距离压缩后的数据投影到中心距离线上。如图 2,中心距离线由子孔径中心点和子图像中心点确定,子孔径中心点坐标是相邻k(图 2中k=2)个航迹点坐标的中心,子图像中心点坐标是像素网格划分为M×N(图 2中M=N=2)个子图像后每个子图像的中心点。投影后的数据其孔径数量为原来的1/k,有效减少了计算量,上述过程可以递归进行以进一步减少计算量。在不递归时为LBP算法,按上述过程递归且因子为2时为QBP算法,每一次递归都可以设定任意因子的为FFBP算法,其中,QBP和FFBP算法的效率可以逼近频域算法。

|
Download:
|
| 图 2 中心距离线示意图 Fig. 2 Illustration of the center range beam | |
FFBP算法首先把距离压缩后的数据投影到中心距离线上。如图 2,以子孔径中心点为极点,以航迹方向为极轴正方向,则子图像所有点的极角都近似为中心距离线的极角,在中心距离线上设置一系列离散值ri,得
| ${R_i} = \sqrt {{t^2} + r_i^2 - 2t \cdot {r_i} \cdot \cos \theta } ,{r_i} = {r_c} + {i_r} \cdot \Delta r,\\ i = - \frac{N}{2}, - \frac{N}{2} + 1, \cdots ,\frac{N}{2} - 1. $ | (17) |
式中:rc=|PcT1|为子孔径中心点到子图像中心点的距离;t为子孔径中心点到原始航迹点的沿方位向的长度;N为中心距离线上数据的采样点数;Δr为中心距离线上的采样间隔,通常要满足距离向的奈奎斯特采样条件;极角θ满足
| $ \cos \theta = \frac{{{y_0} - {y_1}}}{{{r_0}}}. $ | (18) |
FFBP算法在极角上相当于利用邻近插值。
FFBP算法中的距离是真实地理距离,然而式(13)中的距离是通过式(14)定义的一种等效距离,CMFFBP算法是在改进的FFBP算法基础上实现的,式(14)中的vη等于当前航迹点到零多普勒点的距离,所以式(17)中的rc应由下式确定
| $ {r_c} = {r_0} - {R_{{\mathop{\rm ref}\nolimits} }} + \frac{{\Delta {y^2}}}{{2a{R_{{\mathop{\rm ref}\nolimits} }}}} + \frac{{{r_0}}}{{\sqrt {r_0^2 + \Delta {y^2}} }}{{r'}_{ae,{P_c}}}. $ | (19) |
其中,Δy=y0-y1。
由上,CMFFBP算法是CMBP和FFBP算法通过式(19)结合起来的一种算法。值得注意的是,式(17)中的θ依然由式(18)确定,因为FFBP算法是利用极角的最邻近插值实现局部近似从而提高算法效率,而等效距离不影响极角的物理概念,它只是在极径上进行了映射。换句话说,在斜距平面真实距离下极角相差Δθ,极径相差ΔR的两个点,映射为斜距平面等效距离下极角相差依然为Δθ,只是极径相差变为ΔR′,而FFBP算法其近似的来源在于极角,所以只要保持FFBP算法的极角的物理概念不变,其在等效距离下依然有效。
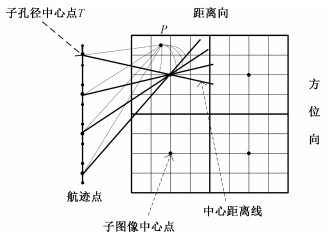
下面简要介绍LBP算法[4]以更好地理解CMFFBP算法。如图 3,对距离线上的任一点ri,在合并的孔径范围内每一个t,均可通过式(17)和式(19)得到Ri,根据Ri在相应的距离压缩后的数据插值,对这些插值结果在合并的k个航迹点中相干累加,从而把数据投影到中心距离线上,然后对像素网格任一点P,在其合成孔径范围内每一子孔径中心点T,根据|PT|在相应的中心距离向上插值出相应的值来,对这些值进行相干累加得到点P的成像值,对像素网格中的所有点进行上述过程得到最终的成像值。
|
Download:
|
| 图 3 LBP算法示意图 Fig. 3 Illustration of the LBP algorithm | |
QBP算法[5]和FFBP算法不同于LBP算法的地方在于其运用了递归的思想进一步减少其复杂度,LBP和QBP算法均可看作是FFBP算法的特殊情况,不再赘述。
2.4 非线性航迹及并行化分析2.3节介绍改进的FFBP算法时,没有考虑到航迹偏离带来的影响,本节分析式(7)中的方位空变误差rae, P(η)在FFBP算法中的补偿。在计算合并后的子孔径点时,其实在式(19)中已经考虑到方位空变误差的影响,设图 2中T1所处的二维傅里叶变换后的方位时间分别为η′1,则
| $ {{r'}_{ae,{P_c}}}\left( {{{\eta '}_1}} \right) = {r_{ae,{P_c}}}\left( {\frac{{{r_{0P}}}}{{a{R_{{\mathop{\rm ref}\nolimits} }}}}{{\eta '}_1}} \right). $ | (20) |
式(20)右边即为式(5)中的方位空变误差,可以通过插值得到。由此,方位空变误差得以补偿。上述过程可以递归进行,随着递归的进行,子孔径长度不断增加,其偏移量应该越大,但根据文献[6],其成像误差并不会随之增加,由此保证递归相对于非递归不会带来成像质量下降。
CMFFBP算法主要运算量集中在距离压缩后的数据投影到中心距离线以及对每一个像素点在中心距离线上进行插值和相干累加上,这部分的运算量可以通过并行得以减少。首先分析距离压缩后的数据投影到中心距离线部分,一方面不同的中心距离线没有先后关系,能够同时对多条中心距离线进行投影,另一方面每一条中心距离线上的一系列离散值ri对应的回波值的计算过程也没有先后关系,因此,把数据投影到中心距离线的这部分计算能够并行化。其次,对每个像素点在中心距离线上进行插值和相干累加这部分运算和原始BP算法的思想是一致的,容易通过并行实现。综上,CMFFBP算法易于并行化处理,可通过多核CPU或GPU进一步提高成像效率。
3 算法流程根据第2节算法原理的推导,CMFFBP算法流程如下:
1) 对接收到的回波进行解调和距离压缩,单点目标结果如式(1)所示(以下表达式均为单点目标情况);
2) 运用DMA对距离压缩后的信号运动误差的空不变分量和距离向空变分量进行补偿,补偿后的结果如式(6)所示,运动误差剩下方位向空变向量,为进一步提高精度,对DMA运动补偿后的信号进行方位重采样,以补偿沿方位向速度不均匀带来的误差;
3) 对DMA补偿和方位重采样后的信号进行二维傅里叶变换,参考函数相乘,Stolt插值,结果如式(10)所示;
4) 在二维频域对Stolt插值后的信号进行方位调制,调制后的信号如式(12)所示;
5) 对方位调制后的信号进行二维逆傅里叶变换,变换后的信号如式(13)所示;
6) 把等效距离压缩式(13)信号投影到中心距离线上,此时子孔径中心点和子图像中心点的距离根据式(19)计算,极角通过式(18)计算;
7) 对像素网格的每一像素点,根据该像素点到子孔径中心点的距离在中心距离线上插值,在合成孔径范围内对这些值进行相干累加,得到最终聚焦的图像。
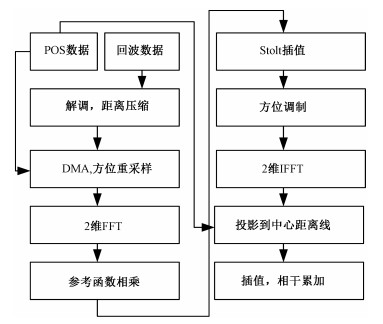
上述流程可用图 4表示,其中第3步为标准ωK算法中的处理步骤,第6步和第7步为FFBP算法步骤(此时利用的是等效距离),运动补偿体现或隐含在在第2步、第6步和第7步中。值得注意的是,流程中FFBP算法特指LBP算法,一般的FFBP算法可以在此基础上递归形成新的中心距离线。
|
Download:
|
| 图 4 CMFFBP算法流程图 Fig. 4 Flow chart of the CMFFBP algorithm | |
为验证所提算法的有效性,选择一个由中国科学院电子学研究所研制的C波段机载SAR系统进行相关实验,主要参数如表 1所示。为便于比较,设计点目标仿真实验和实测数据实验,分别利用CMBP、FFBP和CMFFBP算法进行实验,并对成像质量和成像效率进行比较分析。
|
|
表 1 SAR主要参数 Table 1 The main parameters of SAR system |
为使仿真结果最大程度地接近实测结果,仿真使用的航迹为真实SAR飞行航迹,其在2 500 m的飞行距离中沿x正负方向相对于理想航迹的最大偏离量分别为0.44和-0.35 m,沿z正负方向相对于理想航迹的最大偏离为0.18和-0.22 m,其航迹偏离量如图 5所示。用3种算法,即CMBP、FFBP。和CMFFBP算法对仿真的回波进行处理,算法运行在Microsoft Visual Studio 2008平台下。为便于衡量成像质量,成像过程中方位向和距离向所加的窗均为矩形窗,设置9个点目标,位置如图 6所示。通过对成像的结果进行点目标分析,可以定量计算点目标的冲激响应宽度(impulse response width,IRW),峰值旁瓣比(peak sidelobe rate,PSLR),积分旁瓣比(integration sidelobe rate,ISLR)和运行时间,从而比较各个算法的效率和精度,仿真参数中式(12)的方位调制系数a=0.1,成像区域大小为4 096像素×4 096像素。

|
Download:
|
| 图 5 SAR飞行沿方位向的偏离 Fig. 5 SAR deviations along the x-and z-directions | |

|
Download:
|
| 图 6 点目标分布示意图 Fig. 6 Distribution of point targets | |
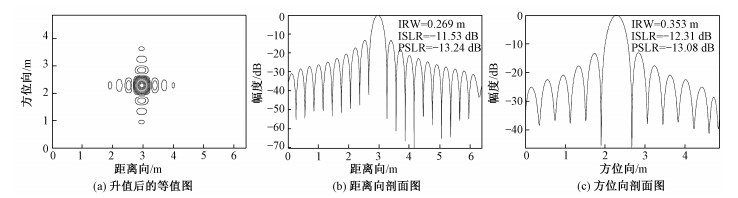
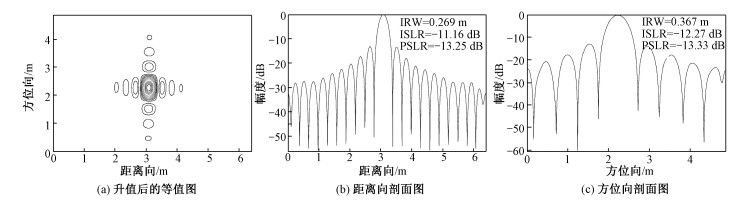
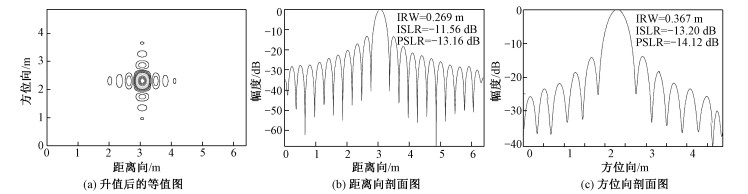
点目标成像幅度图如图 7所示,可以看出9个点目标均已聚焦成像,从9个点中选择图 6的A点,对其周围的32×32邻域进行二维sinc升采样,升采样倍数为32。CMBP、FFBP和CMFFBP算法升采样的等值线、距离向剖面图和方位向剖面图分别如图 8~图 10所示,从中可以看出3种算法的成像结果均几乎呈理想的二维sinc信号。进一步的定量表明,CMBP、FFBP和CMFFBP算法的距离向IRW分别为0.269、0.269和0.269 m,和理想值(表 1中SAR参数距离向分辨率)0.266 m几乎完全一致;方位向IRW分别为0.353、0.376和0.367 m,和理想值0.336 m也基本一致。CMBP、FFBP和CMFFBP算法的距离向峰值旁瓣比分别为-13.24、-13.25和-13.16 dB,和理想值-13.26 dB(矩形窗的理论值)几乎完全一致;方位向峰值旁瓣比分别为-13.08、-13.33和-14.12 dB,和理想值-13.26 dB也基本一致。同时,可以发现,3种算法的成像质量基本一致。为更进一步评估点目标成像质量,选择图 6中的A、B、C、D和E5个点目标在3种算法下的IRW、PSLR和ISLR值分别列在表 2~表 4中,从这3个表可以看出,3种算法成像质量均逼近理想点目标,因此,CMFFBP算法相对于另外两种算法在精度上的损失基本可以忽略。

|
Download:
|
| 图 7 点目标成像结果 Fig. 7 The imaging results of point targets | |
|
Download:
|
| 图 8 CMBP算法点目标分析 Fig. 8 The point target analysis of the CMBP algorithm | |
|
Download:
|
| 图 9 FFBP算法点目标分析 Fig. 9 The point target analysis of the FFBP algorithm | |
|
Download:
|
| 图 10 CMFFBP算法点目标分析 Fig. 10 The point target analysis of CMFFBP algorithm | |
|
|
表 2 CMBP算法的点目标成像质量参数 Table 2 The point target quality parameters of CMBP algorithm |
|
|
表 3 FFBP算法的点目标成像质量参数 Table 3 The point target quality parameters of the FFBP algorithm |
|
|
表 4 CMFFBP算法的点目标成像质量参数 Table 4 The point target quality parameters of the CMFFBP algorithm |
在a=0.1时,CMBP、FFBP和CMFFBP算法的运行时间分别为7.059、11.655和3.701 min,可以看出,CMFFBP算法相对于CMBP算法提高47.6%,相对于FFBP算法提高68.2%。为进一步比较3种算法的效率,计录不同的a值下3种算法的运行时间,如表 5和图 11所示,可以看出,当a比较小(如a=0.01)时,CMBP和CMFFBP运行时间基本一致,随着a值的增大,CMBP和CMFFBP算法的运行时间随a的增加呈近似线性关系,但是CMBP算法的斜率比较大,说明CMFFBP算法的效率比CMBP高,随a的增加,效率提高得越显著;从图 11还可看出,当a小于0.78时,CMFFBP算法比CMBP和FFBPN算法的效率高,当a接近1时,由于此时方位调制并未明显减少等效合成孔径长度,CMFFBP算法由于前期的ωK预处理,会比FFBP算法稍微多运行一点时间。总的来说,CMFFBP算法在a<0.4时相对于CMBP和FFBP算法,效率明显提高。
|
|
表 5 不同参数a下的CMBP,FFBP和CMFFBP算法的运行时间 Table 5 Running time of the CMBP, FFBP, and CMFFBP algorithms at different a values |

|
Download:
|
| 图 11 CMBP,FFBP和CMFFBP算法的运行时间随a增加的变化图 Fig. 11 Running time of the CMBP, FFBP, and CMFFBP algorithms vs. the a parameter | |
综上,仿真结果表明,CMFFBP算法相对于CMBP和FFBP算法在几乎没有损失精度的情况下,显著提高成像效率。
4.2 实测实验结果与分析利用实测SAR数据验证所提算法的有效性,SAR参数如表 1所示,航迹偏离量如图 5所示,测试数据大小为4 096像素×4 096像素,a=0.01。3种成像算法的成像结果如图 12所示,可以看出,三者均能对场景清晰成像。为进一步比较三者的成像质量,对图 12中白色矩形框区域进行放大显示,如图 13所示,可以看到,其聚焦质量良好,三个算法的成像质量基本一致,所以,CMFFBP算法相对于CMBP和FFBP算法在成像精度上没有明显损失。在成像效率上,CMBP、FFBP和CMFFBP算法的运行时间分别为3.806、12.219和2.98 min,和表 5中a=0.01基本吻合,因此,CMFFBP算法的效率优于另外两种快速BP算法。

|
Download:
|
| 图 12 CMBP, FFBP和CMFFBP成像结果 Fig. 12 The imaging results of CMBP, FFBP, and CMFFBP algorithms | |

|
Download:
|
| 图 13 图 12白色矩形框区域的放大图 Fig. 13 Enlarged views of the three white rectangular areas in Fig. 12 | |
综上,实测数据实验表明,所提算法能对实测数据进行高质量聚焦,其成像质量和CMBP以及FFBP算法几乎相同,表明其在提高成像效率的同时并未对成像质量造成明显影响,至此,通过仿真和实测数据验证了所提算法的有效性,其在精度和效率均能取得令人满意的效果。
5 总结本文从两类快速BP算法入手,设法使得两类快速算法的优势结合起来,进一步提高算法的运行效率,其中CMBP算法利用方位调制技术实现孔径的压缩,使得等效合成孔径长度按给定因子压缩,相当于使合成孔径长度变短,从而减少运算量;FFBP算法通过引入中心距离线的概念把相邻孔径合并,相当于减少合成孔径范围内的孔径点数;而CMFFBP算法把上述二者结合起来,一方面减少合成孔径长度,另一方面减少合成孔径范围内孔径点数量,从而进一步减少计算量,值得注意的是,FFBP算法能够通过递归实现,所以CMFFBP算法也能够利用递归进一步减少计算量,本文没有对此展开。通过仿真和实测数据实验,所提算法相对于CMBP和FFBP算法其成像质量几乎没有下降,而效率明显提高,验证了该算法的有效性。
| [1] |
韩冰, 张永军, 刘佳音, 等. 斜视滑动聚束SAR成像的ECS算法[J]. 中国科学院研究生院学报, 2012, 29(5): 674-680. |
| [2] |
张升康, 杨汝良. 双基地合成孔径雷达扩展Chirp Scaling成像算法[J]. 中国科学院研究生院学报, 2008, 25(1): 101-109. |
| [3] |
Munson D C J, O'Brien J D, Jenkins W. A tomographic formulation of spotlight-mode synthetic aperture radar[J]. Proceedings of the IEEE, 1983, 71(8): 917-925. |
| [4] |
Yegulalp A F. Fast backprojection algorithm for synthetic aperture radar[C]//Proceedings of the 1999 IEEE Radar Conference, Waltham, 1999: 60-65. http://ieeexplore.ieee.org/iel5/6212/16591/00767270.pdf
|
| [5] |
Oh S M, Mcclellan J H. Multiresolution imaging with quadtree backprojection[C]//35th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 2001: 105-109. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=986888
|
| [6] |
Ulander L M H, Hellsten H, Stenstrom G. Synthetic-aperture radar processing using fast factorized back-projection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 760-776. |
| [7] |
Meng D, Hu D, Ding C. Precise focusing of airborne SAR data with wide apertures large trajectory deviations:a chirp modulated back-projection approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2510-2519. |
| [8] |
Meng D, Ding C, Hu D, et al. On the processing of very high resolution spaceborne SAR data:a chirp-modulated back projection approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 99: 1-11. |
| [9] |
Meng D, Hu D, Ding C. A new approach to airborne high resolution SAR motion compensation for large trajectory deviations[J]. Chinese Journal of Electronic, 2012(4): 764-769. |
| [10] |
Macedo K A C D, Scheiber R. Precise topography- and aperture-dependent motion compensation for airborne SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 172-176. |
| [11] |
Prats P, Reigber A, Mallorqui J J. Topography-dependent motion compensation for repeat-pass interferometric SAR systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(2): 206-210. |
| [12] |
Zheng X, Yu W, Li Z. Motion compensation for wide beam SAR based on frequency division[J]. Journal of Electronics, 2008, 25(5): 607-615. |
 2018, Vol. 35
2018, Vol. 35 


