2. 中国科学院地球科学研究院, 北京 100029;
3. 中国科学院大学, 北京 100049;
4. 中南大学地球科学与信息物理学院, 长沙 410083
2. Institutions of Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. School of Geoscience and Info-Physics, Central South University, Changsha 410083, China
地下水资源在保障社会经济发展和维持生态平衡中扮演着不可或缺的角色[1]。然而,由于盲目开发或保护不当造成的地下水污染问题日益严重[2]。为遏制地下水污染态势进一步恶化,需要采取有效措施保护地下水安全或进行地下水污染治理,而开展这些工作的前提之一是全面了解地下水质量状况[3]。目前查明地下水质量现状的方法可划分为直接方法和间接方法。直接方法通过进行水文地质钻探、建立监测井获取地下水样品进行成分分析。该方法虽然准确性高,但是样本具有局限性且成本较高。间接方法则主要是通过地球物理手段查明相应的物理场(电场,磁场等)分布状态,根据物理场异常的特征推测地下水质量状况[4-7]。但是地球物理方法存在多解性的问题,这会造成对异常信息进行分析时所推测的结果可能不符合实际[8]。因此,应用地球物理方法探查地下水污染的关键是构建准确、可靠的地球物理信息与污染物浓度之间的映射关系。目前,国内外在此方面的研究并无成熟的方法,多数为直接利用Archie经验公式将视电阻率反演数据转换为地下水污染物浓度数据[9],但受限于Archie公式适用范围,采用这种方式所估算的结果误差较大。此外,一些学者通过电阻率成像技术(ERT,electrical resistance tomography)、数值实验以及盐示踪实验来研究视电阻率反演数据与浓度之间的关系[10-13]。
针对电阻率信息向污染物浓度信息转换困难的问题,本文参考Singha和Moysey[8]提出的方法尝试基于地下水流动与溶质运移模拟和地球物理正反演模拟来获取含水层的电阻率数据与污染物浓度数据,并通过不同的统计方法构建其映射关系,从而达到通过视电阻率反演数据估计地下水污染物浓度的目的,其中本文将Singha所提方法中的线性拟合改进为多项式拟合。研究结果显示该方法所估算的地下水污染物浓度相比于直接应用Archie公式能够更加准确地获取整体场域信息,同时多项式拟合建立的映射关系估算的结果是最佳的,所以合理地运用该方法将可成为钻孔直接取样监测方法的有力补充。
1 研究方法与模型实例 1.1 研究方法地电勘探中在野外获取到的观测数据为视电阻率数据,对观测数据反演计算后可推断地下物性结构。但是直接通过视电阻率反演剖面推断出地下水污染物浓度及范围难度大且不精确。而本研究通过建立视电阻率与污染物浓度的映射关系,应用该映射关系可实现对地下水污染物浓度的定量估计。
研究方法归结为以下几个步骤:1)通过建立理想的地下水水流和溶质运移模型模拟计算获取地下水溶质参考浓度场,该参考浓度场相当于实际中存在的未知地下溶质的浓度场,而亟待解决的问题即是估计该浓度场的浓度。2)利用该浓度场的浓度数据建立地电模型进行正演计算得到类似于实际野外观测数据。3)将获取到的“观测数据”进行反演计算得到视电阻率反演数据。4)通过统计拟合的方法建立视电阻率反演数据和浓度场的浓度映射关系。5)应用该映射关系根据视电阻率反演数据推算出一个估计的浓度场。通过对比参考浓度场和估计的浓度场,分析该映射关系的可靠性。
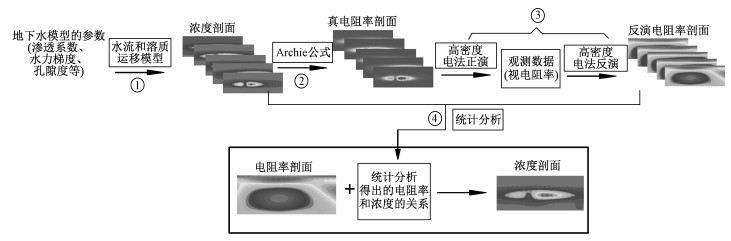
本文所建立的浓度和反演电阻率的映射关系并非一个经验公式,而是一种随空间变化的关系。具体步骤如下(图 1):
|
Download:
|
| 图 1 建立浓度和电阻率映射关系的流程图 Fig. 1 Flowchart of establishing the relationship between concentration and electrical resistivit | |
1) 浓度场数据的获取:假定地下水在含水层中的运动满足达西定律,据此可得地下水渗流连续性方程[14]:
| $ \nabla \cdot (K\nabla h)={{S}_{S}}\frac{\partial h}{\partial t}+W, $ | (1) |
式(1)描述地下水在多孔介质中的三维非稳定运动,其中:K为渗透系数,h为水头高度,SS为储水率,t为时间,W为单位体积的源汇项。假定溶质在地下水中的迁移满足菲克定律,可用如下对流弥散方程[15]描述:
| $ \frac{{\partial c}}{{\partial t}} = \nabla \cdot{\rm{ }}(\mathit{\boldsymbol{D}}\nabla c) + \nabla \left( {\mathit{\boldsymbol{\mu }}c} \right), $ | (2) |
式中:c为溶液中某种组分的浓度,μ为实际平均流速矢量,D为水动力弥散系数。联立上述的两个方程即可获取溶质随地下水迁移的时空分布数据。为了获取多个浓度场数据以建立映射关系并进行统计检验,研究中利用随机方法建立多个渗透结构作为模型输入。
2) 电阻率数据的获取:电阻率为电导率的倒数,而电导率与溶质浓度呈相关性。模型模拟的浓度值在每一个网格中均代表其局部值,恰好能够利用“局部适用”的Archie经验公式[9]直接将浓度转换为电阻率:
| $ {\rho _b} = F \cdot {\rho _f}, $ | (3) |
式中:ρb为电阻率(Ω·m);ρf为溶液电阻率(Ω·m); F为转换参数(无量纲)。
3) 地球物理正反演模拟:地球物理正演是指由源的属性导出到地球物理场的分布属性;反演则是正演的逆过程,是由地球物理场的分布来推导源的属性。利用Archie公式转换而来的电阻率数据进行地球物理正演模拟,便可获取类似于野外地球物理勘探工作中所观测到的电阻率数据,再对正演数据进行反演,获取视电阻率反演数据。
4) 映射关系的建立:统计出不同模型中相应网格的浓度数据与视电阻率反演电阻数据,利用线性拟合和多项式拟合针对每个网格中的浓度数据和视电阻率反演数据进行拟合。
5) 应用上述建立的映射关系根据视电阻率反演数据推算出估计的浓度场,将估计的浓度场和参考浓度场进行对比,从不同角度分析该视电阻率反演数据和参考浓度数据映射关系的可靠性及该方法的可行性。
1.2 建立映射关系实例联合MODFLOW[16]与MT3DS[17]建立一个二维地下水流动与溶质运移模型:模型长200 m,深(高)45 m,采用1 m×1 m矩形网格对模拟区进行剖分;水流采用稳定流模拟计算,溶质运移模拟期为20 d;模型两侧均为定水头边界,水力梯度设置为0.000 1,全场初始质量浓度为50 mg/L。通过改变渗透结构输入获取50个不同渗流场的地下水模型。不同渗透系数通过50次随机实现,随机过程平均值为117 m/d,标准差为1.58。在所获取的50个渗流场投入点源污染物,污染源质量浓度为2 500 mg/L,最后获取50个不同的浓度场分布。利用浓度值与电导率之间存在换算关系[9](1 mg/L=2 μS/cm)与Archie公式将浓度场分布转换为电阻率场分布,本文中参数F取5[9]。
研究中采用高密度电阻率法进行地球物理正、反演计算,采用的软件为Res2dmod与Res2dinv,该软件是由M.H.Loke基于二维有限差分法和二维有限元方法开发的一套公认的高密度电阻率数据二维正、反演软件[18]。正演计算过程中建立一个长200 m,深(高)45 m的地电模型,由于Res2dmod在剖分上不能将每一层的深度设置成相同参数,故仅在模型的敏感区(深度在0~15 m)的剖分与地下水模型中的剖分一致,即在模型0~15 m之间采取1 m×1 m网格剖分,其余区域的剖分依次增大;水平剖分方面将电极距设置为1 m即可,完成模型的剖分之后,在不同的网格中赋以由相应浓度换算的电阻率值。正演计算之后利用Res2div针对正演计算的数据进行反演计算得到视电阻率反演数据。
最后,统计分析浓度数据和视电阻率反演数据,采用不同拟合方式拟合浓度值与视电阻率反演数据之间的关系,进而确定二者映射关系。
2 不同拟合方式的应用结果分析本研究一共分析5个不同渗透系数的模型进行不同拟合方式的应用结果。发现5个模型中有4个模型的应用结果相似,故在这4个模型中选取模型1代表该4个模型的应用结果,剩余的一个模型(模型2)的应用结果与其余4个有明显的差异。所以本文只讨论模型1和模型2的应用结果,其中模型1的渗透系数为75 m/d,模型2的渗透系数为28 m/d。
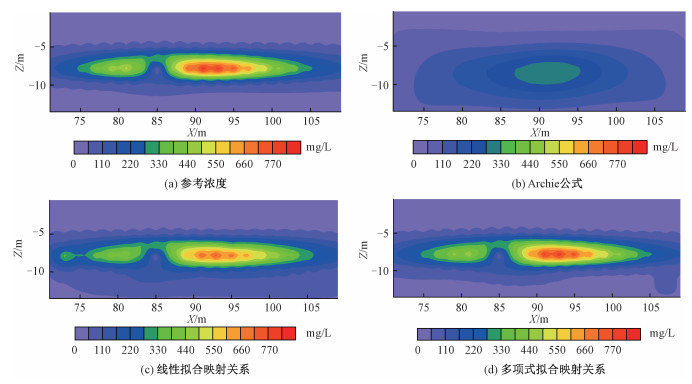
2.1 模型1不同拟合方式的应用结果分析将MT3DMS模拟的浓度场作为参考浓度场(图 2(a)),Archie公式估算的浓度场(图 2(b))、线性拟合建立的映射关系估算的浓度场(图 2(c))以及多项式拟合建立的映射关系估算的浓度场(图 2(d))进行对比发现:对于污染晕形态的刻画,Archie公式估算的浓度场中,污染晕呈现一个椭圆的形态,与参考浓度场差异明显;线性拟合和多项式拟合建立的映射关系的应用结果均十分接近参考浓度场,显著优于直接应用Archie公式,但是二者的差别不明显。因此,对于污染晕的刻画,线性拟合与多项式拟合建立的映射关系估算的结果要显著优于Archie公式估算的结果。
|
Download:
|
| 图 2 模型1利用不同方式得到的浓度剖面图 Fig. 2 The concentration maps of model 1 produced using different ways | |
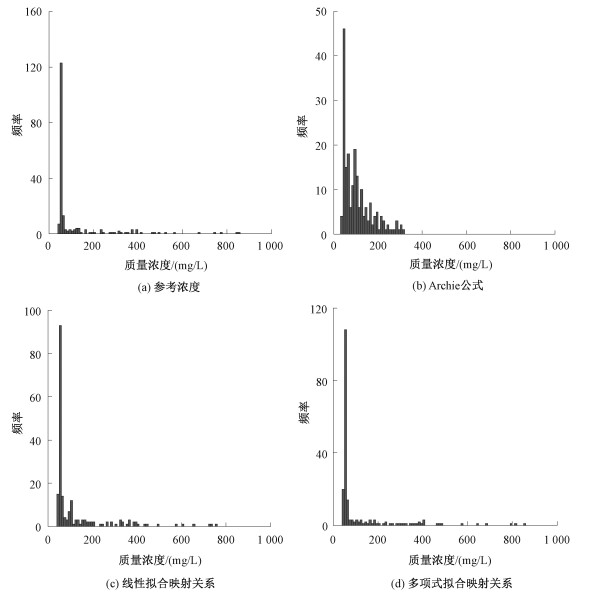
对浓度值进行频率统计:参考浓度场质量浓度多集中在0~100 mg/L(图 3(a)),存在高浓度值;Archie公式估算的质量浓度分布(图 3(b))集中在0~350 mg/L,未出现较高的浓度值(>400 mg/L),这与参考浓度场明显不同。线性拟合建立的映射关系估算的浓度分布(图 3(c))与多项式拟合建立的映射关系估算的浓度分布(图 3(d))均接近于参考浓度剖面浓度分布,主要集中在0~100 mg/L,也存在高浓度值。因此对于浓度分布而言,线性拟合与多项式拟合所建立的映射关系估算效果优于直接利用Archie公式。
|
Download:
|
| 图 3 模型1利用不同方式得到的浓度剖面的浓度分布柱状图 Fig. 3 The concentration distribution histogram of concentration maps of model 1 produced using different ways | |
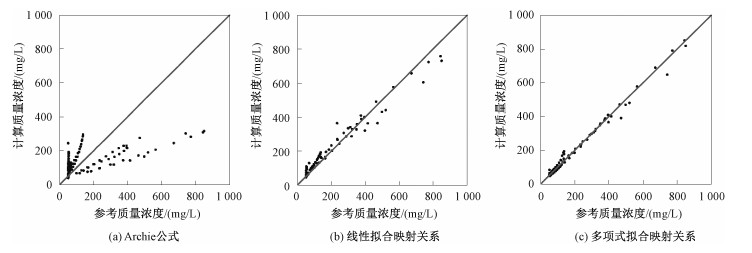
为进一步评估不同方法估算的污染物浓度值的可靠性,可将参考浓度作为横坐标、计算浓度值作为纵坐标,评估散点是否分布在对角线附近,越靠近对角线说明二者越相似,表明该方法越可靠。Archie公式估算的散点偏离对角线,并表现出低浓度散点位于对角线上方,高浓度散点位于对角线下方,即在低浓度区域会高估浓度值,在高浓度区域会低估浓度值(图 4(a));利用线性拟合建立的映射关系和多项式拟合建立的映射关系估算的浓度均集中分布在对角线附近(图 4(b),4(c)),表明两种映射关系估算的每个网格的浓度值都接近于参考浓度值。
|
Download:
|
| 图 4 模型1不同方式计算的浓度与参考浓度散点图 Fig. 4 The scatter plot of the reference concentration and the concentration produced using different ways | |
综上,在模型1中应用Archie公式法、线性拟合建立的映射关系及多项式拟合建立的映射关系分别估算地下水溶质浓度值,结果表明,线性拟合与多项式拟合建立的映射关系估算效果明显优于Archie公式法估算效果。
2.2 模型2不同拟合方式的应用结果分析将模型2的参考浓度场(图 5(a))与Archie公式估算的浓度场(图 5(b))、线性拟合建立的映射关系估算的浓度场(图 5(c))以及多项式拟合建立的映射关系估算的浓度场(图 5(d))进行对比发现:对于污染晕形态的刻画,Archie公式估算的浓度场中污染晕的形态与参考浓度场差异明显;线性拟合建立映射关系估算的污染晕形态虽然比起Archie公式要接近于参考浓度场,但在低浓度区域出现负值,这是由于假定场域中所有的点都符合同一个线性函数来建立映射关系所引起;多项式拟合建立的映射关系的应用结果解决线性拟合中出现负值的问题,也更接近于参考浓度场。因此对于污染晕的刻画方面,多项式拟合建立的映射关系要优于线性拟合建立的映射关系和直接应用Archie公式。

|
Download:
|
| 图 5 模型2利用不同方式得到的浓度剖面图 Fig. 5 The concentration maps of model 2 produced using different ways | |
对浓度值进行频率统计:参考浓度场质量浓度多集中在0~100 mg/L(图 6(a)),同样存在高浓度值;Archie公式估算的质量浓度分布(图 6(b))在0~200 mg/L,未出现较高的浓度值(>400 mg/L),这与参考浓度场明显不符;线性拟合建立的映射关系估算的质量浓度分布(图 6(c))主要集中在0~100 mg/L,也存在高浓度值,但出现负浓度值的分布。多项式拟合建立的映射关系估算的浓度分布(图 6(d))更为接近于参考浓度剖面浓度分布,主要集中在0~100 mg/L,不存在负浓度值。因此进一步可以发现,线性拟合建立的映射关系在模型2上的应用是存在问题的,多项式拟合建立的映射关系要优于线性拟合建立的映射关系和直接应用Archie公式。

|
Download:
|
| 图 6 模型2利用不同方式得到的浓度剖面的浓度分布柱状图 Fig. 6 The concentration distribution histogram of concentration maps of model 2 produced using different ways | |
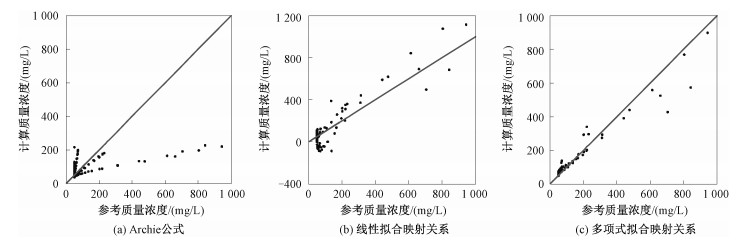
同样将参考浓度作为横坐标、计算浓度值作为纵坐标,评估不同方法估算的污染物浓度值的可靠性。Archie公式估算的浓度仍然不准确,散点明显地偏离对角线(图 7(a));线性拟合建立的映射关系的散点(图 7(b))在低浓度部分出现异常,不集中分布于对角线;多项式拟合建立的映射关系的散点(图 7(c))更为集中对角线附近,即其估计的浓度值会更加接近于参考浓度值。
|
Download:
|
| 图 7 模型2不同方式计算浓度与参考浓度对比关系 Fig. 7 The scatter plot of the reference concentration and the concentration produced using different ways | |
综上,在模型2中应用Archie公式法、线性拟合建立的映射关系及多项式拟合建立的映射关系分别估算地下水溶质浓度值,结果表明,多项式拟合建立的映射关系估算效果明显优于线性拟合建立的映射关系估算效果的与Archie公式法估算效果。
3 结论与展望1) 联合地下水数值模拟与电阻率成像法建立地下水污染物浓度和电阻率之间的映射关系是可行的。利用所建立的映射关系,可从视电阻率反演剖面估计出地下水污染物的浓度,这较直接应用Archie公式有显著的改善,因此可作为钻井取样直接监测的有力补充。
2) 地下污染物浓度和电阻率的映射关系具有空间特征,表现在每个网格中对应的映射关系都不相同;利用线性拟合和多项式拟合建立的映射关系在大多数模型上的应用效果差异不大,但都优于直接应用Archie公式计算的结果;对于某些特殊的模型(如模型2),利用线性拟合映射关系所计算的结果会出现负值,因此,其应用效果要劣于多项式拟合映射关系计算的效果。
3) 很多因素都直接影响本文所提方法的准确性,包括地下水数值模型的准确性、Archie公式中的转换参数、电阻率数据的准确性等。此外本文提出的方法还处于研究的初步阶段,文章中所建立的地下水数值模型是理想模型,有别于实际的地下水运动与溶质迁移特征,因此需要在实际的场域中进行应用,进一步确定该方法的适用性。
| [1] |
熊玲, 鄢贵权. 浅谈我国地下水的污染现状及防治措施[J]. 贵州科学, 2009, 27(4): 86-90. DOI:10.3969/j.issn.1003-6563.2009.04.014 |
| [2] |
郭永海, 王志明, 刘淑芬, 等. 石家庄市地下水污染特征及其与超量开采的关系[J]. 铀矿地质, 2005, 21(2): 123-127. DOI:10.3969/j.issn.1000-0658.2005.02.010 |
| [3] |
王爱平, 杨建青, 杨桂莲, 等. 我国地下水监测现状分析与展望[J]. 水文, 2010, 30(6): 53-56. DOI:10.3969/j.issn.1000-0852.2010.06.013 |
| [4] |
钟秋. 地下水污染调查中的地球物理方法[J]. 地下水, 2014, 36(2): 57-58. DOI:10.3969/j.issn.1004-1184.2014.02.023 |
| [5] |
喻永祥, 吴吉春. 利用ERT数据推求非均质多孔介质渗透系数初探[J]. 水文地质工程地质, 2006, 33(2): 41-44. DOI:10.3969/j.issn.1000-3665.2006.02.010 |
| [6] |
闫永利, 马晓冰, 袁国平, 等. 大地电磁法在阿苏卫填埋场地下水污染检测的应用研究[J]. 地球物理学报, 2007, 50(6): 1863-1868. DOI:10.3321/j.issn:0001-5733.2007.06.029 |
| [7] |
杨学明, 苏永军, 杜东, 等. 音频大地电磁法在海水入侵动态监测中的应用[J]. 物探与化探, 2013, 37(2): 301-305. |
| [8] |
Singha K, Moysey S. Accounting for spatially variable resolution in electrical resistivity tomography through field-scale rock-physics relations[J]. Geophysics, 2006, 71(4): A25. DOI:10.1190/1.2209753 |
| [9] |
Singha K, Gorelick S M. Hydrogeophysical tracking of three-dimensional tracer migration:the concept and application of apparent petrophysical relations[J]. Water Resources Research, 2006, 42(6): 253-263. |
| [10] |
Koestel J, Kemna A, Javaux M, et al. Quantitative imaging of solute transport in an unsaturated and undisturbed soil monolith with 3-D ERT and TDR[J]. Water Resources Research, 2008, 44(12): 1-17. |
| [11] |
Pollock D, Cirpka O A. Temporal moments in geoelectrical monitoring of salt tracer experiments[J]. Water Resources Research, 2008, 44(12): 723-729. |
| [12] |
Wehrer M, Slater L D. Characterization of water content dynamics and tracer breakthrough by 3-D electrical resistivity tomography (ERT) under transient unsaturated conditions[J]. Water Resources Research, 2015, 51(1): 97-124. DOI:10.1002/2014WR016131 |
| [13] |
李国山, 周启友, 刘汉乐, 等. 高密度电阻率成像法监测静水中溶质运移过程[J]. 工程勘察, 2008(10): 72-75. |
| [14] |
张嘉, 王明玉. 非均质渗透介质纵向弥散度数值模拟估算法适宜性探析[J]. 中国科学院研究生院学报, 2011, 28(1): 35-42. |
| [15] |
薛禹群. 地下水数值模拟[M]. 北京: 科学出版社, 2007.
|
| [16] |
Harbaugh A W. MODFLOW-2005, the US Geological survey modular ground-water model:the ground-water flow process[M]. Reston: US Department of the Interior, US Geological Survey, 2005.
|
| [17] |
Ma R, Zheng C M. Effects of density and viscosity in modeling heat as a groundwater tracer[J]. Groundwater, 2010, 48(3): 380-389. |
| [18] |
施庆国.高密度电阻率法二维和三维有限差分正演计算[D].长春: 吉林大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10183-1012366666.htm
|
 2018, Vol. 35
2018, Vol. 35 


