2. 中国科学院大学, 北京 100049;
3. 中国人民解放军62026部队, 西安 710032
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. 62026 PLA Troops, Xi'an 710032, China
建筑物的SAR图像仿真技术是根据建筑物的三维模型和雷达的成像参数,仿真电磁波在目标场景中的散射作用,生成逼真的SAR图像的过程[1]。仿真SAR图像与真实SAR图像在几何特征和辐射特征方面保持一定的一致性[2]。通过改变目标模型和成像参数,即可简单高效地预测出多角度、不同分辨率的SAR图像,为建筑物的分类、识别及三维重建等研究提供大量的SAR图像。因此对SAR图像仿真技术的研究具有重要的现实意义。
根据后向散射模型和模拟技术的不同,仿真方法可分为两种[3]。一种是模拟SAR原始回波信号的仿真方法。Franceschett等[4-6]通过物理光学(PO)[7]和几何光学(GO)[8]理论近似电磁波在目标表面的散射过程,得到回波信号;Xu和Jin[9]采用积分方程模型(IEM)计算电磁散射矩阵,获得回波信号;Delliere等[10]提出时域有限差分模型(FDTD)近似电磁波的后向散射过程以得到回波信号。这种仿真方法计算复杂,且仿真精度的提高强烈依赖目标建模精度,对建筑物中不可忽视的多次散射难以计算。另一种方法是基于几何特征的仿真方法,通过直接建立目标场景与二维SAR图像间的几何映射关系得到SAR仿真图像。Stefan[11]设计的RaySAR仿真器用Phong Shading模型计算散射强度。Balz和Stilla[12]提出的SARVIZ仿真器用光栅法计算几何映射关系。Bolter[13]提出针对建筑物几何特征的仿真方法,并且对图像几何畸变和斑点噪声的特性进行深入研究。建筑物的外墙、窗户等部件易形成二、三面角结构,在SAR图像中形成明显的几何特征[14-16]。基于特征的仿真方法不仅能够简洁高效地实现对SAR图像特征的仿真,还能建立目标空间结构与图像散射现象之间的对应关系,成为近年来的研究热点[17-18]。
本文介绍一种基于图像几何特征的高分辨率SAR图像仿真方法。该方法首先由3D模型和雷达参数构建成像几何模型;其次,通过改进光学着色模型计算电磁波的散射特性;然后根据SAR成像原理改写Pov-Ray(persistence of vision ray),在雷达与场景间展开射线追踪,建立三维场景与二维图像之间的映射关系,得到电磁波在场景中的散射点的位置、强度等信息;根据强度和位置进行二维成像,形成初步的SAR图像强度图;最后,对强度图进行系统卷积、添加噪声、插值等后处理过程,得到逼真的仿真SAR图像。
1 仿真模型 1.1 成像几何模型成像几何模型在同一坐标系中描述SAR图像仿真中虚拟雷达的位置以及三维目标的几何位置。SAR系统采用主动侧视斜距成像模型,传感器在同一位置发射和接收电磁波。在同一场景范围内,雷达的航向和飞行高度不变。在远场的条件下,认为雷达在局部场景范围内以平行波入射,射线与水平面夹角均为θ。建立局部直角坐标系,如图 1所示。

|
Download:
|
| 图 1 成像场景模型 Fig. 1 Model of imaging scene | |
以雷达飞行方向为Y轴(方位向),水平面内垂直于飞行方向的为X轴(距离向),高度向为Z轴。电磁波由虚拟雷达S发出,经路径r1与目标场景产生第一个交点P1,若电磁波直接反射回接收传感器,此时产生一次散射回波;若电磁波在P1发生镜面反射,经路径r12到达建筑物表面P2,再由路径r2到达接收器,则此时产生二次散射。
在传感器发射电磁波进行采样时,同一方位向的采样线数目n应满足n≥Xsinθ/ΔR,其中X表示距离向场景范围,ΔR表示距离向分辨率,取等号时,每个分辨单元有一个采样点。图像仿真中,可以根据需求增加每个分辨单元的采样点数,即增加每个单元的散射点数目,提高图像精度。在射线追踪的过程中,假设每条采样线照射在一个散射点内,相邻的分辨单元没有叠加。后续将得到的散射强度图与点扩散函数进行卷积处理,以接近雷达电磁波带宽有限的事实。
1.2 散射模型由散射模型可以得到仿真SAR图像的强度。本文采用改进的光学着色模型Phong Shading作为电磁散射模型。在Phong Shading模型中,各点的光学着色通过顶点插值计算,逼真度较高,光强由环境光、镜面反射和漫反射光构成。在SAR成像中,雷达接收到环境散射的电磁波忽略不计,即对目标表面的漫反射只计算一次,不追踪漫反射的多次反射。在SAR图像仿真中,电磁波在目标表面的散射特性由镜面反射和朗伯体散射两部分近似,镜面反射和朗伯体散射强度的和值代表图像灰度大小。两种散射的计算公式为:
| $ {I_{\rm{d}}} = {k_{\rm{d}}}{I_{{\rm{in}}}}\left( {\mathit{\boldsymbol{N}} \cdot \mathit{\boldsymbol{L}}} \right), $ | (1) |
| $ {I_{\rm{s}}} = {p_i}{k_{\rm{s}}}{\left( {\mathit{\boldsymbol{N}} \cdot \mathit{\boldsymbol{H}}} \right)^n}. $ | (2) |
式中:Id表示漫反射能量强度;kd表示漫反射系数,取值在(0, 1)之间;Iin表示一个分辨单元内信号的入射强度;L表示入射向量;N是入射平面的法向量;Is表示目标表面发生的镜面反射强度;H是入射向量与视点方向的半角向量,发生镜面反射时,H与N重合;ks表示镜面反射系数,取值在(0, 1)之间;n是反射光的空间分布因子,n值越大,目标表面的散射空间分布越集中;pi是控制因子,随着镜面反射次数i的增加,pi减小,当i达到设定的最大镜面反射追踪次数(本文i最大值为5)时,pi为0,认为反射回波能量太弱不能被接收到。当回波向量与镜面反射向量之间的夹角Δα小于1°时,认为发生的散射都是镜面散射。镜面散射中,反射向量S的计算公式为
| $ \mathit{\boldsymbol{S}}{\rm{ = }}\mathit{\boldsymbol{R}}{\rm{ - 2}}\mathit{\boldsymbol{N}} \cdot \left( {\mathit{\boldsymbol{N}} \cdot \mathit{\boldsymbol{R}}} \right). $ | (3) |
式中:S表示反射向量,R表示由天线指向目标表面交点P方向的初始射线。
1.3 基于射线追踪的采样模型射线追踪模拟雷达发射电磁波,跟踪电磁波与目标之间的相互作用过程。由射线追踪建立目标与二维SAR图像之间的映射关系。在仿真中,射线追踪部分借助Pov-Ray光学渲染软件实现。不同于光学成像原理,在SAR成像中,雷达发射与接收电磁波位于同一位置,且成像方式为斜距成像,因此要根据成像原理修改成像程序。具体流程如下:
1) 在同一坐标系下导入目标的三维模型及表面特征、雷达的位置及近距入射角。
2) 根据成像场景及仿真参数确定射线的数量。场景距离向幅宽为X,方位向为Y,分辨率为Δx、Δy,则射线数目为nx=N·X/Δx, N=1, 2, 3,…,N的取值表示采样时每个分辨单元内散射点数目,N取整数使得仿真图像更加平滑逼真。方位向同理。
3) 在雷达与场景间进行射线追踪。以雷达的位置S为原点,雷达电磁波的入射方向为射线方向生成射线族,对每条射线的追踪结果用一个数组Pn=[xnznrnInbnfnXnYnZn]记录。yn、zn和rn表示采样点的回波相位中心方位向、高度向及斜距距离坐标,In是雷达接收到的信号强度,由散射模型计算,bn记录反射次数,fn标记是否发生镜面散射,Xn, Yn, Zn为射线与场景目标第一次相交的交点坐标。以射线在目标表面发生二次散射为例,如图 1所示,射线在场景中的交点为P1(x1, y1, z1)和P2(x2, y2, z2),根据斜距成像的原理,射线的回波相位中心距离向坐标rn为射线路径r1、r12及r2路径之和的一半,更多次散射计算同理。方位向xn及高度向zn的计算也采取各交点坐标平均的方式,即
| $ \left\{ \begin{array}{l} {y_n} = \frac{{{y_1} + {y_2}}}{2}, \\ {z_n} = \frac{{{z_1} + {z_2}}}{2}, \\ {r_n} = \frac{{\left| {{\mathit{\boldsymbol{r}}_1}} \right| + \left| {{\mathit{\boldsymbol{r}}_{12}}} \right| + \left| {{\mathit{\boldsymbol{r}}_2}} \right|}}{2}. \end{array} \right. $ | (4) |
每发生一次镜面反射,fn置1,bn值加1。当射线不再与场景有交点或反射次数达到最大设定值、回波能量达到最小阈值,对本射线的追踪停止。
1.4 后处理模型在采样的过程中,认为电磁波的能量照射到一个分辨单元内,信号被聚焦为一个像素点,相邻的分辨单元内没有相互影响,在这种假设下得到的是带宽无限的理想反射强度图。此时,需要引入点扩散函数与强度图进行卷积,点扩散函数选用Hamming窗函数:
| $ \begin{array}{l} W\left( {n, \alpha } \right){\rm{ = }}\alpha {\rm{ + }}\left( {1{\rm{ - }}\alpha } \right)\cos \left( {\frac{{2\pi n}}{{N - 1}}} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le n \le N - 1. \end{array} $ | (5) |
式中:N表示信号长度;α的值决定窗的陡峭程度,工程实践中一般取α=0.54。将散射强度图进行傅里叶变换,在频域对二维的散射强度图和Hamming窗函数进行卷积,最后再将所得结果进行傅里叶逆变换,得到空域的散射强度图。
另外,采样过程选取的是像素点的散射模型,在将采样点的坐标按斜距成像映射到成像平面时,会出现多个采样点映射到单个分辨单元,也会出现有些分辨单元没有映射的情况。这便导致一次散射图像中易出现明暗相间的条纹特征。增加采样率可以减缓条纹,但采样率增加使得运算量大幅增加。故本文采用在一次反射矩阵中插值的方法来解决。插值选用三次样条插值,保证数据有良好的稳定性和收敛性,减少仿真误差的引入。
仿真过程采用的是非相干方式的SAR仿真方法,得到的散射强度图没有噪声,然而斑点噪声是SAR图像的一个显著特征,需要对图像添加噪声以接近仿真图像。相干斑在统计意义上可以用乘性噪声模型进行描述,本文采用瑞利相干斑模型为图像添加乘性噪声。瑞利噪声的二维分布密度函数为
| $ {p_R}\left( {x, y} \right) = \left\{ \begin{array}{l} \frac{x}{{\mu _1^2}}{{\rm{e}}^{\frac{{ - {x^2}}}{{2\mu _1^2}}}} \cdot \frac{y}{{\mu _2^2}}{{\rm{e}}^{\frac{{ - {y^2}}}{{2\mu _2^2}}}}, \;\;\;\;\;x \ge 0, \\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x < 0. \end{array} \right. $ | (6) |
式中:μ1、μ2分别为图像在距离向和方位向的强度均值。
对于强度图中的每一个分辨单元,首先产生一个服从瑞利分布的均值为1的随机数,得到噪声的强度值。然后将分辨单元的强度值与噪声的值相乘,即可得到本分辨单元带有斑点噪声的散射强度值,最终得到含有斑点噪声的仿真SAR图像,计算公式为
| $ \Delta \hat y\left( {x, y} \right) = \gamma \left( {x, y} \right) * n\left( {x, y} \right). $ | (7) |
式中:γ(x, y)表示散射强度图中(x, y)处的散射强度值;n(x, y)是对应的噪声强度;
基于图像几何特征的高分辨率SAR图像仿真流程如图 2所示。

|
Download:
|
| 图 2 高分辨率SAR图像仿真流程图 Fig. 2 Flowchart of VHR SAR image simulation | |
1) 首先,建立仿真目标的三维模型,借助图形学的建模软件如Auto CAD、3DS Max等制作完成。然后根据雷达工作参数建立局部O-XYZ直角坐标系,明确雷达的飞行高度、飞行方向、姿态角、分辨率、目标的三维坐标,以及方位向距离向与X轴、Y轴的对应关系。至此,成像几何模型建立。
2) 其次,在雷达与目标场景间展开射线追踪,仿真电磁波的反射过程。射线追踪结束,输出一个多行的矩阵,矩阵的每一行代表一个采样点的信息,包含采样点的位置、强度、散射类型、散射次数等。根据散射次数的不同,将采样点信息矩阵分层存储为一次散射矩阵、二次散射矩阵等。
3) 然后,根据雷达成像原理,生成散射强度图。散射强度图的高度NH和宽度NW的计算公式为
| $ \left\{ \begin{array}{l} {N_{\rm{H}}} = \frac{X}{{\Delta x}} + 1, \\ {N_{\rm{W}}} = \frac{Y}{{\Delta y}} + 1, \end{array} \right. $ | (8) |
| $ \left\{ \begin{array}{l} {N_{{\rm{W}}n}} = \frac{{{N_{\rm{W}}}}}{{{r_{\max }} - {r_{\min }}}} \cdot \left( {{r_n} - {r_{\min }}} \right), \\ {N_{{\rm{H}}n}} = {y_n}. \end{array} \right. $ | (9) |
根据斜距rn和方位yn求得散射点在散射强度图中的位置,由于雷达工作在正侧视条件下,故方位向坐标NHn=yn。将散射强度In映射到空白图像中对应的分辨单元,当有多个回波能量映射到同一个分辨单元时,对这些能量进行非相干叠加。最后对整幅图像进行灰度归一化处理,得到各层的散射强度图。也可以根据发生镜面反射与否作为标志,生成镜面散射图与非镜面散射图。
4) 最后,对散射强度图进行后处理。根据后处理模型,对一次散射矩阵进行三次样条插值,再将各散射层级的图像叠加,得到全层级的散射图像;接着在频域对点扩散函数与散射图进行卷积,傅里叶逆变换得到时域图像,在图像中添加乘性噪声。最终,得到高分辨率的SAR仿真图像。
3 仿真结果及分析为验证本文所提方法的有效性,选取4组具有代表性的目标进行实验。前3组实验中,雷达的工作参数如表 1所示。
|
|
表 1 高分辨率SAR仿真参数 Table 1 VHR SAR simulation parameters |
第1组实验以三面角反射器为目标,仿真模型及结果如图 3所示。角反射器对入射电磁波有汇聚作用,在建筑物目标中,窗台、窗框及与地面垂直的墙壁等结构极易构成三面角反射器。本文选取边长20 cm的角反射器作为测试目标。图 3(b)、3(c)分别是单个角反射器的仿真SAR图像与实测SAR图像。从仿真图像同实际SAR图像的对比可得,三面角反射器在SAR图像中以点目标的形式呈现,表现为一个边缘扩散的高亮度分辨单元,从像素级别验证了本文所提方法的有效性。

|
Download:
|
| 图 3 角反射器的仿真实验 Fig. 3 Experiments for corner reflector | |
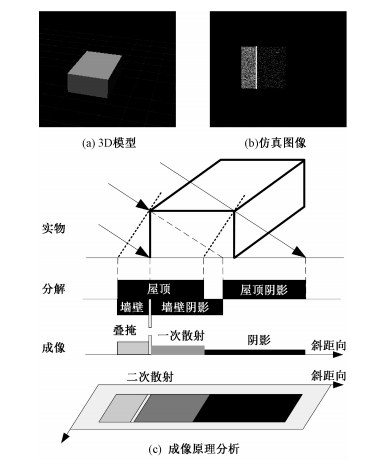
第2组实验选取简易的平顶房屋作为三维模型,并将仿真SAR图像与理论分析图像对比。图 4(a)表示一个长宽高为30 m×20 m×10 m的平顶屋,雷达飞行方向与屋顶的长边方向一致,仿真结果如图 4(b)所示,一次散射由屋顶和墙壁区域形成,由于斜距成像的原因,墙壁和屋顶产生叠掩。墙壁与地面垂直形成二面角,仿真图像上电磁波的相位中心位于墙角位置,回波叠加后出现二次散射亮线。电磁波照射不到的地方形成阴影区。对比图 4(c)可得,叠掩、阴影、顶底倒置及二次散射的亮线等几何特征均与理论分析结果一致,证明了本方法能较好的模拟简单建筑的几何特征。
|
Download:
|
| 图 4 平顶房屋的仿真及分析图 Fig. 4 Simulation and analysis images of flat-roof building | |
第3组实验选取带窗户的房屋和有栏杆的筒仓模型进行实验。图 5(a)表示10 m×10 m×5 m的带窗房屋,包含窗户、窗框等元素,方位角为45°。图 5(b)表示筒仓的三维模型,外墙曲面以三角平面近似。图 6表示带窗户房屋的全散射和各次散射图。一次散射形成图像轮廓,二次散射发生在墙角和窗框部分,三次及以上的散射只发生在窗户部分。在多次散射中,斜距等于电磁波传播总路程的一半,故窗框四次、五次散射的位置其比一次散射的位置靠右。墙面每侧的3个亮区由3个窗户散射形成。

|
Download:
|
| 图 5 仿真目标的三维模型 Fig. 5 3D model of simulation targets | |

|
Download:
|
| 图 6 带窗房屋的仿真图像 Fig. 6 Simulation images of the building with windows | |
对筒仓模型的仿真结果如图 7所示,图 7(a)其中图 7(b)为散射层级分布图。无论是平面建筑还是曲面建筑,仿真结果都体现了叠掩、阴影、多次散射等几何特征。对于窗户、栏杆等建筑细节的仿真,说明本方法在高分辨率仿真中具有可行性。

|
Download:
|
| 图 7 筒仓的仿真图像和散射分布图 Fig. 7 Simulation and distribution images of silo | |
第4组实验选取多伦多地区某组合建筑物为目标,其光学航拍图像及三维模型如图 8所示。在实验中,雷达的中心频率为9.65 GHz,带宽为0.15 GHz,俯仰角为46°,采样间隔为1.1 m,组合建筑的三维模型由Google Earth数据获取,雷达入射角与建筑物侧边的夹角为30°。

|
Download:
|
| 图 8 组合建筑物的航拍图及三维模型 Fig. 8 Aerial photo and 3D model of combination building | |
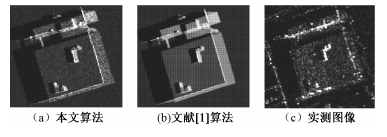
采用本文算法进行仿真,得到仿真图像如图 9(a)所示,由文献[1]算法得到仿真结果如图 9(b)所示,将仿真结果分别与实测图像图 9(c)进行对比。
|
Download:
|
| 图 9 组合建筑物的实测SAR图像及仿真SAR图像 Fig. 9 Real and simulation SAR images of combination building | |
仿真图像中建筑物的几何特征均能与实测SAR图像保持一致。由于文献[1]中对分辨单元内散射点的处理不充分,没有充分考虑散射模型、噪声及带宽等因素,仿真图像中出现了明暗相间的条纹特征,对比实测SAR图像可得,本文的仿真结果更加逼真。但真实SAR图像中有部分亮点在本文算法的仿真SAR图像中没有对应,是因为对建筑物的建模精度不够,阁楼、窗户、金属空调架以及屋顶的通风口等建筑构件在建模中被忽略了。因此,提高建模精度是得到逼真SAR图像的关键因素。
综合以上实验结果可得,针对规则的建筑物目标,本文的仿真方法可以得到几何特征一致的逼真SAR图像。
4 结论本文提出一种基于建筑物几何特征的高分辨率SAR图像仿真方法,该方法首先根据三维场景模型和雷达的工作参数构建成像几何模型,然后基于改进的Phong Shading散射模型,在场景间展开射线追踪,得到采样点的散射信息矩阵,接着将得到的采样点数据进行后处理,最终得到高分辨率的仿真SAR图像。分析和仿真结果表明,该方法能够准确、高效的仿真建筑物在SAR图像中的几何特征,后处理过程严格考虑了SAR实际成像过程中的带宽、噪声等影响因素,另外,分层的数据处理方法为后续研究散射特征提供了基础。下一步将研究仿真图像在图像建筑物提取及目标重建中的作用。
| [1] |
Auer S, Hinz S, Bamler R. Ray-tracing simulation techniques for understanding high resolution SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1445-1456. DOI:10.1109/TGRS.2009.2029339 |
| [2] |
Balz T, Hammer H, Auer S. Potential and limitations of SAR image simulators:a comparative study of three simulation approaches[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 101: 102-109. DOI:10.1016/j.isprsjprs.2014.12.008 |
| [3] |
董纯柱, 胡利平, 朱国庆, 等. 地面车辆目标高质量SAR图像快速仿真方法[J]. 雷达学报, 2015, 4(3): 351-360. |
| [4] |
Franceschetti G, Iodice A, Riccio D, et al. SAR raw signal simulation for urban structures[J]. IEEE Transactions on Geoscience and Remote Sensing Letters, 2003, 41(9): 1986-1995. DOI:10.1109/TGRS.2003.814626 |
| [5] |
Franceschetti G, Iodice A, Riccio D. A canonical problem in electromagnetic backscattering from buildings[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1787-1801. DOI:10.1109/TGRS.2002.802459 |
| [6] |
Franceschetti G, Guida R, Lodice A, et al. Simulation tools for interpretation of high resolution SAR images of urban areas[C]//IEEE Urban Remote Sensing Joint Event, Paris, France, 2007, 18: 1-5. http://www.researchgate.net/publication/4254406_Simulation_Tools_for_Interpretation_of_High_Resolution_SAR_Images_of_Urban_Areas
|
| [7] |
Chen H Z, Zhang Y T, Wang H Q, et al. SAR imaging simulation for urban structure based on analytical models[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(6): 1127-1131. DOI:10.1109/LGRS.2012.2190969 |
| [8] |
Kulpa K S, Samczynski P, Malanowski M, et al. An advanced SAR simulator of three-dimensional structures combing geometrical optics and full-wave electromagnetic method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 776-784. DOI:10.1109/TGRS.2013.2283267 |
| [9] |
Xu F, Jin Y Q. Imaging simulation of polarimetric SAR for a comprehensive terrain scene using the mapping and projection algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(11): 3219-3234. DOI:10.1109/TGRS.2006.879544 |
| [10] |
Delliere J, Maitre H, Maruani A. SAR measurement simulation on urban structures using a FDTD technique[C]//IEEE Urban Remote Sensing Joint Event, Shanghai, China, 2007: 1-8. https://www.researchgate.net/publication/4254401_SAR_measurement_simulation_on_urban_structures_using_a_FDTD_technique
|
| [11] |
Stefan A. 3D synthetic aperture radar simulation for interpreting complex urban reflection scenarios[D]. Munich: Technical University of Munich, 2011. https://www.researchgate.net/publication/50904214_3D_Synthetic_Aperture_Radar_Simulation_for_Interpreting_Complex_Urban_Reflection_Scenarios
|
| [12] |
Balz T, Stilla U. Hybrid GPU-Based Single- and Double-Bounce SAR Simulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(10): 3519-3529. DOI:10.1109/TGRS.2009.2022326 |
| [13] |
Bolter R. Reconstruction of man-made objects from high resolution SAR images[C]//IEEE Aerospace Conference Proceedings, Big Sky, USA, 2000, 3: 287-292. http://www.researchgate.net/publication/3869131_Reconstruction_of_man-made_objects_from_high_resolution_SAR_images
|
| [14] |
Hammer H, Karsten S. Coherent simulation of SAR images[J]. Proc. SPIE 7477, Image Signal Processing for Remote Sensing, 2009, 7477: 74771G-9. |
| [15] |
Auer S, Gernhardt S, Bamler R. Ghost persistent scatters related to multiple signal reflections[J]. IEEE Transactions on Geoscience and Remote Sensing Letters, 2011, 8(5): 919-923. DOI:10.1109/LGRS.2011.2134066 |
| [16] |
王国军.建筑物目标高分辨率SAR图像理解研究[D].北京: 中国科学院大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2609775
|
| [17] |
Raffaella G, Antonio I, Daniele R. Model-Based Interpretation of High-Resolution SAR Images of Buildings[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2008, 1(2): 107-119. DOI:10.1109/JSTARS.2008.2001155 |
| [18] |
熊文昌.人造目标SAR图像仿真及其在解译中的应用[D].北京: 中国科学院大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2613932
|
 2018, Vol. 35
2018, Vol. 35 


