2. 中国农业科学院农业资源与农业区划研究所, 北京 100081
2. Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Beijing 100081, China
土壤含水量是描述地表与大气之间水分和能量交换的重要参量,精确估算土壤含水量在时空尺度上的变化,对气候变化、农业生产、环境监测等领域的研究具有重要意义[1-6]。目前,虽然被动微波数据在土壤含水量反演和产品生产方面呈现出较大的潜力,但是由于受地表粗糙度、植被覆盖度等微波后向散射系数等因素的影响,使得建立通用的微波土壤含水量反演算法较为困难[7-10]。相较而言,可见光/近红外与热红外遥感反演土壤含水量的方法相对成熟,且简单易行,是目前最常用的遥感反演土壤含水量的方法之一[11-13]。可见光/近红外与热红外遥感土壤含水量反演方法包括植被指数法、热惯量法和地表温度-植被指数特征空间法[14-17]。其中,地表温度-植被指数特征空间法是最常用的方法。
研究表明地表温度与植被指数可以提供植被水分胁迫条件和土壤湿度信息[18]。如果研究区域中包含足够的像元,且云和水体的影响均被去除,地表温度和植被指数构成的二维散点图呈三角形或梯形形状[19]。根据地表温度和植被指数构成的特征空间,Price[20]首先提出三角形特征空间的概念。他利用遥感AVHRR (advanced very high resolution radiometer)数据构建地表温度-植被指数特征空间,并且分析特征空间与土壤含水量的关系。Nemani等[21]研究地形和植被类型对地表温度-植被指数特征空间的影响,提出自动确定干湿边的方法。三角形特征空间方法如图 1所示,地表温度-植被指数特征空间受干边和湿边的限制。特征空间中的湿边表征最大蒸散发和土壤含水量充足的状态,干边表征蒸散发达到最小值,植被的生长受到水分胁迫,土壤含水量为0的状态。但是,在瞬时地表温度与植被指数构成的特征空间中,地表温度的精度直接影响土壤含水量的估算结果,且前的方法多数是基于极轨卫星数据发展而来,可能出现瞬时数据缺失的情况。

|
Download:
|
| 图 1 地表温度-植被指数特征空间示意图 Fig. 1 LST-Ⅵ space | |
地表温度日较差是一天中最高温和最低温的差值[22],是表征气候变化的重要指示因子,对云覆盖、降雨、地表径流等因素较为敏感[23]。通过Zhang等[24]和Leng等[25]利用温度的时间变化信息构建特征空间的研究表明,温度的日变化信息能够用于土壤含水量反演。且利用温度的日变化而不是瞬时温度来反演土壤含水量,能够减小温度反演误差给土壤含水量反演结果带来的不确定性。本文使用Duan等[26]的方法直接从星上亮温数据计算地表温度日较差,不需要地表温度的反演过程,避免了计算地表温度时产生的误差。
基于此,本文利用静止气象卫星高时间分辨率的特点,以伊比利亚半岛为研究区域,利用地表温度日较差DTR (diurnal temperature range)和植被覆盖度FVC (fractional vegetation cover)代替地表温度LST (land surface temperature)和植被覆盖度FVC,构建DTR-FVC特征空间,减小由瞬时地表温度的不确定性带来的土壤含水量估算误差,提高土壤含水量的反演精度。
1 研究区域和数据 1.1 研究区域考虑到位于西欧的伊比利亚半岛地区晴空无云的天气较多,用于研究的MSG-SEVIRI数据主要覆盖欧洲和非洲地区,能够提供有效的卫星数据,且该地区有土壤含水量地面观测数据,该观测数据被广泛用来验证不同土壤含水量产品,因此本文选择伊比利亚半岛作为研究区(12°W~4°E,33°N~45°N),图 2为研究区域的高程图。该地区气候温和,海洋性特征显著,夏季炎热干燥,冬季温和多雨。土地覆盖类型以农田、稀疏的植被以及开阔的灌木丛为主。

|
Download:
|
| 图 2 研究区域的地表高程图 Fig. 2 Elevation in the study area | |
本文使用2012年的MSG-SEVIRI遥感数据进行土壤含水量的反演研究。
SEVIRI传感器是搭载在MSG卫星上的新型传感器,包括一个红外通道、一个近红外通道和两个热红外通道。该传感器具有较高的时间分辨率,每15 min获取一次地面数据,一天可以获得96个时刻的数据。该传感器的星下分辨率较低,为3 km,高分辨率通道星下点的空间分辨率可以达到1 km。
文中使用的MSG-SEVIRI遥感数据分为4种:1) MSG Level-1.5影像数据;2)云掩膜数据;3)植被覆盖度数据;4)地表温度数据。其中,MSG Level-1.5数据和云掩膜数据来源于EUMETSAT (Europe Organisation for the Exploitation of Meteorological Satellites)网站(http://eoportal.eumetsat.int./),植被覆盖度数据和地表温度数据从LSA SAF (Land Surface Analysis Satellite Applications Facility)下载得到(https://landsaf.ipma.pt)。
MSG Level-1.5影像数据是以二进制格式存储的未经辐射校正的影像数据,文中使用SPT (SEVIRI Pre-processing Toolbox)软件将该数据转换为MSG-SEVIRI第9 (10.8 μm)、第10 (12.0 μm)通道的TOA (Top-of-the-Atmosphere)亮温数据。
云掩膜数据中的像元可以分为以下4类:1)有云;2)陆表晴空;3)海表晴空;4)未处理。本文中需要使用陆表晴空数据,所以要用云掩膜数据剔除亮温数据中受云影响的像元。
1.2.2 土壤质地数据研究区的土壤质地数据由联合国粮农组织(FAO)和维也纳国际应用系统研究所(IIASA)所建立的世界土壤数据库HWSD (Harmonized World Soil Database)下载得到(http://www.fao.org/soils-portal/en),该数据包括一幅全球栅格影像及对应的属性数据库。属性数据库中包含每个像元对应的土壤参数,包括有机碳含量、pH值、土壤蓄水能力、0~10 cm深度的土壤含沙量和黏土含量等,数据空间分辨率为1 km。文中需要使用土壤含沙量和黏土含量计算土壤饱和含水量及萎蔫系数,土壤质地数据在使用前需要与遥感数据进行空间匹配。
1.2.3 土壤含水量测量数据用于验证的土壤含水量地面实测数据来自西班牙Duero盆地中部地区的REMEDHUS土壤含水量观测网络(41.1°N~41.5°N,5.1°W~5.7°W)。REMEDHUS土壤含水量观测网络占地约1 300 km2,地形较为平坦,高程约700~900 m。文中使用的REMEDHUS 2012年土壤含水量实测数据来源于国际土壤含水量观测网络(http://ismm/geo.tuwien.ac.cn),在此期间共有19个站点提供可利用的土壤含水量数据,观测步长为1 h。
表 1给出每个站点的名称、土壤质地以及经纬度数据。
|
|
表 1 REMEDHUS土壤含水量观测网络站点信息 Table 1 Information of the REMEDHUS soil moisture observation network |
本文主要基于温度日较差-植被覆盖度特征空间建立土壤含水量反演模型反演土壤含水量,利用实测数据对土壤含水量的反演结果进行分析和验证,并与地表温度-植被覆盖度特征空间的土壤含水量反演结果进行对比分析,图 3描述本文主要的技术流程。

|
Download:
|
| 图 3 土壤含水量反演方法流程图 Fig. 3 Flow chart of the soil moisture retrieval method | |
温度日较差DTR是表征气候变化的重要指示因子,也是利用遥感数据反演热惯量的关键参数[27]。地表温度日较差定义为一天中最高的地表温度(Tmax)和最低的地表温度(Tmin)之间的差值:
| $ \text{DTR=}{{T}_{\max }}-{{T}_{\min }}, $ | (1) |
式中:Tmax为一天中的最高温度(K),Tmin为一天中的最低温度(K)。
根据Duan等[26]改进的温度日变化模型,时间t和参考时间tr之间的温差ΔTs日变化可以由公式(2),即温差日变化DTDC (diurnal temperature difference cycle)模型来表示
| $ \begin{align} & \Delta T_{\text{s}}^{d}\left( t \right)={{T}_{\text{a}}}\cos \left( \frac{\pi }{\omega }\left( t-{{t}_{\text{m}}} \right) \right)- \\ & \ \ \ {{T}_{\text{a}}}\cos \left( \frac{\pi }{\omega }\left( t-{{t}_{\text{m}}} \right) \right), t < {{t}_{\text{s}}}, \\ & \Delta T_{\text{s}}^{n}\left( t \right)=\delta T\text{+}\left[ {{T}_{\text{a}}}\cos \left( \frac{\pi }{\omega }\left( {t_{\text{s}}}-{{t}_{\text{m}}} \right) \right)\text{-}\delta T \right] \\ & \frac{k}{\left( k+t-{{t}_{\text{s}}} \right)}-{{T}_{\text{a}}}\cos \left( \frac{\pi }{\omega }\left( {t_{\text{r}}}-{{t}_{\text{m}}} \right) \right), t\ge {{t}_{\text{s}}}. \\ \end{align} $ | (2) |
式中:Ta为温度振幅(K),tm为温度达到最大值的时间,ts表示自由衰减开始的时间,δT为日出时的剩余温度T0与T(t→∞)之间的温差(K)。
当t=tm时,由公式(2)可得
| $ \Delta {{T}_{\max }}={{T}_{\text{a}}}-{{T}_{\text{a}}}\cos \left( \frac{\pi }{\omega }\left( {{t}_{\text{r}}}-{{t}_{\text{m}}} \right) \right). $ | (3) |
当t→∞时,由公式(2)可得
| $ \Delta {{T}_{\min }}=\delta T-{{T}_{\text{a}}}\cos \left( \frac{\pi }{\omega }\left( {{t}_{\text{r}}}-{{t}_{\text{m}}} \right) \right). $ | (4) |
公式(3)减去公式(4),则可以得到地表温度日较差,即
| $ \text{DTR=}\Delta {{T}_{\max }}-\Delta {{T}_{\min }}\approx {{T}_{\text{a}}}-\delta T. $ | (5) |
通过分裂窗算法,一天中时间t和参考时间tr之间的温差日变化[26]可以由MSG-SEVIRI第9、第10通道的TOA亮温计算得到:
| $ \begin{align} & \Delta {{T}_{\text{s}}}\left( t \right)={{T}_{\text{s}}}\left( t \right)\text{-}{{T}_{\text{s}}}\left( {{t}_{\text{r}}} \right) \\ & \ \ \ \ \ \ \ \ \ \ ={{T}_{9}}\left( t \right)+a\left[ {{T}_{9}}\left( t \right)-{{T}_{10}}\left( t \right) \right]+ \\ & b{{\left[ {{T}_{9}}\left( t \right)-{{T}_{10}}\left( t \right) \right]}^{2}}- \\ & \left\{ {{T}_{9}}\left( {{t}_{\text{r}}} \right)+a\left[ {{T}_{9}}\left( {{t}_{\text{r}}} \right)-{{T}_{10}}\left( {{t}_{\text{r}}} \right) \right]+ \right. \\ & \left. b{{\left[ {{T}_{9}}\left( {{t}_{\text{r}}} \right)-{{T}_{10}}\left( {{t}_{\text{r}}} \right) \right]}^{2}} \right\}. \\ \end{align} $ | (6) |
式中:T9和T10分别为MSG-SEVIRI第9、第10通道的TOA亮温;a、b为回归系数。
式(2)等号左边的部分可以由式(6)计算得出。在无需已知地表温度和发射率的情况下,利用DTDC模型(式(2))拟合地表温差日变化曲线(式(6)),可以直接得到DTDC模型的4个参数Ta,tm,δT,ts。在计算过程中,Duan等[26]将tr设置为每个像元的当地太阳时13:00。DTDC模型中自由参数的初始值设置为Ta=ΔTmax-ΔTmin,δT=0.5 K,tm=12.5 h,ts=17 h。由于自由参数的初始值与最终值相近,DTDC模型的结果通常会迅速收敛到最终值。图 4为利用DTDC模型拟合地表温差日变化曲线。使用Duan等[26]提出的计算温度日较差的方法,可以在无需得到地表温度和地表发射率的情况下,利用静止气象卫星的星上亮温数据直接计算得到温度日较差,避免计算地表温度时造成的误差。

|
Download:
|
| 图 4 DTDC模型拟合地表温差日变化曲线 Fig. 4 Fitting the DTDC model to the diurnal ΔT cycle | |
利用MSG Level-1.5影像数据和云掩膜数据计算出当天的温度日较差,温度日较差与植被覆盖度构成的二维散点图如图 5所示。从图 5可以看出,温度日较差与植被覆盖度构成的二维散点图呈三角形,当植被覆盖度增加时,温度日较差降低。

|
Download:
|
| 图 5 温度日较差-植被覆盖度二维散点图 Fig. 5 DTR-FVC scatter plot and the observed limiting edges | |
与LST-FVC特征空间类似,在DTR-FVC特征空间中,干边表征没有蒸散发和可利用水分的情况,湿边表示水分充足且植被不受土壤含水量胁迫的情况[28]。三角形算法的一个主要限制是特征空间干湿边的确定,干湿边通常使用经验拟合或物理方程确定[29]。通过干湿点像元拟合直接提取干湿边的方法简单易行,操作性强,不需要辅助数据,但容易受到异常值和大气状况的影响,导致一定的误差。通过地表能量平衡方程求解干湿边的方法精度较高,但需要辅助数据,计算复杂[30]。
本文使用干湿点像元拟合直接提取干湿边的方法,方法的主要思路是将植被覆盖度分为等间隔的20个区间,并将每个区间等分为5个等间隔的子区间。为减少异常值带来的误差,将每个区间内拥有最大温度日较差的子区间剔除,然后对剩余的4个子区间的最大温度日较差取平均值作为该区间的最大温度日较差,最后将20个区间的最大温度日较差与植被覆盖度进行线性拟合得到观测干边。湿边的求解方法类似于干边。
本文使用上述提取观测干湿边的方法,得到的拟合观测干边如图 5中的红线所示,湿边如图 5中的绿线所示。在DTR-FVC特征空间中,对于给定的植被覆盖度FVCi,DTR从最小值(DTRi, min)到最大值(DTRi, max)变化,对应的土壤含水量从最高(SMi, max)到最低(SMi, min)变化。DTRi, max由DTRi, max=a1·FVCi+b1得到,DTRi, min由DTRi, min=a2·FVCi+b2得到。其中,a1,a2,b1,b2均为拟合系数。从图中可以看出,利用散点拟合得到的观测湿边存在很多异常点,这些点主要受到云的影响的像元。
Sandholt等[29]提出,在给定的植被覆盖和环境条件下,地表温度会随着土壤含水量的增加而降低。他们认为地表温度/归一化植被指数特征空间中存在一系列的土壤含水量等值线,这些等值线是不同土壤含水量条件下地表温度与归一化植被指数的斜率。
由于遥感获取瞬时地表温度带来一定的误差,所以很多学者研究利用地表温差来估算土壤含水量,如Zhang等[24]提出的温度变化率植被干旱模型(TRRVDI)。
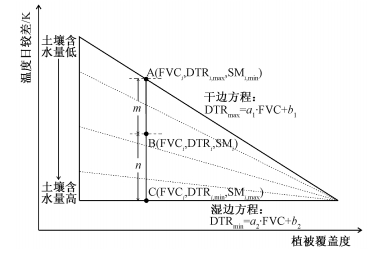
当植被覆盖度一定时,温度日较差与土壤含水量密切相关。利用这一关系,构建温度日较差-植被覆盖度三角形特征空间,如图 6所示。y轴表示一天的温度日较差(K),x轴表示植被覆盖度。观测干边表示土壤含水量达到最小值,观测湿边表示土壤含水量充足的情况。其中,假设条件为温度日较差与植被覆盖度呈线性关系,且土壤含水量从干边到湿边线性变化。特征空间内的插值表示土壤含水量、温度日较差以及植被覆盖度三者之间的关系,基于DTR-FVC特征空间,对于特定的像元B (FVCi, DTRi, SMi),则有
| $ \frac{\text{DT}{{\text{R}}_{i}}-\text{DT}{{\text{R}}_{i, \min }}}{\text{DT}{{\text{R}}_{i, \max }}-\text{DT}{{\text{R}}_{i, \min }}}=\frac{n}{m+n}=\frac{{{{\rm SM}}_{i}}-{{{\rm SM}}_{i, \max }}}{{{{\rm SM}}_{i, min}}-{{{\rm SM}}_{i, \max }}} $ | (7) |
|
Download:
|
| 图 6 温度日较差-植被覆盖度特征空间 Fig. 6 DTR-FVC space | |
式中:DTRi为像元i的温度日较差(K);SMi为像元i的实际土壤含水量(m3/m3);SMi, min为像元i的最小土壤含水量(m3/m3); SMi, max为像元i的最大土壤含水量。对式(7)等号两边进行变形可得
| $ \begin{align} & {{{\rm SM}}_{i}}={{{\rm SM}}_{i, \max }}- \\ & \ \ \ \ \ \ \ \ \ \frac{\text{DT}{{\text{R}}_{i}}-\text{DT}{{\text{R}}_{i, \min }}}{\text{DT}{{\text{R}}_{i, \max}}-\text{DT}{{\text{R}}_{i, \min }}}\cdot \left( {{{\rm SM}}_{i, \max }}-{{{\rm SM}}_{i, \min }} \right). \\ \end{align} $ | (8) |
在大多数情况下,一个区域内土壤含水量不会处于极高或极低的状态。最大土壤含水量一般处于田间持水量与饱和含水量之间,最小土壤含水量一般在萎蔫系数和剩余土壤含水量之间[31]。但是田间持水量、饱和含水量、萎蔫系数以及剩余土壤含水量这4个参数都属于水文参数,通常需要在实验室条件下进行测定。
本文假设最大土壤含水量等于饱和含水量,最小土壤含水量等于萎蔫系数。根据式(8),土壤含水量可表示为
| $ {{{\rm SM}}_{i}}=\text{SAT}-\frac{\text{DT}{{\text{R}}_{i}}-\text{DT}{{\text{R}}_{i, \min }}}{\text{DT}{{\text{R}}_{i, \max}}-\text{DT}{{\text{R}}_{i, \min }}}\cdot \left( \text{SAT-WP} \right), $ | (9) |
式中:SAT为饱和含水量(m3/m3);WP为萎蔫系数(m3/m3)。Saxton和Rawls[32]提出利用土壤含沙量和黏土含量两个土壤质地参数计算土壤饱和含水量和萎蔫系数的算法,研究区的土壤含沙量及黏土含量来源于土壤质地数据。
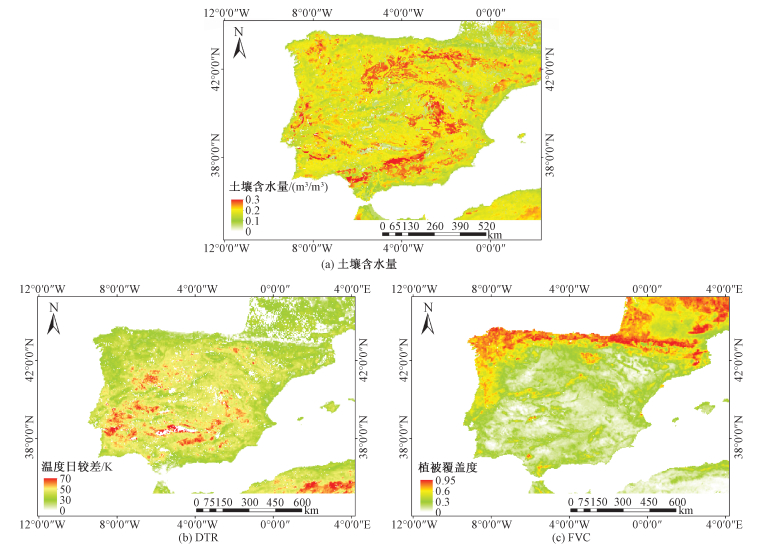
3 结果与分析图 7(a)~7(c)分别显示2012年7月16日研究区由DTR-FVC特征空间估算的土壤含水量、温度日较差以及植被覆盖度的空间分布图。可以看出,研究区内的植被覆盖度大部分在0.5左右,且北部地区的植被覆盖度明显高于南部。温度日较差在0~70 K之间变化,且内陆地区的温度日较差高于沿海地区。土壤含水量在0~0.3 m3/m3之间变化,东部地区的土壤含水量高于西部。
|
Download:
|
| 图 7 研究区的土壤含水量、温度日较差和植被覆盖度的分布情况 Fig. 7 Distributions of soil moisture (a), DTR(b), and FVC (c) in the study area | |
图 8(a)~8(d)分别为1月2日、4月12日、6月7日和7月22日利用DTR-FVC特征空间估算的土壤含水量与实测土壤含水量之间的对比图。从图 8可以看出,这4天估算土壤含水量与实测土壤含水量之间的RMSE均在0.05 m3/m3以内,Bias均小于0.025 m3/m3,反演精度较高,说明利用该算法可以较好地反演土壤含水量。

|
Download:
|
| 图 8 利用DTR-FVC特征空间估算土壤含水量与实测土壤含水量的对比图 Fig. 8 Comparison between the estimated soil moisture using the DTR-FVC space and the observed soil moisture | |
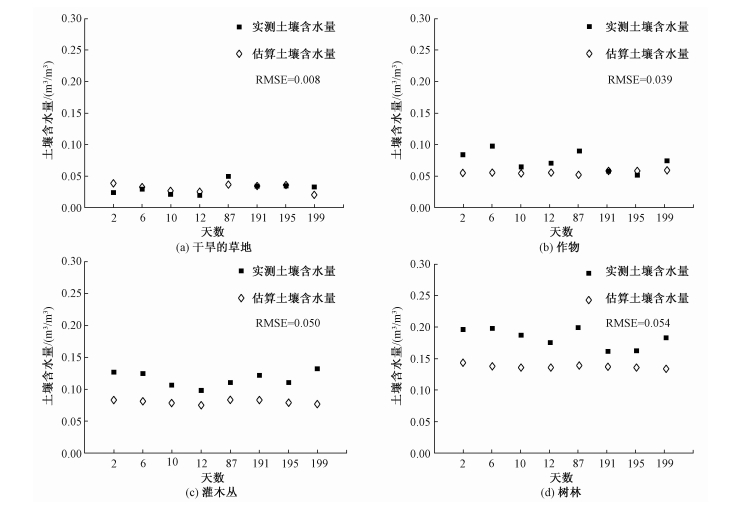
图 9是不同土地覆盖类型下利用DTR-FVC特征空间估算的土壤含水量与实测土壤含水量之间的对比图:9(a)干旱的草地;9(b)作物;9(c)灌木丛;9(d)树林。这4幅图都是利用2012年第2天到第200天中共8天的有效数据得到。从图中可以看出,在不同的植被覆盖类型下估算土壤含水量与实测土壤含水量之间的均方根误差都在0.06 m3/m3之内,且土壤含水量较低的干旱草地与作物区域的RMSE小于0.04 m3/m3,在土壤含水量较高的灌木丛和树林区域的RMSE大于0.05 m3/m3。干旱区/半干旱区的估算结果比湿润/半湿润区的估算结果相对要好,说明DTR-FVC特征空间在土壤含水量较低的区域反演精度更高,该方法更适用于干旱、半干旱地区。导致这种结果的原因可能是由于在土壤含水量较低时,观测干湿边更接近于理论值,而使土壤含水量较高时,观测干湿边小于理论值,会使反演结果造成一定的误差。
|
Download:
|
| 图 9 2012年不同土地覆盖类型下估算土壤含水量与实测土壤含水量的对比图 Fig. 9 Estimated soil moisture versus observed soil moisture over different types of land-cover: arid grass(a), cropland (b), shrub (c), and forest (d) in 2012 | |
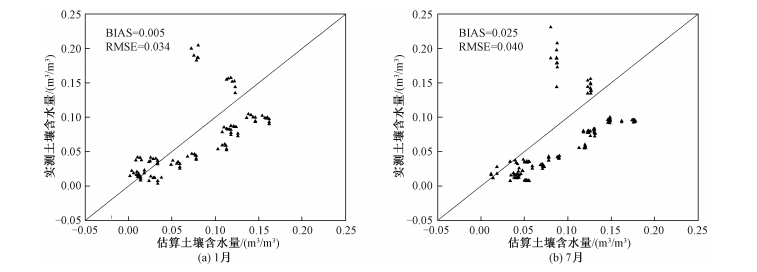
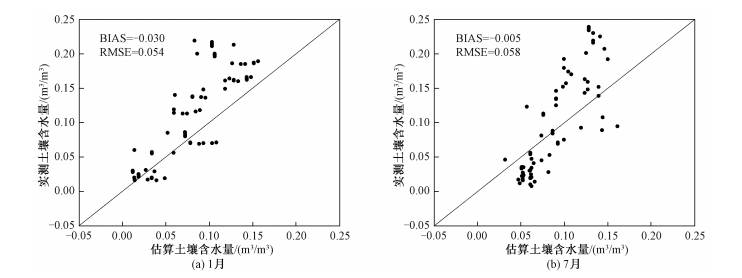
图 10(a)、10(b)分别为1月份和7月份利用DTR-FVC特征空间估算的土壤含水量与实测土壤含水量的对比图,这两个月的均方根误差RMSE分别为0.034和0.040 m3/m3,偏差Bias分别为0.005和0.025 m3/m3。图 11(a)、11(b)分别为1月份和7月份利用LST-FVC特征空间估算的土壤含水量与实测土壤含水量的对比图,这两个月的均方根误差RMSE分别为0.054和0.058 m3/m3,偏差Bias分别为0.030和-0.005 m3/m3。对比图 10和图 11可以发现,使用DTR-FVC特征空间反演土壤含水量的精度比使用LST-FVC特征空间的精度有所提高,均方根误差RMSE减小0.020 m3/m3左右。对比分析结果表明,构建DTR-FVC特征空间,可以减小由瞬时地表温度的不确定性带来的土壤含水量估算误差,提高土壤含水量的反演精度,温度日较差DTR在土壤含水量反演研究中具有一定的潜力。
|
Download:
|
| 图 10 不同月份利用DTR-FVC特征空间方法估算土壤含水量与实测土壤含水量的对比图 Fig. 10 Comparison between estimated soil moisture using the DTR-FVC space and in situ measured soil water content in January (a) and July (b) | |
|
Download:
|
| 图 11 不同月份利用LST-FVC特征空间方法估算土壤含水量与实测土壤含水量的对比图 Fig. 11 Comparison between estimated soil moisture using the LST-FVC space and in situ measured soil water content in January (a) and July (b) | |
总体来说,利用DTR-FVC特征空间计算得到的土壤含水量值高于实测土壤含水量。本文的误差主要来自于以下3点:一是在计算土壤含水量的过程中,无法完全消除云的影响;二是观测干湿边并不能代表真实的土壤含水量的极限条件,观测干边小于实际干边;三是真实的土壤含水量最大值处于田间持水量和饱和含水量之间,水分最小值在萎蔫系数和剩余土壤含水量之间,简单地利用饱和含水量和萎蔫系数表示土壤含水量的最大、最小值会导致一定的误差。
4 结论地表温度-植被指数特征空间法结合可见光与热红外遥感方法反演土壤含水量的优点,可以反映出一定空间尺度上的土壤湿度情况,而且方法简单易用、精度较高,物理意义明确,是一种常用的土壤含水量反演方法。
温度日较差DTR对云覆盖、降雨、地表径流等因素较为敏感,本文提出的DTR-FVC特征空间方法在地表温度-植被指数特征空间原有优势的基础上,减小了由瞬时地表温度不确定带来的土壤含水量估算误差。相较于传统的LST-FVC特征空间,DTR-FVC特征空间的土壤含水量反演结果具有更高的精度,证明温度日较差DTR在土壤含水量的反演研究中具有很大潜力。而且DTR-FVC特征空间在土壤含水量较低的区域反演精度更高,更适用于干旱/半干旱地区。
和地表温度-植被指数特征空间法一样,DTR-FVC特征空间法同样难以获取受云影响的像元的土壤含水量。另外,本文只使用了西班牙Duero盆地中部地区的REMEDHUS土壤含水量观测网络对计算结果进行验证,由于天气和站点的原因,一天中可用的实测数据一般在15个以内,有一定的局限性。
| [1] |
Carlson T. An overview of the "triangle method" for estimating surface evapotranspiration and soil moisture from satellite imagery[J]. Sensors, 2007, 7: 1612-1629. DOI:10.3390/s7081612 |
| [2] |
Kidd C, Levizzani V, Bauer P. A review of satellite meteorology and climatology at the start of the twenty-first century[J]. Progress in Physical Geography, 2009, 33(4): 474-489. DOI:10.1177/0309133309346647 |
| [3] |
陈斌, 张学霞, 华开. 温度植被干旱指数(TVDI)在草原干旱监测中的应用研究[J]. 干旱区地理, 2013, 36(5): 930-937. |
| [4] |
刘焕军, 张柏, 宋开山. 黑土土壤含水量光谱响应特征与模型[J]. 中国科学院研究生院学报, 2008, 25(4): 503-509. |
| [5] |
陈书林, 刘元波, 温作民. 卫星遥感反演土壤含水量研究综述[J]. 地球科学进展, 2012, 27(11): 1192-1203. |
| [6] |
胡猛, 冯起, 席海洋. 遥感技术监测干旱区土壤含水量研究进展[J]. 土壤通报, 2013, 44(5): 1270-1275. |
| [7] |
Yuan W, Li Z, Liu N, et al. Passive microwave remote sensing for soil moisture retrieval based on bi-spectrum scattering model[J]. Chinese Journal of Radio Science, 2004, 19(1): 1-6. |
| [8] |
Wigneron J P, Calvet J C, De Rosnay P, et al. Soil moisture retrievals from biangular L-band passive microwave observations[J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 277-281. DOI:10.1109/LGRS.2004.834594 |
| [9] |
Hasan S, Montzka C, Rüdiger C, et al. Soil moisture retrieval from airborne L-band passive microwave using high resolution multispectral data[J]. Isprs Journal of Photogrammetry and Remote Sensing, 2014, 91(5): 59-71. |
| [10] |
Ye N, Walker J P, Guerschman J, et al. Standing water effect on soil moisture retrieval from L-band passive microwave observations[J]. Remote Sensing of Environment, 2015, 169: 232-242. DOI:10.1016/j.rse.2015.08.013 |
| [11] |
Sun L, Sun R, Li X, et al. Monitoring surface soil moisture status based on remotely sensed surface temperature and vegetation index information[J]. Agricultural and Forest Meteorology, 2012, 166: 175-187. |
| [12] |
Lu L, Luo G P, Wang J Y. Development of an ATI-NDVI method for estimation of soil moisture from MODIS data[J]. International Journal of Remote Sensing, 2014, 35(10): 3797-3815. DOI:10.1080/01431161.2014.919677 |
| [13] |
Stisen S, Sandholt I, Nørgaard A, et al. Combining the triangle method with thermal inertia to estimate regional evapotranspiration:applied to MSG-SEVIRI data in the Senegal River basin[J]. Remote Sensing of Environment, 2008, 112(3): 1242-1255. DOI:10.1016/j.rse.2007.08.013 |
| [14] |
Gillies R R. A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover[J]. Remote Sensing Reviews, 1994, 9(1): 161-173. |
| [15] |
Carlson T N. Regional-scale estimates of surface moisture availability and thermal inertia using remote thermal measurements[J]. 1986, 1(2): 197-247. https://www.tandfonline.com/doi/abs/10.1080/02757258609532069
|
| [16] |
Zhang D, Zhou G. Estimation of soil moisture from optical and thermal remote sensing:a review[J]. Sensors, 2016, 16(8): 1308-1337. DOI:10.3390/s16081308 |
| [17] |
Li Z L, Tang R L, Wan Z M, et al. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data[J]. Sensors, 2009, 9(5): 3801-3853. DOI:10.3390/s90503801 |
| [18] |
Moran M S, Clarke T R, Inoue Y, et al. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index[J]. 1994, 49(3): 246-263. https://www.sciencedirect.com/science/article/abs/pii/0034425794900205
|
| [19] |
Carlson T, Buffum M J. On estimating total daily evapotranspiration from remote surface temperature measurements[J]. Remote Sensing of Environment, 1989, 29(2): 197-207. DOI:10.1016/0034-4257(89)90027-8 |
| [20] |
Price J C. Using spatial context in satellite data to infer regional scale evapotranspiration[J]. IEEE Transactions on Geoscience & Remote Sensing, 1990, 28(5): 940-948. |
| [21] |
Nemani R, Pierce L, Running S, et al. Developing satellite-derived estimates of surface moisture status[J]. Journal of Applied Meteorology, 1993, 32(3): 548-557. DOI:10.1175/1520-0450(1993)032<0548:DSDEOS>2.0.CO;2 |
| [22] |
Hansen J, Sato M, Ruedy R. Long-term changes of the diurnal temperature cycle:implications about mechanisms of global climate change[J]. Atmospheric Research, 1995, 37(1): 175-209. |
| [23] |
Kavin E T, Karl T K. Effects of clouds, soil moisture, precipitation and water vapor on diurnal temperature range[J]. Journal of Climate, 1999, 12(8): 2451-2473. DOI:10.1175/1520-0442(1999)012<2451:EOCSMP>2.0.CO;2 |
| [24] |
Zhang D J, Tang R L, Zhao W, et al. Surface soil water content estimation from thermal remote sensing based on the temporal variation of land surface temperature[J]. Remote Sensing, 2014, 6(4): 3170-3187. DOI:10.3390/rs6043170 |
| [25] |
Leng P, Song X N, Duan S B, et al. A practical algorithm for estimating surface soil moisture using combined optical and thermal infrared data[J]. International Journal of Applied Earth Observations and Geoinformation, 2016, 52: 338-348. DOI:10.1016/j.jag.2016.07.004 |
| [26] |
Duan S B, Li Z L, Tang B H, et al. Direct estimation of land-surface diurnal temperature cycle model parameters from MSG-SEVIRI brightness temperatures under clear sky conditions[J]. Remote Sensing of Environment, 2014, 150: 34-43. DOI:10.1016/j.rse.2014.04.017 |
| [27] |
Braganza K, Karoly D J, Arblaster J M. Diurnal temperature range as an index of global climate change during the twentieth century[J]. Geophysical Research Letters, 2004, 31(13): 405-407. |
| [28] |
Carlson T N, Gillies R R, Schmugge T J. An interpretation of methodologies for indirect measurement of soil-water content[J]. Agricultural & Forest Meteorology, 1995, 77(3): 191-205. |
| [29] |
Sandholt I, Rasmussen K, Andersen J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status[J]. Remote Sensing of Environment, 2002, 79(2): 213-224. |
| [30] |
Zhang R H, Tian J, Su H B, et al. Two improvements of an operational two-layer model for terrestrial surface heat flux retrieval[J]. Sensors, 2008, 8(10): 6165-6187. DOI:10.3390/s8106165 |
| [31] |
Verstraeten W W, Veroustraete F, Sande C J, et al. Soil moisture retrieval using thermal inertia, determined with visible and thermal spaceborne data, validated for European forests[J]. Remote Sensing of Environment, 2006, 101(3): 299-314. DOI:10.1016/j.rse.2005.12.016 |
| [32] |
Saxton K E, Rawls W J. Estimating generalized soil-water characteristics from texture[J]. Soil Science Society of America Journal, 1986, 50(4): 1031-1036. DOI:10.2136/sssaj1986.03615995005000040039x |
 2018, Vol. 35
2018, Vol. 35 


