2. 香港城市大学物理及材料科学系, 香港 999077
2. Department of Physics and Materials Science, City University of Hongkong, Hongkong 999077, China
轴承是机械设备中最重要的零部件之一,轴承的好坏关系到机械设备的使用寿命。任何机械、工程结构都不可避免地存在着各种类似于裂纹的缺陷,它们的形成原因多种多样,比如材料固有的缺陷、制造加工过程中造成的损伤、腐蚀造成的损伤和使用过程中疲劳或偶然造成的损伤等。这些缺陷的存在会大大降低结构的承载能力和使用寿命,最终导致结构提前失效。等效应力强度因子是评估裂纹危险程度的重要指标之一。国内外学者就轴承缺陷的实时监测诊断和安全评估等方面开展了大量的工作[1-2]。文献[3]利用主成分分析和支持向量机等统计学方法探索基于轴承振动信号的缺陷诊断方法。文献[4]利用有限元方法研究载荷和旋转角度两个因素对于一种桥梁滚动轴承滚动体上裂纹应力强度因子的影响。研究结果表明裂纹长度比和旋转角度对Ⅰ型应力强度因子和Ⅱ型应力强度因子均有非常大的影响。文献[5-6]利用有限元方法系统地研究不同形状表面裂纹的滚动疲劳扩展规律。文献[7]研究轴承材料缺陷对于滚动接触疲劳裂纹萌生的影响。文献[8-10]利用Franc 3D软件研究摩擦对于轨道滚动接触疲劳裂纹扩展的影响,研究结果表明所受应力、裂纹方向和轨道尺寸等多个因素都影响裂纹扩展的速率。而有关轴承裂纹方向对裂纹扩展速率影响方面的研究未见报道。研究不同方向的轴承裂纹对其应力强度因子的影响能力,可以评估不同方向的裂纹危险程度,这对于研究裂纹方向对于轴承寿命的影响,进而避免由于轴承断裂而造成的事故具有重要的意义。
本文利用有限元方法建立单滚动体和内圈组成的轴承模型,在接触位置建立不同方向的裂纹,研究不同裂纹方向对于裂纹扩展速率的影响能力。
1 模型的建立 1.1 边界条件接触疲劳是轴承破坏的主要形式,因此研究轴承的滚动接触疲劳裂纹扩展问题对开展轴承的滚动接触疲劳损伤容限问题具有重要意义。本文以6205轴承为例,研究内圈滚道上不同方向裂纹对于轴承寿命的影响。利用有限元方法建立由单滚动体和内圈组成的模型(如图 1(a)所示),在滚动体和内圈接触位置建立径向半椭圆裂纹,裂纹的长轴和短轴分别为1.0和0.5mm。边界条件[6-7]为:滚动体当作刚体设为全约束,内圈加载动量500N·s和沿图 1中-x方向径向载荷3kN,并在内圈加圆柱面约束,固定轴向自由度。

|
Download:
|
| 图 1 轴承模型及裂纹网格划分图 Fig. 1 Bearing model and mesh diagram of bearing inner ring crack | |
轴承模型网格划分如图 1(a)所示,单元类型为四面体,其中裂纹局部的网格划分如图 1(b)所示。裂纹部分采用局部细化网格和接触网格划分方法,裂尖附近网格尺寸为0.02mm。为节省计算时间,其余部分采用自由网格划分方法。
1.3 模型裂纹与内圈轴向夹角α为椭圆裂纹短轴在yoz面上的投影与z轴的夹角。裂纹与内圈径向夹角θ为椭圆裂纹短轴在xoy面上的投影与x轴的夹角。轴承所用材料为GCr15,热处理工艺为:加热到860℃保温20min油淬,再经过180℃回火保温2h后空冷。热处理后杨氏模量为210GPa,泊松比取0.3,断裂韧性为42.8MPa·m0.5。
Paris和Erdogan[11]提出裂纹扩展速率与应力强度因子幅值有关,并提出公式(1)描述裂纹扩展速率与应力强度因子幅值之间的关系:
| $ \frac{{{\rm{d}}L}}{{{\rm{d}}N}} = C{(\Delta K)^n}, $ | (1) |
式中:ΔK为应力强度因子的幅值;L为裂纹长度;N为经历载荷的周次;C和n为与材料相关的常数。从式(1)可以看出裂纹扩展速率与等效应力强度因子的幅值密切相关。因此,本文利用有限元方法建立单滚动体和内圈组成的轴承模型,在接触位置建立不同方向的裂纹,研究裂纹的等效应力强度因子的变化规律。
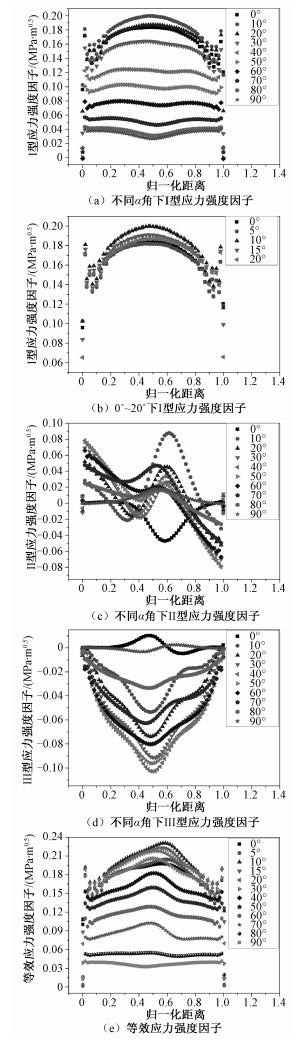
2 仿真分析 2.1 裂纹与内圈轴向夹角α对应力强度因子的影响半椭圆裂纹的中心为接触点,以垂直于滚动体滚动方向为0°,逆时针方向为正,应力强度因子通过位移外推法获得。探索0°~90°之间以10°为间隔的应力强度因子变化。图 2(a)为不同α角下裂尖Ⅰ型应力强度因子的变化。从结果中可以看出,10°下裂尖的Ⅰ型应力强度因子相对较大,90°下裂尖的Ⅰ型应力强度因子相对较小,且0°和20°下裂尖的Ⅰ型应力强度因子数值相近,20°~90°之间裂尖的应力强度因子呈下降趋势。为探索最大应力强度因子的角度,在0°~20°范围内对裂尖应力强度因子的求解角度间隔进行细化(图 2(b))。从图中可以看出,最大应力强度因子仍旧出现在10°左右。这说明倾斜角为10°左右的裂纹扩展扩展速率更快,对轴承的破坏能力更强。
|
Download:
|
| 图 2 不同α角下应力强度因子随裂纹前沿归一化距离的变化 Fig. 2 Variation in stress intensity factor(SIF) with the normalized distance at different α values | |
图 2(c)为不同α角下裂尖Ⅱ型应力强度因子的变化。从图中可以看出,裂纹Ⅱ型应力强度因子最大值也出现在10°左右。图 2(d)为不同α角下裂尖Ⅲ型应力强度因子的变化。从图中可以看出,在0°~40°范围内应力强度因子随着角度的增加呈增大趋势,而在50°~90°范围内相同归一化位置的应力强度因子随着角度的增加呈减小趋势,且在40°和50°范围内应力强度因子基本一致,这说明在45°左右Ⅲ型应力强度因子最大,即45°角最容易发生Ⅲ型断裂。
裂纹角度在0°~20°之间,Ⅰ型和Ⅱ型应力强度因子均存在最大值。Ⅰ型裂纹在20°~90°之间呈下降趋势,而Ⅱ型裂纹在此区间内先上升后下降,且在40°~50°之间有极值存在。Ⅲ型应力强度因子随角度增加先上升后下降,且在40°~50°之间有极值存在。考虑到上述裂纹是三维裂纹,这就需要等效应力强度因子来评价裂纹扩展速率。等效应力强度因子[5]可以表达为
| $ {K_{{\rm{eff}}}} = \sqrt {K_{\rm{I}}^2 + K_{{\rm{II}}}^2 + \frac{{K_{{\rm{III}}}^2}}{{1 - \nu }}} . $ | (2) |
利用式(2)获得不用α角下等效应力强度因子如图 2(e)所示。等效应力强度因子的最大值为0.22MPa·m0.5,出现在10°左右。当裂纹方向平行于滚动体滚动方向,即角度为90°时,等效应力强度因子最小,仅为0.039MPa·m0.5。这说明裂纹方向对等效应力强度因子的影响作用显著。且倾斜角为10°左右的裂纹扩展扩展速率最快,对轴承的破坏能力最强。文献[12]研究表面初始裂纹的接触疲劳扩展规律,利用实验的方法观察裂纹的扩展路径,从其裂纹扩展路径中可以看出初始裂纹呈V型扩展,虽然文献[12]中未给出准确的角度,但是通过对裂纹扩展图像进行观察发现,其倾斜角相对较小。这与本文得到的结果相吻合。
2.2 裂纹与内圈径向夹角θ对应力强度因子的影响利用workbench在滚动体和内圈接触位置建立与内圈径向成一定夹角的半椭圆裂纹,裂纹的长轴和短轴分别为1.0和0.5mm。半椭圆裂纹的中心为接触点,以平行于径向的方向为0°,逆时针方向为正。探索-80°~80°之间以10°为间隔的应力强度变化。
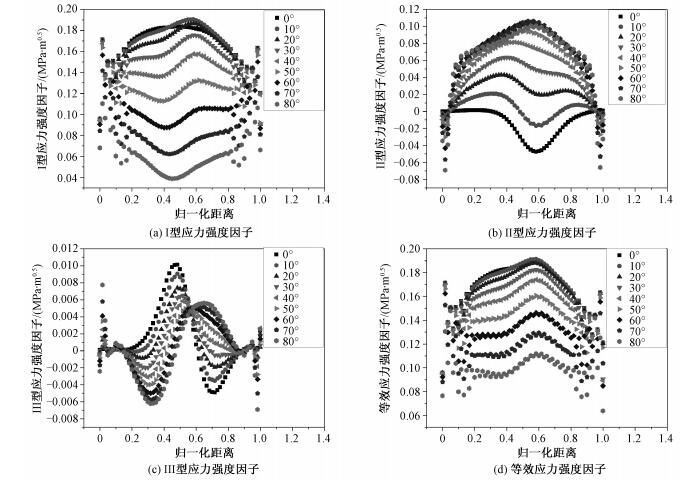
图 3(a)为0°~80°之间裂尖Ⅰ型应力强度因子的变化,从图中可以看出0°~20°之间裂尖Ⅰ型应力强度因子的变化幅度不大,而在20°~80°之间裂尖Ⅰ型应力强度因子明显随着角度的增加而减小。从最大应力强度因子所出现的归一化距离来看,在45°之内最大应力强度因子出现在0.6左右,而大于45°的区域其最大应力强度因子出现在裂尖边缘。图 3(b)为0°~80°之间裂尖Ⅱ型应力强度因子的变化图。从图中可以看出,夹角为70°时应力强度因子相对较大,在0°~60°之间随着角度的增加应力强度因子变大。图 3(c)为不同θ角下Ⅲ型应力强度因子的变化。从图中看出Ⅲ型应力强度因子相对较小,在这里不做详细讨论。不同θ角下等效应力强度因子的分布情况如图 3(d)所示。等效应力强度因子在0°~20°之间相对较大,在20°~80°之间随着角度的增加逐渐减小。等效应力强度因子的最大值为0.19MPa·m0.5,最小值为0.11MPa·m0.5。说明裂纹与内圈径向夹角θ对应力强度因子的影响能力较夹角α对应力强度因子的影响能力弱。夹角θ为0°~20°之间的裂纹相对其他角度裂纹可以更快地扩展,即相对较危险。
|
Download:
|
| 图 3 在0°~80°之间不同θ角下应力强度因子随裂纹前沿归一化距离的变化 Fig. 3 Variation in stress intensity factor(SIF) with the normalized distance at different θ values from 0° to 80° | |
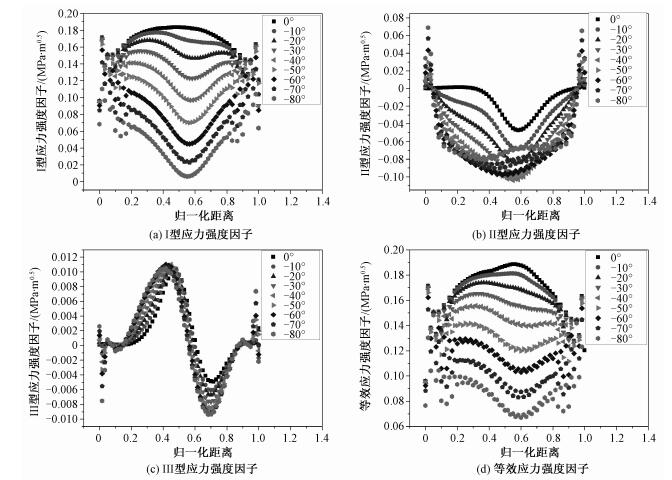
图 4(a)为-80°~0°之间裂尖Ⅰ型应力强度因子的变化,从图中可以看出应力强度因子随着角度的减小呈下降趋势,这说明角度越小其裂纹扩展的速率越慢,即径向裂纹的危害性最大。对于Ⅱ型应力强度因子(如图 4(b)所示),0°下应力强度因子最小,-30°~0°之间随着角度增加应力强度因子变小,剩余角度下应力强度因子的变化较小。与0°~80°之间Ⅲ型应力强度因子相似(如图 4(c)所示),考虑到其数值较小,在这里不做讨论。图 4(d)为不同θ角下等效应力强度因子变化图。从图中可以看出,等效应力强度因子随着角度从-80°增大到0°而逐渐增大。这说明角度在-80°~0°之间的裂纹随着角度的增加裂纹扩展速率逐渐增大,在0°左右达到最大值。
|
Download:
|
| 图 4 在-80°~0°之间不同θ角下应力强度因子随裂纹前沿归一化距离的变化 Fig. 4 Variation in stress intensity factor(SIF) with the normalized distance at different θ values from -80° to 0° | |
综合上述研究结果,得到裂纹与内圈径向夹角θ在-80°~80°之间裂尖等效应力强度因子最大值随角度变化关系图(图 5)。从图中可以看出,等效应力强度因子最大值出现在10°左右,可达0.19MPa·m0.5;最小值出现在80°和-80°左右,均小于0.15MPa·m0.5。角度在10°~80°范围内下降速率明显大于10°~-80°的下降速率,说明10°~80°范围内角度对等效应力强度因子的影响较大。这表明夹角10°左右的裂纹危险程度最大,日常维护中要特别注意。文献[12]研究表面初始裂纹的接触疲劳扩展规律,利用实验的方法观察裂纹的扩展路径,从其裂纹扩展路径中可以看出初始裂纹扩展的方向与内圈径向是有一定夹角的,这与本文得到的结果吻合。另一方面,文献[10]中研究表明沿滚动体滚动方向的裂纹更加危险,这也与本文的结论相吻合。

|
Download:
|
| 图 5 裂尖等效应力强度因子随θ角度变化 Fig. 5 Variation in equivalent stress intensity factor with θ angle | |
1) 裂纹方向对裂纹扩展速率影响较大。当裂纹与内圈轴向夹角α在10°左右时,等效应力强度因子出现最大值,其值为0.22MPa·m0.5;夹角在90°左右时,等效应力强度因子出现最小值,其值为0.039MPa·m0.5,仅约为夹角为10°时等效应力强度因子的1/5。
2) 当裂纹方向与内圈径向夹角θ在10°左右时,等效应力强度因子出现最大值0.19MPa·m0.5;夹角在80°和-80°左右时,等效应力强度因子出现最小值0.15MPa·m0.5。
3) 裂纹与内圈轴向夹角α对裂纹扩展速率的影响明显大于裂纹方向与内圈径向夹角θ对其的影响,因此在日常检查中不仅要关注裂纹形状的检查,还要特别注重裂纹方向的检查。本研究对于评估不同方向裂纹的危害程度有重要的参考价值。
| [1] |
Ali J B, Chebel-Morello B, Saidi L, et al. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network[J]. Mechanical Systems and Signal Processing, 2015, s 56/57: 150-172. |
| [2] |
Rai A, Upadhyay S H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings[J]. Tribology International, 2016, 96: 289-306. DOI:10.1016/j.triboint.2015.12.037 |
| [3] |
Dong S, Sun D, Tang B, et al. A fault diagnosis method for rotating machinery based on PCA and morlet kernel SVM[J]. Mathematical Problems in Engineering, 2014, 2014(10): 1-8. |
| [4] |
Noury P, Eriksson K. Determination of stress intensity factors for cracked bridge roller bearings using finite element analyses[J]. Engineering Fracture Mechanics, 2017, 169: 67-73. DOI:10.1016/j.engfracmech.2016.10.018 |
| [5] |
Deng S, Hua L, Han X, et al. Analysis of surface crack growth under rolling contact fatigue in a linear contact[J]. Tribology Transactions, 2015, 58(3): 432-443. DOI:10.1080/10402004.2014.983250 |
| [6] |
Deng S, Qin X, Huang S. A study on the effect of subsurface crack propagation on rolling contact fatigue in a bearing ring[J]. Journal of Mechanical Science and Technology, 2015, 29(3): 1029-1038. DOI:10.1007/s12206-014-1114-2 |
| [7] |
Hua L, Deng S, Han X, et al. Effect of material defects on crack initiation under rolling contact fatigue in a bearing ring[J]. Tribology International, 2013, 66: 315-323. DOI:10.1016/j.triboint.2013.06.008 |
| [8] |
Nejad R M. Using three-dimensional finite element analysis for simulation of residual stresses in railway wheels[J]. Engineering Failure Analysis, 2014, 45(1): 449-455. |
| [9] |
Nejad R M, Farhangdoost K, Shariati M. Numerical study on fatigue crack growth in railway wheels under the influence of residual stresses[J]. Engineering Failure Analysis, 2015, 52: 75-89. DOI:10.1016/j.engfailanal.2015.03.002 |
| [10] |
Nejad R M, Shariati M, Farhangdoost K. Effect of wear on rolling contact fatigue crack growth in rails[J]. Tribology International, 2016, 94: 118-125. DOI:10.1016/j.triboint.2015.08.035 |
| [11] |
Paris P C, Erdogan F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4): 528-533. DOI:10.1115/1.3656900 |
| [12] |
Rycerz P, Olver A, Kadiric A. Propagation of surface initiated rolling contact fatigue cracks in bearing steel[J]. International Journal of Fatigue, 2017, 97: 29-38. DOI:10.1016/j.ijfatigue.2016.12.004 |
 2018, Vol. 35
2018, Vol. 35 


