随着计算技术的发展，计算机仿真试验在科学与工程中的应用越来越广^[1-3]。由于仿真试验通常比较耗时，因此计算机试验和传统物理试验一样，需要有效地挑选少量试验点来进行仿真^[4-6]。计算机试验的设计一般采用空间填充设计^[7-11]，其核心思想是设计点应在试验区域内分布得尽量均匀。常用的一类空间填充设计是最大最小距离设计^[10-18]。其定义如下：点$D = \{ {x_1}, \ldots , {x_n}\} $称为空间[0, 1]^d, d∈Z⁺中的最大最小距离设计如果它是优化问题$ \mathop {{\rm{max}}}\limits_{{x_1}, \ldots , {x_n}} \mathop {{\rm{min}}}\limits_{1 \le i < j \le n} \parallel i - {x_j}\parallel , {\rm{s}}{\rm{.t}}{\rm{.}}\;{x_1}, \ldots , {x_n} \in {\left[ {0, 1} \right]^d}, d \in {Z^ + }$的解，其中‖·‖代表欧式距离^[2]。最大最小距离设计也可以做成序贯类型^[19]，即按照最小距离准则一个个地增加试验点，这样就可以用较少的试验点得出结论，也可避免盲目加大样本数而造成浪费。文献[6]给出了其具体的定义。如今，已有不少文献讨论过最大最小距离设计的性质和构造，如文献[10-18]，但目前还没有文章对序贯最大最小距离设计的性质进行讨论。本文将讨论序贯最大最小距离设计的空间填充性质。证明序贯最大最小距离设计满足最基本的空间填充性，即随着样本量的增大，该设计在试验区域内具有稠密性，可以任意逼近试验区域内的任意一个点。

1 构造序贯最大最小距离设计

在[0, 1]^d, d∈Z⁺中，按如下规则取点：使新取的点到所有已取点的最小距离最大化。引入下列记号表示：

记前n步取的点分别为$ {s_1}, {s_2}, \ldots , {s_n}, {S_n} = \{ {s_1}, {s_2}, \ldots , {s_n}\} $为前n步取点的点集，

1) 记任意两点x, y∈[0, 1]^d间的距离为d(x, y)=‖x-y‖₂。

2) 记任意一点x∈[0, 1]^d到已选点集合S_n的距离$ d(x, {S_n}) = \mathop {{\rm{min}}}\limits_{{s_i} \in {S_n}} \{ d(x, {s_i})\} $。

3) 下一步要寻找的点$ {s_{n + 1}} = \mathop {\arg \max }\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_n})\} $，记${q_n} = \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_n})\} $。

按上述规则，在[0, 1]²中，依次规定取点个数画图。

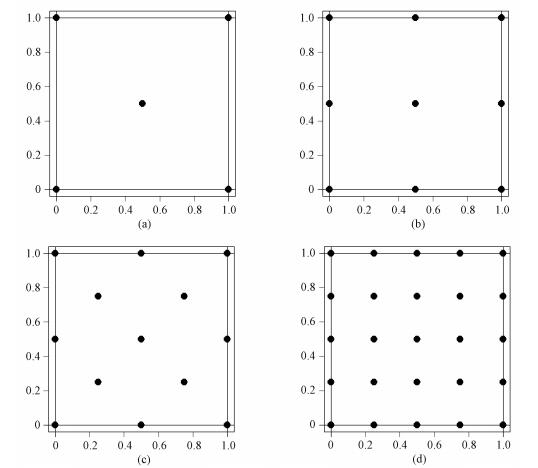
图 1中，当在[0, 1]²中第1次取点时，因为此时[0, 1]²中不存在点，规定取的第1个点在正方形的中心。接下来就可以按照序贯最大最小距离设计在空间中依次取点。第2次取点时，有4个点同时满足规则，它们在正方形的4个顶点处。可以看出，按序贯最大最小距离设计取点，可以将[0, 1]²逐步填充。

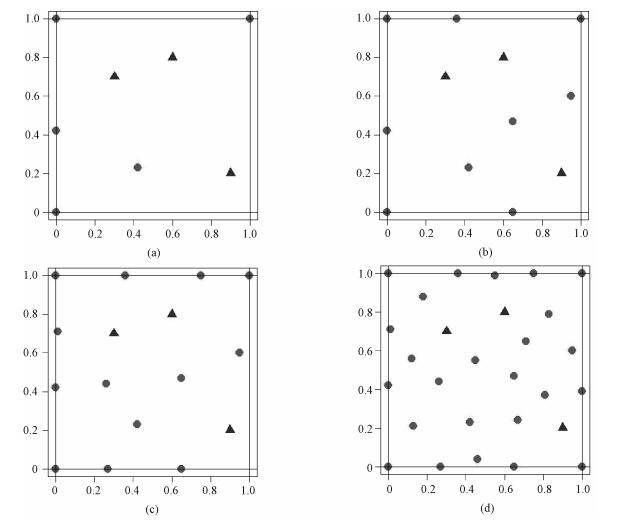
图 2中，一开始[0, 1]²中已经取了3个点，这3个点用三角形表示，再按序贯最大最小距离设计取点，取得的点用圆形表示。可以看出，这种情况下序贯最大最小距离设计也可以对[0, 1]²进行逐步填充。

2 主要结果及证明

从第1节可以看出，随着样本量的增加，序贯最大最小距离设计可以对2维试验区域进行逐步填充。下面对任意的维数严格证明这一性质。

定理2.1  在[0, 1]^d, d∈Z⁺中，按序贯最大最小距离设计取点，设所取得的点依次为$ {s_1}, {s_2}, \ldots , {s_n}$，则对任意ε>0，任意x∈[0, 1]^d，都存在一个N>0，当n>N时，有d(x, S_n) < ε。

证明  反证方向为：存在ε>0，存在一个x₀∈[0, 1]^d，对任意的N₁>0，都存在一个N₂>N₁，有d(x₀, S_N2)≥ε。

继续使用第1节中的符号。根据取点方式：$ {s_{n + 1}} = \mathop {\arg \max }\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_n})\} $，记$ {q_n} = \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_n})\} $，

则有

$ \begin{array}{l} {q_{n + 1}} = \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_{n + 1}})\} \\ = \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} {\rm{ }}\{ \mathop {{\rm{min}}}\limits_{{s_i} \in {S_{n + 1}}} d(x, {S_{n + 1}})\} \\ = \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} {\rm{ }}\{ \mathop {{\rm{min}}}\limits_{{s_i} \in {S_n}} \{ {\rm{min}}d(x, {S_n}), d(x, {s_{n + 1}})\} \} \\ \le \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_n})\} = {q_n}. \end{array} $

故集合{q_n}_{n=1, 2, …}是一个单调递减的集合，且由定义有q_i≥0，故集合有下确界，记$a = \mathop {{\rm{inf}}}\limits_{n = 1, 2, \ldots } \{ {q_n}\} $为其下确界，易得a≥0。

由反证法假设，存在ε>0，存在一个x₀∈[0, 1]^d，对任意的N₁>0，都存在一个N₂>N₁，有d(x₀, S_N2)≥ε，则${q_{{N_2}}} = \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_{{N_2}}})\} \ge \varepsilon $。

即存在ε>0，对任意的N₁>0，都存在一个N₂>N₁，使得q_N2≥ε>0，且{q_n}_{n=1, 2, …}单调递减，故可以得a≥ε>0。

下面证明对于任意已取得的点${s_i}, {s_j} \in {S_{{N_2}}} $，均有$d({s_i}, {s_j}) \ge a > 0 $，证明如下：

已知$ {s_{n + 1}} = \mathop {\arg \max }\limits_{x \in {{\left[ {0, 1} \right]}^d}} {\rm{ }}\{ d(x, {S_n})\} , {q_n} = \mathop {{\rm{max}}}\limits_{x \in {{\left[ {0, 1} \right]}^d}} \{ d(x, {S_n})\} = d({s_{n + 1}}, {S_n}) \ge a$，则对任意i≥2，均有d(s_i+1, S_i)≥a。

对于反证条件中任意的N₁>0，取${N_2} = {N_1} + \left\lceil {\frac{{{{(1 + {d^{1/2}})}^d}\Gamma \left( {d/2 + 1} \right)}}{{{{\rm{ \mathsf{ π} }}^{d/2}}{{\left( {a/2} \right)}^d}}}} \right\rceil + 1 > {N_1} $，则若存在$ {s_i}, {s_j} \in {S_{{N_2}}}$使得$ d({s_i}, {s_j}) < a$, 不妨设i > j，则${s_j} \in {S_{i - 1}} $，则有$d({s_i}, {S_{i - 1}}) = \mathop {{\rm{min}}}\limits_{x \in {S_{i - 1}}} \{ d({s_i}, x)\} \le d({s_i}, {s_j}) < a $。与$ d\left( {{S_i}, {S_{i - 1}}} \right) \ge a$矛盾，所以我们证明出对于任意已取得的点$ {s_i}, {s_j} \in {S_{{N_2}}}$，均有$ d({s_i}, {s_j}) \ge a > 0$，所以对S_N2中所有的点以$ \frac{a}{2}$为半径做球，球两两不相交。这N₂个球的体积和为${N_2}\cdot{{\rm{ \mathsf{ π} }}^{d/2}}{\left( {a/2} \right)^d}/\Gamma \left( {d/2 + 1} \right) > {(1 + {d^{1/2}})^d} $。

但由于在空间[0, 1]^d中，任意两点间的最大距离不超过d^1/2，故每个球的半径应满足

$ \frac{a}{2} \le \frac{{{d^{1/2}}}}{2}, $

且球心均在[0, 1]^d中，所以所有的球一定被完全包含在$ {\left[ { - \frac{{{d^{1/2}}}}{2}, 1 + \frac{{{d^{1/2}}}}{2}} \right]^d}$中，且这N₂个球不相交，故N₂个球的体积和一定满足

$ {V_{{\rm{qiu}}}} < {(1 + {d^{1/2}})^d}, $

这与${N_2}\cdot{{\rm{ \mathsf{ π} }}^{d/2}}{\left( {a/2} \right)^d}/\Gamma \left( {d/2 + 1} \right) > {(1 + {d^{1/2}})^d} $矛盾。

故原假设不成立，即我们证明了：对任意ε>0，任意x∈[0, 1]^d，都存在一个N>0，当n>N时，均有d(x, S_n) < ε。即按序贯最大最小距离设计多次取点，可以填充空间[0, 1]^d。

注1  上面证明的是[0, 1]^d中一开始没有取任何点时，按照序贯最大最小距离设计取点，可将[0, 1]^d填充。这个时候第1个点放在空间的中心，第2个点就应该取在空间[0, 1]^d的一个顶点处。

若[0, 1]^d中一开始存在k个点${t_1}, {t_2}, \ldots , {t_k} $，再在空间中按序贯最大最小距离设计取点时，依然可以证明定理成立。第1次取点时，需要使新点到这k个点的最小距离最大，第2次取点时，需要使新点到这k+1个点的最小距离最大……因此在证明时，应使点集S_i, i=1, 2, …中都包含这k个点。取$ \begin{array}{l} c = {\rm{min}}\{ \parallel {t_i} - {t_j}\parallel , i, j = 1, 2, 3, \ldots , k, i \ne j\} , b = {\rm{min}}\left\{ {a, c} \right\} \end{array}$，在证明一开始将ε取得足够小使得c>ε，就可保证b>ε，再以$ \frac{b}{2}$为半径以S_N2中的所有点为球心做球，且将N₂表达式中的a全部替换为b，也可得定理结论成立。

注2   上述定理证明的是序贯最大最小距离设计对[0, 1]^d的填充性，同样地，对任一d维紧集，在空间中一开始已经取了点和没取点两种情况下，仍能证明按序贯最大最小距离设计取点可将空间填充。