2. University of Chinese Academy of Sciences, Beijing 100049, China
2. 中国科学院大学, 北京 100049
In the context of global warming, a lot of the world's small mountain glaciers are losing mass at an accelerated rate, which causes a rise in sea level[1]. Much effort has been made to develop various methods to estimate the amount of glacier ablation throughout the world[2]. In these methods, degree-day model was considered to be the most common approach for melt modelling due to its simplicity and good performance[3]. The model depends on an assumed relationship between ablation and air temperature, which is expressed, in general, in the form of positive mean daily temperature sum. Degree-day factor (hereafter, DDF), being the factor of proportionality, represents the glacier ablation for a unit positive degree-day[4]. It simplifies the complex physical processes that are more properly described by energy balance models, which means that the factor itself has a certain physical mechanism. Accordingly, there is various in DDF caused by the energy partitioning with different seasons and spatial locations[5]. Several studies have proved that the seasonal variation in DDFs of glaciers can be ignored for its no significant[3, 6]. However, a large difference of DDFs in the spatial distribution was revealed[7], which greatly affect the accuracy of glaciers melt model[3].
In general, the DDF can be derived from measurement of ablation stick[8], as well as calculation by energy balance model[7]. In the Yarlung Zangbo River Basin (hereafter, YZRB), characterized by high altitude and extreme topographical conditions[9], direct and continuous measurements of DDFs are not available due to the inaccessibility of glaciers and the logistical difficulties associated with maintaining a DDF record. Energy balance model is characterized by complex physical processes, which results difficulties in application due to the restricted data availability in this basin. In order to improve the accuracy of runoff yield in the glacierized basin for distributed hydrologic model, a proper algorithm need to be developed to generate a distributed DDF map of glaciers scale in YZRB on moderate resolution (1 km).
With different topography (i.e. elevation, slope, aspect, latitude and longitude) and heat fluxes, DDFs will vary considerably in spatial distribution[10]. In general, the DDFs are considered to be positive correlation with elevation and direct solar radiation input, but negative correlation with sensible heat flux[3]. Pre-existing study suggested that high shares of sensible heat flux, resulting from high air temperature and wind speed, usually associated with low DDFs[11]. It is well known that air temperature has a strong relationship with topography. Therefore, a multiple regression equation with statistical optimum choosing between observed DDFs of different glaciers around the YZRB and topographic factors is established to produce distributed DDFs in YZRB, and the method of improved neighborhood mean filtering is used to revise some abnormal pixels in DDFs map in this study.
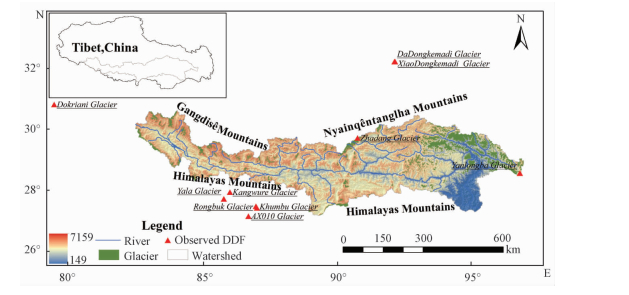
1 Study areaOriginating from the Chemayungdung Glacier in the northern slope with an average elevation of 4 600 m. a.s.l. over the Himalayas, the River in YZRB is the highest river on the earth stretching across the south part of the Tibetan Plateau from the west to the east with total length of about 2 057 km, a drainage area of about 257 680 km2[9, 12]. Geographically, the YZRB is situated between 82°1′-97°6′E and 27°49′-31°17′ N (Fig. 1), encompassing a narrow strip with the east-west length exceeding the north-south width, stretching northward to Gangdisê Mountains and the Nyainqêntanglha Mountains and southward to the Himalayas, where about 41 countries (cities) located. The YZRB is a part of Indian Ocean water system. Because of its special geographic location in the Yarlung Zangbo Suture Zone, contributing to the moisture movement from the Indian Ocean to the inner regions of the Qinghai-Tibet Plateau, the YZRB has a significant effect on the rainfall amount of Qinghai-Tibet Plateau[13]. The annual precipitation has an obvious east-west declining gradient from above 2 000 mm to less than 300 mm for the decaying effect of the monsoon[14]. In this basin, there are 10 816 glaciers that covers about 14 493 km2 in area and 1 293 km3 in ice volume, accounting for 29% of the total number of glaciers (36 918) on the Qinghai-Tibet Plateau, as well as 23% of the glacial total in China[15].
|
Download:
|
|
Fig. 1 Fundamental geographic information of Yarlung Zangbo River Basin and the observed DDFs of glaciers around this basin |
|
Due to sparse data availability in the west of China, some short-term observed value of DDFs in different glaciers were collected from literatures and measurement obtained by ourselves in the Yanlongba glacier, the DDFs of ten glaciers around the YZRB were calculated, which was summarized in Table 1 and their geographic locations were shown in Fig. 1.
|
|
Table 1 The average DDFs for different glaciers |
Topography information is important to estimate spatial distribution of ice-DDFs in this paper. Shuttle Radar Topography Mission (SRTM) was hosted by U.S. National Aeronautics and Space Administration (NASA), U.S. National Geospatial-Intelligence Agency (NGA), German Aerospace Center (DLR) and Italian Space Agency (ASI). The version 4 of SRTM DEM (digital elevation model) used in this research is seamless. The DEM data, covering the scope of 60°N-56°S, includes three levels in resolutions, at 1 000, 90 and 30 m, respectively. The spatial resolution of 1 000 m, called moderate resolution image from the aspect of remote sensing technology, is adopted in this paper, which involves two points: one is that the specified resolution of DDFs is enough for simulating runoff in YZRB, the other is that it can properly reduce heterogeneity of underlying surface in DDFs of glaciers. With the 1 000 m resolution of DEM data, ArcGIS software is used to calculate elevation, latitude, longitude, aspect and slope, constituting the topography data in the YZRB.
In addition, the datasets of first Glacier Inventory of China (CGI) derived from Cold and Arid Regions Science Data Center (WestDC)[10] was used as the extent of glaciers in YZRB.
3 Methodology 3.1 Definition and calculation of glacier DDFDDF is defined as the ratio between the amount of glacier ablation and the positive accumulated temperature in the same period[20]. Therefore, the amount of glacier ablation in a specific period can be expressed as
| $ {k_{\rm{g}}} = \frac{{{A_{\rm{g}}}}}{{{\rm{PD}}{{\rm{D}}_{\rm{g}}}}}, $ | (1) |
where kg stands for the glacier DDF (mm·d-1·℃-1); Ag denotes the amount of glacier ablation (mm w. e.), which is obtained by the difference of two measurements using sighting rod multiply by the glacier density (~900 kg·m-3)[21]; PDDg represents the positive accumulated temperature in a certain period (℃). The PDDg can be described as
| $ {\rm{PD}}{{\rm{D}}_{\rm{g}}} = \sum\limits_{t = 1}^n {{H_t} \times {T_t} - {\rm{PD}}{{\rm{D}}_{\rm{s}}}.} $ | (2) |
where Tt denotes the daily mean temperature (℃); Ht, a logical variable, is 0 when the Tt is negative value and is 1 when Tt is positive value. PDDs stands for the positive accumulated temperature used for snow-melt. It is important to keep in mind that PDDs is equal 0 when there is no snow cover on the specific glacier-cover pixel, and the positive accumulated temperature is first used for snow-melt and then for the glacier-melt[16]. However, the measurements data in the field are the total mass balance and accumulation, therefore, the total ablation of glacier and snow is obtained, which leads to the fact that the PDDs and PDDg can not be separated in the total positive accumulated temperature. Therefore, actually the calculated kg based on measurements data is the integrated DDF of snow and glacier[16].
3.2 Estimation of the distributed glacier DDFsThe stepwise regression is widely used in climate and environment prediction for its low computational load and effective variable selection[22-23], which was introduced into estimation of spatial ice-DDFs in this study. In an actual application, the dependent variable DDF was selected as a function of parts or all of independent variables that included elevation, latitude, longitude, slope and aspect. The concrete procedure of stepwise regression was entering one variable at a time into the independent variable set (hereafter, x-set) according to the influence degree of independent variable on dependent variable, and the previous variable in x-set would be removed if it became not significant for dependent variable resulting from a new variable entering. This process would end when no available variables satisfying the tolerance criterion remains or when the reduction in the residual sum of squares failed to exceed a specified threshold[24].
According to previous study, the minimum DDF of glaciers in western China was 2.6 mm·d-1·℃-1[10], and maximum value 16.9 mm·d-1·℃-1 referring to Table 1. Therefore, the value of DDFs derived by stepwise regression without this range was considered to be abnormal pixels (hereafter, it was defined as outliers). Aiming to correct outliers in DDFs and keep normal value unchanged, the method of improved neighboring mean filtering[25] was applied in this paper. The specific process of the improved neighboring mean filtering was shown in Fig. 2. In this proposed algorithm, only the outliers were processed as
| $ \left\{ \begin{array}{l} {O_{{\rm{DDF}}}} = \sum\limits_{i = 1}^n {\frac{{{N_{{\rm{DDF}}}}}}{n}\;\;\left( {n > 0} \right)} \\ {\rm{Next}}\;{\rm{Outlier}}\;\;\;\left( {n = 0} \right) \end{array} \right.. $ | (3) |

|
Download:
|
|
Fig. 2 Flowchart of the neighboring mean filtering improved in this work |
|
where ODDF stands for corrected result of the current outlier by calculating the mean of normal neighboring DDFs, NDDF the normal neighboring DDF and n the number of normal pixels. The pixel will be skipped if the number of normal DDFs is equal to 0 and recalculated in next iteration. It should be noted that the 5×5 filtering window is selected allowing for the area of single glacier.
4 ResultsWith the method of stepwise regression, variables of longitude, slope and aspect in topographical factors were excluded because they were not significant in regression model. The multiple linear regression model between DDFs and significant topographical factors was shown in Equation (2) (r2=0.8) and it was significant at the level of 0.01. Many studies have already shown that higher elevation, in general, results in higher DDFs[2-3, 10]. In addition, Jones[26] argued that there was large difference in melting rate at various altitude and latitude, which indicated that the DDFs have strong relationship with elevation and latitude. These related studies all proved the reasonability of Equation (4).
| $ {\rm{DDF = 0}}{\rm{.009}} \times {\rm{ELE}} - 0.934 \times {\rm{LAT}} - 8.1. $ | (4) |
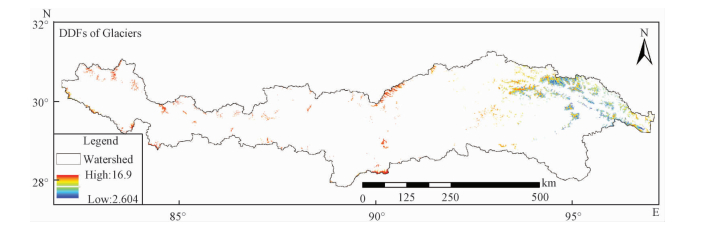
The final spatial distribution of DDFs in YZRB was shown in Fig. 3. Actually, in order to get the result, there were three steps included: the first step was to calculate the preliminary DDFs in YZRB using stepwise regression method. The second step was that the DDFs in glacial extent was extracted with the first Glacier Inventory of China (CGI). The last step was to revise the incorrected DDFs by the algorithm of improved neighboring mean filtering. Due to lack of observed glacial DDFs, direct validation for this result seemed to be difficult. Fortunately, previous study showed that higher snow line usually means larger negative glacial mass balance[15], as well as larger glacial DDF. In order to validate the reliability of this result, the mean DDF and snow line in different orientations of glaciers (Table 2) were calculated by ArcGIS software and derived from Yao et al[15], respectively. The correlation coefficient between DDFs and snow lines in different orientations was up to 0.82 (p < 0.05), which suggested that the DDFs produced in this paper was reasonable for the application in hydrology.
|
Download:
|
|
Fig. 3 Spatially distributed DDFs of glaciers in YZRB |
|
|
|
Table 2 Mean DDFs and snow lines in the different orientations |
From Fig. 3, we could find that DDFs in downstream of YZRB was lower than that in midstream and upstream. One of possible explanations was that there were less precipitation and more solar radiation in upstream and midstream compared to downstream. According to the result of DDFs, the average value of glacial DDFs over YZRB was 10.97 mm·d-1· ℃-1, which could be used as a reference for some applications of cryosphere and hydrology.
5 DiscussionThe DDFs data produced in this study is proven to be reasonable in the different glacier orientations by indirect validation method. However, in addition to the influence of terrain factors presented in this study (i.e. elevation, longitude, latitude, aspect, and slope), the DDF will also be affected by the conditions such as mountain sheltering, wind speed, and solar radiation[16, 21], therefore, no doubt errors do exist in the distributed glacier DDFs data, which may also result from few observed samples, simple regression model, spatial scale, and the neglected seasonal fluctuation. Still, it is very significant to study on this in the ungauged basin under the development of the distributed hydrological modeling, but it requires further studies on the accurate estimation of the distributed glacier DDF in future.
A follow-up study will make an attempt at retrieval of the distributed glacier DDFs based on remotely sensed data. The monthly glacier mass change can be computed by GRACE (gravity recovery and climate experiment) data, which is described detailedly in these literatures[27-28]. Then the monthly distributed glacier DDFs can be obtained with the combination of the glacier mass change and positive accumulated temperature. In addition, the distributed snow DDFs also can be computed by snow water equivalent (SWE) change, which was derived from the special sensor microwave/imager (SSM/I) and scanning multi-channel microwave radiometer (SMMR)[29], and the positive accumulated temperature. This is a preliminary idea of using remotely sensing (RS) data to produce the distributed glacier/snow DDFs, therefore, further studies need to be done in future. Also, the RS-based glacier DDFs can provide an opportunity to make a comparison with the distributed glacier DDFs presented in this study.
6 ConclusionBecause of insensitivity to time dimension, DDFs were only considered to change in spatial distribution. In this study, observed glacial DDFs were collected from literatures and measurement around YZRB. Topographical factors, including elevation, longitude, latitude, aspect and slope derived from SRTM DEM, were fully taken into account in spatial variability of DDFs. With the method of stepwise regression and the datasets of CGI, distributed DDFs were produced in the glacial extent of YZRB by regression model, as well as correction of outliers through improved neighboring mean filtering proposed in this study. The result was indirectly validated by snow lines in different orientations due to lack of available glacial DDFs for validation, which indicated that the reliability of produced DDFs was comparable because the correlation coefficient between snow lines and mean DDFs was up to 0.82.
In the YZRB, DDFs in downstream was lower than that in upstream and midstream, one of possible explanations could be that there were drier and more solar radiation in upstream and midstream compared to downstream influenced by monsoon from India Ocean. According to the result of DDFs, the mean value of DDFs in glacial extent of YZRB was 10.97 mm·d-1·℃-1, which was important to cryosphere and hydrology, especially in the region of sparse data availability.
The spatial dataset in DDFs was produced in this paper, and it was very significant in the distributed hydrological model. However, owning to little studies focusing on the variability of DDFs in the western China, especially in high-mountain regions, future studies on validation of this result are still needed.
| [1] |
Sirguey P, Still H, Cullen N J, et al. Reconstructing the mass balance of Brewster Glacier, New Zealand, using MODIS-derived glacier-wide albedo[J]. The Cryosphere, 2016, 10(5): 2465-2484. DOI:10.5194/tc-10-2465-2016 |
| [2] |
Hock R. Glacier melt:a review of processes and their modelling[J]. Progress in Physical Geography, 2005, 29(3): 362-391. DOI:10.1191/0309133305pp453ra |
| [3] |
Hock R. Temperature index melt modelling in mountain areas[J]. Journal of Hydrology, 2003, 282(1-4): 104-115. DOI:10.1016/S0022-1694(03)00257-9 |
| [4] |
Cui Y H, Ye B S, Wang J, et al. Analysis of the spatial-temporal variations of the positive degree-day factors on the Glacier No.1 at the headwaters of the Urumqi river[J]. Journal of Glaciology and Geocryology, 2010, 32(2): 265-274. |
| [5] |
Schreider S Y, Whetton P H, Jakeman A J, et al. Runoff modelling for snow-affected catchments in the Australian alpine region, eastern Victoria[J]. Journal of Hydrology, 1997, 200(1): 1-23. |
| [6] |
Braithwaite R J, Olesen O B. Seasonal variation of ice ablation at the margin of the Greenland ice sheet and its sensitivity to climate change, Qamanârssûp sermia, West Greenland[J]. Journal of Glaciology, 1993, 39(132): 267-274. DOI:10.1017/S0022143000015938 |
| [7] |
Braithwaite R J. Positive degree-day factors for ablation on the Greenland ice sheet studied by energy-balance modelling[J]. Journal of Glaciology, 1995, 41(137): 153-160. DOI:10.1017/S0022143000017846 |
| [8] |
Braithwaite R J, Konzelmann T, Marty C, et al. Errors in daily ablation measurements in northern Greenland, 1993-94, and their implications for glacier climate studies[J]. Journal of Glaciology, 1998, 44(148): 583-588. DOI:10.1017/S0022143000002094 |
| [9] |
Liu Z, Yao Z, Huang H, et al. Land use and climate changes and their impacts on runoff in the Yarlung Zangbo River Basin, China[J]. Land Degradation & Development, 2014, 25(3): 203-215. |
| [10] |
Zhang Y, Liu S Y, Ding Y J. Observed degree-day factors and their spatial variation on glaciers in western China[J]. Annals of Glaciology, 2006, 43(1): 301-306. |
| [11] |
Ambach W. Interpretation of the positive-degree-days factor by heat balance characteristics-West Greenland[J]. Hydrology Research, 1988, 19(4): 217-224. DOI:10.2166/nh.1988.0014 |
| [12] |
You Q L, Kang S C, Yan Y P, et al. Climate change over the Yarlung Zangbo River Basin during 1961-2005[J]. Journal of Geographical Sciences, 2007, 17(4): 409-420. DOI:10.1007/s11442-007-0409-y |
| [13] |
Liu T S, Zhang X S, Xiong S F, et al. Glacial environments on the Tibetan Plateau and global cooling[J]. Quaternary International, 2002, 97(2): 133-139. |
| [14] |
Liu T C. Hydrological characteristics of Yalungzangbo river[J]. Acta Geographica Sinica, 1999, 54(S1): 157-164. |
| [15] |
Yao T D, Li Z G, Yang W, et al. Glacial distribution and mass balance in the Yarlung Zangbo River and its influence on lakes[J]. Chinese Science Bulletin, 2010, 55(20): 2072-2078. DOI:10.1007/s11434-010-3213-5 |
| [16] |
Qiao C J, He X B, Ye. B S. Study of the degree-day factors for snow and ice on the Dongkemadi glacier, Tanggula range[J]. Journal of Glaciology & Geocryology, 2010, 32(2): 257-264. |
| [17] |
Wu Q R, Kang S C, Gao T G, et al. The characteristics of the positive degree-day factors of the Zhadang glacier on the Nyainqêntanglha range of Tibetan plateau, and its application[J]. Journal of Glaciology & Geocryology, 2010, 32(5): 891-897. |
| [18] |
Bhakta K R, Ageta Y, Nakawo M. Positive degree-day factors for ablation on glaciers in the Nepalese Himalayas:Case study on glacier AX010 in Shorong Himal, Nepal[J]. Bulletin of Glaciological Research, 2000, 17: 1-10. |
| [19] |
Singh P, Kumar N, Arora M. Degree-day factors for snow and ice for Dokriani glacier, Garhwal Himalayas[J]. Journal of Hydrology, 2000, 235(1/2): 1-11. |
| [20] |
Braithwaite R, Zhang Y. Sensitivity of mass balance of five Swiss glaciers to temperature changes assessed by tuning a degree-day model[J]. Journal of Glaciology, 2000, 46(152): 7-14. DOI:10.3189/172756500781833511 |
| [21] |
Liu W G, Xiao C D, Liu J S, et al. Study of the degree factors on the Rongbuk glacier in the Mt. Qomolangma, Central Himalayas[J]. Journal of Glaciology and Geocryology, 2014, 36(5): 1101-1110. |
| [22] |
Zhang C W, Tang J K, Yu X J, et al. Quantitative retrieval of soil salt content based on remote sensing in the Yellow River delta[J]. Journal of Graduate University of Chinese Academy of Sciences, 2013, 30(2): 220-227. |
| [23] |
Wang P Y, Wei L S. Small sample properties of a kind of linear estimation in linear regression model[J]. Journal of Graduate School of Chinese Academy of Sciences, 2009, 26(3): 296-302. |
| [24] |
Jennrich, Sampson P F. Application of stepwise regression to non-linear estimation[J]. Technometrics, 1968, 10(1): 63-72. DOI:10.1080/00401706.1968.10490535 |
| [25] |
Rakshit S, Ghosh A, Shankar B U. Fast mean filtering technique (FMFT)[J]. Pattern Recognition, 2007, 40(3): 890-897. DOI:10.1016/j.patcog.2006.02.008 |
| [26] |
Jones J A A. Climate change and sustainable water resources:placing the threat of global warming in perspective[J]. Hydrological Sciences Journal, 1999, 44(4): 541-557. DOI:10.1080/02626669909492251 |
| [27] |
Zhu C D, Lu Y, Shi H L, et al. Spatial and temporal patterns of the inter-annual oscillations of glacier mass over Central Asia inferred from gravity recovery and climate experiment (GRACE) data[J]. Journal of Arid Land, 2017, 9(1): 87-97. DOI:10.1007/s40333-016-0021-z |
| [28] |
Yi S, Sun W K. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models[J]. Journal of Geophysical Research:Solid Earth, 2014, 119(3): 2504-2517. DOI:10.1002/2013JB010860 |
| [29] |
Che T, Li X, Jin R, et al. Snow depth derived from passive microwave remote-sensing data in China[J]. Annals of Glaciology, 2008, 49(1): 145-154. |
 2018, Vol. 35
2018, Vol. 35 


