随着移动通信技术的迅猛发展，智能终端的快速普及，移动数据容量需求正以惊人的速度增加。毫米波由于具备大量未经使用的频段，被视为第五代移动通信系统中解决容量需求的关键技术之一^[1]。毫米波由于波长较短，基站端可以以较小的物理阵列尺寸配置较多的天线。在传统的纯数字基带预编码方案中，每根天线都有对应的基带和射频链路结构，这些射频链路不仅造价昂贵而且功耗较大，在配置较多天线的毫米波通信系统中采用这种预编码方案是不切实际的。为解决上述问题，学术界提出在毫米波MIMO系统中采用混合数/模预编码结构^[2]。混合数/模预编码在发射端将数据流经基带数字预编码处理后映射到各个射频链路上，然后通过恒模相移器调整各个射频链路上信号的相位完成模拟预编码。在此结构上，射频链路的数目远远小于天线的数目，从而降低通信系统对硬件的需求，同时也没有对系统的性能造成明显的损失^[3-4]。

近年来，由于能源短缺以及温室效应的影响，通信系统的能耗问题也受到广泛关注。能量效率作为权衡系统容量和系统能耗的性能指标，成为未来无线通信研究的热点之一^[5]。目前，有大量文献对微波MIMO系统下能效优化问题进行了广泛研究，如Pa Tervo等^[6]在多用户MISO场景下提出一种能效最优的波束成形方案；Shi等^[7]在干扰广播信道下设计一种优化能效的迭代算法。

然而毫米波通信系统下新型混合预编码结构的提出为能效优化问题带来了更多新的难点：1)模拟预编码器的恒模限制为原目标问题带来了非凸的限制；2)射频链路数对系统能效有很大影响^[8]，但是由于其数值与模拟预编码矩阵和数字预编码矩阵的维度直接相关，难以通过数值分析得到其最优解.虽然目前已有少部分文献关注毫米波混合预编码系统下的能效优化问题，如文献[9]在给定射频链路数目的条件下通过将毫米波混合预编码的能效优化问题转化为求解欧式距离最小的问题，利用正交匹配追踪算法得出原问题的近似最优值；文献[10]同样利用正交匹配追踪法，在遍历每个可能的射频链路数目后，获得系统能效的最优值。然而上述文献都忽略了难点2)，而使用预先设定好的射频链路数目，从而降低了求解难度。这样做一方面忽略了射频链路数对系统能效的影响；另一方面当天线数目较多的时候，穷举搜索每个可能的射频链路数目将会十分耗时。

基于上述研究现状，本文在多用户毫米波MIMO系统下，提出一种基于射频链路选择的能效优化算法。由于原问题难以直接求解，首先引入一个预设的模拟预编码码本将问题等价转换为求解稀疏数字预编码^[11-12]，而模拟预编码则为从码本中选择出来的N_RF个码字，其中N_RF为最优的射频链路数目；接着由于转化后的问题仍然为一个非凸非线性问题，我们利用顺序凸近似理论结合Dinkelbach’s理论将问题变为凸问题并进行迭代求解。仿真结果表明，所提算法性能十分接近于穷举法性能，并且远远高于等增益传输(EGT)算法^[13]性能。

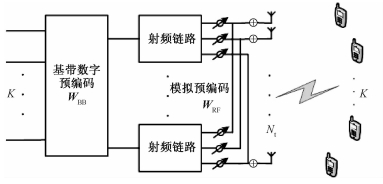
1 系统模型 1.1 信道模型

考虑毫米波单小区下行链路场景，如图 1所示。该系统由K个单天线用户和一个配置N_t根天线的基站组成。基站端射频链路的数目为N_RF，其取值范围为[K, N_t]。基站采用全连接的混合数\模预编码结构，包含一个N_RF×K的基带数字预编码器W_BB和一个N_t×N_RF的由恒模移相器构成的模拟预编码器W_RF。第k个用户接收到的信号可以表示为

$ {y_k} = \mathit{\boldsymbol{h}}_k^{\rm{H}}{\mathit{\boldsymbol{W}}_{{\rm{RF}}}}{\mathit{\boldsymbol{W}}_{{\rm{BB}}}}\mathit{\boldsymbol{s}} + {n_k}. $

(1)

式中：s=[s₁, s₂, …, s_K]^T；s_k~CN(0, 1)代表传输给第k个用户的信号；n~CN(0, σ²I_K)是独立同分布的加性高斯白噪声，其均值为0，方差为σ²；基站到K个用户的信道为H=[h₁, h₂, …, h_K]^H，其中h_k表示从基站到第k个用户的下行信道.本文采用基于角度扩展的Saleh-Valenzuela模型刻画毫米波信道^[3]，其目前被广泛应用于毫米波混合预编码的研究。h_k可以表示为

$ {\mathit{\boldsymbol{h}}_k} = \sqrt {\frac{{{N_{\rm{t}}}{\rho _k}}}{{{N_{{\rm{ray}}}}}}} \sum\limits_{i = 1}^{{N_{{\rm{ray}}}}} {{\alpha _{ki}}\mathit{\boldsymbol{u}}\left( {{\varphi _i},{\theta _i}} \right)} . $

(2)

式中：N_ray是从基站到K个用户的多径数目；ρ_k=ξ/r_k^κ是大尺度衰减因子；ξ是服从正太分布的随机数，均值为0，方差为9.7 dB^[14]；r_k是基站与第k个用户之间的距离；κ是路径损耗指数；α_ki是基站到第k个用户的第i条传输路径的复增益；φ_i和θ_i分别是天线的到达方位角和仰角，并且服从范围在$\left[ {\frac{{ - \pi }}{2},\frac{\pi }{2}} \right]$的均匀分布；u(φ_i, θ_i)代表发射天线阵列响应矢量，如下式所示

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}\left( {{\varphi _i},{\theta _i}} \right) = \frac{1}{{\sqrt {{N_t}} }}\left[ {1, \cdots ,{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }d\left( {p\sin {\varphi _i}\sin {\theta _i} + q\cos {\theta _i}} \right)}}} \right.}\\ {\left. {, \cdots ,{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }d\left( {\left( {\sqrt {{N_t}} - 1} \right)\sin {\varphi _i}\sin {\theta _i} + \left( {\sqrt {{N_t}} - 1} \right)\cos {\theta _i}} \right)}}} \right].} \end{array} $

(3)

式中：λ是波长；天线元素间的间隔d是波长的一半；p和q分别是天线在2D平面的索引，本文采用方形阵列，因此有0≤p≤$\sqrt {{N_{\rm{t}}}} - 1$，0≤q≤$\sqrt {{N_{\rm{t}}}} - 1$。

1.2 能耗模型

由于在移动通信系统当中，基站端占主要的功率消耗，因此，本文不考虑用户的功率消耗。基站的总功率消耗通常包括信号传输功耗以及电路功耗，所以毫米波通信系统的一般功耗模型^[2]为

$ {P_{{\rm{total}}}} = \frac{1}{\varepsilon }{P_{\rm{t}}} + {N_{{\rm{RF}}}}{P_{{\rm{RF}}}} + {P_{\rm{c}}}. $

(4)

式中：功率放大器的系数ε＜1，为一个常数；P_t为发射功耗并且有P_t=‖W_RFW_BB‖_F²。为方便起见，把与发射功耗P_t无关的所有功耗记为电路功耗，其包括由射频链路造成的动态电路功耗N_RFP_RF，以及基站端与天线数目和射频链路数目无关的基本功率消耗P_c。P_RF是指射频器件的功耗，包括发射滤波器、混频器、频率合成器、AD/DA转换器在内的所有功耗之和。

2 基于射频链路选择的高能效混合预编码设计 2.1 问题形成

上述毫米波系统模型下的能效优化问题可以建模成如下形式：

$ \begin{array}{l} \mathop {\max }\limits_{{\mathit{\boldsymbol{W}}_{{\rm{RF}}}},{\mathit{\boldsymbol{W}}_{{\rm{BB}}}},{N_{{\rm{RF}}}}} \frac{{{R_{{\rm{sum}}}}}}{{{P_{{\rm{total}}}}}}\\ {\rm{s}}.\;{\rm{t}}.\;{\left| {{\mathit{\boldsymbol{W}}_{{\rm{RF}}}}\left( {i,j} \right)} \right|^2} = \frac{1}{{{N_{\rm{t}}}}}\\ \;\;\;\;\;{R_k} \ge {\gamma _k},\forall k = 1, \cdots ,K\\ \;\;\;\;\;\sum\limits_{k = 1}^K {{{\left\| {{\mathit{\boldsymbol{W}}_{{\rm{RF}}}}{\mathit{\boldsymbol{w}}_{{\rm{BB}},k}}} \right\|}^2}} \le {P_{\max }}\\ \;\;\;\;\;{N_{{\rm{RF}}}} \ge K. \end{array} $

(5)

式中：P_max是最大的发射功率；R_k是第k个用户的速率，可以表示为

$ {R_k} = {\log _2}\left( {1 + \frac{{{\mathit{\boldsymbol{h}}_k}{\mathit{\boldsymbol{W}}_{{\rm{RF}}}}{\mathit{\boldsymbol{w}}_{{\rm{BB}},k}}\mathit{\boldsymbol{w}}_{{\rm{BB}},k}^{\rm{H}}\mathit{\boldsymbol{W}}_{{\rm{RF}}}^{\rm{H}}\mathit{\boldsymbol{h}}_k^{\rm{H}}}}{{\sum\limits_{i = 1,i \ne k}^K {{\mathit{\boldsymbol{h}}_k}{\mathit{\boldsymbol{W}}_{{\rm{RF}}}}{\mathit{\boldsymbol{w}}_{{\rm{BB}},i}}\mathit{\boldsymbol{w}}_{{\rm{BB}},i}^{\rm{H}}\mathit{\boldsymbol{W}}_{{\rm{RF}}}^{\rm{H}}\mathit{\boldsymbol{h}}_k^{\rm{H}}} + {\sigma ^2}}}} \right). $

(6)

用户的和速率即为R_sum=$\sum\limits_{k = 1}^K {{R_k}} $；γ_k是用户k的最小速率需求，本文定义当每个用户的速率都满足这个最小速率需求时，系统的服务质量(QoS)得到了保证。模拟预编码器由恒模的移相器构成，因此模拟预编码矩阵中的每个元素均满足幅值为1的条件，即|W_RF(i, j)|²=$\frac{1}{{{N_{\rm{t}}}}}$。式(5)中，W_RF和W_BB的维度随射频链路数N_RF的变化而变化，并且射频链路数N_RF必须满足不小于用户数的条件。从式(5)可以看出，系统的能效，即$\frac{{{R_{{\rm{sum}}}}}}{{{P_{{\rm{total}}}}}}$是受预编码矩阵W_RF和W_BB共同影响的，而系统的最大发射功率限制P_max、系统的天线数目N_t、以及射频链路的数目N_RF都会对预编码矩阵W_RF和W_BB的幅值和维度造成影响。当P_max越大，每根天线上可发送的功率越多，预编码矩阵的幅值变大，因而用户和速率增加，但同时系统功耗也增加。因此在一定范围内系统能效是随着P_max的增加而变大，此时P_max对和速率的影响超过对系统能耗的影响，然而当P_max超出一定范围后，和速率提升有限，而能耗仍呈线性增加，此时系统的能效不会再增加而是应该维持不变。系统发射天线数目N_t以及射频链路数目N_RF则会改变预编码矩阵的维度，当这二者变大时，预编码矩阵的维度增加，相应的和速率变大而能耗也同时增加。本文将在第3节通过仿真进一步说明上述系统参数对系统能效的影响。

2.2 问题模型转换

为了最大化系统能效，需要同时优化式(5)中的3个变量：W_RF，W_BB以及N_RF。由于W_RF和W_BB的大小与N_RF直接相关，并且目标问题非凸非线性，式(5)变得十分复杂而难以直接求解。尽管文献[10]通过穷举法搜索每个可能的N_RF下的系统能效从而获得了最优值，但当天线数目较多时，这种方法耗时太多，复杂度太高。为避免穷举搜索并让问题变得可解，下面将对原问题作进一步转换，使原三元耦合变量优化问题变成一个只包含一元变量的稀疏数字预编码优化问题。

考虑模拟预编码矩阵W_RF是从一个预设的码本中选出的N_RF个码字组成的，这里用符号${\mathscr{W}_{{\rm{RF}}}}$表示该码本，并且该码本中的所有元素模值恒定为$1/\sqrt {{N_{\rm{t}}}} $。采用一个N_t×N_t大小的离散傅里叶变换(DFT)矩阵^[15]表示该码本，这样做的原因在于：1)DFT矩阵中的每个列向量是不相关的；2)DFT矩阵中的列向量可以通过线性组合来合成空间中任意方向上的阵列响应矢量。该N_t×N_t的DFT矩阵可以表示为

$ \frac{1}{{\sqrt {{N_{\rm{t}}}} }}{\left[ {1,{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{{{N_{\rm{t}}}}}\left( {k - 1} \right)}}, \cdots ,{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{{{N_{\rm{t}}}}}\left( {k - 1} \right)\left( {{N_t} - 1} \right)}}} \right]^{\rm{T}}},k = 1,2, \cdots ,{N_{\rm{t}}}. $

(7)

每一列表示码本${\mathscr{W}_{{\rm{RF}}}}$中的一个码字.

因此，模拟预编码的设计可以看成是从码本${\mathscr{W}_{{\rm{RF}}}}$中挑选合适的码字。令${\mathit{\boldsymbol{\tilde W}}_{{\rm{RF}}}}$=${\mathscr{W}_{{\rm{RF}}}}$Q为W_RF的稀疏形式，它表示从码本${\mathscr{W}_{{\rm{RF}}}}$中挑选出N_RF个码字，并用N_t-N_RF个全零列向量进行填充后的矩阵，其大小为N_t×N_t。Q为一个对角矩阵，对角线上的元素是一个二值0-1变量，当对角线上的元素为1时表示该下标所对应的码本中的列向量被选中。令${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$为一个N_t×K的矩阵，它包含N_t-N_RF个全零行和W_BB的全部元素，${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$为W_BB的稀疏表示，并且满足${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$的全零行索引对应${\mathit{\boldsymbol{\tilde W}}_{{\rm{RF}}}}$全零列索引。综上，有如下等式成立：

$ {\mathit{\boldsymbol{W}}_{{\rm{RF}}}}{\mathit{\boldsymbol{W}}_{{\rm{BB}}}} = {{\mathit{\boldsymbol{\tilde W}}}_{{\rm{RF}}}}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{BB}}}} = {\mathscr{W}_{{\rm{RF}}}}\mathit{\boldsymbol{Q}}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{BB}}}} = {\mathscr{W}_{{\rm{RF}}}}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{BB}}}}. $

(8)

其中N_RF等于${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$的非零行的个数.

利用等式(8)，式(5)可以等价转化为

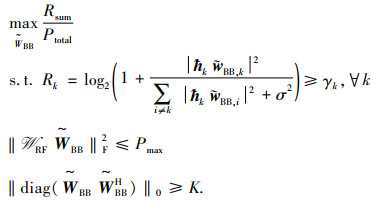
(9)

式中系统的总功耗为${P_{{\rm{total}}}} = \frac{1}{\varepsilon }\left\| {{{\mathscr{W}}_{{\rm{RF}}}}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{BB}}}}} \right\|_{\rm{F}}^2 + {\left\| {{\rm{diag}}\left( {{{\tilde W}_{{\rm{BB}}}}\;\;\tilde W_{{\rm{BB}}}^{\rm{H}}} \right)} \right\|_0}{P_{{\rm{RF}}}} + {P_{\rm{c}}}$，${\mathit{\boldsymbol{\tilde w}}_{{\rm{BB, }}k}}$是${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$的第k个列向量，而=h_kW_RF, ∀k，是第k个用户的等效信道。

通过上述转换, 式(9)只包含一个未知变量，即稀疏的数字预编码矩阵${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$。原问题即可看成是一个求解稀疏数字预编码矩阵与码字选择的过程。码本${\mathscr{W}_{{\rm{RF}}}}$中的每个码字可以被看成是一个虚拟的发射天线，其到第k个用户的虚拟信道即为。当${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$的第i行为全零行，表明${\mathscr{W}_{{\rm{RF}}}}$的第i个码字没有被选中。

2.3 算法设计

式(9)中的问题是一个经典的分式规划问题，利用Dinkelbach’s理论^[16-17]，通过引入参数η，将分式规划问题转化为等效的线性规划问题，从而最优单一预编码矩阵可以通过求解J(η)=0而得到。其中J(η)为

$ J\left( \eta \right) = \mathop {\max }\limits_{{{\tilde W}_{{\rm{BB}}}}} \sum\limits_{k = 1}^K {{R_k}} - \eta {P_{{\rm{total}}}}. $

(10)

该等价关系的含义是，如果可以找到一个最优值η^opt，使得J(η)=0成立，则其对应的最优解$\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}^{{\rm{opt}}}$就是优化问题(9)的最优解。本文采用经典的二分搜索法求解J(η)=0^[16]。可以看出，本文优化问题求解的关键步骤仍然是在给定η下，求解对应最优解$\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}^{{\rm{opt}}}$。所以，接下来本节将讨论给定η下子问题的求解方法。

首先，由于DFT矩阵是一个酉矩阵，因此有$\mathscr{W}_{{\rm{RF}}}^{{\rm{H}} \cdot }\mathscr{W}_{{\rm{RF}}}^ \cdot $=I_Nt。根据这个等式，总功率消耗可以写为${P_{{\rm{total}}}} = \frac{1}{\varepsilon }\left\| {{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{BB}}}}} \right\|_{\rm{F}}^2 + {\left\| {{\rm{diag}}\left( {{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{BB}}}}\;\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}^{\rm{H}}} \right)} \right\|_0}{P_{{\rm{RF}}}} + {P_c}$，式(9)中第2个约束条件也转变为‖W_RF ${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$‖_F²=‖${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$‖_F²≤P_max。

接下来，引入几个辅助变量，结合式(10)与式(9)中的约束条件, 子问题可以重写成如下形式：

(11)

显然，式(11)中所有的约束条件都取等号时达到最优，所以式(11)是原子问题的等价转换形式。问题(11)的求解难点在于其存在的的非凸约束 ${\mathit{\boldsymbol{\tilde w}}_{{\rm{BB, }}k}} \ge \sqrt {{\beta _k}{z_k}} $和零范数‖diag(${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$ $\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}^{\rm{H}}$)‖₀。

对于非凸约束 ${\mathit{\boldsymbol{\tilde w}}_{{\rm{BB, }}k}} \ge \sqrt {{\beta _k}{z_k}} $，采用顺序凸近似^[18]对它进行近似转换。文献[18]表明$\sqrt {{\beta _k}{z_k}} $可以用它的凸上界代替并在求解过程中对其中的参数进行迭代的更新。具体来说，定义G(ϕ_k, β_k, z_k)=$\frac{{{\phi _k}}}{2}z_k^2 + \frac{1}{{2{\phi _k}}}{\beta _k}$，对于一个固定的ϕ_k，ϕ_k＞0，有G(ϕ_k, β_k, z_k)≥$\sqrt {{\beta _k}} {z_k}$。因此 ${\mathit{\boldsymbol{\tilde w}}_{{\rm{BB}}, k}} \ge \sqrt {{\beta _k}} {z_k}$可以被转换为 ${{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}}, k}} \ge G\left( {{\phi _k}, {\beta _k}, {z_k}} \right)$，在每次迭代中，对于一个固定的ϕ_k， ${{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}}, k}} \ge G\left( {{\phi _k}, {\beta _k}, {z_k}} \right)$都是一个凸约束。

其次，考虑‖diag(${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$ $\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}^{\rm{H}}$)‖₀的l₀范数问题。引入选择变量x_i∈{0, 1}，它表示第i个码字是否被选中，1代表被选中，0代表未被选中。显然，当第i个码字未被选中时，对所有用户，${{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}}, k}}$的第i个元素皆为0，即${x_i} = 0 \Rightarrow {{\mathit{\boldsymbol{\bar w}}}_i} = 0, {{\mathit{\boldsymbol{\bar w}}}_i} \buildrel \Delta \over = {\left[ {{{\left[ {{\mathit{\boldsymbol{w}}_1}} \right]}_i}, {{\left[ {{\mathit{\boldsymbol{w}}_2}} \right]}_i}, \cdots , {{\left[ {{\mathit{\boldsymbol{w}}_K}} \right]}_i}} \right]^{\rm{T}}} \in {\mathbb{C}^{K \times 1}}$是${\mathit{\boldsymbol{\tilde W}}_{{\rm{BB}}}}$的第i个行向量。上述过程转化为约束形式，可以写成$\left\| {{{\mathit{\boldsymbol{\bar w}}}_i}} \right\|_2^2 < {f_i}{x_i}$，其中f_i被视为每个码字对应的功率水平。当x_i被松弛为一个0到1之间的连续变量时，$\left\| {{{\mathit{\boldsymbol{\bar w}}}_i}} \right\|_2^2 < {f_i}{x_i}$的二阶锥约束可以写成${\left\| {\mathit{\boldsymbol{\bar w}}_i^{\rm{T}}, \frac{1}{2}\left( {{f_i} - {x_i}} \right)} \right\|^2} < \frac{1}{2}\left( {{f_i} + {x_i}} \right)$。

综合上述所有结果，给定η下的子问题(11)的求解被转化为一个凸问题，问题的数学描述如式(12)所示

$ \begin{array}{l} \max \tau \\ {\rm{s}}.\;{\rm{t}}.\;\sum\limits_{k = 1}^K {{{\log }_2}\left( {{\beta _k} + 1} \right)} \ge \tau + \eta \left( {\frac{1}{\varepsilon }\sum\limits_{i = 1}^{{N_t}} {{f_i}} + \sum\limits_{i = 1}^{{N_t}} {{x_i}} \times {P_{{\rm{RF}}}} + {P_{\rm{c}}}} \right)\\ \;\;\;\;{\left\| {\mathit{\boldsymbol{\bar w}}_i^{\rm{T}},\frac{1}{2}\left( {{f_i} - {x_i}} \right)} \right\|^2} < \frac{1}{2}\left( {{f_i} + {x_i}} \right)\\ \;\;\;\;{{\mathit{\boldsymbol{\tilde h}}}_k}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{BB}},k}} \ge \frac{{{\phi _k}}}{2}z_k^2 + \frac{1}{{2{\phi _k}}}{\beta _k},\forall k\\ \;\;\;\;\sum\limits_{i = 1}^{{N_t}} {{f_i}} \le {P_{\max }};0 \le {x_i} \le 1,\forall i;\sum\limits_{i = 1}^{{N_t}} {{x_i}} \ge K\\ \;\;\;\;{z_k} \ge {\left( {{\sigma ^2} + \sum\limits_{i \ne k}^K {{{\left\| {{{\mathit{\boldsymbol{\tilde h}}}_k}{{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}},i}}} \right\|}^2}} } \right)^{1/2}}\\ \;\;\;\;\frac{1}{{\sqrt {{{\bar \gamma }_k}} }}{{\mathit{\boldsymbol{\tilde h}}}_k}{{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}},k}} \ge {\left( {{\sigma ^2} + \sum\limits_{i \ne k}^K {{{\left\| {{{\mathit{\boldsymbol{\tilde h}}}_k}{{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}},i}}} \right\|}^2}} } \right)^{1/2}}\\ \;\;\;\;{\mathop{\rm Im}\nolimits} \left( {{{\mathit{\boldsymbol{\tilde h}}}_k}{{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}},k}}} \right) = 0. \end{array} $

(12)

整个问题的算法求解步骤如表 1所示，它包括两个嵌套循环，外层二分查找η使J(η)=0，内层在固定η的条件下，求解式(12)对应的能效最优值。

在式(12)中，由于x_i被松弛为一个[0, 1]上的连续变量，采用一个简单的匹配原则：对于x_i＞1-ζ，令x_i=1；否则，令x_i=0。这里ζ是一个十分小的数。下节的仿真结果中表明，这种匹配算法对性能的影响几乎可以忽略不计，这是因为求解得到的x_i大部分都十分接近于1或者0。通过匹配后的x_i，可以找到码本中被选择的码字，从而组成模拟预编码矩阵W_RF。用${\mathit{\boldsymbol{\tilde h}}_k}$=h_kW_RF以及${P_{{\rm{total}}}} = \frac{1}{\varepsilon }\left\| {{\mathit{\boldsymbol{W}}_{{\rm{RF}}}}\;{\mathit{\boldsymbol{W}}_{{\rm{BB}}}}} \right\|_{\rm{F}}^2 + \sum\limits_{k = 1}^K {{x_i}{P_{{\rm{RF}}}} + {P_{\rm{c}}}} $来代入新式(12)，再次重复算法1中的步骤，求解出数字预编码矩阵W_BB，得到系统能效的最优值。

3 仿真结果与分析

本节将对上述算法进行仿真性能验证，仿真中所用部分参数^[2-10]如表 2所示。在不作特殊说明的情况下，用户数K=4，发射天线数N_t=64，最大发射功率P_max=30 dBm。

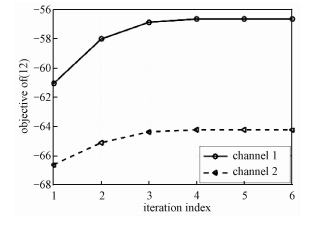
图 2验证了算法1内层循环的收敛性，容错误差设置为gap=10^-6。经观察发现，内层循环在几个迭代后就可以收敛至局部最优点。这是因为，在非凸约束条件 ${{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}}, k}} \ge \sqrt {{\beta _k}} {z_k}$中，本文用$\sqrt {{\beta _k}} {z_k}$的凸上界G(ϕ_k, β_k, z_k)=$\frac{{{\phi _k}}}{2}z_k^2 + \frac{1}{{2{\phi _k}}}{\beta _k}$进行替代，在每次迭代中，对于一个固定的ϕ_k， ${{\mathit{\boldsymbol{\tilde w}}}_{{\rm{BB}}, k}} \ge G\left( {{\phi _k}, {\beta _k}, {z_k}} \right)$都是一个凸约束。假设在第n+1次迭代中，用(β_k⁽ⁿ⁾, z_k⁽ⁿ⁾)代替(β_k, z_k)，用W⁽ⁿ⁾代替W，那么问题(12)中的约束条件仍然可以满足，也就是说第n次迭代产生的最优值是第n+1次迭代的一个可行点。那么第n+1次迭代结果总是不小于第n次迭代结果，因而多次迭代产生的是一列非递减的值。而问题(12)又受到总功率的约束，因此算法的内层循环最后可以收敛到一个局部最优点。而算法1的外层循环通过二分法可以保证收敛，因此整个算法1的收敛性可以得到保证。

为验证算法的有效性，从多个角度对所提算法进行比较。为评估算法1中x_i映射为0或1对系统造成的性能损失，将x_i映射前采用算法1(记为RFEE-Relax)得到的结果与x_i映射后再次采用算法1得到的结果(记为RFEE-Mapping)进行比较。为评估算法1射频链路选择对系统能效的优化，将所提RFEE-Mapping算法与穷举法以及EGT^{[13, 15]}算法进行对比。在EGT算法中，射频链路的数目必须与用户数目保持一致，模拟预编码矩阵W_RF中元素值为$\frac{1}{{\sqrt {{N_{\rm{t}}}} }}{{\rm{e}}^{{\rm{j}}\vartheta \left( {i, j} \right)}}$, ∀i, j，其中ϑ(i, j)是信道矩阵H第(i, j)个元素共轭转置后的相角。

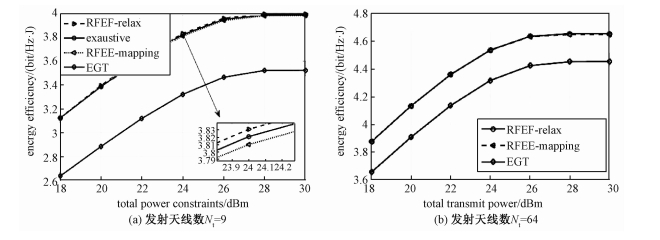
图 3比较几种算法的能效随最大传输功率P_max的变化情况.从仿真结果可以看出，对于每种算法，系统的能效都是随着P_max的增加，先增加后持平。比较RFEE-Relax算法以及RFEE-Mapping算法，可以看出，RFEE-Relax算法只略微优于RFEE-Mapping算法，这是因为RFEE-Relax算法得到的x_i值大部分都十分接近于0、1，所以x_i采用简单匹配规则对性能造成的损失几乎可以忽略不计。图 3(a)中，在较小发射天线数的情况下，对比采用穷举法得到最优射频链路数下的系统能效与采用RFEE-Mapping算法得到系统能效的性能差别。可以很直观地看出，所提RFEE-Mapping算法只稍逊于穷举法。而在图 3(b)中，由于天线数目增多，如果采用穷举法，需要重复进行$\left( \begin{array}{l} {N_{\rm{t}}}\\ K \end{array} \right) + \left( \begin{array}{l} {N_{\rm{t}}}\\ K + 1 \end{array} \right) + \cdots + \left( \begin{array}{l} {N_{\rm{t}}}\\ {N_{\rm{t}}} \end{array} \right)$种可能的混合预编码组合，这几乎是不可实现的。我们还对比了EGT算法与所提RFEE-Mapping算法的能效性能，可以看出，RFEE-Mapping算法大大优于EGT算法。这是因为，射频链路数目在一定范围内的增多使系统频效的增加高于系统能耗，从而提高了系统的能效。

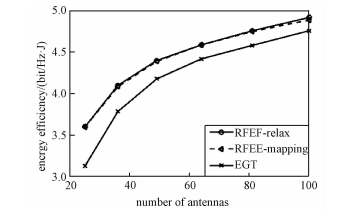
图 4展示不同发射天线数目对系统能效造成的影响。由于本文采用的天线阵列是方阵，因此图 4的横坐标取整数的平方。由仿真结果可以看出，天线数目越多，系统能效越高，但是随着天线数目的增加，系统能效增加速度趋于缓慢，并且RFEE-Mapping算法与EGT算法的性能差异也逐渐变小.这是因为虽然增加天线数目可以增加系统的频效但是也会额外增加系统的功耗，当天线数目大到一定程度的时候，天线数对频效的影响趋小而对能耗的影响趋大，从而使得能效增加趋于缓慢。

4 结束语

在毫米波混合预编码结构下，系统能效与射频链路数目的优化问题十分具有挑战性。本文提出一种基于射频链路选择的高能效混合预编码算法.首先利用预设的模拟预编码码本，将原问题等价转换为稀疏数字预编码优化问题，使得原问题的3个耦合变量转化为1个未知变量。随后利用Dinkelbach’s理论结合顺序凸近似设计一种迭代求解算法。结果显示，本文提出的算法可以在避免穷举搜索的情况下优化射频链路数目、有效提升系统能效，其结果与穷举法所获性能十分逼近，并显著高于其他常用算法。