2. 杰奥世博(北京)技术有限公司, 北京 100102
2. GeoCyber Solutions Inc., Beijing 100102, China
动校正是地震数据处理中的基本内容之一,也是水平叠加的基础。它关系到地震资料处理结果的精度和应用效果。经过动校正处理的地震数据才能实现叠加,达到提高信噪比、改善地震记录质量的目的,但在动校正过程中不可避免地要出现拉伸畸变,即信号时间拉长、频率向低频移动和波形变异现象,拉伸畸变严重时,不仅破坏叠加效果,也会使地震信号失去应有的波动力学特征,降低分辨率,从而影响地震勘探精度和地质效果[1]。
对于动校正拉伸现象,Buchholtz[2]定性地描述动校正的拉伸效应。Dunkin和Levin[3]在频率域研究拉伸效应,并认为动校正会使振幅谱发生改变。此后,大量研究者开始研究无拉伸的动校正方法。在国外,Rupert和Chun[4]提出BMS(block-move-sum)方法,用于减少动校正拉伸;Shatilo和Aminzadeh[5]提出CNMO(constant normal-moveout)改进了BMS方法。紧接着,Perroud和Tygel[6]也用BMS的思想对高分辨率的地震数据做无拉伸动校正。此外,Masoomzadeh等[7]和Zhang等[8]也分别对无拉伸动校正做出贡献。其中Zhang等[8]利用匹配追踪分解子波的技术实现无拉伸的动校正,Yang等[9]对此方法做了改进。Biondi等[10]通过迭代部分动校正与反褶积的方式消除拉伸,每次迭代过程中采用的是常规动校正方法,动校正结果仍然会引入拉伸畸变。Abedi和Riahi[11]则采用非双曲无拉伸动校正方法。在国内,赵波和史政军[12]通过寻找滤波用于消除校正后的拉伸;夏洪瑞等[13]通过计算动校正拉伸因子,进行反拉伸校正;尤建军和常旭[14]提出长偏移距地震数据非双曲无拉伸动校正方法;崔宝文和王维红[15]提出频谱代换无拉伸动校正方法;黄文锋等[16]和施剑等[17]将此方法应用于具体地震数据处理中,并取得一定效果;随后陈鑫等[18]介绍基于匹配追踪算法的非拉伸速度无关动校正;孙成禹等[19]通过在一定时窗内的互相关量,求出动校正修正量,帮助消除拉伸畸变。
本文提出的多子波动校正方法,是基于移动整个子波的思想,使子波在动校正时,不再发生子波拉伸畸变。本文首先回顾传统动校正的实现过程和地震道的多子波分解技术,其次根据动校正的理论,移动整个子波实现动校正处理。此方法的特点是自然地避免子波拉伸畸变现象,保留地震资料高频信息,提高地震资料的时间分辨率,同时容易实现,过程简单。
1 多子波动校正 1.1 传统动校正方法非零偏移距与零偏移距的双程旅行时的差,称为正常时差,记为ΔtNMO。Dix[20]的双曲近似旅行时方程广泛被应用于计算偏移距函数的旅行时t,如下:
| $ {t^2} = t_0^2 + \frac{{{x^2}}}{{{v^2}}}, $ | (1) |
式中:x为震源和检波器之间的距离(即炮检距或偏移距);v为反射面以上介质的速度;t0为零偏移距的双程旅行时。于是正常时差ΔtNMO为
| $ \Delta {t_{{\rm{NMO}}}} = t - {t_0}, $ | (2) |
把(2)式代入(1)式,有
| $ \Delta {t_{{\rm{NMO}}}} = {t_0}\left( {\sqrt {1 + {{\left( {\frac{x}{{v{t_0}}}} \right)}^2}} - 1} \right), $ | (3) |
正常时差ΔtNMO即为偏移距为x的地震道的动校正量。这种传统的动校正方法,以样点为基本单元,对于地震道中不同的样点t0值,会得到不同的校正量ΔtNMO。文献[13]详细推导了拉伸因子
根据理想的褶积模型,一个地震道s(t)可以表示为子波w(t)与反射系数r(t)的褶积,即
| $ s\left( t \right) = w\left( t \right) * r\left( t \right), $ | (4) |
而实际情况是地震子波在传播过程中,受不同传播路径,以及不同岩层物理特性的影响,子波的形状或频谱特征会发生不同的改变。多子波地震道模型[21]为更精确地表述地震道提供了一个新的基础,即
| $ s\left( t \right) = \sum\limits_{k = 1}^K {{w_k}\left( t \right) * r\left( {{t_k}} \right), } $ | (5) |
式中:wk(t)(k=1, 2, …, K)代表一个子波序列,序列中的子波可以具有不同的形状或频谱特征;rk(t)(k=1, 2, …, K)是对应同一子波的反射系数序列函数。当所有子波形状相同时,即w(t)=wk(t)(k=1, 2, …, K),有r(t)=
多子波分解技术[21-22]源于基追踪原理[23],地震道s可以用一个线性优化系统来表示,如下:
| $ \begin{array}{l} \min \;z = {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{x}}\\ \;{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\mathit{\boldsymbol{Ax}}{\rm{ = }}\mathit{\boldsymbol{s}}\\ \;\;\;\;\;\;\mathit{\boldsymbol{x}} \ge {\bf{0}}, \end{array} $ | (6) |
式中:目标函数z=cTx中c是单位列向量;x∈Rn;而矩阵A则是由子波库中的子波wk(t)生成的,具体如何构造矩阵A,可参考文献[22]。值得注意的是,在处理实际数据时,可以通过提取数据中的子波或者经验子波生成子波库[22]。线性优化系统(6)已经有很成熟的求解方法了,可以参考文献[26-28]。通过求解式(6),可得到
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{Wr}}, $ | (7) |
即式(7)为式(5)的矩阵形式。其中矩阵W的每一列为一个子波,向量r为该子波对应的反射系数。这就是多子波分解技术。因此,在多子波模型的基础上,利用多子波分解技术[21],地震道s(t)可以精确地表示为由不同振幅(由r(tk)确定),不同形状(由子波wk(t)确定),不同位置(由tk确定)的子波组成的集合。关于子波的选择,还可以参考文献[29-31]。Lin等[22]应用这一技术,提出基于移动子波的Kirchhoff叠前时间偏移技术,并在实际应用中取得良好效果。
1.3 多子波动校正多子波动校正,不以样点为处理单元,而以子波为处理单元,先用多子波分解技术,得到式(5),再根据传统的动校正理论,由式(3),对tk时刻的子波求得相对应的动校正量Δtk, NMO后,得到校正后的地震道
| $ {s_{{\rm{NMO}}}}\left( t \right) = \sum\limits_{k = 1}^K {{w_k}\left( t \right) * r\left( {{t_k} - \Delta {t_{k, {\rm{NMO}}}}} \right)} , $ | (8) |
由式(8)中,可以看出此多子波动校正方法,没有使子波wk(t)发生改变,也没有使子波振幅,即反射系数r(tk)的大小发生改变,具有保幅特性;而仅仅是改变了反射系数的时间,即由tk变为tk-Δtk, NMO,这就保证同一子波内的不同样点都采用相同的动校正量,自然地避免了传统的动校正会发生的子波拉伸畸变现象,不必再做拉伸切除处理,从而能保留更多的地震资料信息,有助于提高时间上的分辨率。
2 处理效果分析本文先采用两个理论模型对所提出的基于多子波的动校正的方法进行验证,第一个是小偏移距的多层水平模型,其CMP道集的反射同相轴不相交;第二个是同相轴存在相交的双反射层模型。然后进一步用实际数据资料验证多子波动校正的实用性。
在合成地震数据时可以选取任意子波,即不同频率、不同相位或者不同形状的子波,只要多子波分解时也用相同的子波即可。不失一般性,本文在合成地震图和多子波分解时均采用常用的Ricker子波[29],即
| $ {w_k}\left( t \right) = \left( {1 - 2{\pi ^2}f_k^2{t^2}} \right){{\rm{e}}^{ - {\pi ^2}f_k^2{t^2}}}, $ | (9) |
则子波形状由子波的主频fk决定。
2.1 无交叉的同相轴算例图 1(a)是利用褶积模型,合成的共中心点(CMP)道集,可以看出一共有5个水平反射层。在做多子波动校正之前,首先需要利用多子波分解技术,把这个CMP道集中的每一道都分解,即用多子波来表示,然后再做各子波的校正。图 1(b)与图 1(c)是多子波动校正与传统动校正的结果比较,可以看出多子波动校正,在校平同相轴的同时没有引起子波的拉伸,而传统动校正则在浅层远道端明显出现拉伸现象。

|
Download:
|
| 图 1 无交叉的同相轴动校正结果对比 Fig. 1 Comparison of the NMO results of non crossover event | |
图 2(a)是分别用主频为30和25 Hz的Ricker子波合成的CMP道集,虽只有两个反射层,但是它们之间存在交叉项。同样要对这个CMP道集做多子波分解,这时子波库只选择30和25 Hz的Ricker子波构成矩阵A,然后再做多子波动校正。图 2(b)与2(c)是多子波动校正与传统动校正的结果。可以看出,传统的动校正(图 2(c)),在不做任何切除的情况下,两个水平层虽然拉平了,但也保留了一些过校正与校正不足的事件[17],通常会把这些连同远端的地震道都一起切除,只保留近端的地震道。而多子波动校正(图 2(b))跟传统动校正一样都有一些过校正与校正不足的现象,但是可以看出没有发生子波拉伸现象,在远道端依然保持着几乎相同的频率,这些信息完全可以被保留下来,从而提高有效的叠加次数,进而提高地震资料的信噪比和分辨率。

|
Download:
|
| 图 2 交叉的同相轴动校正结果对比 Fig. 2 Comparison of the NMO results of crossover event | |
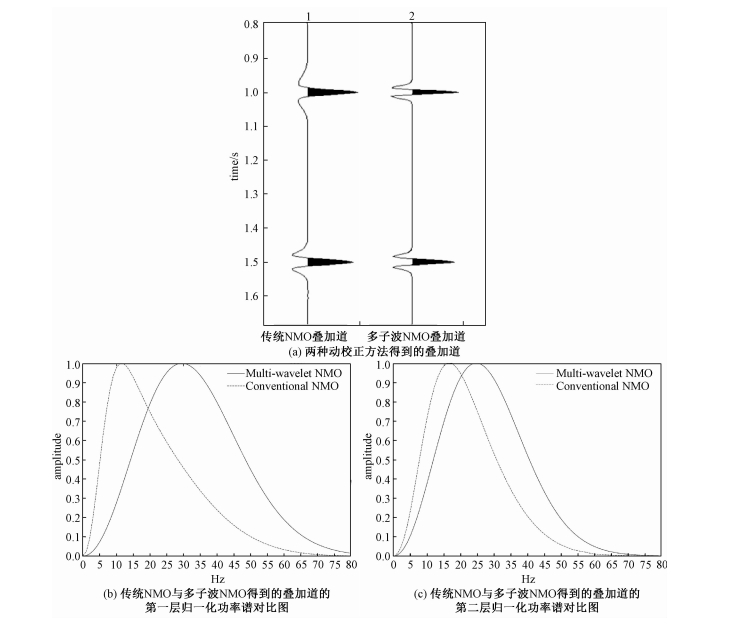
对这两种校正结果进行叠加,如图 3(a)所示,第1道为传统动校正后的结果,第2道为多子波校正后的结果。从图 3(a)中可以看出叠加结果有细微差别,分别对两个反射层做功率谱分析对比,图 3(b)与3(c)是传统动校正后叠加道与多子动校正后叠加道的归一化的功率谱对比图。从图中可以看出经传统动校正后叠加道的频率在向低频移动,尤其是浅层(第一层)特别明显,主频直接从30 Hz移到大约12 Hz,而多子波动校正叠加道则几乎没有向低频移动,保持了原有的频率,主频分别为30与25 Hz,有较高的时间分辨率。
|
Download:
|
| 图 3 传统与多子波NMO得到的叠加道对比 Fig. 3 Comparison between the stack traces obtained using conventional and multi-wavelet NMO algorithms | |
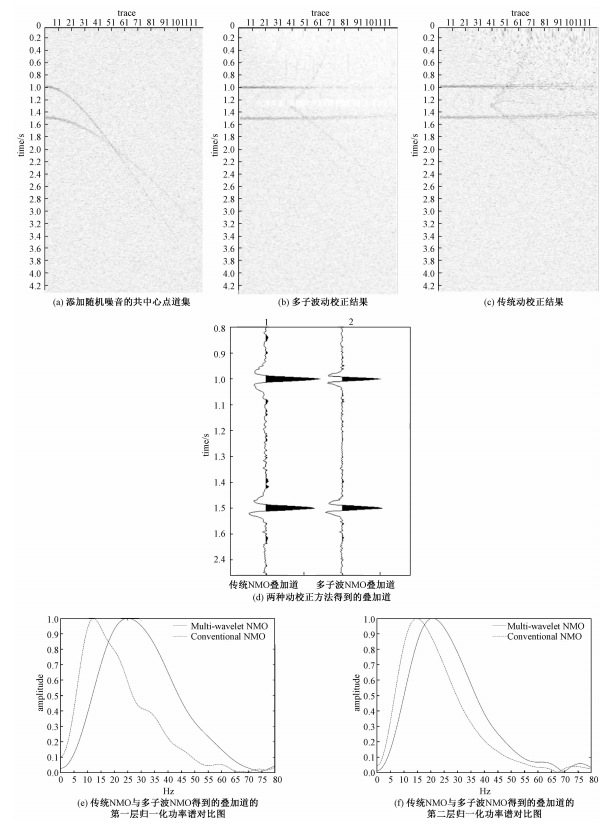
图 4是给模型数据添加随机噪音后,两种动校正结果的对比图。需要注意的是,加入随机噪音后,因子波受随机噪音的影响,就不能再用30与25 Hz的Ricker子波做子波库构造矩阵A了,这里选择1~120 Hz的Ricker子波来分解包含随机噪音的数据。从图 4(a)中可以看出,长偏移距的道,几乎看不出子波的形状了。图 4(b)与4(c)是多子波动校正与传统动校正的结果。从图 4(b)与4(c)的远端道,可以看出多子波动校正因噪声的干扰,少了那么一些同相轴。把它们叠加,如图 4(d)所示,同样得分别对两个反射事件做频谱分析对比,得到图 4(e)与4(f)。从中可以看出叠加以后传统动校正几乎保持一样的拉伸(与图 3(b)和3(c)比较),而多子波动校正在加入噪声后,频率也有所降低。说明常规动校正拉伸畸变对信噪比变化不敏感,多子波动校正对噪音较为敏感,因此,在使用多子波动校正时,最好进行去噪处理,突出子波的特征。
|
Download:
|
| 图 4 添加随机噪声后,动校正结果对比 Fig. 4 Comparison of the NMO results on a synthetic CMP gathering random noise | |
使用这样一个信噪比较高的实际数据,如图 5(a)所示,是其中一个CMP道集,在不知道该数据的子波的情况下,本文仍然采用1~120 Hz的Ricker子波分解该数据,然后做多子动校正。图 5(b)与5(c)分别是多子波动校正与传统动校正的结果,可以看到传统动校正的浅层拉伸较为严重,在叠加前需要人工切除。图 5(d)是多子波动校正没有经过切除处理而直接叠加的剖面,而图 5(e)则是传统动校正经过切除处理后的叠加剖面,可以看出传统动校正浅层是受到子波拉伸的影响,在进行叠加前的切除处理后,使叠加后频率受损,主频变低,这从图 5(f)的浅层(152~451 ms)平均振幅功率谱对比图,也可以更直观地看出多子波动校正在浅层不受拉伸切除的影响,有更高的分辨率。

|
Download:
|
| 图 5 实际数据动校正结果对比 Fig. 5 Comparison of the NMO results on the real data | |
本文提出的多子波动校正方法,以传统的动校正理论为基础,利用多子波分解技术分解地震数据,再以子波为处理单元,用整个子波进行校正,避免子波拉伸,从而避免切除处理,保留更多资料信息,提高时间分辨率。模型数据测试和实际资料处理验证了此方法的正确性与有效性。多子波动校正要求数据有较高的信噪比,需要做去噪处理;同时,多子波分解技术是多子波动校正的基础,而子波的提取又是多子波分解技术的关键。因此,提取有效子波[30],直接用多子波分解技术做去噪处理(类似于基追踪去噪(BPDN)[28]),以及提高多子波分解技术的运算速度,都将是进一步工作的研究内容。
| [1] |
何现启, 朱自强. 地震资料动校正拉伸畸变分析及处理方法[C]//中国地质学会, 中国金属学会. 当代矿山地质地球物理新进展. 三亚, 2004: 423-429. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDJ200400002081.htm
|
| [2] |
Buchholtz H. A note on signal distortion due to dynamic (NMO) corrections[J]. Geophysical Prospecting, 1972, 20(2): 395-402. DOI:10.1111/gpr.1972.20.issue-2 |
| [3] |
Dunkin J W, Levin F K. Effect of normal moveout on a seismic pulse[J]. Geophysics, 2012, 38(4): 635-642. |
| [4] |
Rupert G B, Chun J H. The block move sum normal moveout correction[J]. Geophysics, 1975, 40(1): 17-24. DOI:10.1190/1.1440511 |
| [5] |
Shatilo A, Aminzadeh F. Constant normal-moveout (CNMO) correction:a technique and test results[J]. Geophysical Prospecting, 2000, 48(3): 473-488. DOI:10.1046/j.1365-2478.2000.00190.x |
| [6] |
Perroud H, Tygel M. Nonstretch nmo[J]. Geophysics, 2004, 69(2): 599-607. DOI:10.1190/1.1707080 |
| [7] |
Masoomzadeh H, Barton P J, Singh S C. Nonstretch moveout correction of long-offset multichannel seismic data for subbasalt imaging:example from the North Atlantic[J]. Geophysics, 2010, 75(4): R83-R91. DOI:10.1190/1.3443579 |
| [8] |
Zhang B, Zhang K, Guo S, et al. Nonstretching NMO correction of prestack time-migrated gathers using a matching-pursuit algorithm[J]. Geophysics, 2013, 78(1): U9-U18. DOI:10.1190/geo2011-0509.1 |
| [9] |
Yang X, Cao S, Liu Q, et al. A modified nonstretching NMO correction using matching-pursuit algorithm[C]//SEG Technical Program Expanded Abstracts 2014. Society of Exploration Geophysicists, 2014: 517-521. https://www.researchgate.net/publication/269163019_A_modified_nonstretching_NMO_correction_using_matching-pursuit_algorithm
|
| [10] |
Biondi E, Stucchi E, Mazzotti A. Nonstretch normal moveout through iterative partial correction and deconvolution[J]. Geophysics, 2014, 79(4): V131-V141. DOI:10.1190/geo2013-0392.1 |
| [11] |
Abedi M M, Riahi M A. Nonhyperbolic stretch-free normal moveout correction[J]. Geophysics, 2016, 81(6): U87-U95. DOI:10.1190/geo2016-0078.1 |
| [12] |
赵波, 史政军. 消除动校正拉伸影响的方法[J]. 石油地球物理勘探, 1995, 30(3): 417-421. |
| [13] |
夏洪瑞, 葛川庆, 邹少峰. 动校拉伸现象分析及其消除[J]. 石油物探, 2005, 44(3): 220-224. DOI:10.3969/j.issn.1000-1441.2005.03.007 |
| [14] |
尤建军, 常旭. 长偏移距地震数据非双曲无拉伸动校正[C]//中国地球物理学会年会. 中国地球物理学会第二十一届年会论文集. 长春, 2005: 645. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDW200508001541.htm
|
| [15] |
崔宝文, 王维红. 频谱代换无拉伸动校正方法研究[J]. 地球物理学进展, 2007, 22(3): 960-965. DOI:10.3969/j.issn.1004-2903.2007.03.045 |
| [16] |
黄文锋, 李宏兵, 姚逢昌, 等. 子波拉伸校正[J]. 地球物理学进展, 2011, 26(5): 1642-1651. DOI:10.3969/j.issn.1004-2903.2011.05.017 |
| [17] |
施剑, 吴志强, 刘江平, 等. 动校正拉伸分析及处理方法[J]. 海洋地质与第四纪地质, 2011(4): 187-194. |
| [18] |
陈鑫, 王德利, 孟阁阁. 基于匹配追踪算法的非拉伸速度无关动校正[C]//中国地球物理学会, 中国地质学会. 2014年中国地球科学联合学术年会论文集. 北京, 2014: 1179. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDW201410024044.htm
|
| [19] |
孙成禹, 谢俊法, 闫月锋, 等. 一种无拉伸畸变的动校正方法[J]. 石油物探, 2016, 55(5): 664-673. DOI:10.3969/j.issn.1000-1441.2016.05.005 |
| [20] |
Dix C H. Seismic velocities from surface measurements[J]. Geophysics, 1955, 20(1): 68-86. DOI:10.1190/1.1438126 |
| [21] |
An P. Application of multi-wavelet seismic trace decomposition and reconstruction to seismic data interpretation and reservoir characterization[C]//SEG Technical Program Expanded Abstracts 2006. Society of Exploration Geophysicists, 2006: 973-977. http://www.researchgate.net/publication/242666273_Application_of_multi-wavelet_seismic_trace_decomposition_and_reconstruction_to_seismic_data_interpretation_and_reservoir_characterization
|
| [22] |
Lin L, Shi B, An P. Multiwavelet prestack Kirchhoff migration[J]. Geophysics, 2016, 81(3): S79-S85. DOI:10.1190/geo2015-0140.1 |
| [23] |
Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM review, 2001, 43(1): 129-159. DOI:10.1137/S003614450037906X |
| [24] |
Zhang R, Castagna J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
| [25] |
Zhang R, Sen M K, Srinivasan S. A prestack basis pursuit seismic inversion[J]. Geophysics, 2013, 78(1): R1-R11. |
| [26] |
Gondzio J. Interior point methods 25 years later[J]. European Journal of Operational Research, 2012, 218(3): 587-601. DOI:10.1016/j.ejor.2011.09.017 |
| [27] |
Gill P R, Wang A, Molnar A. The In-Crowd Algorithm for Fast Basis Pursuit Denoising[J]. IEEE Transactions on Signal Processing, 2011, 59(10): 4595-4605. DOI:10.1109/TSP.2011.2161292 |
| [28] |
Chen H, Cao S, Yuan S, et al. Nonstationary sparse deconvolution with the SPGL1 algorithm[C]//International Geophysical Conference, Qingdao, China, 17-20 April 2017. Society of Exploration Geophysicists and Chinese Petroleum Society, 2017: 194-197. https://www.researchgate.net/publication/317294545_Nonstationary_Sparse_Deconvolution_with_the_SPGL1_Algorithm
|
| [29] |
Ricker N. The form and laws of propagation of seismic wavelets[J]. Geophysics, 1953, 18(1): 10-40. DOI:10.1190/1.1437843 |
| [30] |
杨培杰, 印兴耀. 地震子波提取方法综述[J]. 石油地球物理勘探, 2008, 43(1): 123-130. DOI:10.3321/j.issn:1000-7210.2008.01.021 |
| [31] |
黄跃, 许多, 文雪康. 多子波分解与重构中子波的优选[J]. 石油物探, 2013, 52(1): 17-22. DOI:10.3969/j.issn.1000-1441.2013.01.003 |
 2018, Vol. 35
2018, Vol. 35 


