2. 中国科学院大学, 北京 100049;
3. 中国地质科学院地质研究所, 北京 100037;
4. 湖北省地震局, 武汉 430071
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Geology, Chinese Academy of Geological Sciences, Beijing 100037, China;
4. Earthquake Administration of Hubei Province, Wuhan 430071, China
分量式钻孔应变仪作为地应力监测的关键手段,记录地应变的长期变化,并为地应力的实时变化提供依据。钻孔应变仪可以记录高频的地震信息、以天时间尺度变化的固体潮信息、年周期变化和长年变化的信息[1-2],在构造应力场和地震预报研究中有着重要作用。钻孔应变仪还有观测一些对地震仪来说周期太长、对于GPS来说周期太小的慢地震的事件的潜力[3-4]。钻孔应变由于能够与GPS在不同时段和应变速率上互补,是一种对地壳运动和形变监测的主流仪器,提供连续的地壳形变数据[5]。
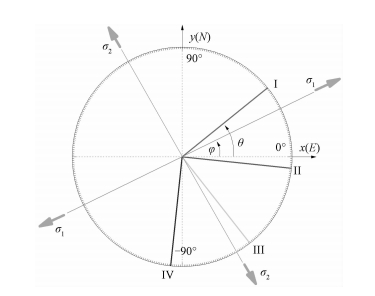
美国板块边界计划(Plate Boundary Observation, PBO)中,GTSM技术采用的是三分量的钻孔应变仪,3个元件依次间隔60°。中国采用的四分量钻孔应变仪,由4个依次间隔45°的元件组成。四分量,间隔45°的4个元件的钻孔应变元件布设方法1970年代由石耀霖提出[6-7],如图 1所示。四分量钻孔应变元件观测的提出最早是为了通过自检,从钻孔应变观测记录中排除非构造应力的影响[6]。
|
Download:
|
| 岩体内均匀应力场主应力为σ1、σ2,σ1与x轴的夹角为φ。元件Ⅰ与x轴的夹角为θ。元件Ⅱ、Ⅲ、Ⅳ夹角相继为45°。 图 1 中国四分量钻孔应变仪元件布设示意图(以姑咱台为例) Fig. 1 Layout of four-component borehole strain meter(Taking Guza borehole strain station as example) | |
钻孔元件读数Δεi(i=ⅠⅡⅢⅣ)情况下,若最大主应力方向与x轴夹角为ϕ,元件Ⅰ方向与x轴夹角为θ(均由x轴逆时针旋转为正),a为钻孔半径,则根据弹性力学理论,钻孔中Ⅰ元件在外应力场下径向位移如下所示:
| $ \Delta {\varepsilon ^{\rm{I}}} = A\left( {{\sigma _1} + {\sigma _2}} \right) + B\left( {{\sigma _1} - {\sigma _2}} \right)\cos 2\left( {\theta - \phi } \right), $ | (1) |
| $ \Delta {\varepsilon ^{{\rm{II}}}} = A\left( {{\sigma _1} + {\sigma _2}} \right) - B\left( {{\sigma _1} - {\sigma _2}} \right)\sin 2\left( {\theta - \phi } \right), $ | (2) |
| $ \Delta {\varepsilon ^{{\rm{III}}}} = A\left( {{\sigma _1} + {\sigma _2}} \right) - B\left( {{\sigma _1} - {\sigma _2}} \right)\cos 2\left( {\theta - \phi } \right), $ | (3) |
| $ \Delta {\varepsilon ^{{\rm{IV}}}} = A\left( {{\sigma _1} + {\sigma _2}} \right) + B\left( {{\sigma _1} - {\sigma _2}} \right)\sin 2\left( {\theta - \phi } \right). $ | (4) |
其中:ΔεⅠ=ΔurⅠ/a、ΔεⅡ=ΔurⅡ/a、ΔεⅢ=ΔurⅢ/a、ΔεⅣ=ΔurⅣ/a,分别为4路元件的读数。
对于岩体中有圆孔的简单情况,A=1/E,B=2/E,本文简化为仅考虑弹性岩体中的钻孔,对于考虑岩体和探头金属壁的两层,甚至考虑岩体、固定用的膨胀水泥、探头金属壁的更复杂的情况,A、B的表达式与各层的力学性质和厚度有关[8]。如果考虑水泥和套筒,A、B值变化约为11.9%,相差不大[9]。
可以从其中3个元件读数计算平面应力张量的3个分量。例如从ΔεⅢ、ΔεⅡ、ΔεⅠ求得水平主应力变化:
| $ \begin{array}{l} {\sigma _1} = \frac{1}{{4A}}\left( {\Delta {\varepsilon ^{\rm{I}}} + \Delta {\varepsilon ^{{\rm{III}}}}} \right) + \\ \;\;\;\;\;\;\;\frac{1}{{4B}}\sqrt {{{\left( {\Delta {\varepsilon ^{\rm{I}}} + \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2} + {{\left( {2\Delta {\varepsilon ^{{\rm{II}}}} - \Delta {\varepsilon ^{\rm{I}}} - \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2}} , \end{array} $ | (5) |
| $ \begin{array}{l} {\sigma _2} = \frac{1}{{4A}}\left( {\Delta {\varepsilon ^{\rm{I}}} + \Delta {\varepsilon ^{{\rm{III}}}}} \right) - \\ \;\;\;\;\;\;\;\frac{1}{{4B}}\sqrt {{{\left( {\Delta {\varepsilon ^{\rm{I}}} - \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2} + {{\left( {2\Delta {\varepsilon ^{{\rm{II}}}} - \Delta {\varepsilon ^{\rm{I}}} - \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2}} , \end{array} $ | (6) |
| $ \phi = \theta - \frac{1}{2}\arctan \frac{{\Delta {\varepsilon ^{\rm{I}}} + \Delta {\varepsilon ^{{\rm{III}}}} - 2\Delta {\varepsilon ^{{\rm{II}}}}}}{{\Delta {\varepsilon ^{\rm{I}}} - \Delta {\varepsilon ^{{\rm{III}}}}}}. $ | (7) |
从4个元件共有4种提取3个元件的组合方式,其余的ΔεⅡ、ΔεⅠ、ΔεⅣ,ΔεⅠ、ΔεⅣ、ΔεⅢ,和ΔεⅣ、ΔεⅢ、ΔεⅡ组合可以仿照式(5)~式(7)得到,然后计算平面应力变化的平均值,或者直接从方程组求最小二乘解。
| $ \begin{array}{l} {\sigma _1} = \frac{1}{{8A}}\left( {\Delta {\varepsilon ^{\rm{I}}} + \Delta {\varepsilon ^{{\rm{III}}}} + \Delta {\varepsilon ^{{\rm{II}}}} + \Delta {\varepsilon ^{{\rm{IV}}}}} \right) + \\ \frac{1}{{4B}}\sqrt {{{\left( {\Delta {\varepsilon ^{\rm{I}}} - \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2} + {{\left( {\Delta {\varepsilon ^{{\rm{IV}}}} - \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2}} , \end{array} $ | (8) |
| $ \begin{array}{l} {\sigma _2} = \frac{1}{{8A}}\left( {\Delta {\varepsilon ^{\rm{I}}} + \Delta {\varepsilon ^{{\rm{III}}}} + \Delta {\varepsilon ^{{\rm{II}}}} + \Delta {\varepsilon ^{{\rm{IV}}}}} \right) - \\ \frac{1}{{4B}}\sqrt {{{\left( {\Delta {\varepsilon ^{\rm{I}}} - \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2} + {{\left( {\Delta {\varepsilon ^{{\rm{IV}}}} - \Delta {\varepsilon ^{{\rm{III}}}}} \right)}^2}} , \end{array} $ | (9) |
| $ \phi = \theta - \frac{1}{2}\arctan \left( {\frac{{\Delta {\varepsilon ^{{\rm{IV}}}} + \Delta {\varepsilon ^{{\rm{II}}}}}}{{\Delta {\varepsilon ^{\rm{I}}} - \Delta {\varepsilon ^{{\rm{III}}}}}}} \right). $ | (10) |
从式(1)~式(4)可以导出的一个简单关系是,在图 1所示的观测条件下应满足下列自检条件
| $ \Delta {\varepsilon ^{\rm{I}}} + \Delta {\varepsilon ^{{\rm{III}}}} = \Delta {\varepsilon ^{{\rm{II}}}} + \Delta {\varepsilon ^{{\rm{IV}}}}. $ | (11) |
这一自检条件往往被简称为“1+3=2+4”,如果观察数据不满足该条件,则说明起码有一个或有更多元件的测量或标定出了问题。由于这种元件布设方法使得仪器的自检变得相对简易,促进了中国钻孔应变仪的改进和发展,20世纪70、80年代早期的钻孔应变仪往往不能满足自检条件,现在的观测大多数已能够满足自检条件。这种布设方法还可以在标定不是很好的情况下实现自我校准[7, 10],得到比较可靠的地应力观测资料。4个依次成45°夹角的四分量钻孔应变仪已成为中国具有创新特色的标准配置。国外的GTSM钻孔应变仪后来也加入第4个元件,它与第3个元件间隔30°,可以实现类似的功能,但自检表达式远不如“1+3=2+4”简单直接。
YRY-4型四分量钻孔应变仪是中国自主研发的四分量钻孔应变仪,其元件对应变的分辨力可达1×10-10。经过多年观测,YRY-4型四分量钻孔应变仪已取得一批可靠的观测数据[11]。钻孔应变观测数据的质量影响因素主要包括台站当地的地质环境、钻孔质量和附近的水温环境、应变仪布设、应变元件的耦合系数,以及当地是否有噪声源等多种因素。排除非构造因素的变化,找出构造应力的变化,对地震活动性评估具有重要意义。目前,对地应变观测资料的分析,往往侧重于地震之前观测到的一些异常[3],试图将前兆异常现象用于地震预报。然而了解分量式钻孔应变仪究竟记录的哪些是构造应力变化、哪些是非构造因素的影响,以及为什么会造成这样的影响,分析哪些是真正的构造应力异常,是需要深入研究的重要问题。地应力观测应成为地震物理预报的基础,而不是仅仅作为从曲线经验预报地震的一种手段。
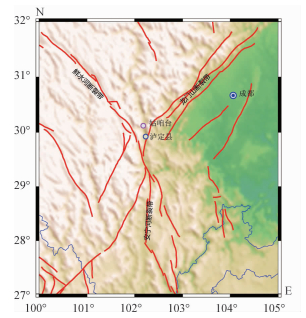
1 姑咱钻孔应变观测台站基本情况姑咱钻孔应变观测台站(30.12°N, 102.18°E)位于四川省甘孜藏族自治州康定县姑咱镇。地质构造上,台站位于NW-SE向鲜水河断裂带、NE-SW向龙门山断裂带和N-S向安宁河断裂带的交汇处以北处,龙门山断裂带西南延长线上[12](见图 2)。这一区域断裂活动性强烈,历史上曾多次发生中强以上的地震,如2008年汶川Ms8.0级地震[13-14],2013年芦山地震[15]均发生在龙门山断裂带,而鲜水河—安宁河断裂带自1480年至今发生过23次M≥6.5地震[16]。钻孔基岩为远古代黑云母花岗闪长岩[17],钻孔深40.69 m,由膨胀水泥与围岩固定。分量式钻孔应变仪4个径向位移传感器方位角(相对磁南北)分别为:52°、97°、142°和187°(见图 1)。考虑磁偏角(以成都磁偏角计算)为-1°09′,建立坐标系,以地理东为x轴,地理北为y轴,则四路传感器与x轴夹角分别为:39°、-6°、-52°和-96°。
|
Download:
|
| 图 2 姑咱台所处构造位置图 Fig. 2 Location and main faults around Guza borehole strain station | |
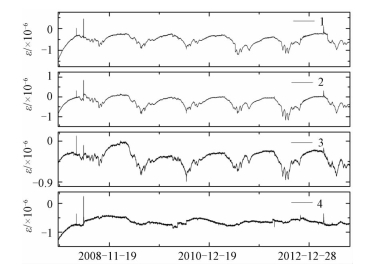
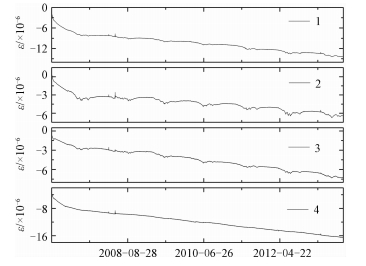
图 3为姑咱台四分量钻孔应变观测结果(2006年11月1日到2013年5月31日),4路元件数据均明显观测到长期的趋势性变化,呈现受到挤压缩短,并有明显的年周期变化。台站清楚地记录到固体潮,高频事件如2008年5月12日汶川地震在4个分量上也都被记录到,台站记录总体满足自检条件[15],说明记录可靠。记录第一年有较大的压缩量,可能与固定元件的膨胀水泥有关,随后的趋势性变化,有可能反映了地应力的长期变化。对台站观测数据滤波,剔除长年趋势性变化后的曲线如图 4所示。由图可见,除与大渡河流向相近的元件Ⅳ不太明显外,各元件存在明显的年度周期性变化,应变幅度可达10-6量级。影响四分量钻孔应变观测数据有多种因素[17-20],但这种年度变化,最大可能是由于山谷地区的地表温度变化引起,我们已经对此进行了热弹性有限元数值模拟[21]。另外每年雨季大渡河流量的大幅涨落期间,钻孔应变观测曲线会出现同步反向大幅度涨落的现象[22],这一现象尚未得到定量分析。因此本文将对水位变化对应变探头部位的应变和应力的影响进行有限元数值模拟研究,以便今后在分析中剔除非构造因素,了解构造应力的真实变化。
|
Download:
|
| 图 4 去除长年变化的姑咱台钻孔应变观测数据 Fig. 4 Data excluding long-term trend observed using Guza borehole strain meter | |
|
Download:
|
| 图 3 姑咱台四分量钻孔应变观测数据 Fig. 3 Data observed using four-component borehole strain meter of Guza station | |
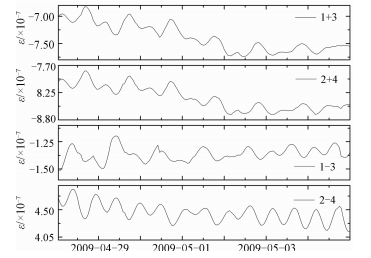
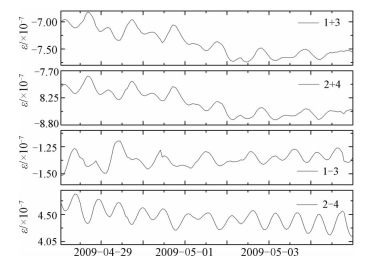
2009年5月1日至3日,姑咱台附近大渡河出现较大降水,降水后大渡河水位上涨5 m左右为例[17],这段时间的观测曲线如图 5。图 6为由图 5观测结果得到的从(1+4)与(2+3)曲线。从图 6可以看出(1+4)与(2+3)曲线形态一致,相关系数为0.997 2,说明观测结果可靠。
|
Download:
|
| 图 5 2009年4月28日0时至2009年5月5日0时4个元件的应变观测曲线 Fig. 5 Curves gauged by four components (28 April 2009 0:00-5 May 2009 0:00) | |
|
Download:
|
| 图 6 2009年4月28日0时至2009年5月5日0时1+3/2+4/1-3/2-4曲线 Fig. 6 The 1+3/2+4/1-3/2-4 curves(28 April 2009 0:00-5 May 2009 0:00) | |
通过24 h滑动平均去除固体潮影响后,求出4个元件涨水前后(4月29日0点到5月4日23点)的变化量。以接近东西向的元件Ⅱ受压最大,约为-300×10-10,元件Ⅳ受压最小,-188×10-10,元件Ⅰ和Ⅲ分别受压为-252×10-10和-235×10-10。根据式(1)~式(5)计算,得到岩体内应力变化Δσ1=-754 Pa,Δσ2=- 952 Pa, 主压应力方位角为88.3°,即接近东西方向为主压应力方向。
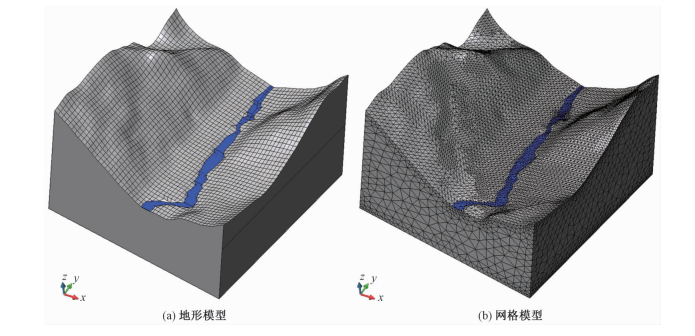
数值模拟模型取台站周围东西方向2 km,南北方向2 km,深度取为海拔600 m以上,地表考虑包含大渡河谷在内的地形因素。地形数据来源于中国科学院国际科学数据服务平台,本数据集利用ASTER GDEM第一版本(V1)的数据进行加工得来,数据精度30 m。以姑咱台为中心,将姑咱台东西、南北各1 km输入计算机中,通过Kriging插值,将2 km×2 km的地表数据分别分为50等份。地表处约40 m一个点(图 7(a))。姑咱台距大渡河330 m,大渡河宽约60 m。网格划分见图 7(b),共101 289个网格,21 009个节点。
|
Download:
|
| 图 7 模型计算网格图 Fig. 7 Numerical models and the grids | |
花岗岩的物性参数取值[23]如下:密度ρ为2 700 kg·m-3;杨氏模量E为70 GPa;泊松比υ为0.25。边界条件上表面为自由表面;4个侧面法向位移为0,垂向可以自由滑动(剪应力为0);底面垂直位移为0,切向可以自由滑动。河流水位涨后在图 7中蓝色河道部位,按其位置和水位雨季增加的高度施加垂向压力。
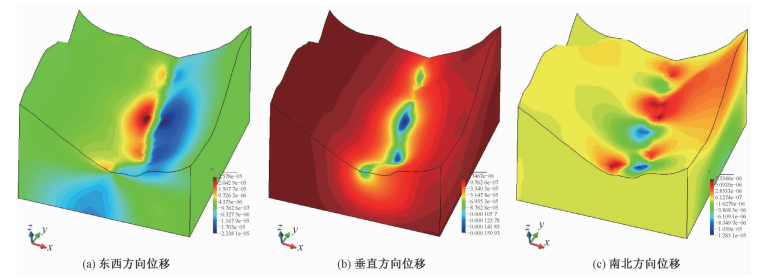
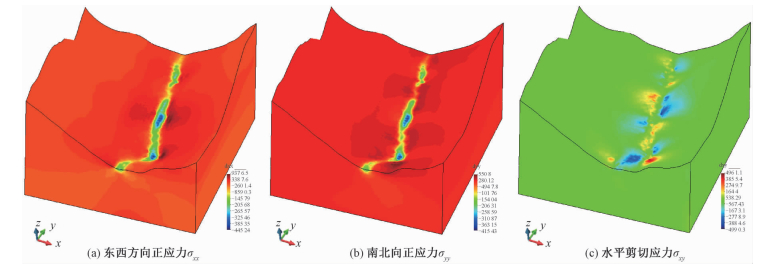
位移计算结果见图 8,其中图 8(a)为东西方向位移分量,位移的分布根据大渡河道的变化而变化,河西岸向东位移为正值,河岸东向西位移为负值;图 8(b)为垂直方向位移分量,位移沿大渡河大体成对称分布,河谷内位移最大,河谷宽的地方因增加的水的载荷最大而垂向下沉最大;南北向水平位移(图 8(c))很小,并且不规律,从计算结果来看,垂直方向位移总体最大,因此总体上位移分布以垂直方向位移为主。图 9为应力变化量计算结果图,如图所示,东西、南北方向应力沿大渡河道大体呈对称状分布(图 9(a)、9(b)),而水平剪切应力较小,且不规律(图 9(c)),这与河道两岸的地形有关。
|
Download:
|
| 图 8 涨水前后位移计算结果图 Fig. 8 Calculated surface displacements based on water level changes | |
|
Download:
|
| 图 9 涨水前后应力变化量计算结果图 Fig. 9 Calculated surface stress based on water level changes | |
根据模型计算在姑咱台元件位置处水位升高前和升高后应力变化量,结果为东西向水平应力变化量Δσxx=-598 Pa,南北向水平应力变化量Δσyy=-304 Pa,剪切应力变化量Δσxy=212 Pa。或者说,最小主应力(最大主压应力)为-710 Pa,最小主应力(最大主压应力)为-193 Pa,最大压应力方位角为73°,接近东西方向。由数值模拟结果看,由大渡河水位的增高,在姑咱台四分量钻孔应变仪元件,产生近kPa量级的应力变化,近东西向压应力分量变化最大。通过与实际观测值对比,计算值与观测值大体吻合。
3 讨论和结论通过数值模拟,计算得到大渡河水位变化对姑咱台四分量钻孔应变元件观测结果的影响,走向南北的河谷中河水涨落对河谷两侧的影响,造成东西向的挤压为主,计算值最大主压应力方位角为73°,与88°的观测值大体吻合。同时由于南北位移受约束而不能引张,也会有较小的挤压。计算结果表明,近南北向压力与近东西向压力的比大约等于泊松比,Δσ1/Δσ2=0.27,与该区计算模型中的泊松比0.25十分接近。最大主应力(最小主压应力)计算值Δσ1为-193 Pa,观测值为-754 Pa,最小主应力(最大主压应力)Δσ2为-710 Pa,实际观测值为-952 Pa。计算值和观测值虽然大体吻合,但计算的最大、最小主压应力均不及观测值。这可能是因为,我们计算的仅仅是河流水位升高的效应,但是降雨后,水渗入地下,全部地面都会受到附加的垂直载荷。由于不知道土壤、岩石风化层和地下水分布的具体资料,因此难以严格计算。但是如果是半无限空间受到均匀压力,假如有厚度为1 m的孔隙度为0.84的土壤或风化层饱含水,则在深部会造成约400 Pa的水平均匀压力。降水的作用曾有学者对其进行研究[24],把这一作用叠加到仅考虑河流水位影响的数值计算解之上,主压应力会分别增加到-592 Pa和-1 110 Pa,与观测值-754 Pa和-952 Pa的吻合还是令人满意的。计算对观测结果给出了合理的物理解释。
计算定量给出河水涨水的载荷对钻孔变形的影响,且与实际观测结果大体吻合。这使人们对大渡河涨水时,钻孔应变台站观测到压应力、特别是近东西向元件受到的压应力增加的感性认识,提高到定量化的理性认识。理论与观测结果的吻合有几方面的意义。一方面,说明水位变化的研究这种关系的确可以造成观测到的钻孔应变,在推断构造应力场变化及研究应力变化与地震活动性的联系时,应该把这种非构造成因的干扰扣除;而有限元数值计算有助于理解干扰的成因,定量地确定和排除非构造应力干扰因素。另一方面,这些结果也说明钻孔应变仪的确具有很高的灵敏度,不仅可以记录到固体潮这类全球性的变化,气压变化引起的区域性变化,而且可以观测到河流涨水这种局部载荷造成的地应力微小变化,证实了现在的地应力观测技术方法是可行和可靠的。再一方面,说明今后地应力台站选址建站时,应该尽量避开陡峭河谷地区,这种地区年度变化的水位变化的局部效应,以及年度温度效应[20],都会造成非构造应力变化,影响对区域构造应力场的观测和分析,尽管台站位置的选取要综合考虑地质构造、交通环境、电源保证等多方面因素,有时难以避免陡峭河谷,虽然可以在处理数据时采用一些修订方法,但最好还是在建站时就尽量考虑减少非构造因素的干扰,提高观测结果的信噪比。
2008年汶川大地震后,中国地震学界对地震研究进行了反思,一个重要的共识是,地震预报应该从以经验预报为主转变为大力发展物理预报方法。有的学者还提出真正的物理预报必须是基于数值模拟的数值预报。而数值预报的边界条件和初始条件的确定,计算结果的验证和应用,都需要开展地应力和地变形的观测和定量分析。钻孔应变仪的进一步推广和观测,有限元数值模拟技术的进一步深入和提高,对推动中国地震预报研究一定会发挥积极的促进作用。
| [1] |
邱泽华, 池顺良. YRY-4型钻孔应变仪观测的P波剪应变[J]. 地震, 2013, 33(4): 64-70. DOI:10.3969/j.issn.1000-3274.2013.04.007 |
| [2] |
Agnew D C. Strainmeters and tiltmeters[J]. Reviews of Geophysics, 1986, 24(3): 579-624. DOI:10.1029/RG024i003p00579 |
| [3] |
Linde A T, Gladwin M T, Johnston M J S, et al. A slow earthquake sequence on the San Andreas fault[J]. Nature, 1996, 383(6595): 65. DOI:10.1038/383065a0 |
| [4] |
Dewolf S, Wyatt F K, Zumberge M A, et al. Improved vertical optical fiber borehole strainmeter design for measuring Earth strain[J]. Review of Scientific Instruments, 2015, 86(11): 114502. DOI:10.1063/1.4935923 |
| [5] |
邱泽华, 石耀霖. 国外钻孔应变观测的发展现状[J]. 地震学报, 2004(S1): 163-169. |
| [6] |
石耀霖. 土应力测量[R]. 地质力学所技术报告03000号, 兰州: 地质力学所, 兰州地震大队地震地质队, 1971.
|
| [7] |
石耀霖, 范桃园. 地应力观测井中元件标定及应力场计算方法[J]. 地震, 2000, 20(2): 101-106. |
| [8] |
邱泽华, 石耀霖, 易志刚. 分量式钻孔应变观测数据的解释[J]. 地壳构造与地壳应力文集, 2002(14): 80-86. |
| [9] |
张凌空, 牛安福. 分量式钻孔应变观测耦合系数的计算[J]. 地球物理学报, 2013, 56(9): 3029-3037. |
| [10] |
Qiu Z, Tang L, Zang B, et al. In situ calibration of and algorithm for strain monitoring using four-gauge borehole strainmeters (FGBS)[J]. Journal of Geophysical Research Atmospheres, 2013, 118(4): 1609-1618. |
| [11] |
池顺良, 武红岭, 骆鸣津. 钻孔应变观测中潮汐因子离散性与各向异性原因探讨:"十五"数字地震观测网络分量钻孔应变仪首批观测资料分析解释[J]. 地球物理学进展, 2007, 22(6): 1746-1753. DOI:10.3969/j.issn.1004-2903.2007.06.010 |
| [12] |
邱泽华, 张宝红, 池顺良, 等. 汶川地震前姑咱台观测的异常应变变化[J]. 中国科学:地球科学, 2010(8): 1031-1039. |
| [13] |
Xu X, Wen X, Yu G, et al. Coseismic reverse-and oblique-slip surface faulting generated by the 2008 Mw 7.9 Wenchuan earthquake, China[J]. Geology, 2009, 37(6): 515-518. DOI:10.1130/G25462A.1 |
| [14] |
Der Hilst B. A geological and geophysical context for the Wenchuan earthquake of 12 May 2008, Sichuan, People's Republic of China[J]. GSA today, 2008, 18(7): 5. |
| [15] |
Xu X, Wen X, Han Z, et al. Lushan Ms 7.0 earthquake:a blind reserve-fault event[J]. Chinese Science Bulletin, 2013, 58(28/29): 3437-3443. |
| [16] |
Xueze W. Character of rupture segmentation of the Xianshuihe-Anninghe-Zemuhe fault zone, western Sichuan[J]. Seismology and Geology, 2000, 3(3): 60-64. |
| [17] |
阳光, 刘仕锦, 李学川. 姑咱台2008年汶川8.0级地震钻孔应变观测报告[J]. 地壳构造与地壳应力文集, 2010, 22: 135-148. |
| [18] |
董培育, 任天翔, 杨少华, 等. 钻孔应变观测同震阶变时的一个问题及对策分析[J]. 地质力学学报, 2015, 21(3): 359-370. DOI:10.3969/j.issn.1006-6616.2015.03.006 |
| [19] |
姚瑞, 杨树新, 王迪. 裂隙对四分量钻孔应力-应变观测影响的数值模拟分析[J]. 岩土工程学报, 2016, 38(2): 331-335. |
| [20] |
程惠红, 张怀, 朱伯靖, 等. 地应力测量中钻孔偏心分析[J]. 大地测量与地球动力学, 2011, 31(6): 164-169. |
| [21] |
杨少华, 任天翔, 董培育, 等. 姑咱台钻孔应变观测值年变化的数值模拟解释[J]. 地震地质, 2016, 38(4): 1137-1147. DOI:10.3969/j.issn.0253-4967.2016.04.026 |
| [22] |
邱泽华, 杨光, 唐磊, 等. 芦山M7.0地震前姑咱台钻孔应变观测异常[J]. 大地测量与地球动力学, 2015, 35(1): 61-66. |
| [23] |
Turcotte D L, Schubert G. Geodynamics[M]. Cambridge: Cambridge University Press, 2014.
|
| [24] |
王吉易, 宋贯一, 曹志成, 等. 地下水诱发的浅层前兆异常及其机理与有关的地震预报问题(3)[J]. 华北地震科学, 2002, 21(3): 28-41. |
 2018, Vol. 35
2018, Vol. 35 


