2. 中国科学院大学材料科学与光电技术学院, 北京 100049;
3. 天津中医药大学中药制药工程学院, 天津 300193
2. College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China;
3. College of Pharmaceutical Engineering of Traditional Chinese Medicine, Tianjin University of Traditional Chinese Medicine, Tianjin 300193, China
线型高分子链具有典型的统计分形特征,在其特征尺寸(如:回转半径Rg)与聚合度(N)的标度关系Rg ∝ Nν中,标度指数ν 通常为分数。作为高分子的基本物理性质之一,人们很早以前便对指数ν 的值进行了深入研究,发现它与高分子所处的溶剂环境有关。当高分子处于Θ溶剂中时,由于排除体积相互作用受到屏蔽,分子链会采取理想链构象,ν=0.5;而处于良溶剂中时,在排除体积相互作用的影响下,分子链构象遵循较为舒展的自回避行走,ν>0.5[1]。在理论研究方面,第一个对ν 值做出成功预测的理论是Flory给出的,通过构造简单的自由能模型(即Flory模型)给出ν=0.6[2],并且与实验符合很好[3];而更为复杂的重整化群方法则给出ν=0.588[1]。
值得指出的是,所谓的Θ溶剂是对应于某一溶剂在特定温度(即Θ温度)下的性质;而良溶剂则对应一定的温度范围,当温度在此范围内变化时,溶剂中的高分子链始终会感受到有限大小的排除体积相互作用。可以看到,在前述理论工作给出的物理图像中,对应于良溶剂的ν 值不随温度变化,这意味着指数ν 的值具有一定的普适性;依据这些经典理论的预测,从良溶剂温度达到Θ温度时,ν 值将从近0.6突变至0.5。这一观点在高分子科学领域被普遍接受,因而在很多实验及隐含溶剂的计算机模拟工作中,ν=0.6常被用作判断体系是否处于良溶剂状态的标准[4-5]。然而近年来,对于良溶剂中有限链长的接枝高分子单链的自洽平均场模拟发现,接枝链的高度与链长的标度关系指数具有温度依赖性[6];由于此标度关系应该与自由链的标度指数ν 一致,因此可以推断有限链长的自由链的ν 值同样与温度有关。事实上,Edwards[7]采用场论方法得到有限链长下高斯链模型的链尺寸与聚合度的依赖关系的渐进解,发现ν=0.6对应于渐进展开式的首项;这意味着,严格意义上ν=0.6仅适用于N → ∞的情形。
由于在实验和计算机模拟中的高分子链长是有限的,同时鉴于标度指数ν在高分子物理领域的重要地位,有必要详细考查有限链长下标度指数ν与溶剂性质的关系。本文采用自洽平均场理论对单链的平衡态性质进行考查,并选用实验和计算机模拟中易于测定的回转半径Rg作为高分子链的特征尺寸;同时为了克服应用自洽场理论计算Rg的固有困难,计算中结合蒙特卡洛模拟技术来实现对于高分子单链尺寸的统计。本文的重点在于不同溶剂中标度指数ν的取值,及其与溶剂性质的依赖关系。
1 模型与理论 1.1 自洽平均场理论采用高斯链模型描述高分子单链的构象,链长为Nb,其中b为统计学链段长度。高分子与溶剂的相互作用通过Flory-Huggins参量χ来表征,它在模型中同时具有温度的意义。由于高分子单链的运动同时包含整体平动和链段在分子链内部的相对运动(即构象变化),而链尺寸仅取决于后者;因此在模拟中,借鉴Edwards模型的方法将单链的一端固定于坐标空间的原点,从而排除高分子链整体平动对计算结果的影响。
由于自洽平均场理论的推导过程以及自洽场方程的数值解法在相关文献中已经有了详细的阐述[6, 8-9],在此仅对重要的方程和物理量进行重点描述。简言之,高斯链模型中的高分子链以一条连续的空间曲线R(s)代表,其中s=1,…,N;而高分子体积分数ϕP(r)可由末端传播子qf(r, s)和qa(r, s)导出,物理上它们代表高分子链在如下的等效场中的运动:
| $ {\omega _{\text{P}}}\left( \mathit{\boldsymbol{r}} \right) =-\ln \left( {1-{\phi _{\text{P}}}} \right)-2\chi {\phi _{\text{P}}}. $ | (1) |
原则上,通过对自洽场方程的求解可以得到高分子链的各种构象性质;特别是,回转半径Rg的表达式为
| $ \begin{gathered} R_{\text{g}}^2 = \left\langle {\frac{1}{{2{N^2}}}\int_0^N {{\text{d}}{s_1}} \int_0^N {{\text{d}}{s_2}} {{\left[{\mathit{\boldsymbol{R}}\left( {{s_1}} \right)-\mathit{\boldsymbol{R}}\left( {{s_2}} \right)} \right]}^2}} \right\rangle \hfill \\ \;\;\;\;\;{\text{ = }}\frac{1}{{{N^2}{Q_{\text{P}}}}}\int {{\text{d}}\mathit{\boldsymbol{r}}{\text{d}}\mathit{\boldsymbol{r'}}{{\left( {\mathit{\boldsymbol{r}} -\mathit{\boldsymbol{r'}}} \right)}^2}} \int_0^N {{\text{d}}s} \int_0^s {{\text{d}}s'} \times \hfill \\ \;\;\;\;\;\;\;{q^{\text{f}}}\left( {\mathit{\boldsymbol{r}}, N -s} \right)Q\left( {\mathit{\boldsymbol{r}}, s -s'|\mathit{\boldsymbol{r'}}} \right){q^{\text{a}}}\left( {\mathit{\boldsymbol{r'}}, s'} \right). \hfill \\ \end{gathered} $ | (2) |
式中:〈…〉表示系综平均;QP为单链配分函数;Q(r, s|r′)为单链传播子。qf(r, s)、qa(r, s)和Q(r, s|r′)均满足如下的修正扩散方程
| $ \frac{{\partial q}}{{\partial s}} = \left[{\frac{{{b^2}}}{6}{\nabla ^2}-{\omega _{\text{P}}}\left( \mathit{\boldsymbol{r}} \right)} \right]q. $ | (3) |
而相应的初始条件为:
| $ \begin{gathered} {q^{\text{f}}}\left( {\mathit{\boldsymbol{r}}, 0} \right) = 1, \hfill \\ {q^{\text{a}}}\left( {\mathit{\boldsymbol{r}}, 0} \right) = \delta \left( \mathit{\boldsymbol{r}} \right), \hfill \\ Q\left( {\mathit{\boldsymbol{r}}, 0|\mathit{\boldsymbol{r'}}} \right) = \delta \left( {\mathit{\boldsymbol{r}}-\mathit{\boldsymbol{r'}}} \right). \hfill \\ \end{gathered} $ |
式中,δ(r)为狄拉克δ-函数。可以看到,qa(r, s)和Q(r, s|r′)的初始条件具有很强的奇异性,从而为回转半径Rg的数值求解带来很大困难;因此,虽然Rg在实验和计算机模拟中被广泛用于表征高分子链的特征尺寸,但是在自洽场理论处理高分子系统的文献中很少被涉及和使用。
1.2 蒙特卡洛方法如前所述,在自洽平均场理论框架下,溶剂中高分子单链的构象可以看做是在一个等效场ωP(r)中的高分子单链的构象;通过求解自洽场方程可以很容易得到平衡态时等效场的数值解。同时为了回避单链传播子Q(r, s|r′)带来的固有的奇异性,这里采用单链平均场的思想[10-12],通过在等效场中用蒙特卡洛方法直接对高分子构象进行采样和统计,从而实现对构象相关物理量(特别是回转半径Rg)的统计求解。
具体地说,在本文的蒙特卡洛模拟中采用与自洽场理论中相同的高斯链模型,计算中将其离散为聚合度为N的珠簧模型,由自洽场方程求解得到的等效场ωP(r)则作为蒙特卡洛模拟中的外场。对随机选取的链珠做随机的位移Δr实现蒙特卡洛的尝试移动,并将105个尝试移动定义为一个蒙特卡洛步。通过metropolis算法判断该构象是否被接受。具体计算流程如图 1所示,对于给定的N和χ,首先通过求解自洽场方程得到等效场,之后进入蒙特卡洛模拟阶段;在进行系综平均前先令高分子单链于等效场中进行足够多步数的预跑(~105蒙特卡洛步),使高分子和平均场达到热平衡;之后进一步统计106蒙特卡洛步的高分子构象计算得到回转半径Rg。

|
Download:
|
| 图 1 计算流程示意图 Fig. 1 Flow chart of the simulation procedure | |
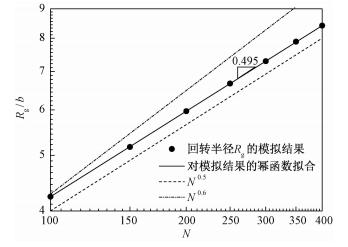
在自洽场理论框架下,溶剂的性质完全取决于Flory-Huggins参量χ的取值;特别是,χ=0.5代表Θ溶剂的情形,χ=0对应于通常所说的无热溶剂,而典型良溶剂通常满足0 < χ < 0.5。因此对于不同的χ值,分别考查回转半径Rg与聚合度N的标度关系,即可得到标度指数ν随溶剂性质变化而改变的规律。代表性的计算结果呈现于图 2~图 4中,图中同时给出对应于N0.6和N0.5的曲线以便于对比,模拟结果的误差棒小于图例的大小。计算中选取的链长N∈{100, 150, 200, 250, 300, 350, 400},皆为相关实验和计算机模拟工作中的典型链长值。
|
Download:
|
| 图 2 χ=0.5时Rg与N的依赖关系 Fig. 2 Rg as a function of N at χ=0.5 | |
|
Download:
|
| 图 3 χ=0时Rg与N的依赖关系 Fig. 3 Rg as a function of N at χ=0 | |
|
Download:
|
| 图 4 χ=0.3时Rg与N的依赖关系 Fig. 4 Rg as a function of N at χ=0.3 | |
图 2所示为χ=0.5,即Θ溶剂时由本文的模拟方法计算得到的Rg与N的依赖关系。为了方便标度关系的考查,这里采用双对数坐标对数据进行展示,并且在双对数坐标下通过对7个模拟数据点做直线拟合即可得到标度指数ν的值。从图上可以看到,对应于不同链长的数据点在双对数坐标下很好地落在一条直线上,说明至少在本文选取的链长范围内,Rg与N的依赖关系可以用标度关系Rg ∝ Nν来描述;通过最小二乘法拟合可得,标度指数ν=0.495±0.000(误差小于0.000 5),与理想链的结果(即0.5)非常接近。由此可知,自洽场理论框架下χ=0.5时高分子链确实遵循理想链的构象,同时也与相关实验和计算机模拟工作中所定义的Θ溶剂的情况相吻合。
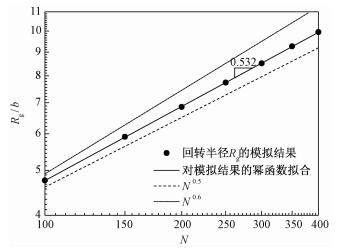
图 3展示的是χ=0时Rg与N的依赖关系数据,可以看到此时对于给定的聚合度N,Rg的值大于图 2中Θ溶剂的情形,这是由于良溶剂中排除体积相互作用的存在导致高分子链溶胀的结果。在双对数坐标下,各数据点依然可以用直线很好地拟合;拟合结果表明,标度指数ν=0.532±0.002。这一结果一方面说明,在χ=0时高分子单链构象明显偏离理想链构象;而另一方面也表明,此时高分子链的构象与经典理论中的自回避行走链(标度指数0.6)存在明显差异。值得指出的是,在应用自洽场理论处理高分子系统的相关工作中,人们通常认为χ=0对应于经典理论中的无热溶剂,并且认为此时的高分子链构象会遵循自回避行走链;然而这里的计算结果表明,在本文所选取的链长范围内,高分子链的构象行为实际上介于理想链和自回避行走链之间。
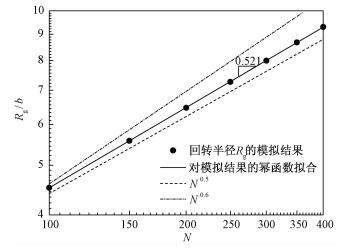
图 4呈现χ=0.3时Rg随N的变化趋势,此时溶剂性质属于通常所说的良溶剂情况。从图上可以看到,此时的拟合结果表明,标度指数ν=0.521±0.001,介于χ=0.5和χ=0两种情况之间;综合上述结果可知,对于本文选取的链长范围,ν值并非如经典理论预测中普适于各种良溶剂,而是会随着溶剂性质的变化发生改变。因此进一步计算得到不同χ值下的标度指数ν,结果汇总于图 5中,经典理论对于良溶剂中ν值的预测(即ν=0.588)也同时以虚线在图上标出以便比较。从图上可以看到,随着χ值的减小,良溶剂程度的加深,标度指数ν的值逐渐增大;总体上讲,由χ=0.5时的0.495到χ=0时的0.532的转变是一个平滑过渡的过程,并不存在经典理论预测中的突变情况。实际上,由图 5可见,虽然ν值随着良溶剂程度的加深而逐渐增大,但增大的速度非常缓慢;如果利用图 5的结果进行外推,需要

|
Download:
|
| 图 5 标度指数ν 与参量χ的依赖关系 Fig. 5 Dependence of the scaling exponent ν on Flory-Huggins parameter χ | |
为了探究模拟结果与经典理论之间产生上述偏差的原因,有必要在此回顾一下Edwards的相关研究成果。在文献[7]中,Edwards结合平均场近似得到良溶剂中高斯链的均方末端距〈R2〉的渐进表达式
| $ \begin{gathered} \frac{{\left\langle {{\mathit{\boldsymbol{R}}^2}} \right\rangle }}{{{N^{6/5}}{b^2}}} = {\left( {\frac{5}{3}} \right)^{6/5}}{\left( {\frac{{1-2\chi }}{{3\pi }}} \right)^{2/5}} + \hfill \\ {c_1}{\left( {1-2\chi } \right)^{1/5}}{N^{-1/10}} + {c_2}{N^{ - 1/5}} + \cdots . \hfill \\ \end{gathered} $ | (4) |
式中,c1和c2为渐进展开常系数。作为线型高分子的两个特征尺寸,Rg2应与均方末端距〈R2〉遵从相同的标度规律,因此可以预见Rg2也符合类似于方程(4)的渐进展开式;这意味着,Rg2随聚合度N的变化规律将按N-1/10的级数展开。这一方面表明,当N → ∞时,标度指数ν → 0.6;另一方面,这种趋势只有当N值很大时才能明显表现出来。事实上当N=400时,N-1/10 ≈ 0.55,N-1/5 ≈ 0.3,因此与首项相比方程(4)中的高阶项不可忽略;并且随着χ → 0.5,首项对方程(4)的贡献逐渐减小,而高阶项的影响反而逐渐突出。因此对于有限链长,当χ值增大时,即使溶剂性质还处于良溶剂范畴,标度指数ν的值也会明显偏离经典自回避链的情况。
3 结论本文采用自洽平均场理论并结合蒙特卡洛方法详细考查有限链长的高分子单链在Θ溶剂以及不同良溶剂中其回转半径Rg与聚合度N的依赖关系。计算结果表明,对于给定的溶剂条件(即χ值),Rg随N的变化可用标度关系Rg ∝ Nν来描述,然而标度指数ν并非普适常数,而是随着χ的改变发生变化。一方面,对于χ=0.5的Θ溶剂,ν值接近于0.5,说明此时的高分子链具有理想链构象,这与经典理论的预测一致;另一方面,对于χ < 0.5的各个良溶剂而言,ν值随着χ的减小平缓地增大,当χ=0时ν ≈ 0.532,依然与经典良溶剂理论的预测值0.6有明显的偏离。通过与相关模型的渐进解的对比发现,造成这种偏离的一个重要原因是“有限链长效应”。具体地说,经典理论对标度指数ν 的预测值0.6严格意义上是适用于无限长高分子链(即N → ∞);对于有限大的聚合度N,回转半径Rg可按N-1/10做渐进级数展开,于是针对102级大小的N值而言,高阶项的贡献不仅不可忽略,而且随着χ → 0.5愈加重要,此时若依然采取简单的标度关系来描述Rg随N的变化则标度指数ν 便会偏离经典理论的预测并且定量上呈现出对于溶剂性质的依赖性。
在实际应用中,人们常根据标度指数ν的值判断所用溶剂的优劣,但往往忽略有限链长效应。例如:在Grest和Murat的分子动力学模拟工作中[4],他们通过标度指数ν的值来确定体系的Θ温度以及良溶剂和劣溶剂所对应的温度范围;而在Elliott等的分子动力学模拟工作中[5],ν=0.6则被作为良溶剂的唯一判断标准。由本文的结果可知,将ν=0.5作为Θ溶剂的判断标准具有合理性,但是对于良溶剂而言却不存在普适的ν值。这一发现对于比较不同理论方法下的计算结果尤为重要。例如在文献[5]中,Elliott等将分子动力学模拟(对应于ν=0.6)的结果与χ=0时的自洽平均场理论计算结果比较后得出两种方法的结果存在定性差异的结论;然而对照本文的计算结果可知,对于他们所采用的聚合度N值(均小于200)而言,χ=0时的自洽平均场理论计算与ν=0.6时的分子动力学模拟实际上针对着不同温度下的体系,必然会存在差异。因此,当计算机模拟结果与自洽平均场理论的计算作比较时,有必要首先通过计算确定各自体系的标度指数ν以便保证体系的一致性;而在自洽场理论框架下ν值的计算可以通过本文所报道的方法有效地实现。
值得一提的是,本文的研究没有涉及不良溶剂(χ>0.5)的情形,这是因为考虑到以往相关的实验和模拟工作多以良溶剂和Θ溶剂为主。理论上,χ 值的增大将导致高分子链的进一步坍缩,以及标度指数ν的进一步减小,其下限将是1/3(即刚体的数值),因此对于不良溶剂,可以预见1/3 < ν < 0.5;而技术上,本文的计算方法可以直接用于不良溶剂的情形,对于这些的模拟将是下一步工作的重要内容。
| [1] |
Rubinstein M, Colby R H. Polymer physics[M]. Oxford, UK: Oxford University Press, 2003: 102-104.
|
| [2] |
Flory P J. Principles of polymer chemistry[M]. Ithaca, New York: Cornell University Press, 1953: 29-66.
|
| [3] |
Fetters L J, Hadjichristidis N, Lindner J S, et al. Molecular weight dependence of hydrodynamic and thermodynamic properties for well-defined linear polymers in solution[J]. J Phys Chem Ref Data, 1994, 23(4): 619-640. DOI:10.1063/1.555949 |
| [4] |
Grest G S, Murat M. Structure of grafted polymeric brushes in solvents of varying quality:a molecular dynamics study[J]. Macromolecules, 1993, 26(12): 3108-3117. DOI:10.1021/ma00064a019 |
| [5] |
Elliott I G, Kuhl T L, Faller R. Molecular simulation study of the structure of high density polymer brushes in good solvent[J]. Macromolecules, 2010, 43(21): 9131-9138. DOI:10.1021/ma101252c |
| [6] |
Suo T, Whitmore M D. Self-consistent field theory of tethered polymers:one dimensional, three dimensional, strong stretching theories and the effects of excluded-volume-only interactions[J]. J Chem Phys, 2014, 141(20): 204903. DOI:10.1063/1.4901925 |
| [7] |
Edwards S F. The statistical mechanics of polymers with excluded volume[J]. Proc Phys Soc, 1965, 85: 613-624. DOI:10.1088/0370-1328/85/4/301 |
| [8] |
Suo T, Yan D. Theoretical study on tethered polymers with explicit grafting points in Θ-solvent[J]. J Chem Phys, 2011, 134(5): 054901. DOI:10.1063/1.3549911 |
| [9] |
Matsen M W. Self-consistent field theory and its applications[C]//Gompper G, Schick M. Soft Matter. Weinheim: Wiley-VCH Verlag GmbH & Co. KGaA, 2007: 7-11.
|
| [10] |
Tang J, Zhang X, Yan D. Compression induced phase transition of nematic brush:a mean-field theory study[J]. J Chem Phys, 2015, 143(20): 204903. DOI:10.1063/1.4936324 |
| [11] |
Fu J, Zhang X, Miao B, et al. Light-responsive expansion-contraction of spherical nanoparticle grafted with azopolymers[J]. J Chem Phys, 2017, 146(16): 164901. DOI:10.1063/1.4981914 |
| [12] |
Xu G, Huang Z, Chen P, et al. Optimal reactivity and improved self-healing capability of structurally-dynamic polymers grafted on janus nanoparticles governed by chain stiffness and spatial organization[J]. Small, 2017, 13(13): 1603155. DOI:10.1002/smll.v13.13 |
 2018, Vol. 35
2018, Vol. 35 


