2. 北方电子设备研究所, 北京 100083;
3. 中国科学院心理研究所, 北京 100101
2. Institute of Northern Electronic Equipment, Beijing 100083, China;
3. Institute of Psychology, Chinese Academy of Sciences, Beijing 100101, China
人格是心理学概念,研究的是人性的内容,指的是人类心理特征的整合与统一,是相对稳定的组织结构,并在不同时间、地域影响着人的内隐心理特征和外显行为模式。目前应用最广、最可靠、最主流的人格特质模型是心理学界公认的大五人格模型,该模型通过5维向量(N, A, E, C, O)描述人格[1],分别代表神经质、宜人性、外向性、尽责性和开放性。每个维度从不同侧面描述一个人的人格。
当前,随着新型信息技术的快速发展和社交网络的大范围应用,利用社交网络进行用户人格预测已经成为研究热点。国外研究者主要是利用Facebook、Twitter等社交网络对用户人格进行预测,国内主要通过新浪微博、人人网等社交平台对用户进行人格预测。
国内外研究学者对社交网络用户的大五人格预测,大都采用回归或分类等机器学习算法。不同点主要在于针对不同的社交网络,提取多样的属性数据。主要可分为两类:
一类是从社交网站提取的行为特征,包括静态特征、动态特征和文本特征。静态特征是指随时间不变化或者变化慢的数据特征,如性别、年龄、粉丝数、朋友数等;动态特征是指随时间容易变化的数据特征,如转发、收藏、点赞等;文本特征是指提取文本中的数据特征,如@数、链接数、第一人称使用率等。
Ortigosa等[2]对Facebook用户社交数据采用朴素贝叶斯和C4.5算法,对5种人格维度进行预测建模。Wald等[3]通过对Twitter用户进行人格分析,采用逻辑回归、多层感知器、随机森林和SVM等方法,最终得出结论,不同的方法在进行人格预测时,结果相差不大,实验AUC指标结果在0.7左右。Li等[4]采用基于5折交叉验证算法训练SVM模型和PaceRegression模型,并且在模型训练过程中,为改善SVM性能,使用网络搜索算法进行参数调整。Wald等[5]对Facebook用户采用线性回归、RepTree以及决策表等算法进行人格预测,可预测出约74.5%的用户。这些方法通过提取社交网络用户的静态特征、文本特征以及动态特征中的一类或者多类特征,进行训练,利用监督学习方法进行分类和回归,进行用户的人格预测。并且也有结果表明,使用监督学习方法中不同的分类算法,最终效果相差不大[6]。
另一类是通过发布的文本内容的语义进行预测。通过语义分析出用户的情感、观点、意见以及人格魅力等信息[7]。但是通过文本信息研究的与人格特质相关的语料库的不同,严重限制人格的预测结果,很多研究者针对某一语料库进行的预测结果准确率能达到83%,然而当扩大语料库,准确率会迅速降到55%[8]。针对这一情况,Iacobelli等[7]通过使用一种大规模的语料库,采用回归及排序算法对各种文本特征提取进行比较,从分类准确率与基准回归算法相比提高的百分比以及排序算法的误差3个角度进行验证,预测结果都有很大提高。
综上所述,虽然通过社交网络对用户进行人格预测已取得很多研究成果,但其研究方法仅仅局限于单任务机器学习,即只是对某一种任务数据集进行训练,进而学习该任务的相关信息。然而,人格是从不同角度不同方面对个体进行的刻画,比如大五人格模型是从5个方面阐述人格:神经质特性从个体对事物的消极情绪的倾向反映其情绪化程度的调节能力;宜人性从个体对他人的态度方面反映其与人相处及协作的能力;外向性从个体人际互动的数量及频率反映其对刺激的需求及获得愉悦的能力;尽责性从个体控制、管理和调节自身冲动的方式,反应其在目标导向行为上的组织和坚持能力;开放性从个体的想象力及求知欲反映其智慧水平。
大五人格模型涵盖人格描述的主要方面,而且这5个维度之间往往不是完全孤立的,而是存在着某些关联性。在社交网络用户的大五人格预测方面存在以下两个问题:第一,从统计结果上看,一些人格维度之间存在一定的相关性。如宜人性得分较高的个体,其开放性得分也偏向较高。而另一些维度之间则更多表现为相互独立,如责任感与神经质之间、宜人性与开放性之间。这种人格维度之间的客观规律导致现有的人格预测模型不够理想。第二,现实中,获取大量而有效的社交网络用户的人格数据,是非常困难的,这样不可避免造成训练样本的缺乏。
因此,为了完整全面地对个体的人格进行预测,必须充分考虑5种人格维度之间可能存在的相关性。另一方面,训练样本不充分,极易造成模型的过拟合现象。针对这两种情况,可以将5种人格维度预测看成5类任务,通过并行学习这5类任务,充分利用任务之间的相关信息,这种思想正是多任务学习方法的核心;而多任务学习在提高小样本问题的学习性能上提出了合理的解决方案。
但是多任务学习前提是基于所有任务之间都存在相关性这一很强的假设,而微博用户大五人格的5个维度之间还存在上面提到的第2个问题,即五种人格维度中并不是所有任务都存在相关。因此为了避免不相关任务带来不好的效果,本文引入鲁棒多任务学习模型预测新浪微博用户人格,既共享多个任务之间的相关信息,又能识别出不相关任务。鲁棒的多任务学习目标就是寻找任务和特征之间的关联矩阵W。首先,通过正则化优化方法将多任务学习问题转换为优化问题;其次,引入混合范数、迹范数和L1/L2范数作为正则项约束,一个用于约束相关性,一个用于识别不相关任务;最后,通过求解正则约束的优化问题取得关联矩阵W的最优解。本文通过对获取的994名新浪微博被试者的微博数据样本进行训练,采用多任务学习方法,创建人格预测模型,并与单任务学习算法进行比较,结果显示多任务学习方法明显优于单任务学习效果。
1 相关工作目前基于社交网络预测分析人格过程中用到的机器学习都是单任务的分类或回归算法, 即将5种人格维度预测当作独立的5个分类或回归任务,分别进行建模。这样在训练数据不充足的情况下,极易造成过拟合而导致较差的泛化性能。同时由于五种任务之间存在着相关性,因此采用多任务学习方法,即充分利用任务之间的相关信息,又解决了小样本带来的训练过拟合现象。
1.1 多任务学习方法现实生活中,许多问题都是相关的,同样,机器学习领域,在解决分类或回归问题时,大部分也都是针对多个相关的任务。1997年Caruana首先提出多任务学习的方法[9],目的是通过学习与目标任务相关的多个任务实现对目标任务的学习。并考虑到不同任务之间的差异性,同时利用多个任务之间的数据特征,解决独立学习任务数据规模小的问题,为目标任务提供更加精确的知识。现在很多研究也证明了这一点[9-12],因此现在多任务学习算法成为众多领域研究热点[13-16]。
多任务学习从任务挖掘上来讲,主要有两种:
第一种是从数据样本特征中挖掘具有相同特征的任务。如Argyriou等[10]基于训练数据特征之间的相关性,利用矩阵的L1,2范数进行正则化表示,约束学习任务的低秩结构,将训练数据特征划分为不同的子任务,从而使多个任务共享同一个低维子空间,实现特征之间潜在信息的共享。文献[16]基于训练数据特征之间的相关性,通过使用线性SVMs和多任务学习方法,提出一种高效的非线性数据分类器LSVM-MTL模型,充分利用相关任务中包含的有用信息,改善了每个任务的SVM的分类性能。
第二种是从目标任务中挖掘具有相关性的任务。如白朔天等[17]采用多任务回归的方法采集社交媒体中用户行为数据,分析用户5种人格维度与网络行为之间的关系,通过训练模型,采用最小平方和损失和Frobenius泛数进行建模,确定使预测值和标注值之差最小的传递矩阵,实现社交网络数据和人格维度之间的模型创建。
多任务学习的方法研究主要集中在模型上,提出不同的模型假设,总结出新的多任务学习方法,包括共享变量、共享子空间以及共享模型参数等,将这些共享的有价值信息,作为每个任务学习的辅助信息,以此提升学习效果。具体从实现方法上来讲,主要有两种:
第一种方法是加入正则项进行约束学习。正则项(也称作惩罚项)约束方法,通过引入关联矩阵的不同种类的范数约束任务之间特征的相关性,将多任务学习问题转化为优化问题,取得其最优解。Evgeniou和Pontil[18],提出均值正则化多任务学习,在核空间使用范数约束获得任务之间的共享结构,通过假设每个任务都近似,最小化独立部分,使得学习到的结果都与公共部分相似,进行任务之间关联性建模,其参数模型为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}} = \arg \mathop {\min }\limits_W \left( {L\left( {\mathit{\boldsymbol{Y}},{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right) + \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^m {{\xi _{it}}} } + } \right.}\\ {\left. {\frac{{{\lambda _1}}}{T}\sum\limits_{t = 1}^T {{{\left\| {{v_t}} \right\|}^2}} + {\lambda _2}{{\left\| {{w_0}} \right\|}^2}} \right).} \end{array} $ |
式中:L(·)是损失函数;W=[w1, …, wT]为模型参数矩阵,对应T个任务;ξit为添加的松弛变量;w0为模型参数的平均值。该模型的假设前提是所有模型参数均服从正态分布,且都在均值附近,vt为各任务模型参数与均值之间的距离。模型第3项用来控制模型复杂度的正则项,最后一项是用来约束任务的模型参数与模型均值的距离,这样就使得所有任务尽可能得相似,从而将单任务的SVM算法转移为多任务SVMs算法。最后通过模拟数据和真实数据的实验,论证了多任务SVM模型比单任务SVM要好很多。
第二种方法是贝叶斯方法,通过对参数W的协方差矩阵的贝叶斯学习实现参数的更新和估计,利用协方差矩阵的相关系数确定多个任务之间的相关关系。Zhang和Yeung[12]提出一种新的贝叶斯扩展模型用于解决协方差矩阵估计过程中出现的问题。
多任务学习的过程就是每个任务分别学习各自的结果,但是在学习过程中被联合在一起,使得信息之间可以传递共享。其核心就是挖掘数据特征与任务构成的参数关联矩阵之间的相关性,可以通过数据特征之间、任务之间、约束条件和损失函数、样本之间的连接结构和任务残差等方面,作为信息传递渠道,共享有价值的信息,将多个不同的学习任务纳入一个决策模型中,从而提高预测精度。
1.2 鲁棒多任务学习方法多任务学习主要是基于多个任务之间是相关的这一很强的假设,而这一假设忽略了任务中的离群任务的存在。鲁棒的多任务学习(robust multi-task learning,RMTL)方法[19-23]将这些不相关的任务作为异常来处理。一般鲁棒多任务学习方法都是将任务分成相关任务和异常任务两种情况进行处理,通过将参数模型进行分解,分解为结构项和异常项进行多任务建模,然后通过添加正则化项进行约束,求解多任务学习最优解。
文献[20]考虑到一些异常任务,将参数模型分解为两部分,W=P+Q,即将关联矩阵W分成两个部分,表示通常的相关任务和异常的任务,分别是低秩结构P和组稀疏结构Q,P用来捕捉相关任务信息,Q用来检测异常任务信息。因此正则化项也相应分解为两部分,并使用不同的正则项来约束相关任务和异常任务,模型如下所示
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}} = \arg \mathop {\min }\limits_{W = P + Q} \left( {L\left( {\mathit{\boldsymbol{Y}},{{\left( {\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{Q}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right) + } \right.}\\ {\left. {{\rho _1}{{\left\| \mathit{\boldsymbol{P}} \right\|}_{2,1}} + {\rho _2}{{\left\| \mathit{\boldsymbol{Q}} \right\|}_{1,2}}} \right).} \end{array} $ |
文献[21]提出一种鲁棒的多任务回归学习方法,添加两项正则项用于处理高维稀疏数据造成的总误差(sparse gross errors),响应矩阵Y∈Rn×q,协方差矩阵X∈Rn×p,其回归模型:
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{X}}{\Theta ^ * } + \mathit{\boldsymbol{W}} + {\mathit{\boldsymbol{G}}^ * } $ |
式中:Θ*∈Rp×q为预测值和响应值之间的未知线性关系;W∈Rn×q为噪声矩阵;G*为相对于sparse gross errors的矩阵。采用Frobenius范数、L1范数以及L2范数进行建模计算,从误差角度对多任务回归进行建模,提高模型的鲁棒性。
文献[22]将权重矩阵分解为两部分,同时使用Lasso方法处理相关任务,使用group Lasso方法处理异常任务,采用加速梯度算法来解决多任务学习的优化问题,提高算法的鲁棒性。
也有研究者通过任务协方差矩阵建模,Yu等[19]提出一种基于t过程的鲁棒的贝叶斯多任务学习框架,t过程是高斯过程的一种推广,能够将异常任务很好地分辨出来,使用广义t噪声模型作为似然函数与广义t过程先验结合,从而提高算法的鲁棒性。
对任务协方差矩阵建模的过程中,往往会使用到非参数方法,从而使得该方法计算量非常的大。因此本文将基于正则项约束求解方法解决鲁棒的多任务学习问题。
2 基于RMTL的微博用户大五人格预测建模 2.1 问题描述假设有T个目标任务,属于空间X×Y,其中X⊂Rd, Y⊂R,这里T=5,对应于大五人格的5种人格维度预测,即(O, A, E, C, N)5个任务。对于每一个任务,有n个数据,则对于任务t,其训练数据样本表示如下所示:
| $ \left\{ {\left( {{x_{t1}},{y_{t1}}} \right),\left( {{x_{t2}},{y_{t2}}} \right), \cdots ,\left( {{x_{tn}},{y_{tn}}} \right)} \right\}, $ |
式中:(xti, yti)表示任务t中用户i的实例对,其中xti表示第i个用户的样本向量,yti表示用户i的任务t的标签,是一个值。那么T个任务的训练数据样本表示如下所示:
| $ \begin{array}{*{20}{c}} {\left\{ {\left\{ {\left( {{x_{11}},{y_{11}}} \right), \cdots ,\left( {{x_{1n}},{y_{1n}}} \right)} \right\}, \cdots ,} \right.}\\ {\left. {\left\{ {\left( {{x_{T1}},{y_{T1}}} \right), \cdots ,\left( {{x_{Tn}},{y_{Tn}}} \right)} \right\}} \right\}} \end{array} $ |
因此,新浪微博用户大五人格预测的目标就是学习5个函数,如下
| $ {f_i},{f_2}, \cdots ,{f_T},{f_t}\left( {{x_{it}}} \right) = {\mathit{\boldsymbol{X}}_{it}}{w_t} \approx {y_{it}}. $ | (1) |
式中:t=1, 2, …, 5,每个函数代表一种人格维度的预测模型。
对于每种人格预测任务来说,学习的目标最终转化为参数wt的优化求解,如下
| $ {w_t} = \arg \min L\left( {{X_t},{y_t},{w_t}} \right) + \lambda \Omega \left( {{w_t}} \right). $ | (2) |
式中:wt∈Rn为模型参数;L(·, ·)为训练数据集上的损失函数;Ω(wt)为参数wt的正则化项;λ为正则化参数,用于平衡损失函数和正则化项。在单任务学习中,添加正则化项的目的是使模型避免数据过拟合,保证模型得到最小化训练误差。
本文提出的基于多任务学习的新浪微博的大五人格预测问题,相当于并行学习5种人格预测,因此输入矩阵X、输出矩阵Y以及关联矩阵W分别如下所示:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Y}} = \left( {\begin{array}{*{20}{c}} {{y_{11}}}& \cdots &{{y_{1n}}}\\ \vdots &{}& \vdots \\ {{y_{T1}}}& \cdots &{{y_{Tn}}} \end{array}} \right),\mathit{\boldsymbol{X}} = \left( {\begin{array}{*{20}{c}} {{x_{11}}}& \cdots &{{x_{1n}}}\\ \vdots &{}& \vdots \\ {{x_{d1}}}& \cdots &{{x_{dn}}} \end{array}} \right),}\\ {\mathit{\boldsymbol{W}} = \left( {\begin{array}{*{20}{c}} {{w_{11}}}& \cdots &{{w_{1d}}}\\ \vdots &{}& \vdots \\ {{w_{T1}}}& \cdots &{{w_{Td}}} \end{array}} \right)} \end{array} $ |
这样基于多任务学习方法的大五人格预测的目标,则表示为
| $ f\left( \mathit{\boldsymbol{X}} \right) = \mathit{\boldsymbol{WX}} \approx \mathit{\boldsymbol{Y}}. $ | (3) |
多任务学习目的就是学习模型参数矩阵W,矩阵中行表示每个任务的特征向量,列表示某种特征属性。同样利用损失函数和正则化项进行建模,寻找参数矩阵W中列之间的关系或者行之间的关系,从而实现多个任务之间的并行学习,同时避免训练过程中的过拟合现象,提高模型的泛化性能。
2.2 模型建立基于多任务正则化方法的新浪微博大五人格预测目标如公式(3)所示,最终通过添加正则化约束,实现多个任务之间特征相关性的学习,将目标转化为优化求解公式
| $ \mathit{\boldsymbol{W}} = \arg \mathop {\min }\limits_W L\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{W}}} \right) + \lambda \Omega \left( \mathit{\boldsymbol{W}} \right). $ | (4) |
式中:W=[w1, w2,…, wt]∈Rn×t;Ω(W)为正则项,用于约束特征之间的相关性;λ为正则项系数,用于平衡损失函数与正则项。正则项通常用范数来实现,如最小化矩阵W的非零行问题实现矩阵的组稀疏表示[23],一般用L1范数实现,
| $ \mathit{\boldsymbol{W}} = \arg \mathop {\min }\limits_W L\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{W}}} \right) + \lambda {\left\| \mathit{\boldsymbol{W}} \right\|_1}. $ | (5) |
如矩阵的低秩表示[24],采用核范数进行约束,
| $ \mathit{\boldsymbol{W}} = \arg \mathop {\min }\limits_W L\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{W}}} \right) + \lambda {\left\| \mathit{\boldsymbol{W}} \right\|_ * }. $ | (6) |
社交网络用户大五人格预测学习过程中,其中大五人格模型是使用统计学方法研究出来的人格特质理论,能够全面描述人的人格特征,且五维度内部之间的关系稳定且仅存在一定的相关性。采集的新浪微博用户的人格标签数据显示(如图 1),宜人性较高的得分个体其尽责性的分也偏向较高;神经质特征得分较高的个体,其宜人性特征得分偏向较低;而神经质与开放性以及开放性与宜人性之间并不存在显著相关,也就是说新浪微博用户大五人格从得分数据上看,既存在着相关性,也存在不相关性,因此使用一般的多任务正则化模型难以实现预测的效果的提高,相反可能会带来更差的效果。
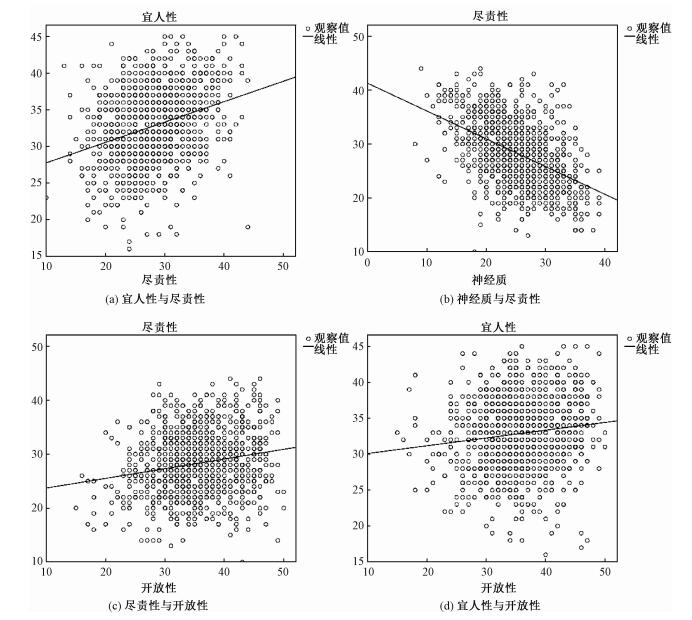
|
Download:
|
| 图 1 人格维度之间的关系 Fig. 1 Relationship between the Big-Five personality dimensions | |
针对这种现象,采取能够识别异常任务存在的鲁棒多任务学习方法,进行社交网络用户大五人格的建模,将参数模型进行分解,分解为一个结构项和一个异常项。正则化项也对应地分解为两项,分别是结构信息和异常结构信息,既能识别模型的共性,共享隐藏的信息,也能检测出不相关任务信息,避免不相关任务之间的相互影响。
因此对于T个任务的模型关联矩阵W,W=[w1, w2, …, wt]∈Rd×t,将被分为两部分W=P+Q,P用于约束低秩,挖掘任务之间的相关性,Q用于约束组稀疏,识别出不相关任务,其中:
| $ \begin{array}{l} \mathit{\boldsymbol{P}} = \left[ {{p_1},{p_2}, \cdots {p_t}} \right] \in {{\bf{R}}^{d \times t}}\\ \mathit{\boldsymbol{Q}} = \left[ {{q_1},{q_2}, \cdots {q_t}} \right] \in {{\bf{R}}^{d \times t}} \end{array} $ |
采用最小平方损失函数和核范数、L1/L2范数进行建模,则微博用户大五人格预测模型的目标函数可表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}} = \mathop {\min }\limits_{W = P + Q} \sum\limits_{i = 1}^T {\left\| {\mathit{\boldsymbol{W}}_i^{\rm{T}}{X_i} - {Y_i}} \right\|_{\rm{F}}^2} + }\\ {{\rho _1}{{\left\| \mathit{\boldsymbol{P}} \right\|}_ * } + {\rho _2}{{\left\| \mathit{\boldsymbol{Q}} \right\|}_{1,2}}.} \end{array} $ | (7) |
式中:Wi为第i个任务的模型参数;Xi为第i个任务的训练数据集;Yi为第i个任务标签数据;ρ1, ρ2是正则化参数;ρ1用于控制低秩正则项矩阵P,ρ2用于控制矩阵Q的L1, 2范数。
矩阵P的核范数表示为
| $ {\left\| \mathit{\boldsymbol{P}} \right\|_ * } = \sum\limits_{i = 1}^r {{\sigma _i}\left( \mathit{\boldsymbol{P}} \right)} , $ | (8) |
式中:r是矩阵P的秩,σi(P)为矩阵P的奇异值,核范数能够实现矩阵的稀疏表示,因此可以挖掘任务的相关性。
矩阵Q的L1, 2范数表示为
| $ {\left\| \mathit{\boldsymbol{Q}} \right\|_{12}} = \sum\limits_{i = 1}^d {{{\left\| {{q_i}} \right\|}_2}} , $ | (9) |
即为矩阵列向量的L2范数之和。L1, 2范数能够实现变量组水平上的稀疏性,具有变量组选择能力,利用L1, 2范数目的是辨别出异常任务。因此针对结构项矩阵P与异常任务矩阵Q,对应使用核范数与L1, 2范数进行约束学习,将多任务学习问题转化为求解正则约束的优化问题。
2.3 模型求解近端梯度求解正式针对minf(x)+h(x)形式的优化问题求解。对于式(7),
设平滑项
| $ f\left( \mathit{\boldsymbol{W}} \right) = L\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{W}}} \right) = \sum\limits_{i = 1}^T {\left\| {\mathit{\boldsymbol{W}}_i^{\rm{T}}{X_i} - {Y_i}} \right\|_{\rm{F}}^2} , $ | (10) |
设非平滑项
| $ h\left( \mathit{\boldsymbol{W}} \right) = {\rho _1}{\left\| \mathit{\boldsymbol{P}} \right\|_ * } + {\rho _2}{\left\| \mathit{\boldsymbol{Q}} \right\|_{1,2}}. $ | (11) |
近端梯度算法得到迭代公式为
| $ {W_{k + 1}} = {\rm{Pro}}{{\rm{x}}_{{\gamma _k},h}}\left( {{W_k} - {\gamma _k}\nabla f\left( {{W_k}} \right)} \right), $ | (12) |
式中:
对于凸函数h(W),其近端算子为
| $ {\rm{pro}}{{\rm{x}}_h}\left( \mathit{\boldsymbol{W}} \right) = \arg {\min _u}\left( {h\left( u \right) + \frac{1}{2}\left\| {u - \mathit{\boldsymbol{W}}} \right\|_2^2} \right). $ | (13) |
因此对于式(12),即变为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{k + 1}} = \arg \min \frac{{{\gamma _k}}}{2}\left\| {\mathit{\boldsymbol{W}} - \left( {{{\mathit{\boldsymbol{\hat W}}}_k} - \frac{1}{{{\gamma _k}}}\nabla f\left( {{\mathit{\boldsymbol{\hat W}}_k}} \right)} \right)} \right\|_{\rm{F}}^2 + }\\ {{\rho _1}{{\left\| {{\mathit{\boldsymbol{P}}_w}} \right\|}_ * } + {\rho _2}{{\left\| {{\mathit{\boldsymbol{Q}}_w}} \right\|}_{1,2}}.} \end{array} $ | (14) |
采用线搜索策略确定梯度下降的步长γk,其中用到第k步搜索点值表示为
加速近端梯度算法求解步骤:
输入:Xi:第i个任务的训练数据矩阵;
yi:第i个任务的人格标签向量。
1:初始化γk,β∈(0, 1)
2:γ=γk
3:do
4:设Z=proxγh(
5:break if
| $ \begin{array}{*{20}{c}} {l\left( {{\mathit{\boldsymbol{W}}_{k + 1}}} \right) \le l\left( {{{\mathit{\boldsymbol{\hat W}}}_k}} \right) + \left\langle {\nabla l\left( {{{\mathit{\boldsymbol{\hat W}}}_k}} \right),{\mathit{\boldsymbol{W}}_{k + 1}} - {{\mathit{\boldsymbol{\hat W}}}_k}} \right\rangle + }\\ {\frac{{{\gamma _k}}}{2}\left\| {{\mathit{\boldsymbol{W}}_{k + 1}} - {{\mathit{\boldsymbol{\hat W}}}_k}} \right\|_F^2} \end{array} $ |
6:更新步长γ=βγ
7:while γk+1=γ Wk+1=Z.
本文将采用加速近端梯度算法进行多任务学习优化求解[20]。加速近端梯度算法通过在搜索步长的过程中增加一步外插值操作,其算法是:
| $ {\mathit{\boldsymbol{Z}}_{k + 1}} = {\mathit{\boldsymbol{W}}_k} + {\theta _k}\left( {{\mathit{\boldsymbol{W}}_k} - {\mathit{\boldsymbol{W}}_{k - 1}}} \right), $ | (15) |
| $ {\mathit{\boldsymbol{W}}_{k - 1}} = {\rm{Pro}}{{\rm{x}}_{{\gamma _{k},g}}}\left( {{\mathit{\boldsymbol{Z}}_{k + 1}} - {\gamma _k}\nabla f\left( {{\mathit{\boldsymbol{Z}}_{k + 1}}} \right)} \right). $ | (16) |
式中:θk∈[0, 1)为外插值参数。一般会选择
实验采用中科院心理所征集的新浪微博用户数据,并通过在线填写大五人格问卷,通过筛选确定有效的问卷结果,然后选取新浪微博活跃用户,最终确定1 604名有效新浪微博用户数据。其中大五人格问卷采取的是目前国际上心理学界都认可的NEO大五人格问卷。筛选有效数据的方法是:首先过滤掉填写有规律的问卷以及全是一种选择的问卷,然后确定新浪微博活跃的用户,其活跃状态表现为用户的状态数大于50,在采集微博数据前3个月都发布过微博。
在得到1 604名新浪微博用户微博数据以及人格标签数据之后,首先要进行数据预处理。
微博数据特征的处理:
1) 将性别特征固定为0或1值;
2) 将用户昵称以及自我描述,计算其长度值;
3) 将所在地域信息,数值化,首先要制定一系列的数值对应,如北京对应001,天津对应002。
4) 将其他非数值类型转换为数值型,如是否认证,将ture转换为1,将false转化为0。
微博内容的处理:
5) 将所有微博内容为空、仅仅是超链接的微博、转发的微博以及图片、视频的微博内容过滤掉;
6) 提取微博文本信息特征,首先将同一个用户的所有微博整合在一起,然后通过中科院心理所的文心处理系统(http://ccpl.psych.ac.cn/textmind/)将文本内容提取出文本特征,包括第一人称单/复数代名词、第二人称单/复数代名词、第三人称单/复数代名词、情感词、正/负向情绪词、心理词汇、@数、表情数等102个维度。
最终确定994名被试者的微博数据及大五人格数据,其中391名男性,平均年龄24.6岁,分布在全国各地19省市。这994名新浪微博用户的大五人格得分分布情况如图 2所示。数据具有一定的代表性和真实性。
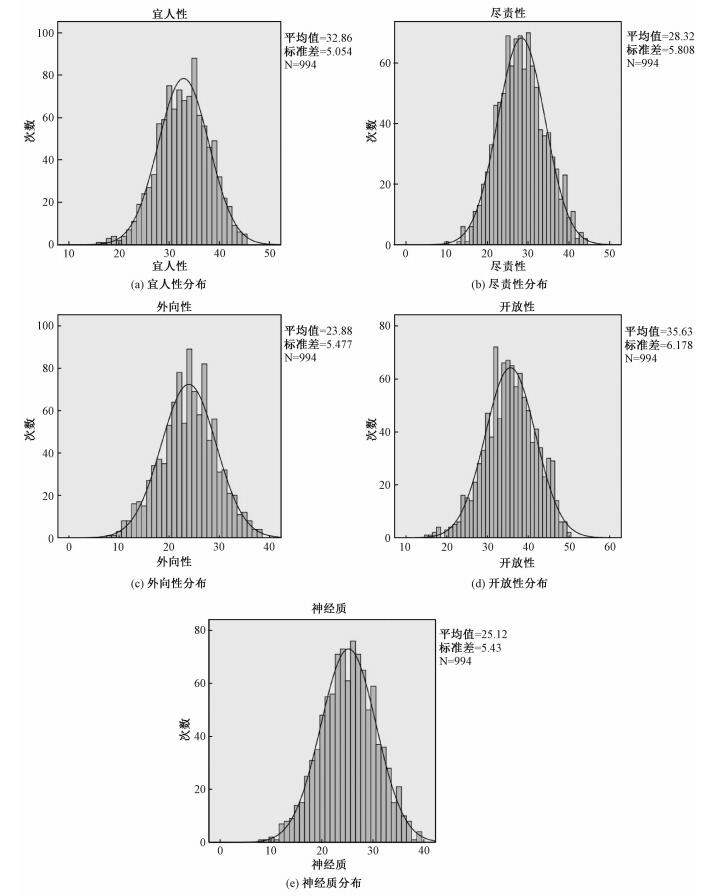
|
Download:
|
| 图 2 新浪微博用户大五人格得分分布图 Fig. 2 Big-Five personality score distributions of Sina Microblog users | |
本实验共挖掘新浪微博用户114个特征,包括静态特征、行为特征和文本特征3类,其中静态特征包括性别、地址、昵称、是否认证、自我描述等7类,行为特征包括发状态数、粉丝数、关注数、收藏数、互粉数等5类,文本特征包括发布的微博文本信息中提取出的102维特征。实验中,对994名新浪微博用户的114维微博特征和5维的人格特征进行相关性分析,分析结果如表 1所示。可以看出新浪微博用户的大五人格在社交网络中的表现以及与每种人格维度相关的数据特征。
|
|
表 1 新浪微博用户数据特征与大五人格相关系数 Table 1 Correlation coefficients between the data feature and Big-Five personality of Sina Microblog users |
神经质特质表现的是个体的情绪不稳定性,心理学上认为神经质得分高的个体常常表现为易烦恼、安全感差以及好自怜。神经质得分高的个体往往表现为缺乏责任感、偏内向、无情、怀疑心重且不易合作。该类个体上升为人格障碍时,表现为情绪不稳定和冲动控制缺乏,易发生暴力或恐吓行为,尤其在受到他人批评时。
新浪微博用户与神经质正相关的特征有:第三人称单数、自我描述长度、收藏数等,与神经质负相关的特征有互粉数。也就是说神经质得分较高的用户,在新浪微博中更多使用第三人称形式,喜欢收藏,同时自我描述的字数相对较多,而互粉数,即与其他用户互相关注的数目较少。
宜人性特质表现的是个体对他人的态度方面,心理学上认为宜人性得分高者,表现得信任他人,坦率真诚,关心他人,乐于助人,不具攻击性,谦逊,富有同情心。
新浪微博用户与宜人性正相关的特征有:积极情绪词,与宜人性负相关的特征有脏话。也就是说宜人性得分较高的用户更加倾向于使用积极的情绪词,如愉快、信任等等,而不喜欢说脏话。可以看出宜人性得分高的人比较乐观,友好和善。
外向性特质表现的是个体的人际关系方面,心理学上认为外向性得分高的个体常常表现为喜欢与人接触,热情、合群、有说服力、快节奏生活并且喜欢寻求刺激。
新浪微博用户与外向性正相关的特征有:粉丝数、收藏数、互粉数、第二人称复数、@数、惊叹、缩写、表情等等,与外向性负相关的特征有微博信息中英文单词比例。也就是说外向性得分较高的用户,关注他的以及互相关注的用户数目较多,喜欢收藏,多使用第二人称复数形式,喜欢引起好友的注意,缩写形式以及表情的使用较多,惊叹语气词使用较多。可见新浪微博外向性得分高的用户广交朋友,互动能力较强,善于传递正能量。
尽责性特质表现的是个体对自身各种情绪的控制能力,心理学上认为尽责性得分高的个体自信、高效、有条理、有很强的责任心、追求成功、不惧困难、逻辑性强、不易冲动。
新浪微博用户与尽责性正相关的特征有:分号、粉丝数等,与尽责性负相关的特征有收藏数。也就是说尽责性得分较高的用户,粉丝多,不喜欢收藏,在微博中,不喜欢使用分号形式。与尽责性强相关的特征较少,这也与尽责性个体自身的控制能力强相一致。
开放性特质表现的是个体的认知风格,心理学上认为神经质得分高的个体极富想象力、追求美、崇尚自然、敏感、喜欢尝试、求知欲强、不循规蹈矩。
新浪微博用户与开放性正相关的特征有:粉丝数、状态数、发表微博长度、第一人称单数、第三人称单复数、焦虑、情绪词等多种特征相关。也就是说开放性得分较高的用户粉丝多,发状态频率较高,微博内容的篇幅较长,倾向于使用第一人称和第三人称形式,并且更多地使用情绪词以及焦虑词进行表达。可见新浪微博开放性得分高的用户朋友多,交流多,谈论的话题涉及到各个方面,而且能够大方的表达自己的情绪,这与开放性人格特点是一致的。
3.3 实验结果使用获取的新浪微博用户人格标签数据以及微博数据集进行验证。将五种人格维度的预测作为五类任务,训练数据采用同样的数据集,也就是说数据样本为994,数据集维度为114,同时学习5种任务。采取本文引入的鲁棒多任务学习方法(RMTL),不基于任何假设的多任务学习框架,通过对预测模型使用混合结构范数进行建模,自动挖掘不同类别之间的内在关系,并识别出不相关任务,采用最小平方损失和与混合范数(核范数和L1/L2范数)进行建模。
实验中选取了4种经典的单任务学习方法,包括朴素贝叶斯(NB)、逻辑回归(LR)、随机森林(RF)以及RepTree算法进行对比,并且与使用最小平方损失和与Lasso范数进行计算建模的经典多任务学习方法(MTL)进行比较,采用5折交叉验证,从预测模型的准确率、精确率以及召回率进行了对比。
对数据集进行训练的过程中,通过随机分配训练数据与测试数据比例,最终当训练比为0.7的时候,模型效果最佳。并通过与其他5种经典的单任务学习方法以及传统多任务学习方法的对比,可以看出,对于小规模训练数据集的情况,采取鲁棒多任务学习方法(RMTL)预测结果优于传统的单任务学习算法。
同时将鲁棒的多任务学习与传统的基于所有任务都具有相关性假设的多任务进行对比,我们采用最小平方损失和与Lasso范数进行多任务计算建模[24],其模型为
| $ \begin{array}{l} W = \arg \mathop {\min }\limits_W L\left( {X,Y,W} \right) + \lambda \Omega \left( W \right)\\ = \arg \mathop {\min }\limits_W \sum\limits_{i = 1}^t {\left\| {W_i^T{X_i} - {Y_i}} \right\|_F^2} + \lambda {\left\| W \right\|_1}. \end{array} $ |
最终验证鲁棒的多任务学习模型性能优于Lasso范数建模的多任务学习模型。
鲁棒多任务学习算法主要包括2个重要的参数:ρ1和ρ2,前者用于控制组结构的低秩约束,后者是控制组稀疏约束,针对任务聚类和异常任务同时存在的情况设计。在实验过程中,经过训练得到正则化参数,当ρ1=400,ρ2=-20的时候,模型效果最佳,预测准确率最高。
图 3是几种方法的正确率、精确率和召回率的图形结果。这是基于新浪微博用户的数据,在提取出相同的特征基础上,进行训练的结果。可以看出在正确率、精确率以及召回率上,本文提出的基于鲁棒多任务学习预测新浪微博用户的大五人格方法优于其他几种方法。鲁棒多任务学习方法有效利用5种任务之间的关联信息,同时避免不相关信息带来的干扰,在训练数据样本小的环境下,提高了模型的预测性能。
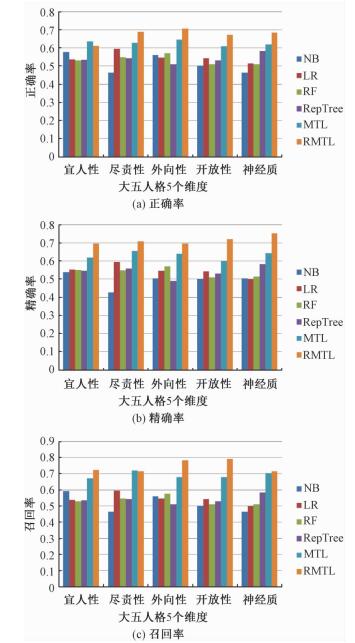
|
Download:
|
| 图 3 6种方法比较 Fig. 3 Comparison among the six methods | |
社交网络用户的人格数据获取非常困难,实验中,基于994名新浪微博用户的大五人格数据,提取出微博的静态数据、动态数据以及文本数据,共114维特征。在训练样本数量少,维度低的情况下,使用传统的单任务学习方法,极易会造成结果过拟合现象,因此泛化性能不高。同时由于5种任务之间存在着一定的相关性,而传统的单任务学习方法并没有充分利用其关联信息。多任务学习方法正好弥补了这两个缺陷。但是多任务学习是基于多个任务之间都存在相关这样很强的假设前提的,而5类人格预测任务之间并不都是存在着很强的相关性,因此使用一般的多任务学习在并行学习5个维度的人格预测任务过程中,由于不能识别存在的异常任务,造成预测结果不佳。所以使用鲁棒的多任务学习方法对新浪微博用户进行大五人格预测,取得了较高的结果,既能有效利用任务之间的相关信息,又能识别出异常任务,因此提高了模型的泛化性能。
4 结束语随着社交网络在现实生活中的盛行,并且由于社交网络中用户行为数据的便于记录、获取、存储与分析,因此将人格理论与社交网络相结合的研究也越来越受到研究者的重视。但是这一方面的研究仅仅出于初步阶段,大部分还都是采用单任务建模的方法,忽略了多个任务之间的潜在联系,因此本文,提出了采用多任务学习的思路预测社交媒体用户的人格变量,并通过真实的新浪微博用户的数据进行了验证,同时通过在相同数据集上采取传统的单任务学习方法进行比较,实验证明多任务学习方法的预测效果更优于传统单任务方法,也优于传统的假设所有任务都相关的多任务学习方法。
社交网络预测用户人格研究还存在很大的研究空间,不同的社交网络数据结构的不同,造成了预测模型的差异,可以在建模过程中合理利用多任务之间的共享信息,并且在数据特征提取方面还需要更进一步的研究,本实验也将会继续扩大实验规模,采集更多的社交网站用户数据,比如采集微博的动态数据,也就是一些随着时间变化的数据特征,并且考虑提取视频和图片信息,同时考虑更多的多任务学习方法,修改预测模型,更大幅度地提高预测模型精度及泛化性能。
| [1] |
Goldberg L R, Johnson J A, Eber H W, et al. The international personality item pool and future of public-domain personality measures[J]. Journal of Research in Personality, 2006, 40(1):84–96.
DOI:10.1016/j.jrp.2005.08.007 |
| [2] |
Ortigosa A, Carro R M, Quiroga J I. Predicting user personality by mining social interactions in Facebook[J]. Journal of Computer and System Sciences, 2013, 80(1):57–71.
|
| [3] |
Wald R, Khoshgoftaar T M, Napolitano A, et al. Using Twitter content to predict psychopathy[C]//Proceedings of the 201211th International Conference(ICMLA) on Machine Learning and Applications. USA, 2012: 394-401.
http://ieeexplore.ieee.org/document/6406768/ |
| [4] |
Li L, Li A, Hao B, et al. Predicting active users' personality based on micro-blogging behaviors[J]. Plos One, 2014, 9(1):e84997.
DOI:10.1371/journal.pone.0084997 |
| [5] |
Wald R, Khoshgoftaar T M, Sumner C. Machine prediction of personality from Facebook profiles[C]//Proceedings of the 2012 IEEE 13rd International Conference on Information Reuse and Integration. LasVegas, USA, 2012: 109-115.
http://ieeexplore.ieee.org/document/6302998/ |
| [6] |
Bachrach Y, Kosinski M, Graepel T, et al. Personality and patterns of Facebook usage[C]//Proceedings of the 3rd Annual ACM Web Science Conference. New York, USA, 2012: 24-32.
|
| [7] |
Iacobelli F, Gill A J, Nowson S, et al. Large scale personality classification of bloggers[C]//Fourth International Conference on Affective Computing & Intelligent Interaction. Memphis, USA, 2011: 568-577.
https://dl.acm.org/citation.cfm?id=2062928 |
| [8] |
Nowson S, Oberlander J. Identifying more bloggers: towards large scale personality classification of personal[C]//International Conference on Weblogs and Social. Colorado, USA, 2007: 1-7.
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.64.2021 |
| [9] |
Caruana R. Multitask learning[J]. Machine Learning, 1997, 28(1):41–75.
DOI:10.1023/A:1007379606734 |
| [10] |
Argyriou A, Evgeniou T, Pontil M. Convex multi-task feature learning[J]. Machine Learning, 2008, 73(3):243–272.
DOI:10.1007/s10994-007-5040-8 |
| [11] |
Ben-David S, Schuller-Borbely R. A notion of task relatedness yielding provable multiple-task learning guarantees[J]. Machine Learning, 2008, 73(3):273–287.
DOI:10.1007/s10994-007-5043-5 |
| [12] |
Zhang Y, Yeung D Y. Multi-task learning using generalized t process[J]. Journal of Machine Learning Research Proceedings Track, 2010, 9(1):964–971.
|
| [13] |
Charuvaka A, Rangwala H. Classifying protein sequences using regularized multi-task learning[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2014, 11(6):1087–1098.
DOI:10.1109/TCBB.2014.2338303 |
| [14] |
Zhang J, Ghahramani Z, Yang Y. Learning multiple related tasks latent independent component analysis[J]. Advances in Neural Information Systems, 2006, 18:1585–1592.
|
| [15] |
Olshausen B A, Field D J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images[J]. Nature, 1996, 381(6583):607–609.
DOI:10.1038/381607a0 |
| [16] |
Mao X, Wu O, Hu W, et al. Nonlinear Classification via linear SVMs and multi-task learning[C]//International Conference on Conference on Information & Knowledge Management. Shanghai, China, 2014: 1955-1958.
|
| [17] |
白朔天, 袁莎, 程莉, 等. 多任务回归在社交媒体挖掘中的应用[J]. 哈尔滨工业大学学报, 2014, 46(9):100–110.
|
| [18] |
Evgeniou T, Pontil M. Regularized multi-task learning[C]//Proceedings of Knowledge Discovery and Data Mining. Washington, USA, 2004: 109-117.
|
| [19] |
Yu S, Tresp V, Yu K. Robust Multi-task Learning with t-Processes[C]//Proceedings of the 24th International Conference on Machine learning. Madison, USA, 2007: 1103-1110.
|
| [20] |
Chen J, Zhou J, Ye J. Integrating low-rank and group-sparse structures for robust multi-task learning[C]//Proceedings of the 10th ACM SIGKDD international conference on Knowledge discovery and data mining. California, USA, 2011: 42-50.
https://scholars.opb.msu.edu/en/publications/integrating-low-rank-and-group-sparse-structures-for-robust-multi |
| [21] |
Xu H, Leng C. Robust multi-task regression with grossly corrupted observations[C]//Proceedings of the 15th International Conference on Artificial Intelligence and Statistics (AISTATS). La Palma, Canary Islands, 2012: 1341-1349.
|
| [22] |
Gong P, Ye J, Zhang C. Robust multi-task feature learning[C]//Knowledge Discovery and Data Mining International Conference'12. Beijing, China, 2012(8): 895-903.
|
| [23] |
Tibshirani R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, 2011, 73(3):273–282.
DOI:10.1111/rssb.2011.73.issue-3 |
| [24] |
Ji S, Ye J. An accelerate gradient method for trace norm minimization[C]//Proceedings of the 26th Annual International Conference on Machine Learning. Montreal, Canada, 2009: 457-464.
|
 2018, Vol. 35
2018, Vol. 35 


