支持向量机作为一个经典的分类方法,在20世纪90年代中期由Cortes和Vapnik[1]在统计学习理论的基础上提出。支持向量机具有很强的泛化能力,能较好地解决局部极小、过学习和维数灾难等传统机器学习方法中存在的问题[2]。尽管在很多方面,支持向量机都具有其他学习方法不可比拟的优势,但是它也存在局限性,例如抗躁性差[3]、对不平衡数据分类敏感[4]等。传统支持向量机等同地对待所有训练样本点,并赋予它们相同的权值,但是真实数据中经常含有噪点,不同的训练样本点对分类面的作用也是不同的,如若不将重要训练样本与噪点区分开来,则最终得到的分类面也往往不是真正的最优分类面,出现“过学习”现象。针对这种情况,研究者提出模糊支持向量机(FSVM)[5-7],根据不同训练样本对分类面的作用,赋予其不同的模糊隶属度(即权值),分配给重要样本更大的隶属度值,分配给噪点很小的隶属度值,以减少它们对分类结果的影响,增加算法的抗噪能力。
虽然模糊支持向量机降低了噪点对分类结果的影响,很好地提高了分类器的性能,但其对于不平衡数据分类问题依然敏感。当数据不平衡时,支持向量机的分类效果不佳,容易将绝大多数的少数类分类为多数类,导致少数类的分类精度很低。然而,在许多实际应用中,相比于多数类,少数类提供的信息往往更加重要,比如在医疗检测,如果将一个病人检测为健康人,从而耽误了病人的就医时间,则会导致非常严重的后果。因此,少数类的分类精度低是很不理想的结果。为解决这一问题,国内外学者进行了大量研究。其中,欠采样[8]就是一种解决不平衡数据分类问题的有效方法。然而,常用的随机欠采样方法由于其自身的随机性和盲目性,容易造成重要样本信息的丢失,影响分类效果,且分类稳定性较差。
针对支持向量机在不平衡数据集上分类效果不理想和算法容易受训练数据集中的噪声影响等问题,本文提出一种基于类重叠度欠采样的不平衡模糊多类支持向量机。首先通过LOF局部离群点因子[9]和箱线图[10]的方法删除训练数据集中的噪声样本,然后设置合适的采样数目,根据改进的类重叠度对去除噪声样本后的数据集欠采样,抽取对分类起关键作用的支持向量,最大限度地维持原有的数据分布信息,并且降低数据集的不平衡比例,最后将代表每个样本点重要程度的类重叠度作为隶属度值,构造模糊多类支持向量机。实验结果表明,该算法能够在保证良好的分类精度的同时,缩减运行时间,且其克服了随机欠采样方法容易丢失重要样本信息和分类结果不稳定的缺点。
1 基于重采样的不平衡数据学习方法目前,针对不平衡数据分类的方法可以分为数据、算法两个层面。算法层面主要是对已有算法进行改进,提升算法对少数类的准确识别率,如集成学习方法、代价敏感算法等。数据层面主要是通过重采样技术,重新构造训练数据集,从而降低数据集的不平衡度。
重采样技术主要分为过采样技术和欠采样技术。过采样技术通过一定的方法增加少数类的样本数目,其中比较常用的是随机过采样方法和SMOTE方法[11]。由于新添许多样本,过采样技术容易造成数据冗余和分类器过拟合的现象。欠采样技术采用某种规则舍弃部分多数类样本,使得多数类样本数目趋近于少数类样本数目。最常用的方法是随机欠采样[12]及其改进的欠采样方法,如Kubat和Matwin[13]的单边选择方法,谢纪刚和裘正定[14]提出的加权Fisher线性判别方法。欠样技术由于删除了部分多数类样本,可能导致分类时数据信息的缺失,从而对分类结果造成一定的影响。
数据重采样技术的关键在于采用什么样的采样方法,能够最大限度地保留原数据集的分布信息,得到具有代表性、对分类起关键作用的样本集。本文提出一种基于类重叠度的欠采样技术,抽取对分类起决定性作用的支持向量,较好地维持了原有的数据分布,在保证良好的分类精度的基础上,减小算法的运行时间。
2 基于LOF去噪和类重叠度欠采样的非平衡数据预处理算法 2.1 算法思想在支持向量机的分类中,并不是所有的样本都起着相同的作用,支持向量机算法的最终分类精度是由样本集中的支持向量决定的。支持向量在整个训练样本集中所占的比例非常小,在支持向量机的训练过程中,花费大量的时间去训练非支持向量的样本,将大大增加算法的运行成本。鉴于支持向量机最终是由支持向量决定的,在数据预处理的过程中,从训练样本集中抽取出支持向量,删除非支持向量的样本,对最终的算法模型并不会造成影响,如此可以从样本集中删除大量的无用样本,只余重要样本,提高算法运行效率的同时,降低训练数据集的不平衡比例。
由于支持向量机模型的以上特点,且支持向量分布在分类决策面附近,即各类的类重叠区域,类重叠度越高的训练样本,成为支持向量的可能性越大,本节通过对训练数据集进行预处理,采用LOF和箱线图的方法首先去除数据集中的噪声样本,然后基于类重叠度的思想,选择性地对训练样本集进行欠采样,保留对分类起决定性作用的支持向量,删除对分类没有作用的非支持向量的样本。具体为:计算每个训练样本的类重叠度,并将训练样本集根据类重叠度从大到小的顺序排列,设置抽取的样本数,抽取类重叠度大的部分样本集作为新的训练样本集。较之于原数据集,新的训练数据集在数据规模上大大减小,且数据集的不平衡比例也有所降低。
2.2 基于LOF和箱线图的去噪方法支持向量机在训练过程中平等地对待所有训练样本,算法很容易受到噪声样本的干扰,使得分类结果产生偏差。在不平衡数据分类中,虽然在数据预处理的过程中,对数据集欠采样能够抑制不平衡数据对分类的影响,但支持向量机仍然会受到噪声样本的干扰。所以,在对不平衡数据集欠采样处理前,首先应该去除数据集中的噪声样本。本节采用LOF局部离群点因子[9]和箱线图[10]去除噪声样本。
LOF局部离群点因子表示数据对象的离群程度,数据对象的LOF局部离群点因子越大,则该数据对象的离群程度越高,越有可能是噪声样本。基于此思想,可以计算出每个训练样本点的局部离群点因子LOF,然后采用箱线图的方法,剔除训练数据集中LOF过大的一些样本。
箱线图方法中,超过内栏的值被认为是潜在的异常值,代表相对稀有的样本点。为了去除数据集中的噪声样本,结合局部离群点因子LOF的特性,通过对训练数据集的局部离群点因子作箱线图,剔除离群点因子超过箱线图的上内栏的部分样本集,这些样本的离群点因子过大,是噪声样本的可能性很大。
综上,本节提出一种基于LOF和箱线图的去噪算法,算法如表 1所示。
|
|
表 1 基于LOF和箱线图的去噪算法 Table 1 Denoising algorithm based on LOF and box-whisker plot |
欠采样方法容易删除重要的数据样本,造成分类结果的偏差,而对于支持向量机而言,其最终的分类精度是由训练数据集中的支持向量决定的,所以如何抽取训练数据集中的支持向量是基于支持向量机的欠采样方法的关键。支持向量分布在分类决策面附近,即各类的类重叠区域,类重叠度越高的训练样本,成为支持向量的可能性越大,它的重要程度也越高。基于此,本文根据各训练样本点的类重叠度,选择性地对训练数据集进行欠采样,保留对分类起决定性作用的支持向量,删除对分类没有作用的训练样本。
文献[15]定义类(Cp, Cq)在数据点xi处的重叠度:
| $ \begin{gathered} {\mu _2}\left( {{x_i}, {C_p}, {C_q}} \right) = {\text{Min}}\left\{ {\frac{{\left\| {{x_i}-{V_p}} \right\|}}{{\left\| {{x_i}-{V_p}} \right\| + \left\| {{x_i}-{V_q}} \right\|}}, } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{\left\| {{x_i} - {V_q}} \right\|}}{{\left\| {{x_i} - {V_p}} \right\| + \left\| {{x_i} - {V_q}} \right\|}}} \right\}, \hfill \\ \end{gathered} $ | (1) |
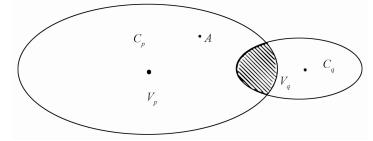
式中:Vp和Vq分别是类Cp和Cq的类中心点;||xi-Vp||和||xi-Vq||分别表示xi到两类中心点的距离;μ2(xi, Cp, Cq)表示xi属于类Cp和类Cq的模糊度。类Cp和类Cq的划分越清楚,重叠度越低,其值分布在0~0.5。然而,该方法只适用于均衡分布的数据集,对于分布不均衡的数据集,它存在不足。由图 1可以看出A点距两类中心点的距离相等,按照类重叠度公式1,A点计算得到的的类重叠度为0.5,为最高的类重叠度,这显然不符合实际情况,从图 1可以明显看到,A点并不在两类的重叠区域。
|
Download:
|
| 图 1 类重叠度图 Fig. 1 Class overlap | |
基于上述观察,本文改进类重叠度公式为
| $ \begin{gathered} {\mu _2}\left( {{x_i}, {C_p}, {C_q}} \right) = {\text{Min}}\left\{ {\frac{{\left\| {{x_i}-{V_p}} \right\|/{R_p}}}{{\left\| {{x_i}-{V_p}} \right\|/{R_p} + \left\| {{x_i}-{V_q}} \right\|/{R_q}}}, } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{\left\| {{x_i} - {V_q}} \right\|/{R_q}}}{{\left\| {{x_i} - {V_p}} \right\|/{R_p} + \left\| {{x_i} - {V_q}} \right\|/{R_q}}}} \right\}, \hfill \\ \end{gathered} $ | (2) |
式中:Rp和Rq分别是类Cp和类Cq的平均类中心距离,计算公式为
对于多分类的情况,定义每个训练样本点的类重叠度为该点所属类分别与其他各类在该点的类重叠度的均值。假设训练样本有k个类,分别是C1, C2, …, Ck,样本点xi属于其中一个类Cp,定义xi的k类重叠度为xi的所属类Cp分别与其他各类在xi处的二类重叠度的均值,即
| $ {\mu _k}\left( {{x_i}} \right) = \frac{1}{{k-1}}\sum\limits_{q \ne p} {{\mu _2}\left( {{x_i}, {C_p}, {C_q}} \right)} . $ | (3) |
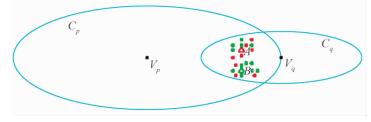
然而,式(3)仍存在一定局限性,如图 2所示,A点属于类Cp,用红色的三角形表示,B点属于类Cq,用绿色的三角形表示,它们都处于两类的重叠区域中,且它们与两类的类中心距离分别相等。如果按照式(3)计算,类Cp和类Cq在A点和B点的类重叠度相等。但是由图 2可以看出:A点的10个最近邻点中有5个属于自己类,另5个属于类Cq;B点的10个最近邻点中却有7个都是属于自己类,只有3个属于类Cp,容易得到类Cp和类Cq在A点的类重叠度应比B点更大。由此,启发我们可以用训练样本点的K个近邻样本中异类样本所占的比例来反映该点的类重叠度。所以,对于k类分类,进一步改进类重叠度公式为
|
Download:
|
| 图 2 不同点的类重叠度 Fig. 2 Class overlap for different points | |
| $ {\mu _k}\left( {{x_i}} \right) = 0.5 \times \left( {\frac{1}{{k-1}}\sum\limits_{q \ne p} {{\mu _2}\left( {{x_i}, {C_p}, {C_q}} \right) + \frac{{{K_i}}}{K}} } \right), $ | (4) |
式中:K表示K个近邻样本点;Ki表示第i个样本点的K个近邻样本中异类样本数。
综上,本节基于LOF去噪和类重叠度欠采样的非平衡数据预处理的算法,具体描述如表 2所示。
|
|
表 2 基于LOF去噪和类重叠度欠采样的非平衡数据预处理算法 Table 2 Imbalanced data preprocessing algorithm based on LOF denoising method and class-overlap degree undersampling method |
传统的支持向量机等同地对待所有的训练样本点,对所有错分的训练样本点分配相同的权重。然而,在实际应用中,数据集中的不同样本点对分类产生的作用是不同的,因此一个合理的做法是根据各训练样本点的重要性,为每个训练样本点分配不同的权值。第2节提出的基于LOF去噪和类重叠度欠采样的预处理算法,可以有效地删除噪声样本和冗余样本,保留支持向量,数据集的不平衡比例也明显降低。预处理过后的数据集中每个样本点的类重叠度代表着该样本点的重要程度,以相应的类重叠度作为隶属度值,构造模糊多类支持向量机。
对于k类分类,给定一个带有类别标记以及模糊隶属度的训练样本集S={(xi, yi, ui), i=1, 2, …, N}。式中:xi∈Rn是训练样本集;yi∈{1, 2, …, k}是对应的类别标记;ui=μk(xi)为第i个样本的改进后的类重叠度,见公式(4)。则基于LOF去噪和类重叠度欠采样的不平衡模糊多类支持向量机模型如下(以Crammer-Singers直接多分类算法[16]为基础模型)
| $ \min \frac{1}{N}\sum\limits_{i = 1}^N {{u_i}{\varepsilon _i}} + \frac{\lambda }{2}\sum\limits_{i = 1}^k {\mathit{\boldsymbol{w}}_i^{\text{T}}{\mathit{\boldsymbol{w}}_i}}, $ | (5) |
| $ \begin{gathered} {\text{subject}}\;{\text{to}} \hfill \\ \mathit{\boldsymbol{w}}_{{y_i}}^{\text{T}}{x_i}-\mathit{\boldsymbol{w}}_j^{\text{T}}{x_i} \geqslant 1-{\varepsilon _i}, \left( {i = 1, \cdots, N, j \ne {y_i}} \right) \hfill \\ {\varepsilon _i} \geqslant 0, \left( {i = 1, \cdots, N} \right) \hfill \\ {\mathit{\boldsymbol{w}}_i} \in {{\bf{R}}^{n + 1}}, \left( {i = 1, \cdots, k} \right). \hfill \\ \end{gathered} $ |
式中:λ>0是一个调节因子,类似于标准支持向量机中的参数C;ε=[ε1, ε2, …, εN]表示松弛变量。
由式(5)可以看出,每个样本点xi的错分代价为uiεi,模糊隶属度ui越小,则损失参数εi对目标函数值的影响越小,所对应的样本点xi越不重要。
综上,基于LOF去噪和类重叠度欠采样的不平衡模糊多类支持向量机的具体算法描述,如表 3所示。
|
|
表 3 基于LOF去噪和类重叠度欠采样的不平衡模糊多类支持向量机算法 Table 3 Imbalanced fuzzy multiclass support vector machine algorithm based on LOF denoising method and class-overlap degree undersampling |
为了验证本文方法的有效性和普适性,本节实验由模拟数据实验和实际数据实验两部分组成。实验在2.4 GHz/8 GB的PC主机上利用Matlab R2015软件实现,所有数值实验以Crammer-Singers直接多分类支持向量机作为基础模型。
4.1 模拟数据实验为了验证基于LOF去噪和类重叠度欠采样的不平衡数据预处理算法的有效性,本节将在一个不平衡的模拟数据集上进行实验,并根据模拟实验结果,分析上述预处理算法的有效性。
随机生成3类正态分布的数据集,其中类1为均值为[2, 2],方差为[0.2, 0;0, 0.3]的样本集,共50个样本点;类2为均值为[3.5, 2],方差为[0.3, 0;0, 0.4]的样本集,共100个样本点;类3为均值为[2.8, 3.8],方差为[0.4, 0;0, 0.5]的样本集,共200个样本点。为了验证提出的预处理算法的去噪能力以及更符合实际应用情况,在[0, 5]×[0, 6]范围内随机产生50个噪声样本。加上噪声样本,总的模拟数据集共400个样本。设置预抽取的样本数为200。
对以上含噪声的模拟数据,进行基于LOF去噪和类重叠度欠采样的不平衡数据预处理,结果如图 3所示。为方便区别,在下面所有图中,类1中的样本由“*”表示,类2中的样本由“+”表示,类3中的样本由“o”表示,噪声样本由“Δ”表示。
|
Download:
|
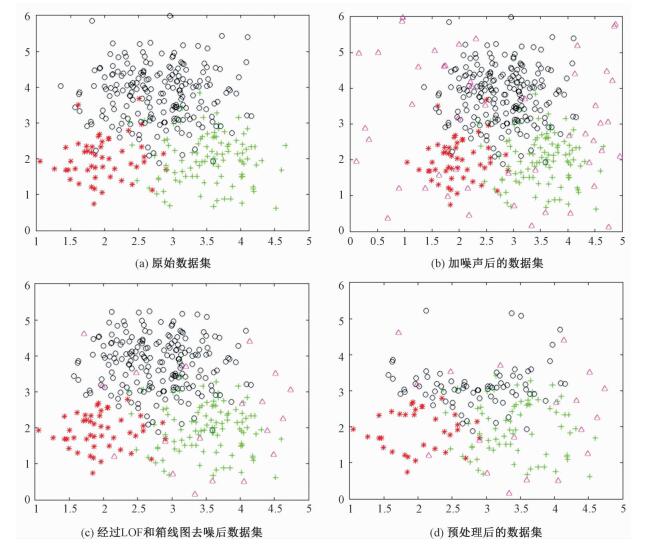
| 图 3 非平衡数据预处理算法的模拟实验结果 Fig. 3 Simulation results of imbalanced data preprocessing algorithm | |
图 3为上述非平衡数据预处理算法在加噪后的3类正态分布的数据集上的分段处理效果图。图 3(a)显示原有的正态分布的数据集,共350个样本点。图 3(b)是在原有数据集中增加50个噪声样本后的数据集分布,可以看出,增加噪声样本后的数据集的分布比较复杂,如果直接以这样的数据集进行分类,将严重影响分类结果。图 3(c)是经过LOF和箱线图去除噪声样本后的数据集,剔除42个噪声样本,剩余358个样本点,由图可以看出,经过去噪后的数据集,噪声样本明显减少,数据集分布较为明晰。图 3(d)是在去噪后的数据集中基于类重叠度由大到小的顺序抽取的200个数据集,即预处理过后的数据集,由图可以看出,样本数量明显减少,但是缩减过后的数据集依然较好地保留了原有的数据分布,尤其在分类决策面附近对分类起着关键作用的支持向量得到了比较好的保留,且数据集的不平衡比例经过欠采样后也明显地降低,由1:2:4降低至1:2.30:2.76,剔除了多数类中的大量冗余样本。
4.2 实际数据实验1) 评价准则
对于不平衡数据分类问题,常用的评价指标有AvgAcc,G-mean[17]等。假设k类分类,Acci表示第i类的分类精度,则AvgAcc是各类分类精度的算术平均值,G-mean是各类分类精度的几何平均值,计算方法如下:
| $ \begin{gathered} {\text{AvgAcc = }}\frac{1}{k}\sum\limits_{i = 1}^k {{\text{Ac}}{{\text{c}}_i}}, \hfill \\ {\text{G-mean}} = {\left( {\prod\limits_{i = 1}^k {{\text{Ac}}{{\text{c}}_i}} } \right)^{\frac{1}{k}}}. \hfill \\ \end{gathered} $ |
2) 实验数据
本次实验选用UCI数据库中4个UCI数据集,数据集具体参数见表 4,其中不平衡率为各类别的样本数量与最小类的样本数量的不平衡比例。
|
|
表 4 UCI数据集及相关属性 Table 4 UCI datasets and related attributes |
实验中,除User数据集自带训练集和测试集,其他每个数据采用5折交叉检验,并取5次结果的均值作为最终结果。由于Ecoli和Glass数据集中某些类的样本数量较少,并不适用于5折交叉检验,所以实验将Ecoli中原样本数量分别为2, 2, 5, 20的4类合并为一类,将Glass中原样本数量分别为9, 13, 17的3类合并为一类。
3) 实验结果与分析
为验证本文方法的有效性和普适性,将本文算法与原支持向量机、常用于不平衡数据分类的DEC[18]算法、用于不平衡数据分类的模糊支持向量机FSVM-CLLexpcen[19]和随机欠采样的支持向量机进行比较。实验采用5折交叉验证方法所得的均值作为最终实验结果,所有实验的测试集和训练集都相同。其中,因为随机采样的支持向量机具有采样的随机性的特点,为了更公平地展示它的分类效果,其实验采用5次5折交叉验证的均值作为最终结果。实验中支持向量机算法中的参数λ的取值范围是{10-5, 10-4, …, 105}。
实验结果如表 5、表 6所示,表 5显示算法中每个数据集的实际样本数和算法预抽取的样本数,表 6列出各方法在不平衡数据集上分类精度和运行时间的比较结果。其中,CMSVMsuiji表示随机欠采样的支持向量机。
|
|
表 5 实验中各数据集抽取样本数 Table 5 Number of samples extracted from each dataset in the experiment |
|
|
表 6 实验结果 Table 6 Experimental results |
表 5显示,抽取的样本集只占原数据集的一小部分。由表 6的实验结果可以看出,就运行时间而言,由于训练样本数的减少,本文算法和随机欠采样支持向量机在运行时间上要小于其他算法。此外,因为本文算法需要计算每个样本点的LOF局部离群点因子和类重叠度,所以在运行时间上会略高于随机欠采样的支持向量机。比如在Balance数据集上,本文方法运行时间是105 s,随机欠采样的支持向量机的运行时间是42 s, 但其他方法的最少运行时间是112 s,本文方法的运行时间要高于随机欠采样的支持向量机的运行时间,但要低于其他方法的运行时间。就分类精度而言,除在Glass数据集上,本文算法的精度以微小的差距低于一些算法,其他数据集上,本文算法的分类精度均要优于其他算法。如在Balance数据集中,就AvgAcc评价准则,本文方法的分类精度为0.87,其他方法的最高分类精度为0.85,本文方法要高于其他方法,就G-mean评价准则,本文方法的分类精度为0.85,其他方法的最高分类精度为0.72,本文方法要高于其他方法。就实验结果的稳定性而言,同样是抽取相同数目的训练样本,本文算法是根据训练数据集的类重叠度由大至小抽取样本集,实验结果是固定的,然而对于随机欠采样的支持向量机,由于每次随机采样的训练样本集可能不同,实验结果也不稳定。综上,对于相同的数据集,本文提出的算法在运行时间上仅次于随机欠采样支持向量机;在分类精度上要高于其他算法;而且本文算法还克服了随机欠采样的支持向量机的实验结果不稳定的缺点。
5 结论针对支持向量机在不平衡数据集上分类效果并不理想且对噪声数据敏感的问题,本文提出基于类重叠度欠采样的不平衡模糊多类支持向量机算法,首先对数据集进行预处理,采用LOF局部离群点因子和箱线图结合的方法删除训练数据集中的噪声样本,然后设置合适的采样数目,根据类重叠度抽取对分类起关键作用的支持向量。预处理过后的数据集最大限度地维持了原有的数据分布信息,并且降低了原数据集的不平衡比例。算法最后将代表每个样本点的重要程度的类重叠度作为隶属度值,构造模糊多类支持向量机。由于算法是基于类重叠度对训练数据集进行欠采样,支持向量等重要样本被较好地保留下来,且只要设定固定的抽样数目,则实验结果便是固定的,所以该算法克服了随机欠采样方法容易丢失重要样本信息和实验结果不稳定的缺点。实验结果表明,该算法在能够很好地提升支持向量机在不平衡且含噪声的数据集上的分类精度的同时,缩减算法的运行时间。
| [1] |
Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3):273–297.
|
| [2] |
康健, 左宪章, 唐力伟, 等. 基于灰色支持向量机的裂纹扩展信息预测研究[J]. 机械强度, 2010, 32(5):120–123.
|
| [3] |
Cao L J, Lee H P, Chong W K. Modified support vector novelty detector using training data with outliers[J]. Pattern Recognition Letters, 2003, 24(14):2479–2487.
DOI:10.1016/S0167-8655(03)00093-X |
| [4] |
Wang B X, Japkowicz N. Boosting support vector machines for imbalanced data sets[J]. Knowledge and Information Systems, 2010, 25(1):1–20.
|
| [5] |
Lin C F, Wang S D. Fuzzy support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2):464–471.
DOI:10.1109/72.991432 |
| [6] |
Huang H P, Liu Y H. Fuzzy support vector machine for pattern recognition and data mining[J]. International Journal of Fuzzy Systems, 2002, 4(3):826–835.
|
| [7] |
Jiang X, Yi Z, Lü J C. Fuzzy SVM with a new fuzzy membership function[J]. Neural Computing & Applications, 2006, 15(3):268–276.
|
| [8] |
Castillo B, Gennaro S D, Monaco S, et al. On regulation under sampling[J]. IEEE Transactions on Automatic Control, 1997, 42(6):864–868.
DOI:10.1109/9.587345 |
| [9] |
韩家炜. 数据挖掘:概念与技术[M]. 北京: 机械工业出版社, 2012: 1-3.
|
| [10] |
McClave J Y, Benson P G, Sincich T. 商务与经济统计学[M]. 易丹辉, 李扬, 译. 北京: 中国人民大学出版社, 2014: 67-69.
|
| [11] |
Chawla N V, Bowyer K W, Hall L O, et al. SMOTE:synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2011, 16(1):321–357.
|
| [12] |
Chen L, Bao L, Li J, et al. An aliasing artifacts reducing approach with random undersampling for spatiotemporally encoded single-shot MRI[J]. Journal of Magnetic Resonance, 2013, 237(6):115–124.
|
| [13] |
Kubat M, Matwin S. Addressing the curse of imbalanced training sets: one-sided selection[C]//Fisher D H. 14th International Conference on Machine Learning. San Francisco: MorganKaufmann Press, 1997: 179-186.
|
| [14] |
谢纪刚, 裘正定. 非平衡数据集Fisher线性判别模型[J]. 北京交通大学学报, 2006, 30(5):15–18.
|
| [15] |
瞿俊, 姜青山, 翁芳菲. 基于重叠度的层次聚类算法[J]. 计算机研究与发展, 2007, 44(s2):181–186.
|
| [16] |
Crammer K, Singer Y. On the algorithmic implementation of multiclass kernel-based vector machines[J]. Journal of Machine Learning Research, 2001, 2(2):265–292.
|
| [17] |
浮盼盼. 大规模不均衡数据分类方法研究[D]. 大连: 辽宁师范大学, 2014.
http://www.docin.com/p-981415390.html |
| [18] |
Veropoulos K, Campbell C, Cristianini N. Controlling the sensitivity of support vector machines[C]//International Joint Conference on Artificial Intelligence. Stockholm: IJCAI Press, 1999: 55-60.
|
| [19] |
Batuwita R, Palade V. FSVM-CIL:fuzzy support vector machines for class imbalance learning[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(3):558–571.
DOI:10.1109/TFUZZ.2010.2042721 |
 2018, Vol. 35
2018, Vol. 35 


