2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
外辐射源雷达是利用第三方发射的电磁信号实现目标探测和跟踪的雷达,结构与双基连续波雷达相像。随着数字电视信号的普及和发展,外辐射源雷达越来越凸显出优势。该体制雷达采用相干处理技术,需要参考信号作匹配滤波。而实际工作环境通常比较复杂,参考通道中多径杂波将引起信杂噪比下降,增加虚警,降低目标检测性能[1-2]。因此参考通道多径杂波抑制成为关键问题之一。
对于多径杂波的抑制问题,已经有许多有效算法,诸如时域[3-4]、空域[5]等滤波方法,以及信号重构算法[6]。实际工作中,空域滤波对参考天线尺寸、阵元数目等有较高要求,而信号重构算法虽然能取得良好效果,但工作量较大。为此,本文据数字电视信号自相关函数特征,提出k-前向预测滤波算法。该算法是一种时域自参照的滤波算法,运算量小,多径杂波抑制效果较为明显。该算法单元也可级联在阵列天线做DBF之后,解决空域滤波杂波抑制不理想的问题。
1 多径杂波强度和影响分析 1.1 多径杂波强度参考信号通常包含来自发射塔的直达波信号以及地物反射产生的大量多径杂波。直达波信号为需要提取的有用信号。下面假定收发站间距40 km时,分析参考信号中多径杂波功率Pr和直达波的功率Pd比。根据已知有[7]
| $ {P_{\rm{d}}} = \frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{\rm{r}}}{\lambda ^2}}}{{{{\left( {4{\rm{ \mathsf{ π} }}} \right)}^2}{R^2}}}, $ | (1) |
| $ {P_{\rm{r}}} = \sum\limits_{i = 1}^N {{P_{{\rm{r}}i}}} = \frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{\rm{r}}}{\lambda ^2}}}{{{{\left( {4{\rm{ \mathsf{ π} }}} \right)}^3}}}\left( {\sum\limits_{i = 1}^N {\frac{{M{\sigma _i}}}{{R_{1i}^2R_{2i}^2}}} } \right), $ | (2) |
| $ \frac{{{P_{\rm{r}}}}}{{{P_{\rm{d}}}}} = \frac{{{R^2}}}{{4{\rm{ \mathsf{ π} }}}}\left( {\sum\limits_{i = 1}^N {\frac{{M{\sigma _i}}}{{R_{1i}^2R_{2i}^2}}} } \right). $ | (3) |
式中:Pt为发射功率;Gt为发射天线功率增益;Gr为接收天线功率增益;λ为辐射源信号波长;N为地物分布的距离段数;M为每个距离段里面地物数量。
数字电视信号的波长较短,波长为0.6 m时,对一个几何尺寸为6×9=54 m2的地物(如建筑),若其前向散射系数为0.1,其RCS即可约为10 000 m2。假定参考天线的方位波束宽度为40°,对这样RCS的地物,在200 m距离范围内有10个,在500 m距离范围内有60个,在1 000 m距离范围内有120个,多径杂波功率与直达波功率相比即可达到-3 dB。当参考天线俯仰向波束也较宽时,可同时接收高度较高地物产生的多径杂波,进一步考虑到参考天线副瓣的影响,多径杂波与直达波功率相当是可能的。
以上采用全向散射模型分析了多径杂波的影响,当接收站附近地物导致反射多径直达波进入参考天线时,即使地物很少其强度也可能较大。
显然,多径直达波主要来自于近距离地物。接收站周围地形越开阔、直达波方向地物越少,参考天线的高度越高,波束越窄,副瓣越低,多径直达波的影响越小。为减少多径直达波的干扰,接收站的布设应避开城区并选择周围近距离没有高大建筑的区域。
1.2 多径杂波影响分析记直达波信号为s(n),多径杂波为s(n)延迟j个单元结果,αj为杂波强度系数,gx(n)、gy(n)分别为参考天线和主天线的噪声, n0为目标所在单元。于是参考天线信号为
| $ x\left( n \right) = s\left( n \right) + \sum\limits_j {{\alpha _j}} \cdot s\left( {n - j} \right) + {g_x}\left( n \right), $ | (4) |
假设主天线无杂波干扰,记为
| $ y\left( n \right) = s\left( {n - {n_0}} \right) + {g_y}\left( n \right), $ | (5) |
作主天线和参考天线的互相关
| $ {R_{yx}}\left( n \right) = y\left( n \right) * {x^ * }\left( { - n} \right) = {{R'}_{yx}}\left( n \right) + {R_{yp}}\left( n \right), $ | (6) |
| $ \begin{array}{l} {{R'}_{yx}} = \left[ {s\left( {n - {n_0}} \right) + {g_y}\left( n \right)} \right] * \left[ {s\left( { - n} \right) + } \right.\\ \;\;\;\;\;\;\;\;{\left. {{g_x}\left( { - n} \right)} \right)^ * }, \end{array} $ | (7) |
| $ \begin{array}{l} {R_{yp}}\left( n \right) = \left[ {s\left( {n - {n_0}} \right) + {g_y}\left( n \right)} \right] * \left( {\sum\limits_j {{\alpha _j}} \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;{\left. {s\left( { - n - j} \right)} \right)^ * } = s\left( {n - {n_0}} \right) * \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left( {\sum\limits_j {{\alpha _j} \cdot s\left( { - n - j} \right)} } \right)^ * } + {g_y}\left( n \right) * \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left( {\sum\limits_j {{\alpha _j} \cdot s\left( { - n - j} \right)} } \right)^ * }. \end{array} $ | (8) |
式中:R′yx为参考信号中无多径杂波影响时主天线信号和参考信号互相关结果;Ryp(n)为y(n)和参考信号中多径杂波部分互相关结果,即因多径杂波存在,产生的额外影响。
分析Ryp(n)共由两部分组成:
第一项为目标回波与多径杂波的互相关,将在n0-j位置引起虚警,虚警数目及强度取决于参考信号中多径杂波分布,多径杂波越强,虚警幅度越大;多径杂波越多,虚警越多。在互相关检测图中呈现出“目标分裂”、增加虚警现象。该现象不仅存在于运动目标检测,对静止杂波也有影响。
第二项为主天线噪声同多径杂波的互相关,将造成相关检测时噪声基底抬升,引起信噪比下降。
另外,主天线信号存在较强杂波时,在杂波位置附近也会产生虚警。通常主天线信号杂波抑制采用主参杂波对消方法,若参考信号含有多径杂波,会影响主天线杂波对消性能。
参考信号中多径杂波的存在,不仅会降低直达波的对消效果,产生虚假目标增加虚警概率,而且会和目标回波信号产生去相关失配损失。当多径杂波和直达波的功率相当时,参考信号和目标回波信号去相关失配损失约为2~3 dB,对系统的探测性能影响很大,必须对其进行提纯处理。参考通道中的多径杂波主要分布在近距离,数字电视信号带宽较大,相关处理后,对不同距离单元的多径杂波区分能力强,据该性质在时域滤波实现多径杂波抑制。
2 多径杂波抑制算法与原理 2.1 IIR滤波参考信号模型由式(4)给出,作z变换得
| $ \begin{array}{*{20}{c}} {X\left( z \right) = S\left( z \right)\left( {1 + \sum\limits_j {{\alpha _j} \cdot {z^{ - j}}} } \right) + {G_x}\left( z \right)}\\ { \Leftrightarrow S\left( z \right) = \frac{1}{{1 + \sum\limits_j {{\alpha _j} \cdot {z^{ - j}}} }}\left[ {X\left( z \right) - {G_x}\left( z \right)} \right]}\\ { \Leftrightarrow \frac{1}{{1 + \sum\limits_j {{\alpha _j} \cdot {z^{ - j}}} }}X\left( z \right) = S\left( z \right) + }\\ {\frac{1}{{1 + \sum\limits_j {{\alpha _j} \cdot {z^{ - j}}} }}{G_x}\left( z \right).} \end{array} $ | (9) |
理论上,将参考信号通过一个理想IIR滤波器可以得到较纯净直达波,其中IIR滤波器参数取决于多径分布。实际工作中IIR参数估计困难并且信道多变,以及IIR很难保证系统稳定性,采用自适应的FIR滤波器做提纯滤波。
2.2 k-前向预测考虑采用自适应滤波方法,自参照的进行杂波对消。输入为u(n),参照为d(n),滤波器权值为w,输出y(n)=wHu(n)。为分析简便,忽略噪声影响,参考信号表示为
| $ x\left( n \right) = s\left( n \right) + \sum\limits_j {{\alpha _j} \cdot s\left( {n - j} \right)} . $ | (10) |
记x(n)=[x(n), x(n-1), …, x(n-M+1)]T,M为滤波器长度。滤波器输入u(n)=x(n-k),训练参照
上述问题为维纳滤波问题,其最优解
| $ {\mathit{\boldsymbol{w}}_0} = {\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{p}}, $ | (11) |
其中
| $ \mathit{\boldsymbol{R}} = E\left[ {\mathit{\boldsymbol{u}}\left( n \right){\mathit{\boldsymbol{u}}^{\rm{H}}}\left( n \right)} \right],\mathit{\boldsymbol{p}} = E\left[ {\mathit{\boldsymbol{u}}\left( n \right){d^ * }\left( n \right)} \right] $ |
实际中考虑到训练成本以及信道多变的情况,d(n)无法实时获取,从而无法得到p。通常希望此滤波过程是自参照的,下面推导一定条件下可用p′=E[u(n)x*(n)]近似。
| $ \begin{array}{*{20}{c}} {E\left[ {\mathit{\boldsymbol{u}}\left( n \right){x^ * }\left( n \right)} \right] = E\left[ {\mathit{\boldsymbol{x}}\left( {n - i} \right){s^ * }\left( n \right)} \right] + }\\ {E\left[ {\mathit{\boldsymbol{x}}\left( {n - i} \right){{\left( {\sum\limits_j {{\alpha _j}s\left( {n - j} \right)} } \right)}^ * }} \right] = \mathit{\boldsymbol{\varepsilon }} + \mathit{\boldsymbol{p}},} \end{array} $ | (12) |
式(12)第一项ε为近似误差。
| $ \begin{array}{*{20}{c}} {\varepsilon \left( i \right) = E\left[ {x\left( {n - k - i} \right){s^ * }\left( n \right)} \right] = }\\ {E\left[ {\left( {s\left( {n - k - i} \right) + \sum\limits_j {{\alpha _j}s\left( {n - k - i - j} \right)} } \right){s^ * }\left( n \right)} \right] = }\\ {{r^ * }\left( {k + i} \right) + \sum\limits_j {{\alpha _j}{r^ * }\left( {k + i + j} \right)} .} \end{array} $ | (13) |
记r(i)为纯净直达波信号s(n)自相关函数在i处取值,则有
| $ \begin{array}{*{20}{c}} {p\left( i \right) = E\left[ {x\left( {n - k - i} \right){{\left( {\sum\limits_j {{\alpha _j}s\left( {n - j} \right)} } \right)}^ * }} \right]}\\ { = E\left[ {\left( {s\left( {n - k - i} \right) + \sum\limits_j {{\alpha _j}s\left( {n - k - i - j} \right)} } \right)} \right.}\\ {\left. {{{\left( {\sum\limits_m {{\alpha _m}s\left( {n - m} \right)} } \right)}^ * }} \right] = \sum\limits_m {{\alpha _m}{r^ * }\left( {k + i - m} \right)} + }\\ {\sum\limits_j {\sum\limits_m {{\alpha _j}{\alpha _m}{r^ * }\left( {k + i + j - m} \right)} } .} \end{array} $ | (14) |
若∀i∈[0, M-1], ε(i)→0,则p′→p。显然,若k较小,ε(0)=r*(k)落入直达波信号自相关主瓣,误差较大;同时k取值不宜太大,否则近处杂波将不会对消掉。通过观察参考信号自相关函数来选取k值,避开直达波自相关函数主瓣,可以得到良好的近似效果。特别的,当取k=1,则为常规的前向预测算法[8]。
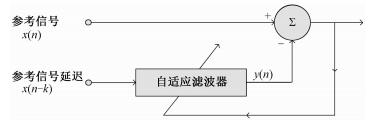
滤波器权值的求解可以通过最速下降、LMS、NLMS等方法,这里采用LMS自适应滤波,具有结构简单,运算量小的优势,算法结构如图 1所示。
|
Download:
|
| 图 1 k-前向预测算法结构图 Fig. 1 Schematic of k-forward prediction algorithm | |
外辐射源雷达采用数字电视信号时,具有带宽大、距离分辨率高的特性,其自相关函数通常主瓣较窄,副瓣较低。数字电视信号带宽约8 M,双基距离分辨率约为30 m,其纯净直达波的自相关函数可近似为主瓣稍宽的冲激函数。多径影响主要在近距离地物,实际系统工作中,可以通过选择工作场地,保证200 m以内无地物;假定多径杂波主要分布在近距离,双基距离3 km以内,一般取3≤k≤10,M≥128可满足实际需求。
3 算法性能评价原则通过第1节分析,参考信号中由于多径杂波的存在,会导致诸多问题,参考信号中多径杂波抑性能评价主要包括以下几个方面:
1) 参考信号自相关函数锐化;
2) 改善目标峰值信噪比;
3) 减少虚警数量;
4) 主参天线信号互相关函数多径杂波所在距离单元位置峰值得到抑制,如负半轴峰值数量减少。
4 仿真分析用高斯白噪声数据做仿真,分别仿真少量强多径杂波和多个弱多径杂波两种条件下算法性能。做参考信号和主天线信号互相关,考察理想情况、多径抑制前、多径抑制后目标峰值信噪比PSNRideal、PSNRoriginal、PSNRk-LMS,依据第3节所提原则,评价该算法提纯性能。
4.1 两个强多径杂波条件下参考天线直达波信号信噪比10 dB,两个强多径杂波位于20、25点位置,杂噪比7 dB。
主天线仿真包含直达杂波(杂噪比-5 dB)、静目标1(信噪比-7 dB,位于71点位置),静目标2(信噪比-12 dB,位于191点位置)。信号长度为100 000点;滤波器选取LMS自适应滤波器,输入x(n-k),参照x(n),步长μ=10-4,长度M=128,据上述参数仿真如图 2所示。

|
Download:
|
| 图 2 参考信号存在两个强多径杂波的仿真 Fig. 2 Simulation of two strong multi-path clutter in the reference signal | |
图 2仿真表明,多径杂波将引起相关处理底噪抬升,导致峰值信噪比下降。当信噪比3 dB时,未提纯参考信号与主天线信号互相关,PSNR降低1.83 dB。
参考信号自相关函数主瓣较宽(约占10个单元,单侧为5个单元),多径抑制前参考信号和主天线信号互相关图中,在目标位置左侧有明显峰值,此时会产生虚警。采用LMS自适应滤波,分别做k=1,2,…,16的前向预测。
多径杂波所在距离单元处峰值有明显下降,说明多径杂波得到抑制;PSNR改善较小,是由于滤波输出y(n)中除参考信号中多径成份外,包含较多直达波成份,导致e(n)中直达波损失引起。
表 1给出当前仿真条件下,应用该算法提纯后,零距离点信噪比随k值变化情况。当k取8时多径杂波抑制效果最优,此时ε较小。图 2(b)、2(d)比较可知,该提纯算法对多径杂波抑制大于10 dB,降低了虚警;目标PSNR较杂波抑制前有1.36 dB提升(理论最优值1.83 dB),效果较为理想,提高了目标检测性能。
|
|
表 1 信噪比随k值变化 Table 1 Variation in SNR with k |
参考信号信杂比0 dB,信噪比10 dB,30个弱多径杂波随机分布于10~100点位置;主天线仿真同上。滤波器选取LMS自适应滤波器,输入x(n-k),参照x(n),步长μ=10-4,长度M=256,据上述参数仿真如图 3所示。
|
Download:
|
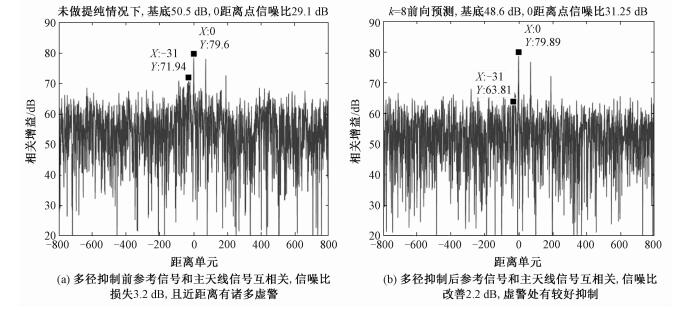
| 图 3 仿真多个多径时该算法多径杂波抑制效果 Fig. 3 Simulation of multiple multi-path clutter in the reference signal | |
图 3仿真结果表明,多个弱多径杂波存在于参考信号中,将引起近距离处产生诸多弱虚警。当直达波功率和多径杂波功率相当时,主参信号互相关处理结果的检测基底抬升约3.2 dB。本文算法可以有效抑制多径,多径杂波所在距离单元处因杂波与直达波匹配产生的峰值可以抑制到噪声水平,降低虚警;目标PSNR有2.2 dB改善。
4.3 信噪比、信杂比对算法影响因算法对噪声或有放大作用,即使抑制了多径杂波,但也可能会带来目标检测信噪比下降的情况。定义峰值信噪比改善比率为
| $ \rho = \frac{{{\rm{PSN}}{{\rm{R}}_{{\rm{LMS}}}}}}{{{\rm{PSN}}{{\rm{R}}_{{\rm{ideal}}}}}} \times 100\% . $ | (15) |
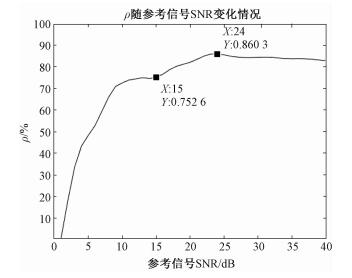
ρ越接近100%,峰值信噪比改善越接近理想情况,即直达波提纯效果越好。仿真参考天线信号信杂比1.2 dB,信噪比取0~40 dB,验证算法对峰值信噪比的改善能力如图 4所示。
|
Download:
|
| 图 4 ρ随参考信号中信噪比变化情况 Fig. 4 Variation in ρ with SNR in the reference signal | |
由图 4可知,该算法对于目标峰值信噪比改善能力受参考信号信噪比影响。当信噪比0 dB以下时,甚至会出现恶化,ρ < 0。随着参考信号信噪比升高,目标峰值信噪比改善情况趋于稳定。参考信号信噪比10 dB时,ρ>70%;信噪比30 dB时,ρ>80%。
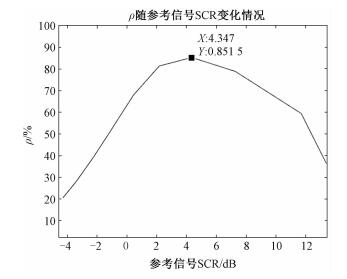
通常参考信号中信噪比10 dB的条件容易满足,此时该算法工作良好,在此条件下考察参考信号信杂比变化对目标峰值信噪比改善情况如图 5所示。
|
Download:
|
| 图 5 ρ随参考信号中信杂比变化情况 Fig. 5 Variation in ρ with SCR in the reference signal | |
由图 5可知,参考信号中信噪比为10 dB条件下,当信杂比较低时,本文算法对多径杂波抑制效果良好,有ρ>80%,且随信杂比增加,PSNR接近理想值;当信杂比较高时,该算法改善效果变得不显著。事实上,当信杂比较高时,杂波对于目标检测影响变得很小,直达波提纯工作不再是主要问题。
5 实际数据处理实际数据采样率Fs=10 MHz,取0.01 s数据,k=8,M=128,采用LMS算法提纯参考信号。做提纯前后参考信号自相关、参考信号和主天线信号互相关如下。
本文算法的k值选取与待处理信号的具体形式有关。如图 6(a)所示,该数字电视信号实际数据在保证了在300 m距离内地物较少,即1~10距离单元点内多径杂波较少,其自相关函数在近距离内较为锐利,但主瓣仍有约为5距离单元的宽度,这与信号具体形式以及采样率有密切关联,应用本文算法选取k值时要避开主瓣范围。自相关函数图中,在30距离点附近有明显峰值,这主要是由于多径杂波的影响。0.3~3 km距离范围内的多径杂波对目标检测影响较为显著,因此参考通道直达波提纯工作将主要在该距离范围内进行。
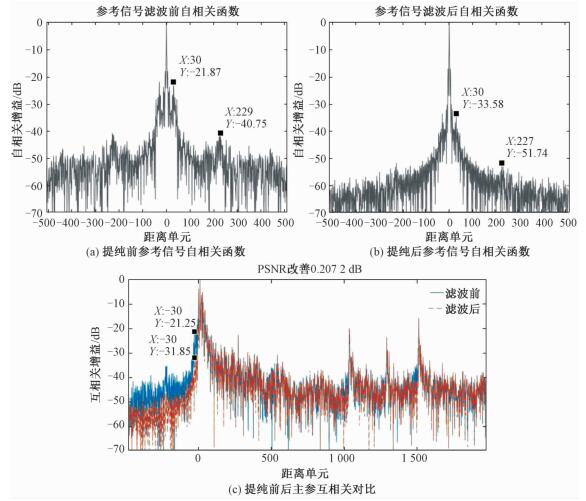
|
Download:
|
| 图 6 实际数据处理结果 Fig. 6 Real-life data processing results | |
通过多次预处理,选取合适的k值以及滤波器长度M,该算法可在实际数据中表现出良好性能。其中k值决定该算法的提纯性能,而M则决定滤波器抑制多径杂波的距离范围。
如图 6(b)所示,实际数据处理过程中,提纯后参考信号自相关函数整体变锐利,多径杂波所在距离单元峰值有明显下降,说明多径杂波得到抑制。
此外,图 6(c)中虚线标出互相关直达波左侧、静目标回波左侧的峰值均有衰减,降低了虚警,同样说明多径杂波得到抑制,其中-30点位置多径杂波抑制大于10 dB,零距离处峰值信噪比有0.21 dB改善。应用该算法,外辐射源雷达环境适用性提高,目标检测能力有所改善。
6 结束语本文介绍的参考信号提纯方法为自参照的基于LMS自适应滤波方法,适应于参考天线仅为单通道,或者参考天线为阵列天线做DBF之后的情况。依据数字电视信号自相关函数与冲激函数接近的特点,选取合适k值,实现在时域滤波对消参考信号中的多径成分。需要注意的是,本文对消采用的是LMS自适应滤波方法,对消效果对步长λ较为敏感。文中λ的选取为经验值,λ的取值特性有待做进一步的研究。
在少量强多径杂波以及大量弱多径杂波两种不同信道情况下,该算法都能良好工作,说明该算法具有良好的适用性。相对于先用训练序列对信道进行估测的方式,由于本文提出的算法为自参照的,可以应对信道不稳定的情形。当已知信道较为稳定的情况下,可以考虑在滤波器权系数收敛后,将实时滤波结构改为非实时滤波结构,从而降低运算量。
| [1] |
王峰, 魏爽, 蒋德富, 等. 基于稀疏超指数盲均衡的高频外辐射源雷达发射信号提取[J]. 电波科学学报, 2016, 31(4):818–823.
|
| [2] |
李纪传. 无源雷达杂波对消关键技术及目标检测方法研究[D]. 北京: 中国科学院文献情报中心, 2015.
|
| [3] |
Cardinali R, Colone F, Ferretti C, et al. Comparison of clutter and multipath cancellation techniques for passive radar[C]//Proc of the IEEE Radar Conference. Boston: IEEE. 2007: 17-20.
|
| [4] |
李纪传, 吕晓德, 向茂生, 等. 等效凹槽滤波器及其在无源相关定位雷达中的应用[J]. 雷达学报, 2014, 3(6):675–685.
|
| [5] |
吴海洲, 陶然, 单涛. 基于DTTB照射源的无源雷达直达波干扰抑制[J]. 电子与信息学报, 2009, 31(9):2033–2038.
|
| [6] |
万显荣, 岑博, 易建新, 等. 中国移动多媒体广播外辐射源雷达参考信号获取方法研究[J]. 电子与信息学报, 2012, 34(2):338–343.
|
| [7] |
杨建广, 吴道庆. 调频广播台直达波与地杂波强度分析[J]. 现代雷达, 2005, 27(12):33–36.
DOI:10.3969/j.issn.1004-7859.2005.12.009 |
| [8] |
赫金. 自适应滤波器原理[M]. 4版. 郑宝玉, 等, 译. 北京: 电子工业出版社, 2010.
|
 2018, Vol. 35
2018, Vol. 35 


