由于银河系的晕比盘有更长的动力学时标[1-2],它可以记录更多银河系形成和演化的历史,所以对银河系晕的研究一直是星系研究的重要课题。在标准冷暗物质宇宙模型中,银河系晕通过吸积作用形成。通过对晕星金属丰度的研究分析,可以给出银河系晕形成更加具体直接的限制。
SDSS[3]和2MASS[4]等大规模巡天项目的开展和运行给我们提供了大量关于恒星金属丰度和运动学的数据。十几年来对巡天数据的分析研究,我们对银河系晕的认识也有显著提高。
Carollo等[5-6]选择SDSS和SEGUE中太阳邻域(dhelio<4 kpc和7 kpc<R<10 kpc)的恒星作为样本星,通过对样本星金属丰度和运动学的研究,发现银河系的晕是由内晕和外晕两个相互重叠的成分组成的。An等[7]分析SDSS Stripe 82中5 kpc<dhelio<8 kpc恒星测光金属丰度分布,发现晕星的[Fe/H]的分布可以用双高斯模型描述。An等[8]用更加完备的Stripe 82的恒星样本对金属丰度分布进行再次研究,得到相同的结论。近年来越来越多的工作[9-11]支持银河系的双晕模型。
恒星的金属丰度分布对研究银河系的双晕性至关重要。光谱数据和测光数据都可以得到恒星的金属丰度,其中测光数据较光谱数据有更好的覆盖范围和观测深度,所以在研究银河系晕时测光金属丰度更具优势。Ivezć等[12]利用F/G型主序星通过多项式拟合得到测光金属丰度与色指数u-g,g-r之间的关系。Gu等[13]采用蒙特卡罗方法模拟恒星测光金属丰度分布。该方法在贫金属端比多项式拟合更有优势。
本文结合蒙特卡罗方法和SCUSS,SDSS测光数据对银河系晕的金属丰度分布进行研究。
1 SCUSS和SDSS简介斯隆数字化巡天(SDSS)是由美国国家费米实验室等8个研究机构共同实施的多波段测光与光谱巡天项目。该项目利用美国墨西哥州的阿帕奇天文台的一架2.5 m口径广角光学望远镜[14]。至今,测光巡天已经覆盖超过1/3的天区。测光巡天共有u,g,r,i和z这5个波段,有效波长分别为355.1,468.6,616.5,748.1和893.1 nm。5个波段的极限星等分别是22.0,22.2,22.2,21.3和20.5 mag。
南银冠u波段巡天(SCUSS)是由中国科学院国家天文台和美国亚利桑那大学共同实施的国际合作项目。该项目利用口径为2.3 m的博克望远镜(Bok telescope)在u波段(355 nm)对南银冠进行测光巡天观测。同时该项目将为LAMOST(large sky area multi-object fiber spectroscopic telescope)巡天项目提供输入星表。最终该巡天覆盖近5 000 deg2的南银冠天区。u波段的极限星等大约是23.5 mag[15],比SDSS的u波段极限星等深1.5 mag。
2 测光金属丰度定标本节介绍基于蒙特卡罗模拟对恒星测光金属丰度定标的方法。将SDSS网站(http://www.sdss3.org/)中sppParams星表与SCUSS测光数据通过ID匹配得到样本,该样本有表面重力、金属丰度、有效温度等光谱信息和SDSS和SCUSS的测光信息。为选择定标样本,采用与文献[12]类似的筛选标准:
1) r波段消光小于0.3;
2) log(g)>3;
3) 14<g<19.5和U<22.5;
4) 0.1<g-r<0.7和-0.2<0.35(g-r)-(r-i)<0.1;
5) 0.6<U-g<2和-0.25<(g-r)-0.5(U-g)<0.05;
其中各波段测光都已经过消光改正,自此之后U表示SCUSS的u波段测光。此外,利用Jurić等[16]提到的主序星条件,最终得到42 767个定标样本。
采用与文献[13]类似的方法将色指数平均分开并按下面公式赋予index值,其中int表示取整。index=12×int((U-g-0.6)/0.05)+int((g-r-0.1)/0.05)同时也将[Fe/H]从-3.5到0.5按0.05 dex均分,得到维度为336×80的“种子”数组。
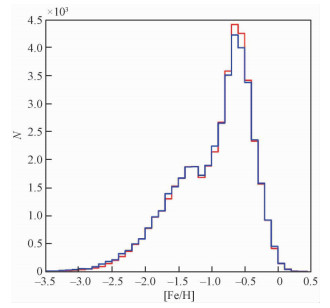
根据恒星的色指数U-g,g-r和得到的“种子”数组,可以利用蒙特卡罗模拟产生随机数的方法产生恒星测光技术丰度的分布。如图 1所示,由蒙特卡罗模拟的定标样本的测光金属丰度分布(蓝色柱状图)和光谱(红色柱状图)给出的金属丰度分布十分相似。
|
Download:
|
| 图 1 测光金属丰度分布(蓝色柱状图)与光谱金属丰度(红色柱状图)分布的对比 Fig. 1 Comparison between the metallicity distributions based on photometry (solidhistogram) and based on spectra (dashed histogram) | |
在本文中选择F/G型主序拐点星作为示踪星,具体选择过程如下。同样利用Jurić等[16]提到的主序星条件。避免CCD饱和和低信噪比,限制14.5<r<21.5,去除(r-i)>1.8的样本使得测光视差公式更加可靠。为了运用蒙特卡罗方法,还采用定标样本筛选条件的4)、5)。还限制0.2<g-r<0.4,15<g<21,U<22完成星等及色指数选择。
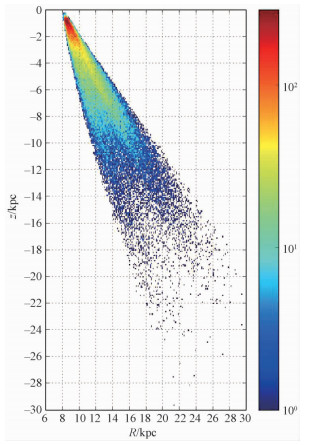
银河系晕中除场星之外还有星流、星云之类的子结构。Gu等[17]提到子结构在20.5<g<21星等区间内可以较为清楚地分辨出来。如图 2所示,选择20.5<g<21的子样本并画出样本在银经银维平面的数密度分布。图中虚线围成的两个区域分别是人马座星流(Sagittarius stream)和武仙座-天鹰座星云(Hercules-Aquila cloud),而实线围成的区域则是最终样本所在的位置,这样就减少子结构对测光金属丰度分布的影响。综合以上所有选择条件最终得到78 092个样本。图 3显示的是样本在以银心为原点的柱坐标RZ平面中的数密度分布,其中太阳的坐标是(R, Z, φ)=(8.0 kpc, 0, 0)。

|
Download:
|
| 图中实线为样本所在区域。 图 2 主序星(20.5<g<21)在lb平面内的分布 Fig. 2 Space distribution of main-sequence stars with 20.5 < g < 21 | |
|
Download:
|
| 图 3 样本星在RZ平面内的分布 Fig. 3 Distribution of sample stars in RZ | |
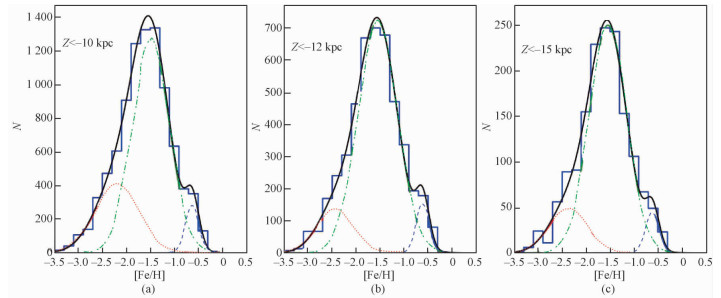
运用蒙特卡罗方法可以得到样本的测光金属丰度分布。选择远离盘的样本研究金属丰度分布与柱坐标中Z的关系,样本分别满足Z<-10 kpc,Z<-12 kpc和Z<-15 kpc。假设单一星族的金属丰度分布可以用高斯函数描述,那么对于晕星的金属丰度分布则可以用混合高斯模型描述。图 4展示最终结果,具体细节如下。
|
Download:
|
| 虚线、点线和点划线3条曲线代表高斯函数,3个高斯函数之和为黑色曲线 图 4 不同Z区间的测光金属丰度分布 Fig. 4 Photometric metallicity distributions in different Z-intervals | |
图 4中柱状图为测光金属丰度分布,虚线、点线和点划线3条曲线代表高斯函数。图 4(a)显示Z<-10 kpc子样本,点划线的峰值位于[Fe/H]=-1.49,弥散为σ[Fe/H]=0.39,所占权重为68%;点线的峰值位于[Fe/H]=-2.19,弥散为σ[Fe/H]=0.46,所占权重为26%;虚线的峰值位于[Fe/H]=-0.62,弥散为σ[Fe/H]=0.14,所占权重为6%。图 4(b)显示Z<-12 kpc子样本,点划线的峰值位于[Fe/H]=-1.55,弥散为σ[Fe/H]=0.41,所占权重为80%;点线的峰值位于[Fe/H]=-2.43,弥散为σ[Fe/H]=0.38,所占权重为14%;虚线的峰值位于[Fe/H]=-0.61,弥散为σ[Fe/H]=0.14,所占权重为6%。图 4(c)显示Z<-15 kpc子样本,点划线的峰值位于[Fe/H]=-1.54,弥散为σ[Fe/H]=0.39,所占权重为79%;点线的峰值位于[Fe/H]=-2.37,弥散为σ[Fe/H]=0.40,所占权重为16%;虚线的峰值位于[Fe/H]=-0.61,弥散为σ[Fe/H]=0.14,所占权重为5%。表 1是以上结论的总结。
|
|
表 1 高斯模型拟合参数 Table 1 Parameters of Gaussian model fitness |
An等[7-8]基于SDSS的Stripe82恒星的测光金属丰度分布并用双高斯模型拟合,其峰值位于[Fe/H]≈-1.40和≈-1.90。对比本文结果,可以认为两个贫金属成分是内外晕的贡献。现有测光金属丰度分布中存在一个-1.0<[Fe/H]<-0.3富金属成分。Gu等[17]提到人马座星流的测光金属丰度大致从[Fe/H]≈-1.0到[Fe/H]≈-0.5分布。基于Stripe82星表中的RR变星, Watkins等[18]指出武仙座-天鹰座星云有更贫的金属丰度。所以富金属成分可能是人马座星流对样本污染导致的。
4 总结本文中,基于SCUSS和SDSS光谱和测光数据,筛选出42 767个定标样本,经处理得到反映金属丰度和色指数相关性的“种子”数组。限制色指数和视星等以得到F/G型主序星,为减少子结构对结果的影响,限制银经银纬范围,最终得到78 092个样本。选择位于不同的Z范围的样本,研究银河系晕的测光金属丰度分布与Z的关系。得到金属丰度分布都可以用三峰高斯模型拟合且模型的峰值位于[Fe/H]~-0.60,-1.55和-2.20。经过对比分析,发现两个贫金属峰是内外晕的贡献,而较富成分则对应晕中子结构的影响。该结果在金属丰度分布方面为证明银河系的双晕性提供了补充证据。
| [1] |
Johnston K V, Hernquist L, Bolte M. Fossil signatures of ancient accretion events in the halo[J]. ApJ, 1996, 465:278–287.
DOI:10.1086/177418 |
| [2] |
Mayer L, Quinn T, Governato F, et al. Tidal debris of dwarf spheroidals as a probe of structure formation models[J]. MNRAS, 2002, 336(1):119–130.
DOI:10.1046/j.1365-8711.2002.05721.x |
| [3] |
Yanny B, Newberg H J, Johnson J A, et al. Tracing Sagittarius structure with SDSS and SEGUE imaging and spectroscopy[J]. ApJ, 2009, 700(2):1282–1298.
DOI:10.1088/0004-637X/700/2/1282 |
| [4] |
Majewski S R, Skrutskie M F, Weinberg M D, et al. A two micron all sky survey view of the Sagittarius Dwarf galaxy. Ⅰ. Morphology of the Sagittarius core and tidal arms[J]. ApJ, 2003, 599(2):1082–1115.
DOI:10.1086/apj.2003.599.issue-2 |
| [5] |
Carollo D, Beers T C, Lee Y S, et al. Two stellar components in the halo of the Milky Way[J]. Nature, 2007, 450(7172):1020–1025.
DOI:10.1038/nature06460 |
| [6] |
Carollo D, Beers T C, Chiba M, et al. Structure and kinematics of the stellar halos and thick disks of the Milky Way based on calibration stars from sloan digital sky survey DR7[J]. ApJ, 2010, 712(1):692–727.
DOI:10.1088/0004-637X/712/1/692 |
| [7] |
An D, Beers T C, Johnson J A, et al. The stellar metallicity distribution function of the Galactic halo from SDSS photometry[J]. ApJ, 2013, 763(1):65–87.
DOI:10.1088/0004-637X/763/1/65 |
| [8] |
An D, Beers T C, Santucci R M, et al. The fractions of inner-and outer-halo stars in the local volume[J]. ApJL, 2015, 813(2):L28–L33.
DOI:10.1088/2041-8205/813/2/L28 |
| [9] |
Chen Y Q, Zhao G, Carrell K, et al. Red giant stars from sloan digital sky survey. I. The general field[J]. ApJ, 2014, 795(1):52–64.
DOI:10.1088/0004-637X/795/1/52 |
| [10] |
Das P, Binney J. Characterizing stellar halo populations-I. An extended distribution function for halo K giants[J]. MNRAS, 2016, 460(2):1725–1738.
DOI:10.1093/mnras/stw744 |
| [11] |
Helmi A, Veljanoski J, Breddels M A, et al. A box full of chocolates:the rich structure of the nearby stellar halo revealed by Gaia and RAVE[J]. A & A, 2017, 598:A58–A75.
|
| [12] |
Ivezić Ž, Sesar B, Jurić M, et al. The Milky Way tomography with SDSS Ⅱ stellar metallicity[J]. ApJ, 2008, 684(1):287–325.
DOI:10.1086/529168 |
| [13] |
Gu J Y, Du C H, Jing Y J, et al. A Monte-Carlo method for estimating stellar photometric metallicity distributions[J]. ApJ, 2016, 826(1):36–41.
DOI:10.3847/0004-637X/826/1/36 |
| [14] |
Gunn J E, Siegmund W A, Mannery E J, et al. The 2.5 m telescope of the sloan digital sky survey[J]. AJ, 2006, 131(4):2332–2359.
DOI:10.1086/500975 |
| [15] |
Jia Y P, Du C H, Wu Z Y, et al. Estimation of absolute magnitude-dependent Galactic model parameters in intermediate latitude with SDSS and SCUSS[J]. MNRAS, 2014, 441(1):503–512.
DOI:10.1093/mnras/stu469 |
| [16] |
Jurić M, Ivezić Ž, Brooks A, et al. The Milky Way tomography with SDSS. Ⅰ. Stellar number density distribution[J]. ApJ, 2008, 673(2):864–914.
DOI:10.1086/523310 |
| [17] |
Gu J Y, Du C H, Jia Y P, et al. Photometric metallicity calibration with SDSS and SCUSS and its application to distant stars in the south Galactic cap[J]. MNRAS, 2015, 452(3):3092–3099.
DOI:10.1093/mnras/stv1529 |
| [18] |
Watkins L L, Evans N W, Belokurov V, et al. Substructure revealed by RRLyraes in SDSS Stripe 82[J]. MNRAS, 2009, 398(4):1757–1770.
DOI:10.1111/mnr.2009.398.issue-4 |
 2018, Vol. 35
2018, Vol. 35 


