时间相关的Hartree-Fock(TDHF)理论最早由狄拉克于1930年提出[1],它是基于自洽平均场近似的微观量子多体理论, 该理论成功地用于研究熔合反应[2-4]、深度非弹散射[5-8]、巨共振[9-10]、准裂变[11]等多种核物理现象。
近年来,张量力效应成为原子核物理领域的一个热门研究课题。张量力效应在原子核结构性质的描述方面起着非常重要的作用[12],从平均场理论相关研究可以知道,张量力对自旋-轨道劈裂[13-15]以及丰中子核中可能出现的新幻数[16]有很大的影响,Otsuka等[17-19]发现在奇异核壳层演化过程中,张量力能够很好地解释核子单粒子能级的演化。
上面这些都是有关张量力在原子核结构与性质方面的研究,很少有研究涉及到张量力对重离子碰撞的影响,大多数理论模型在重离子碰撞中都忽略张量力的贡献。Stevenson等[20]对张量力在16O+16O反应的研究中,发现张量力对熔合阈值和Skyrme能量密度泛函中各项能量贡献的影响是不可忽略的。Dai等[21]研究张量力对16O+16O体系能量耗散和熔合截面的影响,发现能量耗散的大小依赖于Skyrme参数的选择;另外还发现未包含张量力的SLy5参数计算的16O+16O熔合截面比实验值大将近25%,而包含张量力的T11参数计算得到的16O+16O熔合截面与实验值符合得很好。
但是张量力在其他反应体系中的动力学效应还不是很清楚,本文采用包含有完整张量力项的Skyrme有效作用,和THFD理论研究16O+40Ca体系中张量力对库仑位垒、高能熔合阈值以及Skyrme能量密度泛函中各项能量贡献的影响。
1 理论方法Hartree-Fock理论是一种平均场近似理论,在平均场近似下,剩余相互作用被略去,每一个粒子在平均场中做独立运动。Hartree-Fock方程可以通过变分法得到
| $ \mathit{\hat{h}}{{\mathit{\psi }}_{\mathit{\lambda }}}\text{=}{{\epsilon }_{\mathit{\lambda }}}{{\mathit{\psi }}_{\mathit{\lambda }}}\text{, } $ | (1) |
式中:ψλ是单粒子态ϵλ的能量;
| $ \mathit{S}\text{=}\int_{{{\mathit{t}}_{1}}}^{{{\mathit{t}}_{\text{2}}}}{\text{d}\mathit{t}}\langle \mathit{\psi }\text{(}\mathit{\boldsymbol{r}}\text{, }\mathit{t}\text{) } | \mathit{H}\text{-i}\hbar {{\partial }_{\mathit{t}}} | \mathit{\psi }\text{(}\mathit{\boldsymbol{r}}\text{, }\mathit{t}\text{)}\rangle \text{, } $ | (2) |
式中:H为多体哈密顿量算符;ψ(r, t)为多体波函数,在平均场近似下,可以表达为单粒子波函数φλ(r, t)的Slater行列式。通过对作用量S求变分δS/δψ*=0,可以得到TDHF方程
| $ \text{i}\hbar {{\partial }_{\mathit{t}}}{{\phi }_{\mathit{\lambda }}}\text{=}\hbar {{\phi }_{\mathit{\lambda }}}\text{, }\mathit{\lambda }\text{=1, }\cdots \text{, }\mathit{N}\text{.} $ | (3) |
目前大多数Hartree-Fock和TDHF计算,采用Skyrme有效相互作用[22],Skyrme相互作用最早是由Skyrme于20世纪50年代提出[22-25],之后Skyrme给出含参数的Skyrme有效作用势,现在的Skyrme有效作用势已经有几十套常用的参数,例如SkM*[26], SLy4d[27], SLy5[28], SLy5t[28]和TIJ[29]等。完整的Skyrme相互作用势为
| $ \begin{align} &\ \ \ \ {{\mathit{\boldsymbol{\upsilon }} }_{\mathit{SK}}}\left( {{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{, }{{\mathit{\boldsymbol{r}}}_{\text{2}}} \right)\text{=}{{\mathit{t}}_{\text{0}}}\left( \text{1+}{{\mathit{x}}_{\text{0}}}{{{\mathit{\hat{P}}}}_{\mathit{\sigma }}} \right)\mathit{\delta }\left( {{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}} \right)\text{+} \\ &\frac{\text{1}}{2}{{\mathit{t}}_{\text{1}}}\text{(1+}{{\mathit{x}}_{\text{1}}}{{{\mathit{\hat{P}}}}_{\mathit{\sigma }}}\text{) } [ {{{\mathit{\boldsymbol{{k}'}}}}^{\text{2}}}\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)}\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)}{{\mathit{k}}^{\text{2}}} ] \text{ +} \\ &\ \ \ \ \ \ \ \ \ \ \ {{\mathit{t}}_{\text{2}}}\text{(1+}{{\mathit{x}}_{\text{2}}}{{{\mathit{\hat{P}}}}_{\mathit{\sigma }}}\text{)}\mathit{\boldsymbol{{k}'}}\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)}\mathit{\boldsymbol{k}}\text{+} \\ &\ \ \ \ \frac{\text{1}}{\text{6}}{{\mathit{t}}_{\text{3}}}\text{(1+}{{\mathit{x}}_{\text{3}}}{{{\mathit{\hat{P}}}}_{\mathit{\sigma }}}\text{)}{{\mathit{\rho }}^{\mathit{\alpha }}}\left( \frac{{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{+}{{\mathit{\boldsymbol{r}}}_{\text{2}}}}{\text{2}} \right)\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)+} \\ &\ \ \ \ \ \ \ \ \ \ \text{i}{{\mathit{W}}_{\text{0}}}\text{(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{1}}}\text{+}{{\mathit{\boldsymbol{ \sigma }} }_{\text{2}}}\text{) } \cdot \mathit{\boldsymbol{{k}'}} \times \mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)}\mathit{\boldsymbol{k}}\text{+} \\ &\ \ \ \frac{{{\mathit{t}}_{\text{e}}}}{2} \{ [ \text{ 3(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{1}}} \cdot \mathit{\boldsymbol{{k}'}}\text{)(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{2}}} \cdot \mathit{\boldsymbol{{k}'}}\text{)-(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{1}}} \cdot {{\mathit{\boldsymbol{ \sigma }} }_{\text{2}}}\text{)}{{{\mathit{\boldsymbol{{k}'}}}}^{\text{2}}} ] \\ &\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)+}\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{) } [ \text{ 3(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{1}}} \cdot \mathit{\boldsymbol{k}}\text{)(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{2}}} \cdot \mathit{\boldsymbol{k}}\text{)-} \\ &\ \ \ \ \ \ \text{(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{1}}} \cdot {{\mathit{\boldsymbol{ \sigma }} }_{\text{2}}}\text{)}{{\mathit{\boldsymbol{k}}}^{\text{2}}} ] \} \text{ +}{{\mathit{t}}_{\text{o}}} [ \text{ 3(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{1}}} \cdot \mathit{\boldsymbol{{k}'}}\text{)}\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)} \\ &\ \ \ \ \ \ \ \ \ \text{(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{2}}} \cdot \mathit{\boldsymbol{k}}\text{)-(}{{\mathit{\boldsymbol{ \sigma }} }_{\text{1}}} \cdot {{\mathit{\boldsymbol{ \sigma }} }_{\text{2}}}\text{)}\mathit{\boldsymbol{{k}'}}\mathit{\delta }\text{(}{{\mathit{\boldsymbol{r}}}_{\text{1}}}\text{-}{{\mathit{\boldsymbol{r}}}_{\text{2}}}\text{)}\mathit{\boldsymbol{k}} ] \\ \end{align} $ | (4) |
式中:ti, xj(i,j=0, 1, 2, 3), to, te和W0是Skyrme力的系数,其中k和k′定义为
| $ \mathit{\boldsymbol{k}}\text{=-}\frac{\text{(}{{\nabla }_{\text{1}}}\text{-}{{\nabla }_{\text{2}}}\text{)}}{\text{2}\mathit{i}}\text{, } ~ \mathit{\boldsymbol{{k}'}}\text{=}\frac{\text{(}{{\nabla }_{\text{1}}}\text{-}{{\nabla }_{\text{2}}}\text{)}}{\text{2}\mathit{i}}\text{.} $ |
对应的Skyrme能量密度泛函为
| $ \begin{align} &\ \ \ \ \ \mathit{E}\text{=}\int{{{\text{d}}^{\text{3}}}}\mathit{\boldsymbol{r}}\mathit{H}\text{(}\mathit{\rho }\text{, }\mathit{\tau }\text{, }\mathit{\boldsymbol{j}}\text{, }\mathit{\boldsymbol{s}}\text{, }\mathit{\boldsymbol{T}}\text{, }\mathit{\boldsymbol{J}}\text{, }\mathit{\boldsymbol{F}}\text{;}\mathit{\boldsymbol{r}}\text{)=} \\ &\int{{{\text{d}}^{\text{3}}}}\mathit{\boldsymbol{r}}\sum\limits_{\mathit{t}\text{=0, 1}}{ \{ }\mathit{A}_{\mathit{t}}^{\mathit{\rho }} [ {{\mathit{\rho }}_{\text{0}}} ] \mathit{\rho }_{\mathit{t}}^{2}\text{+}\mathit{A}_{\mathit{t}}^{\Delta \mathit{\rho }}{{\mathit{\rho }}_{\mathit{t}}} \Delta {{\mathit{\rho }}_{\mathit{t}}}\text{+}\mathit{A}_{\mathit{t}}^{\mathit{\tau }}{{\mathit{\rho }}_{\mathit{t}}}{{\mathit{\tau }}_{\mathit{t}}}\text{+} \\ &\ \ \ \ \mathit{A}_{\mathit{t}}^{\Delta \mathit{s}}{{\mathit{\boldsymbol{s}}}_{\mathit{t}}} \cdot \Delta \mathit{\boldsymbol{s}}\text{+}\mathit{A}_{\mathit{t}}^{\text{T}}{{\mathit{\boldsymbol{s}}}_{\mathit{t}}} \cdot {{\mathit{\boldsymbol{T}}}_{\mathit{t}}}\text{+}\mathit{A}_{\mathit{t}}^{\nabla \mathit{J}}{{\mathit{\rho }}_{\mathit{t}}}\nabla \cdot {{\mathit{\boldsymbol{J}}}_{\mathit{t}}}\text{+} \\ &\ \ \ \ \ \mathit{A}_{\mathit{t}}^{\mathit{s}} [ {{\mathit{\rho }}_{\text{0}}} ] \mathit{\boldsymbol{s}}_{\mathit{t}}^{2}\text{-}\mathit{A}_{\mathit{t}}^{\mathit{\tau }}\mathit{\boldsymbol{j}}_{\mathit{t}}^{2}\text{-}\mathit{A}_{\mathit{t}}^{\text{T}}\sum\limits_{\mathit{\mu }\text{, }\mathit{\upsilon }\text{=}\mathit{x}}^{\mathit{z}}{{{\mathit{J}}_{\mathit{t}\text{, }\mathit{\mu \upsilon } ~ }}{{\mathit{J}}_{\mathit{t}\text{, }\mathit{\mu \upsilon } ~ }}}\text{+} \\ &\mathit{A}_{\mathit{t}}^{\nabla \mathit{J}}{{\mathit{\boldsymbol{s}}}_{\mathit{t}}} \cdot \nabla \times {{\mathit{\boldsymbol{j}}}_{\mathit{t}}}\text{-}\mathit{B}_{\mathit{t}}^{\text{T}}\sum\limits_{\mathit{\mu }\text{, }\mathit{\upsilon }\text{=}\mathit{x}}^{\mathit{z}}{{{\mathit{J}}_{\mathit{t}\text{, }\mathit{\mu \upsilon } ~ }}{{\mathit{J}}_{\mathit{t}\text{, }\mathit{u\upsilon } ~ }}}\text{+}\mathit{B}_{\mathit{t}}^{\text{F}}{{\mathit{\boldsymbol{s}}}_{\mathit{t}}} \cdot {{\mathit{\boldsymbol{T}}}_{\mathit{t}}}\text{-} \\ &\ \ \ \ \ \frac{\text{1}}{2}\mathit{B}_{\mathit{t}}^{\text{F}}\sum\limits_{\mathit{\mu }\text{, }\mathit{\upsilon }\text{=}\mathit{x}}^{\mathit{z}}{{{\mathit{J}}_{\mathit{t}\text{, }\mathit{\mu \upsilon } ~ }}{{\mathit{J}}_{\mathit{t}\text{, }\mathit{\upsilon \mu } ~ }}}\text{-}\frac{1}{2}\mathit{B}_{\mathit{t}}^{\text{F}}{{\text{(}\sum\limits_{\mathit{\mu }\text{=}\mathit{x}}^{\mathit{z}}{{{\mathit{J}}_{\mathit{t}\text{, }\mathit{\mu \mu } ~ }}}\text{)}}^{\text{2}}}\text{+} \\ &\ \ \mathit{B}_{\mathit{t}}^{\text{F}}{{\mathit{\boldsymbol{s}}}_{\mathit{t}}} \cdot {{\mathit{\boldsymbol{F}}}_{\mathit{t}}}\text{+}\mathit{B}_{\mathit{t}}^{ \Delta \mathit{s}}{{\mathit{\boldsymbol{s}}}_{\mathit{t}}} \cdot \Delta {{\mathit{\boldsymbol{s}}}_{\mathit{t}}}\text{+}\mathit{B}_{\mathit{t}}^{ \Delta \mathit{s}}{{\text{(}\nabla \cdot {{\mathit{\boldsymbol{s}}}_{\mathit{t}}}\text{)}}^{\text{2}}} \} \text{ , } \\ \end{align} $ | (5) |
式中:ρ, τ, j, s, T, J, F为Skyrme力的各个密度,相关定义见文献[20],各项前面的系数与ti, xj(i, j=0, 1, 2, 3), to, te和W0的关系见文献[27]。
本文采用不包含张量力的SLy5[28]和包含张量力的SLy5t[28], T22, T26, T44[29]总共5组Skyrme参数,研究16O+40Ca反应中的张量力效应,TDHF方程的计算是在没有任何对称性的三维数值格点上进行,格点的间隔是1.0 fm。首先由Hartree-Fock方程求解16O和40Ca的基态波函数,所用数值盒子大小为24 fm×24 fm×24 fm;在得到16O和40Ca的基态波函数之后,采用TDHF方程做16O+40Ca的动力学计算,动力学计算所用数值盒子大小为42 fm×24 fm×36 fm, 时间演化的步长为Δt=0.2 fm/c, 初始时刻弹靶核相对距离为28 fm。
2 张量力对熔合窗口的影响文献[20]研究张量力对16O+16O反应熔合阈值的影响,但是没有讨论张量力对动力学反应中熔合窗口的影响。由于熔合窗口的大小取决于高能熔合阈值与低能熔合阈值的差值,而对于中轻核反应体系,低能熔合阈值等于库仑位垒的高度。
2.1 库仑位垒首先采用冻结密度近似的方法[30]研究库仑位垒,该方法的主要思想是将动力学过程弹靶核的密度冻结在基态,在弹靶核相距为R时,由体系的总能量减去弹靶核各自的基态能量,从而得到两核之间的冻结近似势[31],其计算公式为
| $ {{\mathit{V}}^{\text{FD}}}\left( \mathit{R} \right)\text{=}\mathit{E}\left[ {{\mathit{\rho }}_{\text{P+T}}} \right]\left( \mathit{R} \right)\text{-}\mathit{E}\left[ {{\mathit{\rho }}_{\text{T}}} \right]\text{-}\mathit{E}\left[ {{\mathit{\rho }}_{\text{P}}} \right]\text{, } $ | (6) |
式中:ρP+T=ρP+ρT是弹靶核整个体系的总密度;E为体系Skyrme能量密度泛函,具体形式见式(5)。
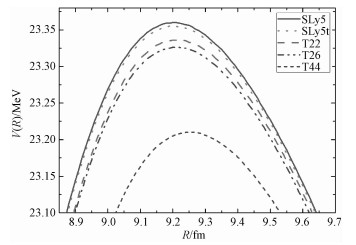
利用SLy5, SLy5t, T22, T26, T44这5组Skyrme参数,采用冻结密度近似方法,计算16O+40Ca体系弹靶核之间库仑位垒的高度与位置,计算精度为0.01 fm,计算结果见图 1和表 1。
|
Download:
|
| 图 1 相互作用势V(R) Fig. 1 Interaction potential V(R) | |
|
|
表 1 库仑位垒的高度V与位置R Table 1 Height V and location R of Coulomb barrier |
从表 1的结果可以看出,SLy5和SLy5t参数得出的库仑位垒高度和位置相同,这是由于张量力对自旋饱和核16O与40Ca的基态性质没有影响;而T22,T26,T44参数的库仑位垒高度和位置计算结果存在很小的差异,该差异是由于这3套Skyrme参数非张量力部分耦合常数的不同而引起的。图 1具体展示5组参数的相互作用势V与两核相对距离R关系的曲线。
综上可知,张量力对自旋饱和16O+40Ca体系的库仑位垒的位置与高度没有影响。
2.2 高能熔合阈值采用SLy5, SLy5t, T22, T26, T44这5组参数系统研究16O+40Ca体系的高能熔合阈值。高能熔合阈值的定义是:在对心碰撞(碰撞参数等于零)情况下,使得体系能够熔合时的最大质心系能量。在我们的研究中计算精度为1 MeV,计算结果见表 2。
|
|
表 2 高能熔合阈值 Table 2 The upper fusion threshold energy |
由表 2可知SLy5t和T26参数使得高能熔合阈值显著升高;而T22和T44参数使得高能熔合阈值降低。由文献[29]可知T26和T44参数的同位旋标量耦合常数是相同的,都等于120 MeV·fm5,同位旋矢量耦合常数分别为120和0 MeV·fm5,对比表 2中T26和T44的高能熔合阈值,可以得到同位旋矢量张量项以及平均场重排使高能熔合阈值升高;T22和T44参数的同位旋矢量耦合常数是相同的,都等于0 MeV·fm5,同位旋标量耦合常数分别为0和120 MeV·fm5,对比表 2中T22和T44的高能熔合阈值,可以得到同位旋标量张量项以及平均场重排使高能熔合阈值升高。由此可知张量力对高能熔合阈值有显著影响。在文献[22]中,发现16O+16O体系中张量力对高能熔合阈值的影响也不可忽略。
综合张量力对低能熔合阈值和高能熔合阈值的影响,在16O+40Ca体系中,张量力主要通过对高能熔合阈值的影响,从而使得熔合窗口的大小发生变化。其中SLy5t和T26参数使得熔合窗口变大,而T22和T44参数使得熔合窗口变小。
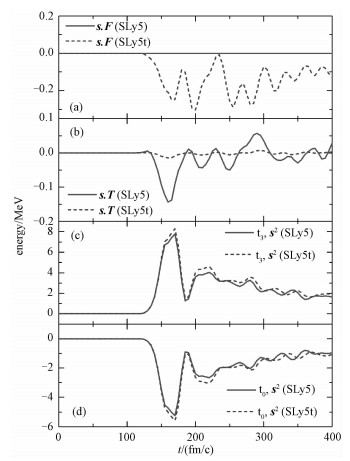
3 张量力对Skyrme能量密度泛函中各项能量贡献的影响为研究张量力对Skyrme能量密度泛函中各项能量贡献的影响,选取SLy5和SLy5t参数,质心系下的体系能量Ec.m.=170 MeV,碰撞参数b=0 fm,对16O+40Ca体系Skyrme能量密度泛函中各项能量的贡献进行研究,奇时间项部分的能量贡献的计算结果见图 2。对比表 2中16O+40Ca体系SLy5和SLy5t参数下高能熔合阈值可知,在Ec.m.=170 MeV的对心碰撞,发生的是深度非弹碰撞。由图 2发现,在动力学的初始时刻,奇时间各项的能量贡献都为零,因为初始时刻体现的弹靶核的基态性质,奇时间项对偶偶核的基态没有影响,随着弹核和靶核逐渐靠近,各项能能量贡献逐渐出现差异,因为s2项仅出现在中心力场中,张量力部分没有s2项,所以在SLy5和SLy5t参数下,s2项的能量贡献差异来自于平均场的重排;由于SLy5参数中不包含张量力部分的s.F项,因此整个动力学过程中,SLy5参数计算的s.F项能量贡献为零;而s.T项既有中心力场部分,又有张量力部分,从s.T项的能量贡献知道,张量力抵消了一部分来自中心力场s.T项的能量贡献。
|
Download:
|
| 图 2 奇时间项的能量贡献 Fig. 2 Energy contribution of time-odd terms | |
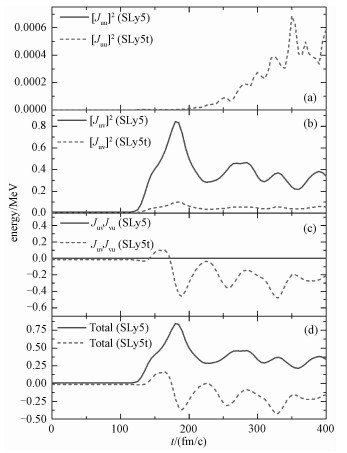
图 3展示的是来自J2项中各个分项能量贡献以及总能量贡献。由于SLy5参数中没有张量力项,只包含有Juv2项,因此Juu2项贡献和JuvJvu项贡献分别为零。从图 3(d)可以看到,由于张量力的引入,J2项的总能量贡献符号是相反的,其原因是SLy5t参数中所包含的J2项既有中心力场部分,又有张量力部分,中心力场部分J2项的耦合常数是正的,张量力部分J2项的耦合常数是负的,即这两部分的效应相反,并且对中心力场和张量力部分的J2项求和之后,总耦合常数为负值,从而使得SLy5t的J2项总能量贡献为负值。
|
Download:
|
| 图 3 J2项的能量贡献 Fig. 3 Total energy contribution of J2 term | |
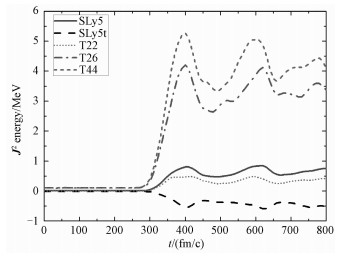
以上研究是在16O+40Ca体系发生深度非弹碰撞下的结果,我们还研究16O+40Ca体系发生熔合时的情况,当质心系能量Ec.m.=46.5 MeV, 碰撞参数b=5.0 fm时会发生熔合,在该反应中,不同Skyrme参数下J2项的总能量贡献见图 4。
|
Download:
|
| 图 4 不同力J2项的总能量贡献 Fig. 4 Total energy contribution of J2 term for different forces | |
在图 4中,动力学的初始时刻,所有参数的J2项的总能量贡献都近似为零,当进入碰撞阶段,J2项的总能量贡献都不为零,而且只有SLy5t的J2项的总能量贡献是负值,其他4组参数的J2项的总能量贡献都是正值。由文献[29]可知,T26和T44参数的同位旋标量耦合常数是相同的,都等于120 MeV·fm5,同位旋矢量耦合常数分别为120和0 MeV·fm5,对比图 4中T26和T44的J2项的总能量贡献,可以得到同位旋矢量张量项以及平均场重排使J2项的总能量贡献减小;T22和T44参数的同位旋矢量耦合常数是相同的,都等于0 MeV· fm5,同位旋标量耦合常数分别为0和120 MeV·fm5,对比图 4中T22和T44的J2项的总能量贡献,可以得到同位旋标量张量项以及平均场重排使J2项的总能量贡献增大。而且包含张量力的4组参数的能量贡献大小与不包含张量力SLy5参数的能量贡献大小都不同。以上这些结果表明在重离子碰撞过程中,张量力对Skyrme能量密度泛函能量贡献的影响是不可忽略的。
4 小结与展望通过以上张量力对16O+40Ca体系库仑位垒、高能熔合阈值以及Skyrme能量密度泛函能量贡献影响的研究发现,张量力对自旋饱和体系16O+40Ca的库仑位垒没有影响;张量力对高能熔合阈值影响比较显著,同位旋标量、同位旋矢量张量项和平均场重排使得高能熔合阈值升高,其中SLy5t和T26参数使得熔合窗口变大,而T22和T44参数使得熔合窗口变小;在重离子碰撞中,张量力使Skyrme能量密度泛函中的各项能量贡献发生变化,同位旋标量张量项以及平均场重排使自旋流赝张量项的总能量贡献增大, 同位旋矢量张量项以及平均场重排使自旋流赝张量项的总能量贡献减小。综上所述,张量力对16O+40Ca体系重离子碰撞过程的影响是不可忽略的。
有关张量力在核反应的效应,未来还有很多值得继续去研究的课题,比如:张量力对熔合截面和动力学库仑位垒的影响, 张量力对核反应中动力学耗散影响等等。
本文中的计算是在国家超级计算天津中心计算资源的支持下完成的。
| [1] |
Dirac P A. Note on exchange phenomena in the Thomas atom[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1930, 26(3):376–385.
DOI:10.1017/S0305004100016108 |
| [2] |
Guo L, Maruhn J A, Reinhard P G, et al. Conservation properties in the time-dependent Hartree Fock theory[J]. Phys Rev C, 2008, 77(4):041301.
|
| [3] |
Umar A S, Oberacker V E, Maruhn J A, et al. Entrance channel dynamics of hot and cold fusion reactions leading to superheavy elements[J]. Phys Rev C, 2010, 81(6):064607.
DOI:10.1103/PhysRevC.81.064607 |
| [4] |
Guo L, Nakatsukasa. Time-dependent Hartree-Fock studies of the dynamical fusion threshold[C]//Ershov S, Shneydman T, Vdovin A, et al. International Conference on Nuclear Structure and Related Topics. London: EDP Sciences Press, 2012: 09003.
|
| [5] |
Maruhn J A, Reinhard P G, Stevenson P D, et al. Spin-excitation mechanisms in Skyrme-force time-dependent Hartree-Fock calculations[J]. Phys Rev C, 2006, 74(2):027601.
DOI:10.1103/PhysRevC.74.027601 |
| [6] |
Guo L, Maruhn J A, Reinhard P G. Boost-invariant mean field approximation and the nuclear Landau-Zener effect[J]. Phys Rev C, 2007, 76(1):014601.
|
| [7] |
Simenel C. Particle-number fluctuations and correlations in transfer reactions obtained using the Balian-Vénéroni variational principle[J]. Phys Rev Lett, 2011, 106(11):112502.
DOI:10.1103/PhysRevLett.106.112502 |
| [8] |
Dai G F, Guo L, Zhao E G, et al. Dissipation dynamics and spin-orbit force in time-dependent Hartree-Fock theory[J]. Phys Rev C, 2014, 90(4):044609.
DOI:10.1103/PhysRevC.90.044609 |
| [9] |
Simenel C, Chomaz P, France D. Quantum calculation of the Dipole excitation in fusion reactions[J]. Phys Rev Lett, 2001, 86(14):2971.
DOI:10.1103/PhysRevLett.86.2971 |
| [10] |
Reinhard P G, Guo L, Maruhn J A. Nuclear giant resonances and linear response[J]. Eur Phys J A, 2007, 32:19–23.
DOI:10.1140/epja/i2007-10366-9 |
| [11] |
Wakhle A, Simenel C, Hinde D, et al. Interplay between quantum shells and orientation in quasifission[J]. Phys Rev Lett, 2014, 113(18):182502.
DOI:10.1103/PhysRevLett.113.182502 |
| [12] |
Suckling E B. Nuclear structure and dynamics from the fully unrestricted Skyrme-Hartree-Fock model[D]. Guildford: University of Surrey, 2011.
|
| [13] |
Colò G, Sagawa H, Fracasso S, et al. Spin orbit splitting and the tensor component of the Skyrme interaction[J]. Phys Lett B, 2007, 646(5):227–231.
|
| [14] |
Li Z Y, Wang Y Z, Yu G L, et al. Tensor force effect on proton shell structure in neutron-rich Ca isotopes[J]. Sci China-Phys Mech Astron, 2013, 56(9):1719–1729.
DOI:10.1007/s11433-013-5143-0 |
| [15] |
Cao L G, Colò G, Sagawa H, et al. Effects of the tensor force on the multipole response in finite nuclei[J]. Phys Rev C, 2009, 80(6):064304.
DOI:10.1103/PhysRevC.80.064304 |
| [16] |
Grasso M. Magicity of the 52Ca and 54Ca isotopes and tensor contribution within a mean-field approach[J]. Phys Rev C, 2014, 89(3):034316.
DOI:10.1103/PhysRevC.89.034316 |
| [17] |
Otsuka T, Fujimoto R, Utsuno Y, et al. Magic numbers in exotic nuclei and spin-isospin properties of the NN interaction[J]. Phys Rev Lett, 2001, 87(8):082502.
DOI:10.1103/PhysRevLett.87.082502 |
| [18] |
Otsuka T, Matsuo T, Abe D. Meanfield with tensor force and shell structure of exotic nuclei[J]. Phys Rev Lett, 2006, 97(16):162501.
DOI:10.1103/PhysRevLett.97.162501 |
| [19] |
Otsuka T, Suzuki T, Fujimoto R, et al. Evolution of nuclear shells due to the tensor force[J]. Phys Rev Lett, 2005, 95(23):232502.
DOI:10.1103/PhysRevLett.95.232502 |
| [20] |
Stevenson P D, Suckling E B, Fracasso S, et al. Skyrme tensor force in heavy ion collisions[J]. Phys Rev C, 2016, 93(5):054617.
DOI:10.1103/PhysRevC.93.054617 |
| [21] |
Dai G F, Guo L, Zhao E G, et al. Effect of tensor force on dissipation dynamics in time-dependent Hartree-Fock theory[J]. Sci China-Phys Mech Astron, 2014, 57(9):1618–1622.
DOI:10.1007/s11433-014-5536-8 |
| [22] |
Skyrme T R M. The nuclear surface[J]. Philos Mag, 1956, 1(11):1043–1054.
DOI:10.1080/14786435608238186 |
| [23] |
Skyrme T R M. The effective nuclear potential[J]. Nuclear Physics, 1959, 9(4):615–634.
|
| [24] |
Skyrme T R M. The spin-orbit interaction in nuclei[J]. Nuclear Physics, 1958, 9(4):635–640.
DOI:10.1016/0029-5582(58)90346-8 |
| [25] |
Bell J S, Skyrme T R M. The nuclear spin-orbit coupling[J]. Phil Mag, 1956, 1(11):1055–1068.
DOI:10.1080/14786435608238187 |
| [26] |
Bartel J, Quentin P, Brack M, et al. Towards a better parametrisation of Skyrme-like effective forces:a critical study of the SkM force[J]. Nuclear Physics A, 1982, 386(1):79–100.
DOI:10.1016/0375-9474(82)90403-1 |
| [27] |
Kim K, Otsuka K, Bonche P. Three-dimensional TDHF calculations for reactions of unstable nuclei[J]. J Phys G, 1997, 23:1273–1276.
|
| [28] |
Chabanat E, Bonche P, Haensel P, et al. A Skyrme parametrization from subnuclear to neutron star densities Part Ⅱ. Nuclei far from stabilities[J]. Nuclear Physics A, 1998, 635(2):231–256.
|
| [29] |
Lesinski T, Bender M, Bennaceur K, et al. Tensor part of the Skyrme energy density functional: spherical potentials in the synthesis of the heaviest nuclei[J]. Eurnuclei[J]. Phys Rev C, 2007, 76(1): 014312.
|
| [30] |
Denisov V Y, Nörenberg W. Entrance channel Phys J A-Hadrons and Nuclei, 2002, 15(3): 375-388.
|
| [31] |
Washiyama K, Lacroix D. Energy dependence of the nucleus-nucleus potential close to the Coulomb barrier[J]. Phys Rev C, 2008, 78(2):024610.
DOI:10.1103/PhysRevC.78.024610 |
| [32] |
Vaz L Z, Alexander J M, Satchler G R. Fusion barriers, empirical and theoretical:evidence for dynamic deformation in subbarrier fusion[J]. Phys Rep, 1981, 69(5):373–399.
DOI:10.1016/0370-1573(81)90094-6 |
 2018, Vol. 35
2018, Vol. 35 


