2. 中国科学院工程热物理研究所, 北京 100190
2. Institute of Engineering Thermal Physics, Chinese Academy of Sciences, Beijing 100190, China
在一个密闭的充满工质的腔体中,对其一侧边界施加一个快速的热扰动(如迅速的温度上升),在该侧壁面处会形成极薄的热边界层,由于热边界层附近的工质存在惯性,热边界层的膨胀受到抑制,此时会造成瞬时的局部压力升高,产生压力波。压力波以接近声音的速度在腔体中传播,并将能量传递给工质,大大缩短系统达到热平衡的时间。这种快速的传热现象即为活塞效应(piston effect,简称PE效应)[1-2]。活塞效应是热声效应在时间上的累积,本质上是一种热声效应,通常发生在可压缩流体中,是热过程与机械过程耦合的结果。在传统的导热对流传热模式中,若热扩散由于失重、低温等原因受到抑制,则活塞效应就会成为一种主要的传热机制[3]。
由于活塞效应的实验研究需要排除自然对流的干扰,实验实施存在很大困难,因此需要通过数值模拟方法研究[4]。目前存在两种计算模型对活塞效应进行数值求解:1)直接求解可压缩流体控制方程组,即流体力学模型;2)对流体力学模型进行化简,得到的热力学模型。前者偏重机理研究,计算量大,耗时长;后者更注重宏观传热效果,计算速度相对较快。Zappoli等[5]通过求解完全可压缩流体方程模拟失重条件下二氧化碳临界点附近的快速传热过程,并将这种现象称为活塞效应;Farouk等[1]通过求解非稳态可压缩流体的N-S方程并改变诱发热声波的方式,指出脉冲加热的方式会产生更强烈的压力波动;李玉华等[6-7]通过求解可压缩流体动力学控制方程研究液体中热声效应的传热机理。毛宇飞和郭烈锦[4]通过数值求解活塞效应热力学模型,研究超临界水中的活塞效应传热现象,并将绝热指数作为衡量活塞效应强度的参数;Miura等[8]采用干涉法测出微小扰动下二氧化碳中的密度变化,并理论分析活塞效应中声波的传递过程;Lin和Farouk[9]实验研究超临界二氧化碳中热声效应的产生、传递、延迟过程,并通过数值求解可压缩流体控制方程模拟实验过程,实验结果和理论计算吻合。
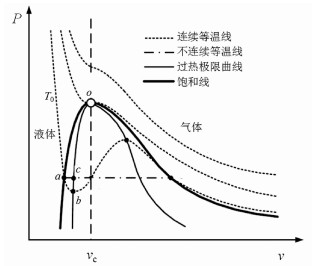
目前,国内外关于活塞效应的研究主要集中在气体区、液体区、超临界区及临界点附近[3],过热液体中的研究并未出现。过热液体是一种典型的亚稳态,在传统热管、大充液率虹吸管、蒸发器的启动阶段等比较常见,而文献中鲜有对其传热机理的分析[10]。Nichele等[11]根据分子动力学模拟出物质的P-v图,如图 1所示:a、b在同一条等温线上,b点是a点对应温度下的拐点(即a点的过减压态),c点是a点相同压力下的过热区温度极点,o点是气液临界点,饱和液体线oa和旋节线ob之间的区域为过热液体区。
|
Download:
|
| 图 1 过热液体亚稳态相图[11] Fig. 1 Superheat liquid meta-stable diagram | |
本文以一维密闭腔体中可压缩流体R134a为研究对象。首先,根据可压缩流体Navier-Stokes方程建立过热液体中活塞效应的流体力学模型,模拟过热液体中活塞效应的传热过程;然后,将流体力学模型进行简化,得到优化的热力学模型,根据热力学模型计算出活塞效应的当量热导率,并与工质自身热导率对比,定量得到活塞效应对传热的贡献;最后,采用热力学模型,通过改变液体相对过热比,进一步研究过热程度对活塞效应的影响。
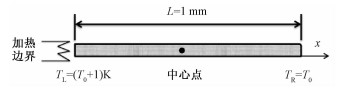
1 计算区域及数学模型计算区域如图 2所示,在长度为L的一维密闭区域中,充满过热液体R134a。其中,L为模型长度,P0为初始压力,T0为初始温度,TL为左边界温度,TR为右边界温度。当时间t=0 s时,TL=TR=T0;当t>0 s时,左边界温度从T0阶跃至((T0+1) K),右边界温度保持T0不变。定义相对过热比s=v/vb,s越大,代表过热程度越大,当液体处于饱和状态时,s=vsl/vb。其中:v为液体初始状态的比体积,vsl为相应温度下的饱和液体的比体积,vb为过热液体相同温度下拐点处的比体积。当液体处于相应温度下的拐点时,s=1。
|
Download:
|
| 图 2 计算区域 Fig. 2 Calculation domain | |
过热液体的非稳态可压缩流体问题可以用质量、动量、能量守恒控制方程组来描述[3]:
| $ \frac{\partial \mathit{\rho }}{\partial \mathit{t}}\text{+}\nabla \text{ } \cdot \text{ (}\mathit{\rho }\mathit{\boldsymbol{v}}\text{)=0}, $ | (1) |
| $ \begin{align} &\mathit{\rho }\left[ \frac{\partial \mathit{\boldsymbol{v}}}{\partial \mathit{t}}\text{+ (}\mathit{\boldsymbol{v}}\text{ } \cdot \text{ grad)}\mathit{\boldsymbol{v}} \right]\text{=-grad}\mathit{P}\text{+}{{\mathit{\eta }}_{\text{s}}}\text{ } \Delta \text{ }\mathit{\boldsymbol{v}}\text{+} \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( \frac{\text{1}}{3}{{\mathit{\eta }}_{\text{s}}}\text{+}{{\mathit{\eta }}_{\text{b}}} \right)\text{graddiv}\mathit{\boldsymbol{v}}\text{, } \\ \end{align} $ | (2) |
| $ \frac{\partial \mathit{E}}{\partial \mathit{t}}\text{+}\mathit{\boldsymbol{v}}\text{ } \cdot \text{ grad } ~ \text{ }\left( \mathit{E}\text{+}\mathit{P} \right)\text{=div(}\mathit{\lambda }\text{grad}\mathit{T}\text{)+}\mathit{\Phi }\text{, } $ | (3) |
式中:ηs为剪切黏度,ηb为体积黏度, Φ为黏性耗散项。能量方程(3)的左边可以转化为
| $ \begin{align} &\frac{\partial \mathit{E}}{\partial \mathit{t}}\text{+}\mathit{\boldsymbol{v}}\text{ } \cdot \text{ grad } ~ \text{ }\left( \mathit{E}\text{+}\mathit{P} \right)\text{= }\mathit{\rho T}\left[ \left( \frac{\partial \mathit{s}}{\partial \mathit{t}} \right)\text{+}\mathit{\boldsymbol{v}}\text{ } \cdot \text{ grad}\mathit{s} \right] \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{=}\mathit{\rho T}\frac{\text{D}\mathit{s}}{\text{D}\mathit{t}}\text{.} \\ \end{align} $ | (4) |
结合流体力学物质导数:D/Dt=∂/∂t+ν·grad, 并将方程(4)代入方程(3)得到能量方程
| $ \begin{align} &\mathit{\rho }{{\mathit{C}}_{\text{p}}}\frac{\mathit{DT}}{\mathit{Dt}}\text{=}\nabla \text{ } \cdot \text{ }\left( \mathit{\lambda }\nabla \mathit{T} \right)\text{+}\mathit{\Phi }\text{+}\mathit{\rho }\left( {{\mathit{C}}_{\text{p}}}\text{-}{{\mathit{C}}_{\text{v}}} \right)\frac{{{\mathit{\kappa }}_{\text{T}}}}{{{\mathit{\alpha }}_{\text{v}}}}\frac{\text{D}\mathit{P}}{\text{D}\mathit{t}} \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \text{=}\nabla \text{ } \cdot \text{ (}\mathit{\lambda }\nabla \mathit{T}\text{)+}\mathit{\Phi }\text{+}\mathit{T}{{\mathit{\alpha }}_{\text{v}}}\frac{\text{D}\mathit{P}}{\text{D}\mathit{t}}\text{, } \\ \end{align} $ | (5) |
式中:αv为体积膨胀系数,ΚT为等温压缩率。当不考虑重力并抵消黏性耗散时,方程(5)简化为
| $ \mathit{\rho }{{\mathit{C}}_{\text{p}}}\frac{\partial \mathit{T}}{\partial \mathit{t}}\text{=}\nabla \text{ } \cdot \text{ (}\mathit{\lambda }\nabla \mathit{T}\text{)+}\mathit{T}{{\mathit{\alpha }}_{\text{v}}}\frac{\partial \mathit{P}}{\partial \mathit{t}}\text{, } $ | (6) |
式中: ρCp(∂T/∂t)为传递的总能量,∇·(λ∇T)为热扩散项,Tαv(∂P/∂t)为PE效应项。在不可压缩流体中,Cp=Cv,PE项降为0,方程(6)就转化为经典的导热对流能量方程。
方程(1)、(2)和(6)组成活塞效应的流体力学模型。
在活塞效应作用下, 声音传播的时间尺度ta、热扩散的时间尺度td表达式如下
| $ {{\mathit{t}}_{\text{a}}}\text{=}\mathit{L}\text{/}{{\mathit{a}}_{\text{0}}}\text{, }\ {{\mathit{t}}_{\text{d}}}\text{=}{{\mathit{L}}^{\text{2}}}\text{/}\mathit{D}\text{.} $ | (7) |
式中: a0表示声音在工质中的传播速度,D表示热扩散率。由于ta远小于td,因此可以直接从能量方程出发导出简化的数学模型。这里假设流体运动被忽略,并且系统压力只随时间变化[12],则得到活塞效应的热力学模型。文献中通常采用热力学方程得到压力变化方程
| $ \frac{\partial \mathit{P}}{\partial \mathit{t}}\text{=}\frac{\int_{\mathit{V}}{\mathit{\rho }{{\mathit{\alpha }}_{\text{v}}}\partial \mathit{T}\text{/}\partial \mathit{t}\text{ } \cdot \text{ d}\mathit{V}}}{\int_{\mathit{V}}{\mathit{\rho }{{\mathit{\kappa }}_{\text{T}}}\text{d}\mathit{V}}}\text{, } $ | (8) |
式中: αv为体积膨胀系数,κT为等温压缩率。由于式(8)不能充分保证能量守恒,因此,为了使热力学模型能够更好地保证能量守恒,本文做出改进:由能量守恒方程(3)转化得到内能变化方程(9),再结合实际流体状态方程[13] (10)得到压力值。
| $ \int_{\mathit{V}}{\frac{\partial \mathit{U}}{\partial \mathit{t}}\text{d}\mathit{V}}\text{=}\int_{\mathit{S}}{\mathit{\vec{q}}\text{ } \cdot \text{ }\mathit{\vec{n}}\text{d}\mathit{S}}\text{, } $ | (9) |
| $ \frac{\text{d}\mathit{P}}{\text{d}\mathit{t}}\text{=}\frac{\text{1}}{\mathit{\rho }{{\mathit{\kappa }}_{\mathit{T}}}}\frac{\text{d}\mathit{\rho }}{\text{d}\mathit{t}}\text{+}\frac{{{\mathit{\alpha }}_{\text{v}}}}{{{\mathit{\kappa }}_{\mathit{T}}}}\frac{\text{d}\mathit{T}}{\text{d}\mathit{t}}\text{.} $ | (10) |
方程(9)中热流密度计算公式如下(其中λ为热导率):
| $ {{\mathit{q}}_{\mathit{x}}}\text{=-}\mathit{\lambda }\frac{\partial \mathit{T}}{\partial \mathit{x}}\text{.} $ | (11) |
方程(9)、(10)即为本文所采用的活塞效应热力学模型。在以上两种模型的计算过程中,时间项采用2阶精度MacCormack显式格式,扩散项采用中心差分格式,PE效应项采用FCT格式,并对控制方程(6)采用有限体积法进行离散;非均匀网格数目设置为1 000,并经过网格无关性验证。迭代过程中,时间步长自动调整。R134a物性值采用美国物理研究所和化学学会于1994年公布的R134国际物性标准公式[14]计算得出,R134a过热液体区的拐点参数采用范德瓦尔方程计算得出。
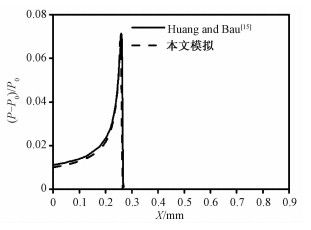
为验证本计算方法的可靠性,本文采用流体力学模型计算理想气体中的热声波,并将计算结果与Huang和Bau[15]的计算结果进行对比(图 3),结果显示,在相同的初始条件下(T0=300 K,P0=1.0E5 Pa,阶跃温度为1 K的脉冲加热),两者高度吻合。
|
Download:
|
| 图 3 理想气体中热声波计算结果对比 Fig. 3 Calculation results for thermo-acoustic wave in ideal gas | |
模型长度L=1 mm, 工质初始温度为T0=350 K,初始相对过热比s=0.93,此时拐点处参数为:Ts=350 K,Ps=2.446 MPa,vs=1.68E-4 m3/kg,工质初始状态在图 1中线ab之间。当时间t>0 s时,对左边界进行阶跃温度为1 K的等温加热,右边界温度保持不变。通过采用流体力学方法计算,计算结果如图 4所示,其中,无量纲时间参数t*=t/ta。

|
Download:
|
| 图 4 活塞效应的传热过程 Fig. 4 Heat transfer process of PE | |
图 4(a)所示为压力波在不同时刻的空间位置分布。当对左边界施加温度为1 K的阶跃加热时,由于左边界温度突然上升,在与左边界紧邻的流体处会产生一个热边界层,热边界层膨胀,挤压相邻流体,产生局部的压力上升,形成压力波,压力波在热边界层的驱动下以声速向+x方向运动;当t*=0.01时,在热边界层附近的一个很小的区域内,工质压力升高约600 Pa,而其余位置压力保持不变;当t*=0.6时,压力波到达x=0.6 mm附近,随后压力波到达右边界处并被反射,沿x轴负方向传播,像“活塞”一样在腔体中往复运动;t*=1.1和t*=1.3是压力波在右边界处反射之后的空间分布曲线,从图中可以看出,压力波传播方向的前端陡峭,尾部相对缓和。
图 4(b)所示为中心点处的压力随时间t*的变化过程。无论是左边界产生的压力波,还是右边界反射的压力波都会引起中心点处压力瞬时升高。
图 4(c)所示为不同时刻系统温度的空间分布。在t*=0.1时,压力波使x=0.10 mm附近处工质产生5 mK的瞬时温升,而压力波没有经过之处温度并未发生变化;当t*=0.6时,x=0.6 mm附近的温度开始上升,与压力的空间分布一致,温度随着压力波产生周期性变化。从控制方程(6)可以看出,热能与机械能相互耦合,压力波将携带的机械能转化为流体内能。
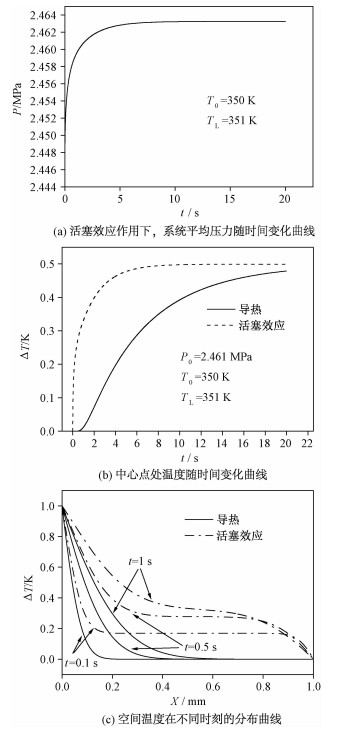
2.2 活塞效应与导热传热过程比较为研究过热液体中活塞效应对传热的贡献,本节采用热力学模型对过热液体进行计算。计算物理模型、工质初始及边界条件同2.1节,活塞效应与导热传热的计算时间均为20 s, 计算结果如图 5所示。
|
Download:
|
| 图 5 活塞效应与单纯导热对比 Fig. 5 Comparison between piston effect and pure heat conduction | |
图 5(a)所示为活塞效应作用下系统内平均压力随时间变化情况。系统内平均压力随时间迅速升高到稳定值,而单纯导热过程中系统内部无明显压力变化。由于导热是以热扩散为传热动力,活塞效应是以热边界层产生的压力波为传热动力,而热扩散速度明显小于压力波传递速度,因此与导热相比,活塞效应可以使系统更快地实现热平衡。
图 5(b)为两种传热方式下,中心点处温度随时间的变化曲线。在活塞效应作用下,在t=5 s左右,中心点处温度已达到0.5 K,已基本实现热平衡,而单纯导热方式下,t=20 s时尚未达到热平衡。
图 5(c)所示为两种传热方式下不同时刻的温度空间分布图,温度分布趋势与文献[13]相似。与单纯导热相比,在相同的时刻,活塞效应作用下系统内温度更高,工质主流温度分布更均匀,并且随着时间的推移,热边界层变厚,活塞效应逐渐变弱。
2.3 活塞效应方式下的当量热导率为了定量比较两种传热方式下的传热系数,本文根据方程(12)计算出活塞效应的当量热导率λe,其中,qw2为右边界处热流密度。
| $ {{\mathit{\lambda }}_{\text{e}}}\left( \mathit{t} \right)\text{=}\frac{{{\mathit{q}}_{\text{w2}}}\text{ } \cdot \text{ }\mathit{L}}{{{\mathit{T}}_{\text{L}}}\text{-}{{\mathit{T}}_{\text{0}}}}\text{.} $ | (12) |
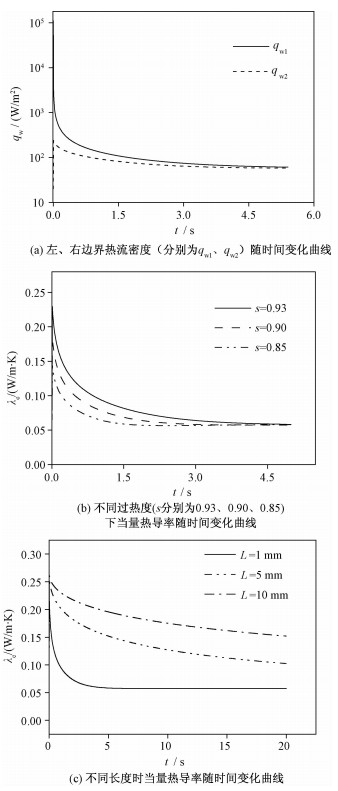
活塞效应的计算条件同2.2节,图 6(a)是活塞效应传热方式下左、右边界处热流密度(qw1、qw2)随时间的变化曲线。左右边界热流密度计算公式如式(11)所示。
|
Download:
|
| 图 6 各参量对活塞效应强度的影响 Fig. 6 Influences of various parameters on PE | |
随着时间的推移,左右边界处热流密度趋于一致。图 6(b)中实线(s=0.93)为该条件下,当量热导率随时间的变化曲线,如图所示,当量热导率最大值出现在施加温度阶跃的开始阶段,其值λe≈0.24 W/(m·K)。从文献[16-17]查到R134a的导热系数λ≈0.057~0.060 W/(m·K),因此,活塞效应当量热导率是工质自身热导率的3倍多,并且在系统趋于热平衡时,当量热导率才接近工质的实际热导率。为保证计算过程中工质状态始终在过热液体区,本文采用阶跃温度为1 K的小温差加热方式,所以,与文献[14]计算结果相比,当量热导率要小一些。
为进一步研究工质初始过热状态对活塞效应强度的影响,在其他条件相同的情况下,本文对比3种不同的初始相对过热比:s=0.93,s=0.90,s=0.85。图 6(b)所示为3种过热度下当量热导率随时间变化曲线,在短时间内,当量热导率随过热度的增大而变大,这与等温线拐点附近流体剧烈变化的物性值有关,在拐点处,热膨胀系数趋于无穷大,极小的热扰动会产生很大的压力波动。图 6(c)所示为不同长度下当量热导率随时间的变化曲线,在同一时刻,长度L越大,当量热导率越大,而L越大,系统的当量热导率减小得越慢,这说明在较长的距离内,活塞效应仍可以起到强化传热的作用。
3 结论通过对过热液体R134a中活塞效应的数值模拟,本文得出以下结论:
1) 活塞效应不仅存在于临界点附近的流体中,而且也存在于过热液体中。由于过热液体具有较大的热膨胀系数和较小的等温压缩率,所以,在加热边界处的热边界层内产生压力波,能量以压力波为载体在流体与左右边界之间传递,使系统快速实现热平衡;活塞效应传热过程熵产极小,可以认为是绝热压缩过程,是不同于传统的导热、对流、辐射的热机耦合传热机制。
2) 由于声学时间尺度远远小于扩散时间尺度,所以在过热液体中,活塞效应的当量热导率明显大于单纯导热,并随着系统趋于热平衡而减弱,最终趋于工质自身热导率。
3) 通过改变计算的初始相对过热比,发现在一定范围内,活塞效应强度与工质初始过热程度呈正相关,即在小温差加热范围内,活塞效应强度随着相对过热比的增大而增强,并且在较长的距离内,活塞效应也可以起到强化传热的作用。
| [1] |
Farouk B, Oran E S, Fusegi T. Numerical study of thermoacoustic waves in an enclosure[J]. AIP Physics of fluids, 2000, 12(5):1052–1061.
DOI:10.1063/1.870360 |
| [2] |
Hasan N, Farouk B. Fast heating induced thermoacoustic waves in supercritical fluids:experimental and numerical studies[J]. Journal of Heat Transfer, 2013, 135(8):1701–1712.
|
| [3] |
Shen B, Zhang P. An overview of heat transfer near the liquid-gas critical point under the influence of the piston effect:phenomena and theory[J]. International Journal of Thermal Sciences, 2013, 71:1–19.
DOI:10.1016/j.ijthermalsci.2013.04.010 |
| [4] |
毛宇飞, 郭烈锦. 超临界水活塞效应传热现象的数值模拟[J]. 自然科学进展, 2006, 16(4):457–462.
|
| [5] |
Zappoli B, Beysen D, Guenoun P. Anomalies of heat transport in near critical fluids under weightlessness[J]. Advances in Space Research, 1991, 11(7):269–276.
DOI:10.1016/0273-1177(91)90295-U |
| [6] |
李玉华, 占丽媛, 姜玉雁, 等. 液相工质中热声效应数值模拟研究[J]. 工程热物理学报, 2014, 35(11):2274–2277.
|
| [7] |
占丽媛, 李玉华, 姜玉雁, 等. 密闭二维腔体内水中热声波的数值模拟[J]. 化工学报, 2014, 65(S1):32–38.
|
| [8] |
Miura Y, Yoshihara S, Ohnishi M. High-speed observation of the piston effect near the gas-liquid critical point[J]. Physical Review E, 2006, 74(1):010101.
DOI:10.1103/PhysRevE.74.010101 |
| [9] |
Lin Y, Farouk B. Experimental and numerical studies of thermally induced acoustic waves in an enclosure[J]. Journal of Thermophysics and Heat Transfer, 2008, 22(1):105–114.
DOI:10.2514/1.29776 |
| [10] |
刘杰, 李廷勋, 裴念强, 等. 两相冷却系统过热现象与启动温度关系分析[J]. 制冷学报, 2007, 28(6):23–28.
|
| [11] |
Nichele J, Alves S L B, Borges I. Equation of state for near critical argon obtained via molecular dynamics[J]. High Temperatyre High Pressure, 2014, 43(5):385–400.
|
| [12] |
Straub J, Eicher L, Haupt A. Dynamic temperature propagation in a pure fluid near its critical point observed under microgravity during the German Spacelab Mission D-2[J]. Physical Review E, 1995, 51(6):5556–5563.
DOI:10.1103/PhysRevE.51.5556 |
| [13] |
Nakano A, Shiraishi M. Piston effect in supercritical nitrogen around the pseudo-critical line[J]. International Communications in Heat and Mass Transfer, 2005, 32(9):1152–1164.
DOI:10.1016/j.icheatmasstransfer.2005.05.009 |
| [14] |
Tillner-Roth R, Baehr H D. An international standard formulation for the thermodynamic properties of 1, 1, 1, 2-tetrafluoroethane (HFC-134a) for temperatures from 170K to 455K and pressures up to 70MPa[J]. Journal of Physical and Chemical Reference Data, 1994, 23(5):657–729.
DOI:10.1063/1.555958 |
| [15] |
Huang Y, Bau H H. Thermoacoustic waves in a confine medium[J]. International Journal of Hear Mass Transfer, 1997, 40(2):407–419.
DOI:10.1016/0017-9310(96)00068-3 |
| [16] |
Gross U, Song Y W, Hahne E. Thermal conductivity of the new refrigerants R134a, R152a and R123 measured by the transient hot-wire method[J]. International Journal of Thermophysics, 1992, 13(6):957–983.
DOI:10.1007/BF01141209 |
| [17] |
Baginsky A V, Shipitsyna A S. Thermal conductivity and thermal diffusivity of the R134a refrigerant in the liquid state[J]. Thermophysics and Aeromechanics, 2009, 16(2):267–273.
DOI:10.1134/S0869864309020115 |
 2018, Vol. 35
2018, Vol. 35 


