极小曲面的研究一直是微分几何子流形研究领域中的一个重点, 通常对于极小曲面的研究, 会选取具有特殊性质的外围空间, 如空间形式、齐性空间等。而四元数射影空间是对称空间, 因此四元数射影空间中极小曲面的研究具有重要意义。但是因为四元数射影空间本身的结构比较复杂, 所以四元数射影空间中极小曲面的研究也颇为困难。

这些年来, 在国内外学者的研究下, 四元数射影空间中极小曲面的研究也取得了一些重要的研究成果。

由文献[1], 我们知道四元数射影空间$ \mathbb{H}$P¹与标准球面S⁴是等距同构的, 因此在微分同胚的意义下, $ \mathbb{H}$P¹中的极小曲面研究通常转化为对S⁴中极小曲面的研究。Bryant^[2]利用扭映射π:$ \mathbb{C}$P³→$ \mathbb{H}$P¹研究$ \mathbb{H}$P¹中的共形极小紧致曲面, 并且构造$ \mathbb{C}$P³中的水平全纯曲面。对于四元数射影空间$ \mathbb{H}$P²的研究也取得了很多成果。Aithal^[3]刻画从S²到$ \mathbb{H}$P²中的调和映射。Bahy-El-Dien和Wood^[4]构造四元数射影空间中的调和二维球面。注意到，在共形映射的意义下, 映射调和等价于映射极小^[5]。基于这些事实, He和Jiao^[6]给出$ \mathbb{H}$P²中线性满、全非分歧、常曲率共形极小二维球面的一个分类定理。对于更高维的四元数射影空间中极小曲面的研究就更为困难, 取得的结论也比较少。He和Jiao^[7]给出$ \mathbb{H}$Pⁿ中具有平行第二基本形式的共形极小二维球面的分类结果。

由于扭映射给出$ \mathbb{H}$Pⁿ与$ \mathbb{C}$P²ⁿ⁺¹水平部分的一个等同, 而复射影空间中极小曲面的研究有很多已知的结果, 因此扭映射是研究四元数射影空间的一个重要工具。本文正是利用映射π:$ \mathbb{C}$P⁷→$ \mathbb{H}$P³构造$ \mathbb{H}$P³中共形极小曲面的例子。

1 预备知识

用符号$ \mathbb{H}$表示所有四元数组成的集合, 那么$ \mathbb{H}$是一个以1, i, j, k为基的四维实向量空间, 并且$ \mathbb{H}$上有环运算如下：

$ \begin{array}{*{20}{c}} {{{\rm{i}}^2} = {{\rm{j}}^2} = {{\rm{k}}^2} = - 1,{\rm{ij}} = {\rm{k}} = - {\rm{ji,}}}\\ {{\rm{jk}} = {\rm{i}} = - {\rm{kj}},{\rm{ki}} = {\rm{j}} = - {\rm{ik}}{\rm{.}}} \end{array} $

通常, 把$ \mathbb{H}$看成是复数域$ \mathbb{C}$上的一个以1, j为基的二维右模。对于任意的z=z₁+jz₂, w=w₁+jw₂∈$ \mathbb{H}$, 有

$ \mathit{\boldsymbol{zw}} = \left( {{\mathit{\boldsymbol{z}}_1}{\mathit{\boldsymbol{w}}_1} - {{\mathit{\boldsymbol{\bar z}}}_2}{\mathit{\boldsymbol{w}}_2}} \right) + {\rm{j}}\left( {{\mathit{\boldsymbol{z}}_2}{\mathit{\boldsymbol{w}}_1} + {{\mathit{\boldsymbol{\bar z}}}_1}{\mathit{\boldsymbol{w}}_2}} \right), $

可以验证该乘法与上述环运算是等价的。

在四元数$ \mathbb{H}$上有一个自然的共轭运算：

$ {\left( {{\mathit{\boldsymbol{z}}_1} + {\rm{j}}{\mathit{\boldsymbol{z}}_2}} \right)^ * } = {{\mathit{\boldsymbol{\bar z}}}_1} - {\rm{j}}{\mathit{\boldsymbol{z}}_2}. $

用$ \mathbb{H}$ⁿ表示四元数n元组构成的集合, 本文把$ \mathbb{H}$ⁿ中的元素写成列向量的形式。那么$ \mathbb{H}$ⁿ与$ \mathbb{C}$²ⁿ有一个自然的等同：

$ {\mathit{\boldsymbol{z}}_1} + {\rm{j}}{\mathit{\boldsymbol{z}}_2} \mapsto \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_1}}\\ {{\mathit{\boldsymbol{z}}_2}} \end{array}} \right). $

四元数射影空间$ \mathbb{H}$Pⁿ表示$ \mathbb{H}$ⁿ⁺¹中的四元数直线组成的集合, 即对于[v₁]$ _\mathbb{H}$和[v₂]$ _\mathbb{H}$∈$ \mathbb{H}$Pⁿ, [v₁]$ _\mathbb{H}$=[v₂]$ _\mathbb{H}$当且仅当∃x∈$ \mathbb{H}$, 使得v₂=v₁x.

辛群Sp(n)={A∈GL(n; $ \mathbb{H}$)|A^*T·A=I_n}, 其中I_n表示n阶单位矩阵。对于A∈Sp(n+1), [v]$ _\mathbb{H}$∈$ \mathbb{H}$Pⁿ, n+1阶辛群Sp(n+1)在$ \mathbb{H}$Pⁿ上有一个自然的作用：

$ \mathit{\boldsymbol{A}} \cdot {\left[ \mathit{\boldsymbol{v}} \right]_\mathbb{H}} = {\left[ {\mathit{\boldsymbol{Av}}} \right]_\mathbb{H}}, $

可以验证该作用是可迁的, 并且G₀=Sp(1)×Sp(n)是该作用在[(1, 0, …, 0)^T]$ _\mathbb{H}$∈$ \mathbb{H}$Pⁿ处的迷向群。因此, $ \mathbb{H}$Pⁿ的齐性表示为

$ \mathbb{H}{P^n} = Sp\left( {n + 1} \right)/Sp\left( 1 \right) \times Sp\left( n \right). $

辛群Sp(n+1)可以看做是特殊酉群SU(2n+2)中的一个子群：Sp(n+1)$ \hookrightarrow $SU(2n+2), X+jY$ \mapsto \left( \begin{array}{l} \mathit{\boldsymbol{X}}\;\;\;{\rm{ - }}\mathit{\boldsymbol{\bar Y}}\\ \mathit{\boldsymbol{Y}}\;\;\;\;\;\mathit{\boldsymbol{\bar X}} \end{array} \right)$, 其中X, Y∈GL(n+1;$ \mathbb{C}$).这样可以得到下面的一个交换图：

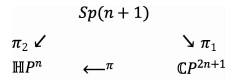
其中π:$ \mathbb{C}$P²ⁿ⁺¹→$ \mathbb{H}$Pⁿ, $ \left[ \begin{array}{l} {\mathit{\boldsymbol{z}}_{\rm{1}}}\\ {\mathit{\boldsymbol{z}}_2} \end{array} \right] \mapsto $[z₁+jz₂]$ _\mathbb{H}$, z₁, z₂∈$ \mathbb{C}$ⁿ⁺¹, 是扭映射, 它是一个纤维化。

如果A=X+jY∈Sp(n+1), 记A=(A₀, …, A_n), X=(X₀, …, X_n), Y=(Y₀, …, Y_n), 那么π₁(A)= $ \left[ \begin{array}{l} {\mathit{X}_{\rm{0}}}\\ {\mathit{Y}_{\rm{0}}} \end{array} \right]$和π₂(A)=[A₀]$ _\mathbb{H}$为自然投影。要说明上述图为交换图, 需要保证π₁是一个满射。而Sp(n+1)→$ \mathbb{C}$P²ⁿ⁺¹是一个以U(1)×Sp(n)为结构群的主纤维丛, 因此π₁自然是一个满射。所以, 上述图表可交换。

定义1.1  由于扭映射是一个纤维化, 因此$ \mathbb{C}$P²ⁿ⁺¹上的水平分布$ \mathscr{H}$定义为纤维切空间的正交补部分, 其中$ \mathbb{C}$P²ⁿ⁺¹上的度量为Fubini-Study度量。特别的, 当M是一个黎曼面的时候, 如果f:M→$ \mathbb{C}$P²ⁿ⁺¹的切映射的像在$ \mathscr{H}$中, 则称f为水平曲面。

根据文献[1], 对于[z]∈$ \mathbb{C}$P²ⁿ⁺¹, 记z=$ \left( \begin{array}{l} {\mathit{\boldsymbol{z}}_{\rm{1}}}\\ {\mathit{\boldsymbol{z}}_2} \end{array} \right)$, 那么有下述等同：

$ \begin{array}{*{20}{c}} {{\mathscr{H}_{\left[ z \right]}} \leftrightarrow \left\{ {\mathit{\boldsymbol{w}} \in {\mathit{\boldsymbol{z}}^ \bot }\left| {{\sigma _z}\left( \mathit{\boldsymbol{w}} \right) = 0} \right.,{\sigma _z} = } \right.}\\ {\left. { - \mathit{\boldsymbol{z}}_2^{\rm{T}}{\rm{d}}{\mathit{\boldsymbol{z}}_1} + \mathit{\boldsymbol{z}}_1^{\rm{T}}{\rm{d}}{\mathit{\boldsymbol{z}}_2}} \right\},} \end{array} $

(1)

其中z₁, z₂∈$ \mathbb{C}$ⁿ⁺¹.

2 $ \mathbb{H}$P³中的共形极小曲面

在本节中, 利用扭映射π:$ \mathbb{C}$P⁷→$ \mathbb{H}$P³来构造$ \mathbb{H}$P³中的共形极小曲面.

2.1 $ \mathbb{C}$P²ⁿ⁺¹中曲面水平的等价条件

在本小节中, 将介绍$ \mathbb{H}$Pⁿ的上度量, 并从度量的角度给出$ \mathbb{C}$P²ⁿ⁺¹中曲面水平的一个等价条件。

用Ω表示Sp(n+1)上的Maurer-Cartan形式, 即Ω是Sp(n+1)上的一个取值在$ \mathscr{sp}$(n+1)上的左不变1-形式, Ω=(Ω_β^α), 0≤α, β≤n.

由$ \mathbb{H}$Pⁿ的齐性表示$ \mathbb{H}$Pⁿ=Sp(n+1)/Sp(1)×Sp(n), 可以得到李代数的分解：

$ \mathscr{g} = {\mathscr{g}_0} \oplus \mathscr{m}, $

其中$ \mathscr{g}$为Sp(n+1)的李代数, $ \mathscr{g}_0$为G₀的李代数, $ \mathscr{m}{\rm{ = }}\left\{ {\left( \begin{array}{l} 0\;\;\; - {\mathit{\boldsymbol{X}}^{*{\rm{T}}}}\\ \mathit{\boldsymbol{X}}\;\;\;\;\;\;{\rm{0}} \end{array} \right):\mathit{\boldsymbol{X}} \in \mathbb{H}{^\mathit{n}}} \right\}$.

因此,

$ \sum\limits_{a = 1}^n {\mathit{\Omega }_0^{\alpha * } \cdot \mathit{\Omega }_0^\alpha } $

是$ \mathscr{m}$上的一个不变的内积, 那么根据齐性空间中不变度量的结论^[8], 它给出了$ \mathbb{H}$Pⁿ上的一个不变度量：

$ {\text{d}}s_{\mathbb{H}{P^n}}^2 = \sum\limits_{a = 1}^n {\omega _0^{\alpha * } \cdot \omega _0^\alpha } , $

(2)

其中ω=s^*Ω, s:U⊂$ \mathbb{H}$Pⁿ→Sp(n+1)为任意一个局部截面。在该不变度量下, 辛群Sp(n+1)是$ \mathbb{H}$Pⁿ的等距群。

在预备知识中, 我们知道Sp(n+1)$ \hookrightarrow$SU(2n+2), X+jY$ \mapsto \left( \begin{array}{l} \mathit{\boldsymbol{X}}\;\;\;{\rm{ - }}\mathit{\boldsymbol{\bar Y}}\\ \mathit{\boldsymbol{Y}}\;\;\;\;\;\mathit{\boldsymbol{\bar X}} \end{array} \right)$, 在该等同下, $ \mathbb{C}$P²ⁿ⁺¹有齐性表示：$ \mathbb{C}$P²ⁿ⁺¹=Sp(n+1)/U(1)×Sp(n).

类似于$ \mathbb{H}$Pⁿ的情况, 令$ \mathit{\tilde \Omega }{\rm{ = }}\left( {\mathit{\tilde \Omega }_\mathit{B}^\mathit{A}} \right)$, 0≤A, B≤2n+1, 为Sp(n+1)$ \hookrightarrow$SU(2n+2)上的Maurer-Cartan形式。取$ {\mathit{\tilde s}}$:U⊂$ \mathbb{C}$P²ⁿ⁺¹→Sp(n+1)为任意一个局部截面, 记$ \mathit{\tilde \omega }{\rm{ = }}{\mathit{s}^*}\mathit{\tilde \Omega }$, 则$ \mathbb{C}$P²ⁿ⁺¹上的不变度量为：

$ {\text{d}}s_{\mathbb{C}{P^{2n + 1}}}^2 = \sum\limits_{A = 1}^{2n + 1} {\bar {\tilde \omega} _0^A \cdot \tilde \omega _0^A} . $

(3)

取g=X+jY∈Sp(n+1), 则

$ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = {\mathit{\boldsymbol{g}}^{ - 1}}{\rm{d}}\mathit{\boldsymbol{g}}, $

(4)

$ \mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }}= {\left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{X}}&{ - \mathit{\boldsymbol{\bar Y}}}\\ \mathit{\boldsymbol{Y}}&{ \mathit{\boldsymbol{\bar X}}} \end{array}} \right)^{ - 1}}{\rm{d}}\left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{X}}&{ - \mathit{\boldsymbol{\bar Y}}}\\ \mathit{\boldsymbol{Y}}&{ \mathit{\boldsymbol{\bar X}}} \end{array}} \right). $

(5)

为方便起见, 引入记号Ω_β^α=Γ_β^α+jΣ_β^α, 其中Γ_β^α和Σ_β^α为复值1-形式。

则式(4)和式(5)可以写成(为书写方便, 本文仅给出n=3的情形, 一般的情况只是矩阵的维数不同, 并没有本质区别)：

$ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \left( {\begin{array}{*{20}{c}} {\mathit{\Omega }_0^0}&{\mathit{\Omega }_1^0}&{\mathit{\Omega }_2^0}&{\mathit{\Omega }_3^0}\\ {\mathit{\Omega }_0^1}&{\mathit{\Omega }_1^1}&{\mathit{\Omega }_2^1}&{\mathit{\Omega }_3^1}\\ {\mathit{\Omega }_0^2}&{\mathit{\Omega }_1^2}&{\mathit{\Omega }_2^2}&{\mathit{\Omega }_3^2}\\ {\mathit{\Omega }_0^3}&{\mathit{\Omega }_1^3}&{\mathit{\Omega }_2^3}&{\mathit{\Omega }_3^3} \end{array}} \right), $

(6)

$ \mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }} = \left( {\begin{array}{*{20}{c}} {\mathit{\Gamma }_0^0}&{\mathit{\Gamma }_1^0}&{\mathit{\Gamma }_2^0}&{\mathit{\Gamma }_3^0}&{ - \mathit{\Sigma }_0^0}&{ - \mathit{\Sigma }_1^0}&{ - \mathit{\Sigma }_2^0}&{ - \mathit{\Sigma }_3^0}\\ {\mathit{\Gamma }_0^1}&{\mathit{\Gamma }_1^1}&{\mathit{\Gamma }_2^1}&{\mathit{\Gamma }_3^1}&{ - \mathit{\Sigma }_0^1}&{ - \mathit{\Sigma }_1^1}&{ - \mathit{\Sigma }_2^1}&{ - \mathit{\Sigma }_3^1}\\ {\mathit{\Gamma }_0^2}&{\mathit{\Gamma }_1^2}&{\mathit{\Gamma }_2^2}&{\mathit{\Gamma }_3^2}&{ - \mathit{\Sigma }_0^2}&{ - \mathit{\Sigma }_1^2}&{ - \mathit{\Sigma }_2^2}&{ - \mathit{\Sigma }_3^2}\\ {\mathit{\Gamma }_0^3}&{\mathit{\Gamma }_1^3}&{\mathit{\Gamma }_2^3}&{\mathit{\Gamma }_3^3}&{ - \mathit{\Sigma }_0^3}&{ - \mathit{\Sigma }_1^3}&{ - \mathit{\Sigma }_2^3}&{ - \mathit{\Sigma }_3^3}\\ {\mathit{\Sigma }_0^0}&{\mathit{\Sigma }_1^0}&{\mathit{\Sigma }_2^0}&{\mathit{\Sigma }_3^0}&{\mathit{\Gamma }_0^0}&{\mathit{\Gamma }_1^0}&{\mathit{\Gamma }_2^0}&{\mathit{\Gamma }_3^0}\\ {\mathit{\Sigma }_0^1}&{\mathit{\Sigma }_1^1}&{\mathit{\Sigma }_2^1}&{\mathit{\Sigma }_3^1}&{\mathit{\Gamma }_0^1}&{\mathit{\Gamma }_1^1}&{\mathit{\Gamma }_2^1}&{\mathit{\Gamma }_3^1}\\ {\mathit{\Sigma }_0^2}&{\mathit{\Sigma }_1^2}&{\mathit{\Sigma }_2^2}&{\mathit{\Sigma }_3^2}&{\mathit{\Gamma }_0^2}&{\mathit{\Gamma }_1^2}&{\mathit{\Gamma }_2^2}&{\mathit{\Gamma }_3^2}\\ {\mathit{\Sigma }_0^3}&{\mathit{\Sigma }_1^3}&{\mathit{\Sigma }_2^3}&{\mathit{\Sigma }_3^3}&{\mathit{\Gamma }_0^3}&{\mathit{\Gamma }_1^3}&{\mathit{\Gamma }_2^3}&{\mathit{\Gamma }_3^3} \end{array}} \right), $

(7)

下面的定理是$ \mathbb{C}$P²ⁿ⁺¹曲面水平的一个等价条件。

定理2.1  设Φ:M→$ \mathbb{C}$P²ⁿ⁺¹是一个浸入, 则Φ水平当且仅当e^*Σ₀⁰=0, 其中e:U⊂M→Sp(n+1)是沿Φ的活动标架。

证明  取e:U⊂M→Sp(n+1)是沿Φ的活动标架, 则π₁∘e=Φ, 其中π₁:Sp(n+1)→$ \mathbb{C}$P²ⁿ⁺¹为自然投影。根据预备知识中的交换图, 有π₂=π∘π₁, 所以

$ {\pi _2} \circ e = \pi \circ {\pi _1} \circ e = \pi \circ \mathit{\Phi }, $

即e:U⊂M→Sp(n+1)也是一个沿π∘Φ:M→$ \mathbb{H}$Pⁿ的活动标架。

由式(2), 式(3), 式(6)和式(7), 有

$ \begin{array}{*{20}{c}} {{{\left( {\pi \circ \mathit{\Phi }} \right)}^ * }{\text{d}}s_{\mathbb{H}{P^n}}^2 = \sum\limits_{a = 1}^n {\bar \gamma _0^a \cdot \gamma _0^a} + \sum\limits_{a = 1}^n {\bar \sigma _0^a \cdot \sigma _0^a} ,} \\ {{\mathit{\Phi }^ * }{\text{d}}s_{\mathbb{C}{P^{2n + 1}}}^2 = \sum\limits_{a = 1}^n {\bar \gamma _0^a \cdot \gamma _0^a} + \sum\limits_{a = 0}^n {\bar \sigma _0^a \cdot \sigma _0^a} } \\ { = {{\left( {\pi \circ \mathit{\Phi }} \right)}^ * }{\text{d}}s_{\mathbb{H}{P^n}}^2 + \bar \sigma _0^0 \cdot \sigma _0^0,} \end{array} $

其中γ=e^*Γ, σ=e^*Σ.

根据题设Φ水平, 则Φ*ds$ \mathbb{C}$P2n+12=(π∘Φ)*ds$ \mathbb{H}$Pn2.

所以, Φ水平当且仅当e^*Σ₀⁰=0.

定理2.1是从度量的角度来刻画曲面水平的条件的, 它与预备知识中的式(1)是从两个不同角度说明曲面水平, 它们是等价的.

2.2 $ \mathbb{C}$P⁷中的水平全纯曲面

接下来考虑Φ:M→$ \mathbb{C}$P⁷是一个水平极小浸入, 其中M是一个黎曼面。

设$ \mathbb{C}$P⁷中点的齐次坐标为[(z₁⁰, z₁¹, z₁², z₁³, z₂⁰, z₂¹, z₂², z₂³)^T], 令U_i表示$ \mathbb{C}$P⁷中第(i+1)个齐次坐标不为0的点集, i=0, 1, …, 7, 则{U_i}_i=0⁷是$ \mathbb{C}$P⁷的一个坐标覆盖。

由预备知识中的式(1), 我们知道Φ在M中任意一点水平当且仅当Φ^*σ=0, 其中σ=-z₂^Tdz₁+z₁^Tdz₂.

情形1： Φ(M)∩U₀≠∅.

在坐标卡U₀中, 令Φ=[(1, z₁¹, z₁², z₁³, z₂⁰, z₂¹, z₂², z₂³)^T],

$ \begin{array}{*{20}{c}} {{\mathit{\Phi }^ * }\sigma = - \left( {z_2^0,z_2^1,z_2^2,z_2^3} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} 1\\ {z_1^1}\\ {z_1^2}\\ {z_1^3} \end{array}} \right) + \left( {1,z_1^1,z_1^2,z_1^3} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} {z_2^0}\\ {z_2^1}\\ {z_2^2}\\ {z_2^3} \end{array}} \right) = }\\ {{\rm{d}}z_2^0 + z_1^1{\rm{d}}z_2^1 + z_1^2{\rm{d}}z_2^2 + z_1^3{\rm{d}}z_2^3 - z_2^1{\rm{d}}z_1^1 - z_2^2{\rm{d}}z_1^2 - }\\ {z_2^3{\rm{d}}z_1^3 = {\rm{d}}\left( {z_2^0 + z_1^1z_2^1 + z_1^2z_2^2 + z_1^3z_2^3} \right) - 2z_2^1{\rm{d}}z_1^1 - }\\ {2z_2^2{\rm{d}}z_1^2 - 2z_2^3{\rm{d}}z_1^3.} \end{array} $

情形1.1：z₁¹, z₁², z₁³均为常数

令z₁¹=a₁, z₁²=a₂, z₁³=a₃, 因为d(z₂⁰+a₁z₂¹+a₂z₂²+a₃z₂³)=0, 所以z₂⁰+a₁z₂¹+a₂z₂²+a₃z₂³=a₄(a₄为常数)。假设z₂¹=g₁, z₂²=g₂, z₂³=g₃, 则g₁, g₂, g₂为M上的亚纯函数(特别地, 可以为常数)因为Φ全纯。因此, 此时有

$ \begin{array}{*{20}{c}} {\mathit{\Phi } = \left[ {\left( {1,{a_1},{a_2},{a_3},{a_4} - {a_1}{g_1} - {a_2}{g_2} - } \right.} \right.}\\ {\left. {{{\left. {{a_3}{g_3},{g_1},{g_2},{g_3}} \right)}^{\rm{T}}}} \right].} \end{array} $

情形1.2：z₁¹, z₁², z₁³不全为常数

不失一般性, 假设z₁³不为常数, 否则通过一个置换矩阵作用Φ可转换为此情形, 因此在相差一个置换矩阵作用的意义下, 可以假设z₁³不为常数。

设z₂⁰+z₁¹z₂¹+z₁²z₂²+z₁³z₃²=g₀, z₁¹=g₁, z₁²=g₂, z₁³=g₃, z₂¹=g₄, z₂²=g₅, 则g_m为M上的亚纯函数, m=0, …, 5.由于d(z₂⁰+z₁¹z₂¹+z₁²z₂²+z₁³z₂³)=2z₂¹dz₁¹+2z₂²dz₁²+2z₂³dz₁³, 因此z₂³= $ \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}} - {\mathit{g}_{\rm{4}}}\frac{{{\rm{d}}{\mathit{g}_1}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}} - {\mathit{g}_{\rm{5}}}\frac{{{\rm{d}}{\mathit{g}_2}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}}$。所以, 此时有

$ \begin{array}{*{20}{c}} {\mathit{\Phi } = \left[ {\left( {1,{g_1},{g_2},{g_3},{g_0} - {g_1}{g_4} - {g_2}{g_5} - } \right.} \right.}\\ {{g_3}\left( {\frac{1}{2}\frac{{{\rm{d}}{g_0}}}{{{\rm{d}}{g_3}}} - {g_4}\frac{{{\rm{d}}{g_1}}}{{{\rm{d}}{g_3}}} - {g_5}\frac{{{\rm{d}}{g_2}}}{{{\rm{d}}{g_3}}}} \right),}\\ {\left. {{{\left. {{g_4},{g_5},\frac{1}{2}\frac{{{\rm{d}}{g_0}}}{{{\rm{d}}{g_3}}} - {g_4}\frac{{{\rm{d}}{g_1}}}{{{\rm{d}}{g_3}}} - {g_5}\frac{{{\rm{d}}{g_2}}}{{{\rm{d}}{g_3}}}} \right)}^{\rm{T}}}} \right],} \end{array} $

特别的, 此时g₁, g₂, g₄和g₅可以取常数.

情形2： Φ(M)∩U₀=∅, Φ(M)∩U₁≠∅

令Φ=[(0, 1, z₁², z₁³, z₂⁰, z₂¹, z₂², z₂³)^T],

$ \begin{array}{l} {\mathit{\Phi }^ * }\sigma = - \left( {z_2^0,z_2^1,z_2^2,z_2^3} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} 0\\ 1\\ {z_1^2}\\ {z_1^3} \end{array}} \right) + \left( {0,1,z_1^2,z_1^3} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} {z_2^0}\\ {z_2^1}\\ {z_2^2}\\ {z_2^3} \end{array}} \right)\\ = {\rm{d}}z_2^1 + z_1^2{\rm{d}}z_2^2 + z_1^3{\rm{d}}z_2^3 - z_2^2{\rm{d}}z_1^2 - z_2^3{\rm{d}}z_1^3 = \\ {\rm{d}}\left( {z_2^1 + z_1^2z_2^2 + z_1^3z_2^3} \right) - 2z_2^2{\rm{d}}z_1^2 - 2z_2^3{\rm{d}}z_1^3. \end{array} $

情形2.1：z₁², z₁³均为常数

令z₁²=a₁, z₁³=a₂, 因为d(z₂¹+a₁z₂²+a₂z₂³)=0, 所以z₂¹+a₁z₂²+a₂z₂³=a₃(a₃为常数)。令z₂⁰=g₁, z₂²=g₂, z₂³=g₃, 则g₁, g₂, g₂为M上的亚纯函数(特别地, 可以为常数)。所以, 有

$ \mathit{\Phi }{\rm{ = }}\left[ {\left( {0,1,{\mathit{a}_{\rm{1}}},{\mathit{a}_{\rm{2}}},{\mathit{g}_{\rm{1}}},{\mathit{a}_{\rm{3}}} - {\mathit{a}_{\rm{1}}}{\mathit{g}_2} - {\mathit{a}_{\rm{2}}}{\mathit{g}_3},{\mathit{g}_2},{\mathit{g}_3}} \right)^{\rm{T}}} \right]. $

情形2.2：z₁², z₁³不全为常数

类似于情形1.2, 可以假设z₁³不为常数。

设z₂¹+z₁²z₂²+z₁³z₂³=g₀, z₁²=g₁, z₁³=g₂, z₂⁰=g₃, z₂²=g₄, 则g_m为M上的亚纯函数, m=0, …, 4.由于d(z₂¹+z₁²z₂²+z₁³z₂³)=2z₂²dz₁²+2z₂³dz₁³, 因此, z₂³=$ \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_{\rm{2}}}}} - {\mathit{g}_{\rm{4}}}\frac{{{\rm{d}}{\mathit{g}_1}}}{{{\rm{d}}{\mathit{g}_2}}}$。所以, 此时有

$ \begin{array}{*{20}{c}} {\mathit{\Phi } = \left[ {\left( {0,1,{g_1},{g_2},{g_3},{g_0} - {g_1}{g_4} - } \right.} \right.}\\ {\left. {{{\left. {{g_2}\left( {\frac{1}{2}\frac{{{\rm{d}}{g_0}}}{{{\rm{d}}{g_2}}} - {g_4}\frac{{{\rm{d}}{g_1}}}{{{\rm{d}}{g_2}}}} \right),{g_4},\frac{1}{2}\frac{{{\rm{d}}{g_0}}}{{{\rm{d}}{g_2}}} - {g_4}\frac{{{\rm{d}}{g_1}}}{{{\rm{d}}{g_2}}}} \right)}^{\rm{T}}}} \right],} \end{array} $

特别的, 此时g₁, g₃和g₄可以取常数.

情形3： Φ(M)∩(U₀∪U₁)=∅, Φ(M)∩U₂≠∅

令Φ=[(0, 0, 1, z₁³, z₂⁰, z₂¹, z₂², z₂³)^T],

$ \begin{array}{*{20}{c}} {{\mathit{\Phi }^ * }\sigma = - \left( {z_2^0,z_2^1,z_2^2,z_2^3} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} 0\\ 0\\ 1\\ {z_1^3} \end{array}} \right) + \left( {0,0,1,z_1^3} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} {z_2^0}\\ {z_2^1}\\ {z_2^2}\\ {z_2^3} \end{array}} \right)}\\ { = {\rm{d}}z_2^2 + z_1^3{\rm{d}}z_2^3 - z_2^3{\rm{d}}z_1^3}\\ { = {\rm{d}}\left( {z_2^2 + z_1^3z_2^3} \right) - 2z_2^3{\rm{d}}z_1^3.} \end{array} $

情形3.1：z₁³为常数

令z₁³=a₁, 因为d(z₂²+a₁z₂³)=0, 所以z₂²+a₁z₂³=a₂(a₂为常数)。令z₂⁰=g₁, z₂¹=g₂, z₂³=g₃, 则g₁, g₂, g₃为M上的亚纯函数(特别地, 可以取常数)。所以, 有

$ \mathit{\Phi } = \left[ {{{\left( {0,0,1,{a_1},{g_1},{g_2},{a_2} - {a_1}{g_3},{g_3}} \right)}^{\rm{T}}}} \right]. $

情形3.2：z₁³不为常数

设z₂²+z₁³z₂³=g₀, z₁³=g₁, z₂⁰=g₂, z₂²=g₃, 则g_m为M上的亚纯函数, m=0, …, 3.由于d(z₂²+z₁³z₂³)=2z₂³dz₁³, 因此, z₂³=$ \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_{\rm{1}}}}}$。所以, 此时有

$ \mathit{\Phi } = \left[ {{{\left( {0,0,1,{g_1},{g_2},{g_3},{g_0} - \frac{1}{2}{g_1}\frac{{{\rm{d}}{g_0}}}{{{\rm{d}}{g_1}}},\frac{1}{2}\frac{{{\rm{d}}{g_0}}}{{{\rm{d}}{g_1}}}} \right)}^{\rm{T}}}} \right], $

特别的, 此时g₁, g₃和g₄可以取常数.

情形4： Φ(M)∩(U₀∪U₁∪U₂)=∅, Φ(M)∩U₃≠∅

令Φ=[(0, 0, 0, 1, z₂⁰, z₂¹, z₂², z₂³)^T],

$ \begin{array}{*{20}{c}} {{\mathit{\Phi }^ * }\sigma = - \left( {z_2^0,z_2^1,z_2^2,z_2^3} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 1 \end{array}} \right) + \left( {0,0,0,1} \right){\rm{d}}\left( {\begin{array}{*{20}{c}} {z_2^0}\\ {z_2^1}\\ {z_2^2}\\ {z_2^3} \end{array}} \right)}\\ { = {\rm{d}}z_2^3.} \end{array} $

所以z₂³=a₁为常数, 设z₂⁰=g₁, z₂¹=g₂, z₂²=g₂, 则g₁, g₂和g₃为亚纯函数(可以取常数), 所以

$ \mathit{\Phi } = \left[ {{{\left( {0,0,0,1,{g_1},{g_2},{g_3},{a_1}} \right)}^{\rm{T}}}} \right]. $

情形5： Φ(M)∩(U₀∪U₁∪U₂∪U₃)=∅, Φ(M)∩U₄≠∅

令Φ=[(0, 0, 0, 0, 1, z₂¹, z₂², z₂³)^T], 此时Φ^*σ=0恒成立。

令z₂¹=g₁, z₂²=g₂, z₂³=g₃, 因此

$ \mathit{\Phi } = \left[ {{{\left( {0,0,0,0,1,{g_1},{g_2},{g_3}} \right)}^{\rm{T}}}} \right]. $

情形6： Φ(M)∩(U₀∪U₁∪U₂∪U₃∪U₄)=∅, Φ(M)∩U₅≠∅

令Φ=[(0, 0, 0, 0, 0, 1, z₂², z₂³)^T], 则Φ^*σ=0恒成立。设z₂²=g₁, z₂³=g₂, 因此

$ \mathit{\Phi } = \left[ {{{\left( {0,0,0,0,0,1,{g_1},{g_2}} \right)}^{\rm{T}}}} \right]. $

情形7： Φ(M)∩(U₀∪U₁∪U₂∪U₃∪U₄∪U₅)=∅, Φ(M)∩U₆≠∅

令Φ=[(0, 0, 0, 0, 0, 0, 1, z₂³)^T], 则Φ^*σ=0恒成立。设z₂³=g₁, 因此

$ \mathit{\Phi } = \left[ {{{\left( {0,0,0,0,0,0,1,{g_1}} \right)}^{\rm{T}}}} \right]. $

情形8： Φ(M)∩(U₀∪U₁∪U₂∪U₃∪U₄∪U₅∪U₆)=∅, Φ(M)∩U₇≠∅

此时Φ=[(0, 0, 0, 0, 0, 0, 0, 1)^T]退化, 这与Φ是浸入矛盾。

综合上述8个情形, 可以得到$ \mathbb{C}$P⁷中水平全纯曲面在局部上的一个分类定理。

定理2.2  假设Φ:M→$ \mathbb{C}$P⁷为水平全纯曲面, 则在相差一个置换矩阵作用的意义下, 局部上Φ一定可以写成下列形式之一：

1) Φ=[(1, a₁, a₂, a₃, a₄-a₁g₁-a₂g₂-a₃g₃, g₁, g₂, g₃)^T];

2) Φ=[(1, g₁, g₂, g₃, g₀-g₁g₄-g₂g₅-g₃($ \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}} - {\mathit{g}_{\rm{4}}}\frac{{{\rm{d}}{\mathit{g}_1}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}} - {\mathit{g}_{\rm{5}}}\frac{{{\rm{d}}{\mathit{g}_2}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}}$), g₄, g₅, $ \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}} - {\mathit{g}_{\rm{4}}}\frac{{{\rm{d}}{\mathit{g}_1}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}} - {\mathit{g}_{\rm{5}}}\frac{{{\rm{d}}{\mathit{g}_2}}}{{{\rm{d}}{\mathit{g}_{\rm{3}}}}}$)^T];

3) Φ=[(0, 1, a₁, a₂, g₁, a₃-a₁g₂-a₂g₃, g₂, g₃)^T];

4) Φ=[(0, 1, g₁, g₂, g₃, g₀-g₁g₄-g₂($ \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_{\rm{2}}}}} - {\mathit{g}_{\rm{4}}}\frac{{{\rm{d}}{\mathit{g}_1}}}{{{\rm{d}}{\mathit{g}_{\rm{2}}}}}$), g₄, $ \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_{\rm{2}}}}} - {\mathit{g}_{\rm{4}}}\frac{{{\rm{d}}{\mathit{g}_1}}}{{{\rm{d}}{\mathit{g}_{\rm{2}}}}}$)^T];

5) Φ=[(0, 0, 1, a₁, g₁, g₂, a₂-a₁g₃, g₃)^T];

6) Φ=[(0, 0, 1, g₁, g₂, g₃, g₀ $ {\rm{ - }}\frac{1}{2}{\mathit{g}_1}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_1}}} - \frac{1}{2}\frac{{{\rm{d}}{\mathit{g}_0}}}{{{\rm{d}}{\mathit{g}_1}}}$)^T];

7) Φ=[(0, 0, 0, 1, g₁, g₂, g₃, a₁)^T];

8) Φ=[(0, 0, 0, 0, 1, g₁, g₂, g₃)^T];

9) Φ=[(0, 0, 0, 0, 0, 1, g₁, g₂)^T];

10)Φ=[(0, 0, 0, 0, 0, 0, 1, g₁)^T].

其中g_m为M上的亚纯函数, a_n为常数, 其中m=0, …, 5, n=1, …, 4.

通过简单的直接计算可以验证定理2.2中所给出的10族共形极小曲面满足定理2.1中的条件。所以, 对于$ \mathbb{C}$P⁷中水平全纯曲面的构造可以采用定理2.1和式(1)中两种方式, 二者是等价的。

定理2.2给出$ \mathbb{C}$P⁷中水平全纯曲面的一个分类结果，接下来将利用该定理构造$ \mathbb{H}$P³中的共形极小曲面。

2.3 $ \mathbb{H}$P³中的共形极小曲面

首先，介绍Eells和Wood的一个结论^[9]。

引理2.1  设M，Y，N为黎曼流形，π：Y→N为黎曼淹没，f:M→Y是关于映射π的一个水平浸入，如果f调和，则π∘f:M→N也调和。

由于对于共形映射来说, 映射调和等价于映射极小^[5], 而$ \mathbb{C}$P⁷中的全纯曲面是$ \mathbb{C}$P⁷中的Kaehler子流形, Kaehler子流形一定是极小的, 因此, 有

命题2.1  设Φ:M→$ \mathbb{C}$P²ⁿ⁺¹是一个水平全纯曲面, 则π∘Φ:M→$ \mathbb{H}$Pⁿ是共形极小的, 其中π:$ \mathbb{C}$P²ⁿ⁺¹→$ \mathbb{H}$Pⁿ为扭映射。

由命题2.1可知, 定理2.2中给出的$ \mathbb{C}$P⁷中的10族水平全纯曲面在扭映射下的像就是$ \mathbb{H}$P³中的共形极小曲面。

例1  设g_m为黎曼面M上的亚纯函数, a_n为常数, m=0, …, 5, n=1, …, 4, 那么有$ \mathbb{H}$P³中的10族共形极小曲面如下：

1) $ \ {{\left[ \left( \begin{align} &\text{1} \\ &{{\mathit{a}}_{\text{1}}} \\ &{{\mathit{a}}_{\text{2}}} \\ &{{\mathit{a}}_{\text{3}}} \\ \end{align} \right)\text{+j}\left( \begin{matrix} {{\mathit{a}}_{\text{4}}}\text{-}{{\mathit{a}}_{\text{1}}}{{\mathit{g}}_{\text{1}}}\text{-}{{\mathit{a}}_{\text{2}}}{{\mathit{g}}_{\text{2}}}\text{-}{{\mathit{a}}_{\text{3}}}{{\mathit{g}}_{\text{3}}} \\ {{\mathit{g}}_{\text{1}}} \\ {{\mathit{g}}_{\text{2}}} \\ {{\mathit{g}}_{\text{3}}} \\ \end{matrix} \right) \right]}_{\mathbb{H}}}\text{:}\mathit{M}\to \mathbb{H}{{\mathit{P}}^{\text{3}}}\text{;}$

2) $ {{\left[ \left( \begin{align} &\text{1} \\ &{{\mathit{g}}_{\text{1}}} \\ &{{\mathit{g}}_{\text{2}}} \\ &{{\mathit{g}}_{\text{3}}} \\ \end{align} \right)\text{+j}\left( \begin{matrix} {{\mathit{g}}_{\text{0}}}\text{-}{{\mathit{g}}_{\text{1}}}{{\mathit{g}}_{\text{4}}}\text{-}{{\mathit{g}}_{\text{2}}}{{\mathit{g}}_{\text{5}}}\text{-}{{\mathit{g}}_{\text{3}}}\text{(}\frac{1}{2}\frac{\text{d}{{\mathit{g}}_{\text{0}}}}{\text{d}{{\mathit{g}}_{\text{3}}}}\text{-} \\ {{\mathit{g}}_{\text{4}}}\frac{\text{d}{{\mathit{g}}_{\text{1}}}}{\text{d}{{\mathit{g}}_{\text{3}}}}\text{-}{{\mathit{g}}_{\text{5}}}\frac{\text{d}{{\mathit{g}}_{\text{2}}}}{\text{d}{{\mathit{g}}_{\text{3}}}}\text{)} \\ {{\mathit{g}}_{\text{4}}} \\ {{\mathit{g}}_{\text{5}}} \\ \frac{1}{2}\frac{\text{d}{{\mathit{g}}_{\text{0}}}}{\text{d}{{\mathit{g}}_{\text{3}}}}\text{-}{{\mathit{g}}_{\text{4}}}\frac{\text{d}{{\mathit{g}}_{\text{1}}}}{\text{d}{{\mathit{g}}_{\text{3}}}}\text{-}{{\mathit{g}}_{\text{5}}}\frac{\text{d}{{\mathit{g}}_{\text{2}}}}{\text{d}{{\mathit{g}}_{\text{3}}}} \\ \end{matrix} \right) \right]}_{\mathbb{H}}}\text{:}\mathit{M}\to \mathbb{H}{{\mathit{P}}^{\text{3}}}\text{;}$

3) $ {{\left[ \left( \begin{align} &\text{0} \\ &\text{1} \\ &{{\mathit{a}}_{\text{1}}} \\ &{{\mathit{a}}_{\text{2}}} \\ \end{align} \right)\text{+j}\left( \begin{matrix} {{\mathit{g}}_{\text{1}}} \\ {{\mathit{a}}_{\text{3}}}\text{-}{{\mathit{a}}_{\text{1}}}{{\mathit{g}}_{\text{2}}}\text{-}{{\mathit{a}}_{\text{2}}}{{\mathit{g}}_{\text{3}}} \\ {{\mathit{g}}_{\text{2}}} \\ {{\mathit{g}}_{\text{3}}} \\ \end{matrix} \right) \right]}_{\mathbb{H}}}\text{:}\mathit{M}\to \mathbb{H}{{\mathit{P}}^{\text{3}}}\text{;}$

4) $ {{\left[ \left( \begin{align} &0 \\ &1 \\ &{{g}_{1}} \\ &{{g}_{2}} \\ \end{align} \right)+\text{j}\left( \begin{matrix} {{g}_{3}} \\ {{g}_{0}}-{{g}_{1}}{{g}_{4}}-{{g}_{2}}(\frac{1}{2}\frac{\text{d}{{g}_{0}}}{\text{d}{{g}_{2}}}-{{g}_{4}}\frac{\text{d}{{g}_{1}}}{\text{d}{{g}_{2}}}) \\ {{g}_{4}} \\ \frac{1}{2}\frac{\text{d}{{g}_{0}}}{\text{d}{{g}_{2}}}-{{g}_{4}}\frac{\text{d}{{g}_{1}}}{\text{d}{{g}_{2}}} \\ \end{matrix} \right) \right]}_{\mathbb{H}}}:M\to \mathbb{H}{{P}^{3}};$

5) $ {{\left[ \left( \begin{align} &0 \\ &0 \\ &1 \\ &{{a}_{1}} \\ \end{align} \right)+\text{j}\left( \begin{matrix} {{g}_{1}} \\ {{g}_{2}} \\ {{a}_{2}}-{{a}_{1}}{{g}_{3}} \\ {{g}_{3}} \\ \end{matrix} \right) \right]}_{\mathbb{H}}}:M\to \mathbb{H}{{P}^{3}};$

6) $ {{\left[ \left( \begin{align} &0 \\ &0 \\ &1 \\ &{{g}_{1}} \\ \end{align} \right)+\text{j}\left( \begin{matrix} {{g}_{2}} \\ {{g}_{3}} \\ {{g}_{0}}-\frac{1}{2}{{g}_{1}}\frac{\text{d}{{g}_{0}}}{\text{d}{{g}_{1}}} \\ \frac{1}{2}\frac{\text{d}{{g}_{0}}}{\text{d}{{g}_{1}}} \\ \end{matrix} \right) \right]}_{\mathbb{H}}}:M\to \mathbb{H}{{P}^{3}};$

7) ${{\left[ \left( \begin{matrix} 0 \\ 0 \\ 0 \\ 1 \\ \end{matrix} \right)\rm{+j}\left( \begin{matrix} {{\mathit{g}}_{\rm{1}}} \\ {{\mathit{g}}_{\rm{2}}} \\ {{\mathit{g}}_{\rm{3}}} \\ {{\mathit{a}}_{\rm{1}}} \\ \end{matrix} \right) \right]}_{\mathbb{H}}}:\mathit{M}\to \mathbb{H}{{\mathit{P}}^{\rm{3}}}\rm{;}$

8) $ {{\left[ \text{j}\left( \begin{align} &1 \\ &{{g}_{1}} \\ &{{g}_{2}} \\ &{{g}_{3}} \\ \end{align} \right) \right]}_{\mathbb{H}}}:M\to \mathbb{H}{{P}^{3}};$

9) $ {{\left[ \text{j}\left( \begin{align} &0 \\ &1 \\ &{{g}_{1}} \\ &{{g}_{2}} \\ \end{align} \right) \right]}_{\mathbb{H}}}:M\to \mathbb{H}{{P}^{3}};$

10) $ {{\left[ \text{j}\left( \begin{align} &0 \\ &0 \\ &1 \\ &{{g}_{1}} \\ \end{align} \right) \right]}_{\mathbb{H}}}:M\to \mathbb{H}{{P}^{3}}.$

在上述例子中, 可以选取不同形式的亚纯函数及常数, 因此上面的10个例子非常丰富。而$ \mathbb{H}$P³中极小曲面的分类依旧是一个很具有挑战性的研究课题, 需要解决的问题还很多。