2. 中国科学院空间信息处理与应用系统技术重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Geo-spatial Information Processing and Application System Technology, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
在图像的采集过程中,由于外部环境的影响,采集的图像不能有效地反映场景细节和对比度。因此,利用图像增强技术改善图像的视觉效果,增强图像细节和对比度,增加人眼可分辨的信息量,是十分必要的。特别是在数字摄影、视频通信、视频监测等领域中,高效率的图像增强算法得到了更为广泛的应用。
传统的图像增强算法按作用域可分为变换域和空间域两大类。变换域算法将图像转换到另一个域中,分别对不同分量进行处理,达到全局和局部的增强效果。这些算法计算复杂,耗时较长,还需要设置合适的相关参数。例如,Land[1]基于对人眼颜色恒常性的研究提出Retinex理论,后来,以此为基础,McCann[2],Jobson等[3-5]相继提出迭代式的多尺度Retinex,中心环绕式的单尺度Retinex(SSR)、多尺度Retinex(MSR)和多尺度Retinex彩色恢复(MSRCR)算法。Retinex算法在增强图像对比度的同时保持了颜色的恒常性,但在边界区域易产生光晕。文献[6-7]中基于小波变换的图像增强算法通过修改变换域的小波系数,在适当参数的选择下实现图像全局和局部的对比度增强。
虽然上述的变换域增强算法在很多领域中取得了较好的增强效果,但是同时也耗费了较长的运算时间,不适用于实时处理。因此,计算简单、效率高的空间域算法应用更为广泛。空间域增强算法可以分为全局和局部两大类。全局算法导出一种映射规则,将原始图像映射到增强图像上,从而扩展图像灰度级的动态范围。全局直方图均衡(HE)算法是最经典和应用最广泛的的全局算法之一,它能有效地增强图像对比度,但是如果直方图存在较大的峰值,输出图像则无法保持输入图像的亮度,并会产生难以接受的人工痕迹,影响视觉效果。为克服上述缺点,文献[8]提出局部直方图均衡算法,该算法利用像素周围的领域信息自适应地均衡,增强图像局部对比度。局部方法只是考虑局部窗口大小的灰度分布而忽略图像的整体特点,减弱了图像的层次感[9],并且计算量较大,窗口大小的选择要求较高,因此限制了其应用范围。
由于全局直方图均衡算法计算简单、效率高,许多学者对该方法进行大量的改进,形成一系列的改进算法。为防止图像过度增强,Kim[10]提出双直方图亮度保持直方图均衡化算法(BBHE),该算法通过输入图像的灰度级均值将其直方图分为两部分,分别对子直方图进行均衡化处理。接着,Wang等[11]提出等面积二元子图像直方图均衡算法(DSIHE),该算法遵循BBHE算法的思想,不同的是它以输入图像中值即像素中间值作为分割阈值。为保持图像亮度均值,Chen和Ramli[12]提出最小均值亮度差双直方图均衡算法(MMBEBHE),它选择输出图像与输入图像亮度误差最小的分割点作为阈值,达到适当增强的效果。这些算法相较于全局直方图均衡算法取得了更好的效果,但是生成的直方图只含有像素灰度级的频率信息,忽略了像素间的关联信息。因此,很多情况下增强后的图像人工痕迹明显,图像层次感减弱,直方图结构被破坏。
针对一维直方图丢弃了图像大量信息的问题,一些新的算法通过扩展直方图的概念进一步地表示图像的特征。Ceilk[13]提出一种基于二维直方图的算法,该二维直方图表示图像中像素与其邻域像素各灰度级对的数量,并以此扩大出现频次高的灰度级对的差异,从而实现图像的增强。然而,该算法在处理直方图存在较大峰值的图像时出现过度增强,产生过度拉伸的伪影。Lee等[14]也利用二维直方图,按灰度级对的差值进行分层,根据每一层的分布情况,进行约束优化获得每层的差分向量,再将每层的差分向量聚合成一个统一的差分向量,形成新的映射规则,得到增强图像。该算法在实验中取得了较好的效果,图像的整体和局部都得到增强。但是在处理整体背景偏暗的图像时,增强效果偏亮,而且对一些彩色图像增强后,色彩视觉效果有些失真。针对这些问题,本文对该算法进行改进,改善图像增强后偏亮和色彩失真的缺陷。
1 算法原理文献[14]提出基于分层差异表示(LDR)的全局增强算法。该算法利用表示相邻像素差异的二维直方图,该直方图仅仅反映相邻像素灰度级的差值,与视觉感知差异并不一致。本文根据视觉特性提出二维视觉差异直方图,基于该直方图,利用LDR结构对图像进行初步增强,采用灰度级补偿防止图像过增强,保持原图像的特征和层次感。对于彩色图像,由于HSV色度空间更接近于人眼的视觉特性,所以采用HSV将图像的色彩与亮度分离,对亮度分量V进行处理,再还原为彩色图像,从而保持图像色彩,达到增强的效果。
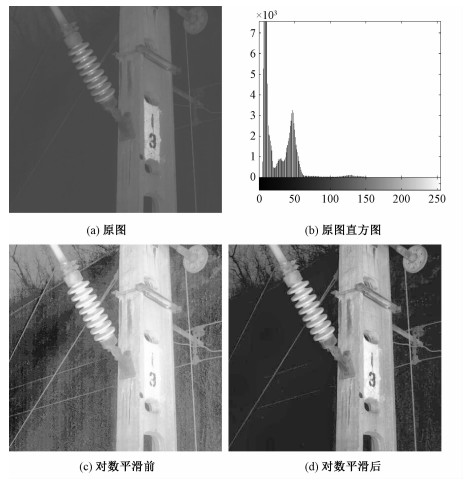
1.1 二维视觉差异直方图考虑一幅8位的灰度图像,其灰度级范围为0~255,即任一灰度级k∈[0, 255],其在图像增强后映射到灰度级xk。假设输入图像中2个相邻的像素灰度级分别为k和k+l,它们的差为l。定义二维直方图h(k, k+l),其表示输入图像中相邻2像素灰度级分别为k和k+l的出现的次数,本文采用8邻接的邻域。由于一些图像具有大量单一的背景或目标,其直方图灰度分布极不均匀,少数具有很大权重的灰度级对最终的映射函数产生绝对性的影响,使得映射函数产生极端变化,导致输出图像对比度过度拉伸而失真,采用对数函数对直方图进行平滑,使得灰度分布变得平缓,而且对数运算的非线性特性较为接近人眼视觉对亮度的感知能力。图 1给出对数平滑前后的结果对比。
|
Download:
|
| 图 1 对数平滑的结果对比 Fig. 1 Comparison of logarithmic smoothing results | |
从图 1(c)和1(d)结果对比看出,在处理灰度分布极不均匀的图像时,经过对数函数平滑后,对比度过度拉伸导致的失真现象得到明显改善。
在采用对数函数平滑后,排除相邻像素的先后顺序,可得一个无序的对数衰减的二维直方图,数学表达式如下:
| $ \begin{array}{*{20}{c}} {h_k^l = \log \left( {h\left( {k,k + l} \right) + h\left( {k + l,k} \right)} \right),}\\ {\left( {0 \le k \le 255 - l} \right).} \end{array} $ | (1) |
Weber定律表明人类恰可识别差异与物理量的初始值成正比, 即物理量初值越大, 可识别差异越大,其应用于人类对亮度的感知, 可得到如下结论:平均亮度越大处, 恰可感知的亮度差异越大[15]。因此,不同背景亮度下,相同的灰度级差异对人眼的刺激程度是不同的。为使二维直方图中的灰度差异与视觉差异一致,根据人眼的视觉特性,对二维直方图中每一个像素差值进行背景加权,权重值与该处背景灰度有关:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\upsilon }}_{i,j}} = {{\left( {\log \left( {av{g_{i,j}} + 2} \right)} \right)}^2},}\\ {av{g_{i,j}} = \frac{1}{2}\left( {\frac{1}{2}\left( {\frac{1}{4}\sum\limits_{{Q_1}} {f\left( {i,j} \right)} + \frac{1}{{4\sqrt 2 }}\sum\limits_{{Q_2}} {f\left( {i,j} \right)} } \right)} \right).} \end{array} $ | (2) |
式中:vi, j为图像在(i, j)处的权重;avgi, j为(i, j)处的背景灰度;f(i, j)表示(i, j)处的灰度级;Q1表示中心像素上下左右方向的4个相邻像素组成的集合;Q2表示中心像素对角线上的4个邻域像素组成的集合。
在得到图像各处的背景灰度权重后,就可利用该权重获得二维视觉差异直方图,计算公式如下:
| $ \begin{array}{*{20}{c}} {H_k^l = \log \left( {\sum\limits_{\forall i,j} {g_k^l\left( {i,j} \right)} } \right),}\\ {g_k^l\left( {i,j} \right) = {{\boldsymbol{\upsilon }} _{i,j}} \times \sum\limits_Q {P_k^l\left( {f\left( {i,j} \right),f\left( {i + a,j + b} \right)} \right)} ,}\\ { - 1 \le a,b \le 1}\\ {P_k^l\left( {s,t} \right) = \left\{ \begin{array}{l} 1,\;\;\;当\;s = k\;且\;\left| {s - t} \right| = l\\ 0,\;\;\;其他 \end{array} \right..} \end{array} $ | (3) |
式中:Hkl为背景加权后hkl;(i, j)为输入图像的任意一个像素位置;gkl(i, j)为图像(i, j)处相邻像素对灰度为k和k+l的数目加权值;f(i, j)为(i, j)处的灰度值;Q表示中心像素的8邻接的邻域;a、b都为整数;Pkl(s, t)为一个二进制功能函数,用来判断符合条件的相邻像素对。
由式(3)得到的二维直方图表示的相邻像素灰度差异与视觉差异基本一致,则利用该直方图,扩大出现相对频繁的差异,达到与视觉感知一致的增强效果。
1.2 分层差异表示在LDR算法[14]中,对输入图像中一对相邻像素,其灰度级为k和k+l,它们分别被映射到输出图像中的xk和xk+l灰度级。层l处的差变量dkl定义如下:
| $ d_k^l = {x_{k + l}} - {x_k},\left( {0 \le k \le 255 - l} \right). $ | (4) |
式中,输入图像中灰度级k和k+l的差l映射到输出图像灰度级xk和xk+l的差dkl。基于上述二维视觉差异直方图,当Hkl的值越大时,表明相邻像素灰度为k和k+l的状态出现越频繁,该差异信息越多,其灰度差值增强的必要性越大。因此使差分变量dkl与Hkl成正比例的变化以提高对比度是我们所期望的,对每一层l有如下所示关系:
| $ d_k^l = {K_l} \times H_k^l,\left( {0 \le k \le 255 - l} \right). $ | (5) |
式中:Kl是层l处的归一化比例常数。
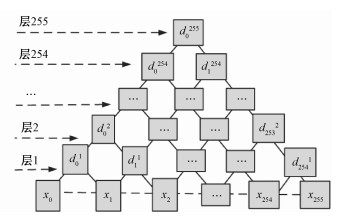
每层的差分变量dkl并不是独立的,其关系可用LDR结构表示,图 2给出LDR结构。在LDR中,输出图像灰度级xk可以由层1处的差变量dk1确定,关系如下:
| $ {x_k} = \sum\limits_{i = 0}^{k - 1} {d_i^1} ,\left( {1 \le k \le 255} \right). $ | (6) |
|
Download:
|
| 图 2 分层差异表示(LDR) Fig. 2 Layered difference representation (LDR) | |
为使动态范围最大化,令x0=0。
在LDR结构中,高层与低层有着紧密的联系,较高层l的差变量dkl也可由层1的差变量dk1来确定,将其包含的差变量dk1称为差变量dkl在层1的后代,表达式如下:
| $ d_k^l = \sum\limits_{i = k}^{k + l - 1} {d_i^1} ,\left( {0 \le k \le 255 - l} \right). $ | (7) |
式(7)推导过程如下:
| $ \begin{array}{l} d_k^l = {x_{k + l}} - {x_k}\\ \;\;\;\; = {x_{k + l}} - {x_{k + l - 1}} + {x_{k + l - 1}} - {x_{k + l - 2}} + \cdots + {x_{k + 1}} - {x_k}\\ \;\;\;\; = d_{k + l - 1}^1 + d_{k + l - 2}^1 + \cdots + d_k^1 = \sum\limits_{i = k}^{k + l - 1} {d_i^1} . \end{array} $ | (8) |
由此看出,差变量dkl可表示为多个层1的差变量dk1的和。
由输入图像的2D直方图Hkl,在满足式(5)和式(7)组成的系统前提下,获得层1处的差变量dk1。但是层1的差变量dk1比观测值Hkl要少,所以该系统是超定的。可以采用基于非负最小二乘(nonnegative least squares, NNLS)的非负约束算法来解决。然而差变量dkl具有强跨层关系,将所有层作为一个整体考虑,丢失了层与层之间的信息,易产生不规则伪影和噪声,因此有必要对每一层单独处理,再进行层间聚合。
对于任意一层l,由式(5)可知差变量dkl可由观测值Hkl得到,此外,式(7)表明每个dkl由多个dk1的和组成。由此,可将式(5)扩展为一个线性方程,表示如下:
| $ {\mathit{\boldsymbol{A}}_l}{\mathit{\boldsymbol{d}}_l} = {K_l}{\mathit{\boldsymbol{H}}_l}. $ | (9) |
式中:Al∈R(256-l)×255为由0和1组成的二元矩阵;dl=[d01, d11, …, d2541]T是层1的差向量;Hl=[H0l, H1l, …, H255-ll]T是2D直方图层为l的观测值向量。例如,层2的线性方程A2d2=K2H2如下所示:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 1&1&0& \cdots &0&0&0\\ 0&1&1& \cdots &0&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots \\ 0&0&0& \cdots &1&1&0\\ 0&0&0& \cdots &0&1&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {d_0^1}\\ {d_1^1}\\ \vdots \\ {d_{253}^1}\\ {d_{254}^1} \end{array}} \right] = }\\ {{K_2}\left[ {\begin{array}{*{20}{c}} {H_0^2}\\ {H_1^2}\\ \vdots \\ {H_{252}^2}\\ {H_{253}^2} \end{array}} \right].} \end{array} $ | (10) |
以此方式,在每一层l通过解约束优化问题获得差向量dl,约束优化系统如下:
| $ \left\{ \begin{array}{l} 优化问题:\min {\left\| {{\mathit{\boldsymbol{A}}_l}{\mathit{\boldsymbol{d}}_l} - {K_l}{\mathit{\boldsymbol{H}}_l}} \right\|^2}\\ 约束条件:{\mathit{\boldsymbol{d}}_l} \ge \mathit{\boldsymbol{0}},{\mathit{\boldsymbol{1}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_l} = 255 \end{array} \right.. $ | (11) |
式中:1和0分别表示其元素全为1和0的列向量。式(11)约束条件中前者表明差向量的所有元素都非负以保证变换函数X递增;后者将动态范围限定在0~255中。
为提高运算效率,减少式(11)的运算量,假设在层1中,差变量dk1具有相同的价值,给定差变量dkl,其在层1的后代满足
| $ d_i^1 = d_j^1,k \le i,j \le k + l - 1. $ | (12) |
这意味着灰度变换函数在xk和xk+l上线性递增,使得变换函数变得平滑,从而避免输出图像的伪影,因此这种均等是合理的。将式(12)应用到式(11)的约束优化系统中,采用最小二乘法进行求解。由于式(11)优化问题中二元矩阵Al为稀疏二元矩阵,矩阵元素只有0和1,可以将稀疏矩阵分解后再计算,获得最终的差向量dl计算公式,表达式如下:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{d}}_l} = \phi _l^{\max }\mathit{\boldsymbol{U}}_l^{ - 1}\left( {{\mathit{\boldsymbol{m}}_l} - \min \left( {{\mathit{\boldsymbol{m}}_l}} \right) \cdot \mathit{\boldsymbol{1}}} \right)\\ \phi _l^{\max } = \frac{{255}}{{{\mathit{\boldsymbol{1}}^{\rm{T}}}\mathit{\boldsymbol{U}}_l^{ - 1}{\mathit{\boldsymbol{m}}_l} - \min \left( {{\mathit{\boldsymbol{m}}_l}} \right) \cdot {\mathit{\boldsymbol{1}}^{\rm{T}}}\mathit{\boldsymbol{U}}_l^{ - 1}\mathit{\boldsymbol{1}}}} \end{array} \right.. $ | (13) |
式中,1表示其元素全为1的列向量。下面给出式(13)中Ul和ml的计算公式。
其中,Ul∈R255×255为对角矩阵,其第k个对角元素ukl由下式计算得到:
| $ \begin{array}{*{20}{c}} {u_k^l = \min \left( {k,256 - l} \right) - \max \left( {k - l,0} \right),}\\ {1 \le k \le 255.} \end{array} $ | (14) |
例如,在层l=5时,U5=diag[1, 2, 3, 4, 5, 5, …, 5, 5, 4, 3, 2, 1]。而ml可由式(9)中Hl获得,计算公式如下:
| $ {\mathit{\boldsymbol{m}}_l} = {\mathit{\boldsymbol{H}}_l}^ * {\mathit{\boldsymbol{1}}_l}. $ | (15) |
式中:1l为长度为l的单位列向量,所有元素均为1;符号*表示卷积运算。
由式(13)~式(15)可以得出每层的差分向量dl,其中1≤l≤255。现需合并这些单层差向量来形成统一的差向量d。
对于一般输入图像,当l越大,二维直方图Hl中大多数元素为零,表明其出现的频次很少,对图像的信息加强不大,并且在式(5)中我们期望dl的重要性与Hl成正相关。因此,将dl的重要性正比于
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{d}} = \frac{1}{{{\mathit{\boldsymbol{1}}^{\rm{T}}}\mathit{\boldsymbol{\omega }}}}\mathit{\boldsymbol{D}} \cdot \mathit{\boldsymbol{\omega }}\\ {\omega _l} = {\left( {\frac{{{s_l}}}{{{{\max }_i}{s_i}}}} \right)^\alpha },\mathit{\boldsymbol{D = }}\left[ {{\mathit{\boldsymbol{d}}_1},{\mathit{\boldsymbol{d}}_2}, \cdots ,{\mathit{\boldsymbol{d}}_l}, \cdots ,{\mathit{\boldsymbol{d}}_{255}}} \right] \end{array} \right.. $ | (16) |
式中:加权向量ω=[ω1, ω2, …, ω255]T,其第l个元素为ωl;D∈R255×255是一个矩阵,其第l列为差分向量dl;maxisi为所有sl中的最大值,此是归一化操作;α为幂律调整参数。当α较大时,有利于增强暗区细节;α较小时,有利于保留亮区细节。实验表明,当α>1.5效果较好。
由式(16)计算得到的统一差分矢量可用来获得灰度变换函数X,计算公式如下:
| $ \left\{ {\begin{array}{*{20}{c}} {{x_k} = \sum\limits_{i = 0}^{k - 1} {{d_i}} ,1 \le k \le 255}\\ {{x_0} = 0} \end{array}} \right.. $ | (17) |
根据式(17)得到变换函数X=[x0, x1, …, x255],然后可以重构输出图像。
1.3 灰度级补偿通过式(17)获得灰度变换函数后,以此重构图像,从而实现图像视觉增强的效果。然而,在对整体偏暗的图像进行增强时,出现一定程度的过增强,图像的亮区细节减少。这是由于输入图像大量的灰度级集中在较小的值,相邻像素的灰度差值较小,导致该部分产生过增强,在有限的灰度级动态范围内引起高层灰度级的合并,使得亮区细节减少,输出图像占用的灰度级减少,直方图结构遭到破坏。采用灰度级补偿的方法选择性地保留合并的灰度级,可以抑制暗区过增强的情况,保留更多的亮区细节。
考虑输入图像灰度级为[0, 1, …, k, …, 255],输出图像灰度级为[x0, x1, …, xk, …, x255],其中输入图像占用m个灰度级,输出图像占用n个灰度级,一般当n/m < 0.65时表明灰度级损失较大,需进行灰度补偿。
灰度补偿的原理是将经过变换函数映射后合并的灰度级分离出来成为独立的灰度级。为保证一定的对比度拉伸,从合并的灰度级中选择一部分作为分离对象。灰度补偿只对图像占用的灰度级进行操作,通过将映射后未取整的新灰度级进行等比例放大,例如映射后的2个相邻的灰度级8.1和8.5,同时乘以3,为24.3和25.5,则该合并的灰度级取整后得到分离;若2个相邻的灰度级8.1和8.2,同时乘以3,为24.3和24.6,则取整后仍不能分离。我们认为这2个灰度级可以合并以增大其他灰度级间差异,从而拉伸对比度。
合并的灰度级独立后,将占用一定的灰度空间,虽然总的灰度空间一定,但在映射后存在的新灰度中,有一部分相邻灰度级间存在一定的空白空间。例如输入图像存在灰度级5和6,映射后新灰度级为10和16,则灰度范围[11,15]即为空白空间。因此,分离合并灰度级所需空间可从空白空间中获得。对每部分空白空间根据其大小进行等比例压缩,为防止压缩过程中独立灰度级合并,当相邻灰度级空白空间为1时,对其停止压缩,例如新灰度级10和16在压缩过程中变为10和11时,就停止对该相邻灰度级的压缩。将选择的合并灰度级都分离出来后,就完成了灰度补偿,进而进行输出图像重构。具体操作步骤如下。
通过式(6)获得初步转换函数X,它的每个元素xk都是小数,取整后才能重构图像。而取整就会导致多个灰度级映射到一个灰度级,因此,为了选择性地保留灰度级,在对X中值取整前,分离要保留的灰度级,具体如下所示:
| $ \mathit{\boldsymbol{X'}} = \beta \times \mathit{\boldsymbol{X}}. $ | (18) |
式中:X′=[x′1, …, x′k, …, x′255]为扩大的灰度转换函数,其范围超过255;β为分离参数,β越大,保留的灰度级越多,过大会导致图像增强效果消失,经大量实验确定β一般取2~4。
在转换函数X′中,灰度级间的差距变大,定义相邻灰度级差向量G如下:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}} = \left[ {{g_{\left( {0,1} \right)}}, \cdots ,{g_{\left( {i,j} \right)}}, \cdots ,{g_{\left( {254,255} \right)}}} \right]}\\ {{g_{\left( {i,j} \right)}} = {{x'}_i} - {{x'}_j},j - i = 1} \end{array}} \right.. $ | (19) |
从式(19)得到相邻灰度级差向量G后,若G中的值小于1,则认定该相邻的2个灰度级可以合并,从而完成对需要保留灰度级的选择,然后在保证剩余灰度级独立的前提下对转换函数X′进行灰度级范围压缩。
首先获取压缩差值ΔK=max(X′)-max(X),以此对转换函数X′进行线性压缩。接着,将相邻灰度级差向量G中每个值减1保证分离的灰度级压缩后不会合并,为保证压缩差值的非负性,再将小于0的值置为0,最后根据压缩比例得到压缩差向量ΔG,表达式如下:
| $ \left\{ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{G}} = \mathit{\boldsymbol{G'}} \times \left( {\Delta K/{\rm{SUM}}\left( {\mathit{\boldsymbol{G'}}} \right)} \right)}\\ {\mathit{\boldsymbol{G'}} = \mathit{\boldsymbol{G}} - 1} \end{array}} \right.. $ | (20) |
其中,将G′中小于0的值置为0。根据ΔG得到压缩后的转换函数Y=[y1, …, yk, …, y255],计算如下:
| $ {y_k} = {{x'}_k} - \sum\limits_{i = 1}^k {\Delta \mathit{\boldsymbol{G}}\left( i \right)} . $ | (21) |
由此,获得在有效动态范围内进行灰度级补偿的转换函数Y,以此重构输出图像。
2 实验结果从公共库图片中选取大量不同场景的质量不好的彩色图像,对这些图像进行处理,采用HE算法、BBHE算法[10]、MMBEBHE算法[12]、LDR算法[14]和本文算法分别对其增强,进行效果对比,从主观视觉定性和客观参数定量两方面对增强结果进行评价。LDR算法中取α=5,本文算法中取β=2.5。
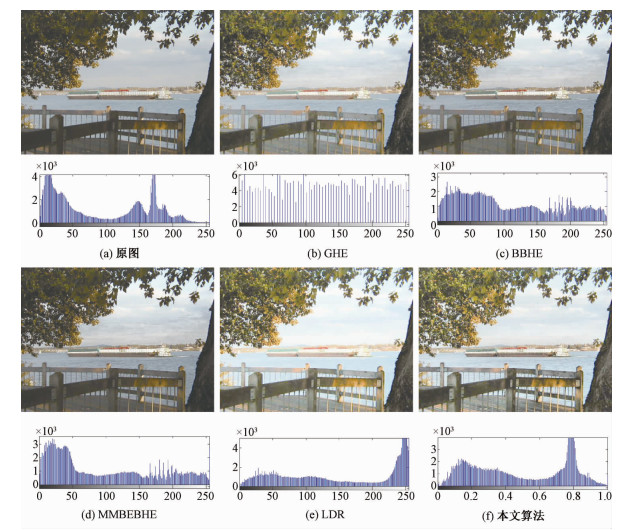
2.1 视觉效果分析采用上述算法的处理结果如图 3~图 8所示。从图 3中看出,GHE增强了图像的整体亮度,但图像的局部对比度减弱,图像变得模糊。BBHE虽然提升了一定的亮度和暗区对比度,但整体效果偏暗,MMBEBHE增强效果不明显,这两种算法结果都有一定的阴影痕迹,破坏了图像层次感。LDR算法整体亮度提高明显,暗区细节增强较好,但是亮区偏亮,细节减少,出现过增强。本文算法适当地提升了整体亮度和对比度,暗区细节得到增强,亮区细节得到保持,视觉效果良好。
|
Download:
|
| 图 3 河边场景增强结果以及各结果直方图 Fig. 3 Enhancement results and histograms of river scene | |

|
Download:
|
| 图 4 整体图中1、2局部处效果对比 Fig. 4 Comparison of the results in local parts 1 and 2 of the whole picture | |

|
Download:
|
| 图 5 建筑场景增强结果 Fig. 5 Enhancement results and histogram of architectural scene | |

|
Download:
|
| 图 6 大桥场景增强结果 Fig. 6 Enhancement results and histogram of bridge scene | |

|
Download:
|
| 图 7 树林场景增强结果 Fig. 7 Enhancement results and histogram of forest scene | |

|
Download:
|
| 图 8 海边场景增强结果 Fig. 8 Enhancement results and histogram of seaside scene | |
图 4给出图 3中的两处局部放大的对比结果,图 4(a0)给出整体图中的局部标记位置,标记1处的部分较暗,标记2处的部分较亮,可以观察亮区和暗区的局部细节增强情况。图 4(a1)~4(f1)为标记1处的各算法效果对比图,图 4(a2)~4(f2)为标记2处的各算法效果对比图。
从图 4(a1)~4(f1)看出,对于暗区部分,BBHE和MMBEBHE算法对暗区细节改善效果不明显,GHE、LDR和本文算法明显提升了暗区亮度,本文算法得到的局部细节视觉效果更好。从图 4(a2)~4(f2)看出,对于亮区部分,GHE、BBHE和MMBEBHE算法较好地保持了亮区细节,但出现明显的人工伪影,LDR算法结果中一部分亮区细节丢失,而本文算法在保持亮区细节的基础上取得了较好的视觉效果。
图 5~图 8增强结果表明,BBHE和MMBEBHE算法整体亮度增强不大,对比度增强效果不显著。GHE在亮度均匀场景下增强程度不大,暗图像过增强。LDR整体增强效果较好,暗区对比度增大,亮区有时过增强,图 5中亮区细节得到保持,但出现人工伪影。本文算法提升了整体亮度,增大暗区对比度和保持亮区视觉细节,达到了增强视觉效果的目的。
2.2 参数定量分析本文首先采用绝对平均亮度差(AMBE)和离散熵(DE)[16]作为定量评价指标。AMBE是增强前后图像平均亮度差值的绝对值,该值越小,表明图像亮度保持效果越好。DE表示图像所含的信息量,其值越大,表明图像的细节越多。
然而上述参数只是一种物理上的定量标准,与视觉效果并不一致,根据Weber定律,人眼能感受到的最小亮度差异与背景亮度成正比,这个最小亮度差为“恰可识别差异(JND)”,小于JND的差异是感受不到的。因此,结合上述的二维视觉差异直方图,本文提出一个反映人眼可感知差异的参数,即视觉感知差异(visual perceptual differences, VPD)。在一个8邻域窗口中,获取中心像素(i, j)与其他像素灰度差值,统计差值中大于该背景下JND的个数ωi, j,然后得到所有的ωi, j进行求和,进而得到参数VPD,公式如下:
| $ {\rm{VPD}} = \left( {0.5 \times \sum\limits_{i,j} {{\omega _{i,j}}} } \right)/W. $ | (22) |
其中,W为图像像素的个数。
表 1~表 3分别为上述图 3、图 5、图 6、图 7、图 8中实验图像得到的参数AMBE、DE、VPD的结果。从表 1看出,BBHE和MMBEBHE保持亮度效果较好,但偏暗图像亮度得不到提高。GHE保持效果不稳定,不同图像偏离程度不同。LDR提升整体亮度,但偏离较大。本文算法均值差比LDR小,既提升亮度,又防止图像过增强,整体视觉效果较好。
|
|
表 1 AMBE参数 Table 1 AMBE parameters |
|
|
表 2 DE参数 Table 2 DE parameters |
|
|
表 3 VPD参数 Table 3 VPD parameters |
表 2结果表明,GHE保持信息量的不稳定,对较暗图像信息增幅较大,对其他增幅较小,还会损失信息。BBHE和MMBEBHE有增加信息量的效果。LDR和本文算法增幅信息的效果更好,且本文算法较LDR基本更优。
表 3反映人眼可感知的信息量,结果显示,GHE视觉增强效果依旧不稳定。BBHE和MMBEBHE有一定的增强效果,BBHE效果更好。相比之下,LDR效果更为明显,视觉效果更佳。本文算法表现最好,较之前有较大提升,和视觉效果比较一致。
2.3 性能分析采用上述算法对图 3、图 5、图 6、图 7、图 8进行处理,比较各算法的平均运行时间,并且与多尺度Retinex(MSR)算法[4]进行比较,MSR算法已经可以应用于实时处理的领域。在主频2.53 GHz、内存2 GB、window 32操作环境下,采用Matlab 2011软件运行算法,运行结果如表 4所示。
|
|
表 4 各算法运行时间 Table 4 Average running time of algorithms |
从表 4看,本文算法运算效率虽然低于HE、BBHE算法,但是比可用于实时处理的MSR算法高,如果将本文算法用其他高效率的编程语言编写,则运行时间更短,从而满足快速处理要求。
3 结论本文结合视觉特性和灰度补偿技术,提出一种基于LDR的改进算法,该算法对公共图像库中不同场景、不同亮度的图像进行增强,取得较好的视觉效果。对增强结果进行视觉效果定性分析和参数定量分析,和多种算法进行对比,说明该算法对多种类型的图像都有较好的增强效果。该算法只涉及空域的简单计算,采用固定的参数,处理速度快,满足实时处理的要求。
| [1] |
Land E H. Recent advances in retinex theory and some implications for cortical computations:color vision and the natural image[J]. Proceedings of the National Academy of Sciences of the United States of America, 1983, 80(16):5163–5169.
DOI:10.1073/pnas.80.16.5163 |
| [2] |
McCann J. Lessons learned from mondrians applied to real images and color gamuts[C]//Colorand Imaging Conference. Society for Imaging Science and Technology, 1999(1): 1-8.
|
| [3] |
Jobson D J, Rahman Z, Woodell G A. Properties and performance of a center/surround retinex[J]. IEEE Transactions on Image Processing:A Publication of the IEEE Signal Processing Society, 1997, 6(3):451–462.
DOI:10.1109/83.557356 |
| [4] |
Jobson D J, Rahman Z U, Woodell G A. A multiscale retinex for bridging the gap between color images and the human observation of scenes[J]. IEEE Transactions on Image Processing:A Publication of the IEEE Signal Processing Society, 1997, 6(7):965–976.
DOI:10.1109/83.597272 |
| [5] |
Rahman Z, Jobson D J, Woodell G A. Multi-scale retinex for color image enhancement[C]//International Conference on Image Processing, IEEE, 1996(3): 1003-1006.
|
| [6] |
李云, 刘学诚. 基于小波变换的图像对比度增强算法研究[J]. 计算机应用与软件, 2008, 25(8):100–103.
|
| [7] |
Huang K Q, Wang Q, Wu Z Y. Natural color image enhancement and evaluation algorithm based on human visual system[C]//IEEE International Conference on Acoustics. 2006, 3: 721-724.
|
| [8] |
Yu Z, Bajaj C. A fast and adaptive method for image contrast enhancement[C]//International Conference on Image Processing, IEEE, 2004(2): 1001-1004.
|
| [9] |
Kim J Y, Kim L S, Hwang S H. An advanced contrast enhancement using partially overlapped sub-block histogram equalization[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2001, 11(4):475–484.
|
| [10] |
Kim Y T. Contrast enhancement using brightness preserving bi-histogram equalization[J]. IEEE Transactions on Consumer Electronics, 1997, 43(1):1–8.
DOI:10.1109/30.580378 |
| [11] |
Wang Y, Chen Q, Zhang B. Image enhancement based on equal area dualistic sub-image histogram equalization method[J]. IEEE Transactions on Consumer Electronics, 1999, 45(1):68–75.
DOI:10.1109/30.754419 |
| [12] |
Chen S D, Ramli A R. Minimum mean brightness error bi-histogram equalization in contrast enhancement[J]. IEEE Transactions on Consumer Electronics, 2003, 49(4):1310–1319.
DOI:10.1109/TCE.2003.1261234 |
| [13] |
Celik T. Two-dimensional histogram equalization and contrast enhancement[J]. Pattern Recognition, 2012, 45(10):3810–3824.
DOI:10.1016/j.patcog.2012.03.019 |
| [14] |
Lee C, Lee C, Kim C S. Contrast enhancement based on layered difference representation of 2D histograms[J]. Image Processing IEEE Transactions on, 2013, 22(12):5372–5384.
DOI:10.1109/TIP.2013.2284059 |
| [15] |
许欣, 陈强, 孙怀江, 等. 结合视觉感知特性的梯度域图像增强方法[J]. 计算机辅助设计与图形学学报, 2009, 21(1):130–135.
|
| [16] |
单建华, 何金洪. 基于人类视觉系统的动态直方图均衡算法[J]. 计算机科学与应用, 2013, 3(2):110–116.
|
 2018, Vol. 35
2018, Vol. 35 


