2. 中国科学院大学, 北京 100049;
3. 哈尔滨市勘察测绘研究院, 哈尔滨 150010
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Harbin Institute of Geotechnical Investigation and Surverying, Harbin 150010, China
2D/3D点包含关系,即二维空间中点与多边形及三维空间中点与多面体的相交关系判定,是计算几何、计算机图形学、计算机辅助制图(CAD)以及地理信息系统(GIS)等诸多学科领域的重要基础性问题之一[1]。以GIS为例,矢量多边形用作2D GIS面域实体的表示,而多面体能够一对一地描述任意复杂体对象(如带洞、孔、非流形等),故被越来越多的3D应用所采纳,例如文献[2-3]等。作为几何关系运算的基础算法,2D/3D点包含与多种GIS基本操作(如查询等)以及复杂空间分析算法(如集合操作、缓冲区分析、拓扑关系分析等)均密切相关[4]。点包含算法的正确性及效率因而将影响GIS的性能,2D/3D点包含算法的研究因此受到GIS界及相关学科的关注。
迄今为止,2D/3D点包含研究已经开展了较长时间,提出各种不同方法。在三维点包含中,大部分算法基于特定的预处理策略,例如面分层划分、凸空间划分、规则空间划分,以及等级空间划分(例如八叉树、BSP树等)[1, 5-8]。但是,此类预处理方式未能对“点与多面体”空间几何关系做出理论解析,且预处理计算本身需要一定的时间复杂度。非预处理方法包括角度法、四面体法及射线法[9-14]。角度法将多面体径向投影到以测试点为中心的单位球上,如果投影覆盖整个单位球,点在多面体内;否则,点在多面体外。四面体法将一个三角形网格表示的多面体分解成若干个四面体,并将体积符号化为(1,0,-1),通过累加包含测试点的四面体体积判定点包含关系。射线法相对简单,通过判定沿测试点发出的水平或垂直方向射线穿越多面体表面次数的奇偶特征确定包含关系。但射线法存在奇异性问题,即射线与节点重合、与多边形棱边共线,或子平面共面情形,若遇到奇异点需改变射线方向重新计算,求交时间将会相应增加。因此,学者们提出能够处理奇异点的方法,主要包括合成法向量法以及投影法[12, 15]。合成法向量法中的合成向量并不存在,缺乏严格的数理基础,数学上不严谨,会产生误判。投影法需要首先计算子平面法向量方向(即先计算子平面法向量),这不仅增加计算复杂度,也导致其不适合曲面多边形点包含关系判定,各种奇异点的投影及其叠加特征仍需系统、全面的几何解析。
在二维空间,点与多边形包含关系的判定常用方法包括环绕法(WN)及射线法(CN)两类[16-19]。环绕法根据多边形节点环绕测试点次数决定点包含关系,它能够适应自相交多边形的判定,且有较高的判定精度,但其效率相对较低。相比之下,算法简单的射线法是当前二维点与多边形关系相交判定的常用方法。但当前射线法(本文称为传统射线法)仍未能对射线与多边形关系做出完整的几何解析。传统射线法以多边形线段为基础,分别计算每条线段与射线相交关系,使每个节点与测试点的比较与计算次数达到2次。其实,射线以上(以下)的多边形各段边界节点的纵坐标值分别大于(小于)测试点y值,在横线上的节点等于测试点y值。据此可以分段处理以顺序筛选段内各节点,即增量筛选法,从而可大幅度提高计算速度。
Zhang和Zhang[13]推导子平面相交关系定理,这些定理对于提高点与空间子平面包含关系判定效率具有重要作用。为了证明正投影下这些定理仍然成立,本文首先简述赤平极射及其空间对象相交关系理论解析,然后导出广义赤平极射定理,从而建立赤平极射与正射投影的联系,使正射投影具有赤平极射性质,即赤平极射所建立的相交关系判定定理无需坐标变换,可直接应用于正射投影中。论文进一步对径向分界点进行分类,系统解析各类径向点(分界点、非分界点及不定点)在点圆中投影与叠加特征,并将3D转换为2D与水平射线以上(或以下)相交线段的筛选问题,进而设计2D增量筛选法,2D/3D点包含的计算效率全面提高。需要指出的是,本文证明过程以点与一般多面体为例,但对于曲面多面体仍然适用。
1 基本概念及定义1) 赤平极射投影及其空间对象相交关系理论解析,文献[13]在赤平极射下解析空间对象关系,这一理论对于指导点/体、点/面关系求交具有重要意义,本文首先对赤平极射及其空间对象相交关系解析做简述如下:
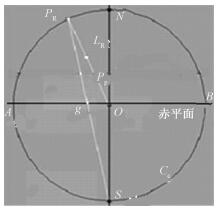
图 1为赤平极射投影示意图,LR为径向线,一个球体,其球心为O,半径为R,AB为穿过圆心的赤道平面(简称赤平面),S与N分别为球南极和北极点,Pp为空间点,从球心出发经过节点Pp的射线LR与球面相交于点PR(点Pp的球面投影),点PR与点S的连线交赤平面于点g,点g就是空间点Pp的赤平面投影,即三维坐标转换为赤平面下的二维坐标,详细见文献[13]。
|
Download:
|
| 图 1 赤平极射投影示意图 Fig. 1 Sketch map of stereographic projection | |
从赤平极射出发可准确解析空间对象相交关系:假定一个体状空间对象(即多面体),其最小包围球:圆心为O(也是多面体质心),半径为R,则多面体的所有节点和子平面都可投影到二维赤平面上,对于2个空间对象是否相交,则可通过首先判定其外包球是否相交,如果外包球相交,则可进一步判定多面体是否相交,如果相交,其交集必然在2个球的交集区域内。因此,可以以任一对象外包球的中心向球面做射线,称为径向线(简称LR,见图 1,本文中由公共点(节点)、查询点或检测点发出的射线也称为径向线),累计径向线与所有相交子平面的奇偶性,判定2个空间对象是否相交:奇数相交,偶数不相交。由于径向线子平面相交可能存在奇异点,有必要对各类奇异点进行分类解析。
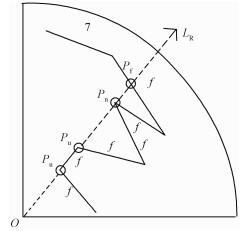
2) 各种分界点:径向线交多面体表面于点Pi(i=1, 2, 3, …, n),点Pi将射线分为两部分,δr邻域范围(δr邻域范围指没有遇到其他子平面的范围)内射线LR的两段对多面体的内、外属性有(见图 2,其中LR:径向线,O:最小外包球体的球心, Pf:分界点, Pn:非分界点, Pu:不确定分界点, f:多面体与径向线相交的平面):
|
Download:
|
| 图 2 不同分界点剖面图示意图 Fig. 2 Sketch map of various dividing points | |
A. 分属内、外两侧,则该点为径向分界点Pf;简称分界点;
B. 点的两侧不发生变化,同在多面体内(或体外),则该点为非径向分界点Pn,简称非分界点;
C. 一侧位于多面体表面上(包括棱边)上;另一侧位于多面体内或体外;该点的属性需根据环境判断,则该点为不确定径向分界点Pu,简称不定点。
3) π平面:由径向线作为平面法线、经过测试点Pc的平面,称为π平面。
4) 点圆:在π面上,以节点P的投影g为圆心、以微小δr为半径画圆。圆中不包含其他的节点和不经过点g的线段投影,则该圆称之为点圆。δr充分小,但δr≠0。
5) 子平面、同点子平面、同点棱边:由多条线段围成的、封闭的、有界的平面称为子平面;多面体表面与某一节点(也称为公共点)连接的所有子平面,称为同点子平面;多面体表面棱边与某一节点连接的所有棱边,称为同点棱边。
6) 最小包含球(简称小球):以空间对象任意点为球心、以微小δr为半径做球。在小球范围内,除作为球心的“点”(注:是“点”,不是“节点”。因为小球的球心可能不是节点)、过球心的同点棱边和同点子平面外,不存在任何其他的节点、棱边和子平面,满足这样条件的球体,称为小球。小球的半径δr充分小,但δr≠0。对于曲面,当小球缩小时,不能成为任何曲面的密切球。降维后,小球称为点圆。因此,点圆缩小时,不可能成为任何线段的密切圆(或曲率圆)。
7) 投影扇:在点圆内由圆心发出的2条射线、和这2条射线切割点圆形成的弧段围成的闭区域称为投影扇。
2 各种分界点的投影及叠加性质 2.1 基本性质判定定理2.1 分界点在点圆中扇的投影层数,均为奇数层。非分界点或均为偶数层;或部分为偶数层、部分为空。不定点部分为奇数层、部分为偶数层;或部分为奇数层、部分为空;或部分为奇数层,部分为偶数层,部分为空。见表 1中投影图。
|
|
表 1 同点子平面在点圆中的投影 Table 1 Facets with the same node and their projections on point circle |
证明 设:π平面上点圆中公共点Pc为圆心,临域点为Pr,过点Pr做射线N’,与过点Pc的射线N平行(见图 3(b),图中示例性显示与射线相交的三层子平面);射线上距离Pr最远的子平面为Sf、最近的子平面为Sn。过点Pr的射线与Sf交于点Psf、与Sn交于点Psn。Pri为位于各投影扇中非边界的点,投影扇投影层奇偶组合共有以下几种情况:

|
Download:
|
| 图 3 射线(径向线)点圆投影及其三维图 Fig. 3 Projection of the ray (i.e., radial line) on point circle and the three dimensional diagram | |
1) 各投影扇中投影层数均为奇数
Psf、Psn沿射线相向移动δl(δl充分小,但δl≠0,不穿越另一子平面,图 3(a),移动后Psf、Psn间距离减小,2点分别属于多面体内、外,这一点业内已经作为公理使用。因所有扇均为奇数层投影,当lim Pri→Pc时(见表 1中投影图),Pc=Pri(PointC=Paritri),点的径向线两侧分别在多面体内、外,根据定义Pc为分界点。
2) 投影扇投影层数均为偶数层:证明与上类似。
3) 投影扇投影层部分为奇数层,部分为偶数层,部分为空:
由上述分界点与非分界点证明可知,当limPru→Pc(u=i, j)时,必有Pri≠Prj,投影奇偶属性不同(见表 1中投影图),极限不相等,Pc既不是分界点,也不是非分界点,因此只能是不定点。证毕。
2.2 投影叠加性质多面体上不定点总是成对出现的,称为不定点对:
定义:不定点对具有径向分界点性质,称为径向分界点对,简称分界点对;具有非经向分界点性质,称为非径向分界点对,简称非分界点对。
判定定理2.2 奇数个分界点叠加为分界点,偶数个分界点叠加为非分界点。
证明 因分界点各部分投影均为奇数,所以奇数分界点叠加后,各投影扇仍为奇数层,根据表 1是分界点;同理,偶数个分界点叠加后为偶数层,是非分界点。
判定定理2.3 分界点与非分界点叠加后为分界点;非分界点叠加仍为非分界点。
证明 与上述类似。
判定定理2.4 不定点对若为分界点对时,则只有一个分界点。当为非分界点对时,分界点数或为“0”;或为“2”。
由此可以得出:对于不定点对,分界点的数量可能是0、1、2,因此,简单擦除不定点对,可能产生误判。简单擦除不定点对是由于只考虑非分界点对,未考虑分界点对的原因。由叠加判定定理2.1、判定定理2.2得出:
推理:各分界点单独投影后判定查询点性质,与所有各种分界点综合投影后判断查询点的性质相同。
推理结论很重要,所有各种分界点的投影,综合叠加投影后判断,软件编制简单,速度快,避免了不定点叠加投影。再根据各投影层奇偶性相等的性质,不用对所有投影扇全部投影,只对其中任意一个投影,判断其奇偶性即可得出查询点的性质。若综合投影扇投影层数为奇数,查询点在多面体内;投影层为偶数,查询点在多面体外。
筛选过程中,若遇到查询点与子平面共面、且子平面投影包含点的投影时,根据广义赤平极射原理,改变投影方向判断点与该子平面关系。
子平面只能包含、但不能切割投影扇弧段,即子平面投影只能整体包含投影扇。若子平面包含投影扇,该扇投影层数累加1。
2.3 二维投影性质三维空间算法在特殊情况下可转化为二维算法,二维求交问题是三维问题的退化。若多面体为柱状、径向线垂直于柱的轴线,用柱的轴线作为法线的平面切割多面体、射线位于π平面上,多面体表面在π平面上成为Polygon,点圆内为射线两侧的两条线段。在二维情况下,射线与Polygon边界相交有以下几类情况,即点圆退化的情形:
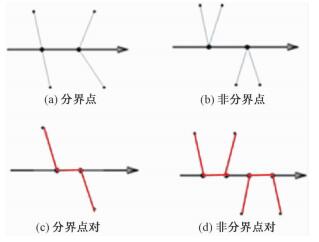
1) 分界点:①射线穿越线段,射线与线段有交点;②射线与节点相交,与节点相连的两条线段另一端点分列射线两侧。如图 4(a), 若交点下x坐标大于查询点x坐标, Pf累计1;
|
Download:
|
| 图 4 点类型 Fig. 4 Point types | |
2) 非分界点:射线与节点相交,与节点相连的两条线段另一端点位于射线同一侧。如图 4(b)所示,若交点下x坐标大于查询点x坐标, Pf累计1;
3) 分界点对:射线与线段相交,离开射线的两条线段另一端点分列射线两侧。如图 4(c)所示,若交点下x坐标大于查询点x坐标, Pf累计1;
4) 非分界点对:射线与线段相交,离开射线的两条线段另一端点在射线同一侧(或上侧、或下侧)。如图 4(d)所示,交点下x坐标均大于查询点x坐标, 且线段都在上侧,Pf累计2,否则不累加。注:分界点数累加2或不累加(累加0)对测试点内外属性的判定无影响,因此为非分界点对。
当子平面垂直投影面时,投影为一直线段。若该线段与射线重合,所有点都在射线上,没有其他点离开射线。根据定理2.1,无论是分界点还是非分界点,点圆内各投影扇中的投影层数均相等;又根据推理,综合投影与个别投影后再判断查询点性质结论相同。因此,2D情况只计入射线以上或射线以下一部分投影判断即可。由此推理得:
判定定理2.5 从查询点开始,射线以上(或射线以下)与射线相交的线段投影层数为奇数层,查询点在Polygon内,为偶数层,查询点在Polygon外。如图 5(a)所示,满足这样条件的多边形的线段有3条(奇数),分别是P2P3、P61P62、P70P71,即分界点数量为3,查询点Q位于多边形内。Q(xq, yq)为测试点;Li (i=1, …, 7)为第i条段,其中,P2, k (k=2, …, 28)为第3段(L3)内节点, 即段内增量;P2, 1即(节点P3)为该“段标识增量”。所要指出的是,这里增量的概念源于增量方程dS=m·dx+n·dy,因为射线法线单位向量(m, n)=(0, 1),故dS=dy,即节点与射线的增量就是节点域射线纵坐标之差。证明同判定定理2.1。若节点在射线上,即多边形线段与投影圆在同一平面上,改变投影方向,即将点圆垂直与射线判定。
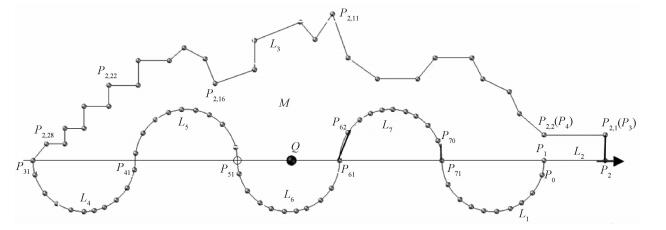
|
Download:
|
| 图 5 多边形(M)分段筛选 Fig. 5 Segment filtering of polygon (M) | |
根据投影性质以及判定定理2.5,可构建点与多边形包含关系高效判定算法——增量筛选射线法(IFCN)。算法简述如下:若多边形与射线R相交,形成n段(Li, i=1, …, n),其中任何一段Li可能位于射线之上(所有点y值均大于查询点yp)、射线之下(均小于yp)、或恰好位于射线上(均等于yp)。IFCN增设段标识增量作为比对种子;筛选段内增量(节点),筛选出射线以上(或射线以下)与射线相交、且x值大于(或小于)查询点x值的线段,该类线段数量的总和就是射线穿越的分界点数量,提高筛选速度。段标识增量(Pi, 1)是指每段离散曲线离开射线后的第1个节点(图 5(a)中P2, 1在第3段L3),段内增量(Pi, k)是离开射线后的第k(k≠1)个点。段L3中的P2, 2, P2, 3, …等节点,该段上所有点y均大于测试点的yq。段标识增量共有两种情形:一种是在射线以上,另一种是在射线以下。对大数据集对象理论上讲增设段标识增量后,一般每次只需比较段内增量一个y坐标值,而传统射线法(CN)以多边形线段为单位,检测每条线段是否与射线相交,因而线段上2点和查询点的y值做2次比较运算,因此,与CN算法相比,IFCN通过筛选,可节约计算时间50%。下面给出IFCN算法的伪代码:
交点横坐标相对位置函数
int getT(double x, double xq, int mli)
输入:
xq:查询点横坐标
x:线段与查询点所在横线交点的横坐标
mli:水平线段值方向,与x轴方向同向为1,反向为-1
输出:与x轴的交点相对查询点的位置(查询点的正向、负向,或与查询点相交)
IF (mli=1){IF(x>xq)返回1;ELSE IF(x < xq)返回-1; ELSE返回0;}
ELSE IF (mli=-1){IF(x < xq)返回1; ELSE IF(x>xq)返回-1; ELSE返回0; }
返回0;
增量筛选射线法(IFCN)求交函数:
输入:q(xq, yq)查询点,顺序输入多边形边界点POINT p[i], 其中i=0, 1, …, nPoints (节点数),
输出:查询点与Polygon的关系(外:0,内:1,与节点重合:2,位于线段上:3)
//初始化
IF (第一个点p[0].y>yq)段标识增量在射线以上,ifcn01 (段标识增量)> yq
ESLE IF(p[0].y < yq)段标识增量在射线以下,ifcn01 < yq
ESLE IF (p[0].y=yq)第一点在射线上
IF (p[0].x> xq) mli=1
ESLE IF (p[0].x < xq) mli=-1
ESLE查询点q与边界点重合, 返回2
循环(筛选并确定段标识增量ifcn01:顺序查找不在横线y=q.y上的第一个节点p[j])
IF (p[j].y>yq)段标识增量在射线以上,ifcn01>yq
IF (p[j-1].x>xq) pf (径向分界点数量)累加1,跳出循环
ELSE IF (p[j].y < yq)段标识增量在射线以下,ifcn01 < q.y,pf不累加,跳出循环
ELSE:筛选在横线y=yq上的点
t=getT(p[j].x, xq, mli)
IF (t=0)查询点与边界点重合返回2
ELSE IF (t < 0)查询点在边界线上 返回3
IF(如果没有找到不在横线上节点(y=yq))
查询点与Polygon不相交,返回0
//遍历筛选
循环1(遍历其余)
IF(ifcn01 >yq)
循环2(遍历段内增量(ifcn02))
IF(p[k].y>yq)继续遍历、筛选下一节点;
IF(p[k].y < yq)该线段与射线相交,并穿越了射线, 计算线段与射线交点x
ifcn01 < yq段标识增量
IF (x>xq) pf累加1,跳出循环2
ELSE IF (x < xq) pf不累加,跳出循环2
ELSE查询点在边界线上,返回3
IF(p[k].y=yq):点p[k]在射线上
pf累加1
IF(p[k].x>xq) mli=1
IF(p[k].x < xq) mli=-1
IF(p[k].x=xq)点与Polygon节点重合,返回2
循环3(顺序查找不在横线y=yq上的节点,确定段标识增量ifcn01)
IF (p[j].y>yq) ifcn01 >yq,pf累加影加1,跳出循环3、2,继续筛选
IF (p[j].y < yq) ifcn01 < yq,pf不累加,跳出循环3、2,继续筛选
IF (p[j].y = yq)
t=getT(p[j].x, xq, mli);
IF(t=0)查询点与边界点重合, 返回2
IF(t < 0)查询点在边界线上, 返回3
IF(ifcn01 < yq)
类似上述ifcn01 >yq情形的处理上,循环筛选……
IF (pf为奇数) 点在Polygon内,返回1
IF (pf为偶数) 点在Polygon外,返回0
3.2 点圆三维点包含判定算法—PC3D因检测点是否在体内,与射线方向无关,且该理论算法无奇异情况存在,支持任何方向,故选择计算量小的方向作为径向线方向。下面给出在Oxy面上的点圆三维点包含判断方法(PC3D):查询点为Q(xq, yq, zq),垂直射线(径向线)方向为N→(0, 0, 1)(平行于z坐标轴),筛选大于、等于zq(查询点z坐标)的各种分界点,计算其次数。根据文献[13]中定理8“两子平面相交,其在投影面上的投影必然相交”;同样,查询点Q在Oxy面上的像Qp及其子平面投影Polygon相交,才可进入下一步判定,由此则可筛选掉大量无关子平面。算法简述如下:
1) 遍历筛选子平面;若子平面边界点在Oxy坐标面上的投影与查询点Q’的投影不相交,继续检测下一子平面;若相交,进行下一步;
2) 对投影包含查询点投影的子平面:
① 计算子平面系数m、n、p、S;
② 若p≠0(子平面在Oxy面上的投影为一多边形):
a 计算射线与子平面交点的高程z;
b 若该高程与查询点高程相同z=zq:按返回相交类型,确定查询点在多面体表面相交位置(子平面表面、棱边、节点),终止查询;
c 若小于查询点高程z < zq:返回步骤“1”,继续筛选;
d 若大于查询点高程zh>zq:如图 6所示,若线段与水平射线(平行于x轴射线)线相交、交点x坐标xp>q.x (线段与水平射线相交于P,且有一节点Pi位于射线上方),且线段另一端点Pi(xi, yi)的yi>yq,垂直射线相交次数pf累加1,否则不累加;返回步骤“1”,继续筛选下一子平面;
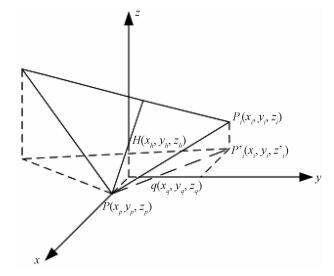
|
Download:
|
| 图 6 三维点包含测试示意图 Fig. 6 Sketch map of three dimensianal point inclusion test | |
③ 若p=0(子平面在Oxy面上的投影为一线段):
a 选择平面系数m≠0、n≠0的坐标面上判定,若点落子平面投影中,按返回类型判断相交位置,终止查询;
b 若不相交,返回步骤“1”,继续筛选;
3) 垂直径向线相交次数pf:若为奇数查询点在体内,偶数查询点在体外。
这样,查询点与多面体的关系(点在体内,或体外),除计算平面系数外,其他方法完全都是在二维条件下进行的,似乎是二维计算,但又确实是立体判断。
3.3 算法测试实验本实验对二维IFCN算法的效率以及三维包含算法的正确性进行测试。测试环境为:1)硬件:处理器Intel Pentium 4 630 3.00 GHz; 内存:2 GB;2)操作系统:Microsoft XP,Professional 2002;3)软件:Microsoft Visual Studio 2005 C++。
3.3.1 IFCN与传统CN算法效率对比二维IFCN算法测试所采用的数据是2000年吉林、黑龙江两省1:10万土地利用矢量数据。分别从中随机选取13类点数各异的多边形,其点数分别为5, 6, 7, 8, 10, 50, 100, 500, 1千, 5千, 1万, 5万,10万个。每类各选5个,共计65个多边形。分别在其MaxMin包围盒中随机生成1万个测试点,分别测试时间,然后与传统射线法做比较。计算与传统方法的计算时间百分比,即各组计算时间均值除以相应传统射线法的计算时间。跟传统CN算法相比,多边形的点数越多,IFCN的优势越明显,当多于100个点以上时,IFCN的计算耗时低于传统CN的40%。但少于10个点时,IFCN耗时略高一些,但最多不会增加10%的计算时间。筛选原理可专门设计针对由大量三角形构成的多边形包含算法:首先进行三角形筛选,然后进行三角形高效点包含测试,如同本文中的下一例子所述。
3.3.2 点圆三维包含算法(PC3D)测试该实验采用斯坦福大学构建的由三角形面片组成的3D模型(Bunny, Horse, Dragon)。并采用由Tao Ju开发的开源软件Polymender,对模型进行修复,使其形成封闭流形数据。表 2给出各模型基本数据信息,以及求交时间及内存资源占用信息,并与文献[12]的Kalay的投影法投影法(简称PJ)进行对比。
|
|
表 2 点圆求交(PC3D)及Kalay的投影法(PJ)测试结果 Table 2 Testing results of PC3D and Kalay's projection method (PJ) |
因模型投影到Oxy坐标面上后,众多三角形位于射线两侧,少数与射线相交,只有极少部分三角形才可能包含查询点(xp, y, zp),故可筛选掉无关三角形。以Dragon为例,筛选后求交耗时不足整个求交的5%。上述筛选后调用IFCN,如果相交,求子平面方程系数,并求解垂直径向线与子平面交点高程z,只有大于zp的分界点做累加,最后总的分界点数量进行点包含关系判定,整个计算效率极高。
4 结束语本文通过解析不同类型点在投影圆中的投影及其叠加特征,将复杂的点与任意多面体(包括流形、非流形、含洞、孔等)包含关系的判定转化为:与射线相交的2D线段筛选与累加计算,即三维问题降维成二维处理(在计算过程,除子平面系数计算外,与二维完全一致)。同时,通过广义赤平极射的理论导出,使正投影具有赤平极射的理论依据,赤平极射下解析的对象相交定理在正投影下仍然成立,如赤平极射解析下的定理8:“空间对象相交其在投影面上的像必然相交”可应用于正投影,故可在投影面上筛选掉大量测试点与子平面投影不相交的子平面,只有投影相交的子平面才计算平面参数,判定共面后才确认相交,这样可避免大量无效计算;同时增量筛选法也极大提高了投影面上点与多边形相交判定。另外,由于运算结果和投影扇排列次序无关,该方法适合并行计算与新型多核、集群计算环境。因此本文系统构建满足多种应用环境、支持任何径向、无需专门进行奇异点处理的点与多面体包含关系精确、高效判定理论与方法。它不仅适合离散子平面,同样适合曲面多面体。
基于点圆理论的二维/三维点包含算法高效、精确,内存资源量少与计算时间均远小于Kalay等方法,适合地理信息系统大规模、海量集数据的计算应用。无奇异点,是质的改变;增量筛选大幅度提高计算效率,是量的改变。
点圆退化后,二维求交,仍可使用二维点与任意多边形的关系判定,即位于射线之上(或之下)与射线相交,且交点x坐标大于测试点x坐标的多边形线段筛选与累加,然后判定其奇偶特征即可。据此我们建立点与任意多边形高效判定的增量筛选射线法IFCN,准确解析段标识增量(即多边形中离开射线的第一个节点)及其后各点(段内增量)的几何特征:段标识增量若位于射线之上,则段内增量y坐标大于测试点的yp,相应多边形各边只需测试一个节点的纵坐标,便可实现段内增量的循环筛选,即While (p[k].y)>yp) continue。而传统方法则需要每条边2个节点的y坐标都需要与yp做比较运算,即每个节点需重复计算2次。因此,从理论上分析IFCN可提高计算效率近50%。多边形节点数量越多、IFCN优势越明显。但节点数量小于10个时,IFCN不占优势。增量筛选法的实质就是通过几何关系的解析,筛选掉多余的空(无效)计算另外,针对点与大量三角形关系判定,IFCN可设计有针对性的高效算法:即首先筛选无关三角形,即只判断与射线相交的三角形,筛选掉无相交关系三角形,然后进行点与三角形包含关系判定。除增量筛选射线法IFCN外,还可设计增量筛选环绕法IFWN。IFCN与IFWN各有特色,可实现优势互补,其中IFCN判定效率更高,而IFWN则更为精确,对于距离射线距离近点的包含判定,往往需要IFWN完成,基于这两类算法,作者团队已研发了高精效的海量、复杂多边形叠加(相交)算法与软件,限于篇幅,后续论文将对此做深入讨论。
| [1] |
Wang W, Li J, Sun H, et al. Layer-Based Representation of Polyhedrons for Point Containment Tests[J]. IEEE Trans Vis Comput Graph, 2008, 14(1):73–83.
DOI:10.1109/TVCG.2007.70407 |
| [2] |
Arens C, Stoter J E, Oosterom P V. Modelling 3D spatial objects in a geo-DBMS using a 3D primitive[C]//IEEE International Conference on Computational Intelligence in Robotics and Automation. IEEE Press, 2009: 441-444.
http://dl.acm.org/citation.cfm?id=1650556 |
| [3] |
Penninga F, Oosterom P V. A simplicial complex-based DBMS approach to 3D topographic data modelling[J]. International Journal of Geographical Information Science, 2008, 22(7):751–779.
DOI:10.1080/13658810701673535 |
| [4] |
Gomboš I M, Žalik B. Point-in-polygon tests for geometric buffers ☆[J]. Computers & Geosciences, 2005, 31(10):1201–1212.
|
| [5] |
Chazelle B, Dobkin D P. Detection is easier than computation (Extended Abstract)[C]//12th ACM Symposium on Theory of Computing. ACM, 1980: 146-153.
|
| [6] |
Dietzfelbinger M, Karlin A, Mehlhorn K, et al. Dynamic perfect hashing: upper and lower bounds[C]//Foundations of Computer Science, 1988. Symposium on. IEEE, 1994: 524-531.
|
| [7] |
Bajaj C L, Dey T K. Convex Decomposition of Polyhedra and Robustness[J]. Siam Journal on Computing, 2006, 21(2):339–364.
|
| [8] |
Cui S, Fu X. Point in polyhedra test with direct handling of degeneracies[C]//The Joint Isprs Workshop on 3D City Modelling & Applications, the 6th 3D Geoinfo Conference, 2011: 91-97.
http://www.airitilibrary.com/Publication/Index?DocID=WFHYXW453037 |
| [9] |
Lane J, Magedson B, Rarick M. An efficient point in polyhedron algorithm[J]. Computer Vision Graphics & Image Processing, 1984, 26(1):118–125.
|
| [10] |
Feito F R, Torres J C. Inclusion test for general polyhedra[J]. Computers & Graphics, 1997, 21(1):23–30.
|
| [11] |
Ogayar C J, Segura R J, Feito F R. Point in solid strategies[J]. Computers & Graphics, 2005, 29(4):616–624.
|
| [12] |
Kalay Y E. Determining the spatial containment of a point in general polyhedra[J]. Computer Graphics & Image Processing, 1982, 19(4):303–334.
|
| [13] |
Zhang S, Zhang J. Theoretical analytics of stereographic projection on 3D objects' intersection predicate[J]. International Journal of Geographical Information Science, 2010, 24(1):25–46.
DOI:10.1080/13658810802687327 |
| [14] |
李新友. 一种实用的点/多面体分类算法[J]. 计算机辅助设计与图形学学报, 1991, 3(3):25–28, 24.
|
| [15] |
Khamayseh A, Kuprat A. Deterministic point inclusion methods for computational applications with complex geometry[J]. Computational Science & Discovery, 2008, 1(1):015004.
|
| [16] |
Kai H, Agathos A. The point in polygon problem for arbitrary polygons[J]. Computational Geometry, 2001, 20(3):131–144.
|
| [17] |
王文成, 吴恩华. 判断检测点是否在多边形或多面体内的新方法[J]. 软件学报, 2000, 11(12):1614–1619.
|
| [18] |
李维诗, 李江雄. 平面多边形方向及内外点判断的新方法[J]. 计算机辅助设计与图形学学报, 2000, 12(6):405–407.
|
| [19] |
王志强, 肖立瑾, 洪嘉振, 等. 多边形的简单性、方向及内外点的判别算法[J]. 计算机学报, 1998, 21(2):183–187.
|
 2018, Vol. 35
2018, Vol. 35