2. 北京交通大学理学院, 北京 100044
2. School of Science, Beijing Jiaotong University, Beijing 100044, China
1954年,排空效应(depletion)第一次被Oosawa和Asakura[1]提出。排空效应是基于体积排斥效应,设想胶体体系中含有两种直径相差很大的胶球,大球数量少体积大,小球数量多体积小。物质的自由能是F=E-TS,E是内能,T是温度,S是熵,对于软物质来说,内能E比TS小很多,在热平衡条件下自由能主要由熵S来决定,而小球对熵起主要贡献。在大胶球周围有一层排空层(depletion layer)不容许小球进入。当两个大胶球彼此靠近时,其排空层产生重叠的部分v,小球因此获得额外的自由体积v来运动,这导致小球的熵增,体系自由能的下降。在小球熵的驱动下,大球有团聚或靠近容器壁的倾向。这样的体积排斥被称为排空效应。
胶体排空作用在自组装结构制备、胶体系统稳定性调控等方面有着重要的应用,因而一直是理论、模拟和实验的研究者们关注的研究热点。在理论模拟领域,尽管对排空力的精确求解是相当困难的,但研究者们仍做了许多工作。有研究者使用直接模拟的接受比率法,计算台阶附近的排空相互作用[2]、硬墙对于一个椭球的排空力与排空力矩[3]、硬棒胶体对于胶体球的排空相互作用[4]。有研究者使用直接模拟方法的Wang-Landau方法,模拟计算椭球之间的排空力[5]。相对于定量计算的精确求解,还可以通过定性近似得到许多有意义的排空物理图像:用Asakura-Oosawa (AO)近似可以得到胶球在弯曲表面(凸面和凹面)附近的排空效应[6],通过Derjaguin近似可以得到小球与大球都具有排空层时大球的排空相互作用[7-10],细棒胶体在硬墙之间的排空相互作用[4, 11-13],薄盘胶体在硬墙之间的排空相互作用[14-17]等。实验上对于排空效应的探讨在文献[18]中也已经有很详细的介绍。
在之前的理论模拟中,无论是大球、小球还是墙平面,所有的研究对象都是坚硬的。因为对于模拟计算来说,硬颗粒间的相互作用更加简单清晰易于建模。而在实际的工业生产和日常生活中,胶体中的颗粒以软胶球居多,例如牛奶中的蛋白质胶球。因此我们想要对软胶球的排空相互作用进行探究,研究当体系中的大颗粒、小颗粒还有墙平面都是软结构时的排空相互作用。我们采用自洽场方法(SCFT:self-consistent field theory),以由A均聚物和AB二嵌段共聚物组成的共混物为研究对象。A和AB具有相同的链长N,体系中AB的浓度刚好达到临界胶束浓度(CMC:critical micelle concentration),多个AB高分子会自组装成以B嵌段为核心、A嵌段为外壳的AB胶束,可以被看作是大颗粒软胶球,而单个的A高分子会缠结成为A链团,可以被看作是小颗粒软胶球。此外,体系中还有一块高分子无法穿过的坚硬衬底平面,并且平面可以带上选择性。当平板带上对A组分的选择性时,会吸引体系中A均聚物,形成A软膜层;而当平板带上对B组分的选择性时,会吸引体系中的AB二嵌段共聚物,形成AB高分子刷软膜层。通过调控平板选择性,可以探究软胶球与不同软平面间的排空相互作用。
1 模型与理论本文中考虑由二嵌段共聚物AB在均聚物A溶剂中形成的球状胶束和一个平面衬底间的排空相互作用。AB是不对称二嵌段共聚物,A嵌段较长,长度分数为pA=0.7(pB=1-pA)。并且AB和A具有相同的链长N。当共聚物AB的浓度达到临界胶束浓度时,就会在溶液中形成以B嵌段为核心,以A嵌段为外壳的胶束,半径为0.8
|
Download:
|
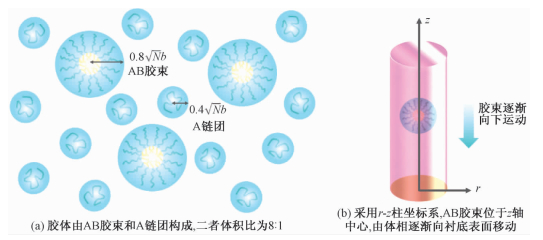
| 图 1 理论模型 Fig. 1 Theoretical model | |
取一个AB胶束作为研究对象,使用柱坐标系r=(r, z),将AB胶束中心放置在z轴上(图 1(b)),则胶束相对于z轴具有旋转对称性。除胶束外其他位置均填充溶剂A,可看作大颗粒胶束AB周围充斥着小颗粒链团A。将圆柱底部设为衬底硬表面,无法被聚合物分子穿透,因此在表面附近时总密度逐渐趋于零。因此,定义表面附近的总密度ϕ0分布
| $ {\phi _0}\left( {r,z} \right) = \left\{ {\begin{array}{*{20}{l}} 1&{\tau < z < Nz}\\ {{\rm{tan}}{{\rm{h}}^2}\left( {\frac{{2\tau z}}{{{\tau ^2} - {z^2}}}} \right)}&{0 \le z \le \tau } \end{array}} \right., $ | (1) |
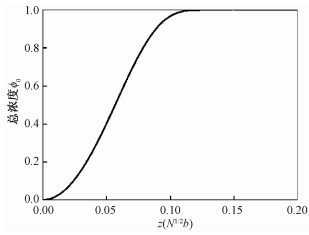
聚合物总密度ϕ0除表面附近之外均为1,在靠近表面的短距离τ内从1迅速减小到0。这里τ是表面层的特征长度,τ=0.15
|
Download:
|
| 图 2 接近表面处的总浓度曲线 Fig. 2 Total concentration curve near the surface | |
底部硬表面同时对于A/B组分具有选择性,并能够通过选择性吸附改变表面结构形成软膜层。定义表面场为H(r, z),其作用范围也为τ
| $ H\left( {r,z} \right) = \left\{ {\begin{array}{*{20}{l}} 1&{\tau < z < Nz}\\ {\mathit{\Lambda }\left( {1 - \frac{z}{\tau }} \right)}&{0 \le z \le \tau } \end{array}} \right.. $ | (2) |
常数Λ代表表面的选择性,当Λ>0时(即平板H>0),代表对A单体有吸引力,排斥B单体;当Λ < 0时(即平板H < 0),则代表对B单体有吸引力,排斥A单体;当Λ=0时,表面不具有选择性,是中性的。
将AB胶束的初位置放置在距离平板4
采用自洽场方法进行计算,体系体积为V。将AB和A看作高斯链,它们具有相同的链长N,且都具有不可压缩性,二者的单体体积统一为ρ0-1,单体长度统一为库恩长度b,采用
| $ {\mu _{\rm{c}}} = {\rm{ln}}\frac{{\phi _{\rm{c}}^{{\rm{bulk}}}}}{{1 - \phi _{\rm{c}}^{{\rm{bulk}}}}} + {\rm{ }}{p_{\rm{B}}}\chi N(1 - 2{p_{\rm{B}}}\phi _{\rm{c}}^{{\rm{bulk}}}). $ | (3) |
在自洽场框架下,链间相互作用由一个理想高斯链与多链相互作用产生的有效平均场之间的相互作用代替。哈密顿量可以由局域密度场{ϕ}和共轭场{ω}来写出:
| $ \begin{align} & \frac{NF}{{{k}_{\text{B}}}T{{\rho }_{0}}}=\iint{2\pi r\text{d}r\text{d}z\left[ \chi N{{\phi }_{\text{A}}}\left( r,z \right){{\phi }_{\text{B}}}\left( r,z \right) \right]}- \\ & \iint{2\pi r\text{d}r\text{d}z}\left[ {{\omega }_{\text{A}}}\left( r,z \right){{\phi }_{\text{A}}}\left( r,z \right)+{{\omega }_{\text{B}}}\left( r,z \right){{\phi }_{\text{B}}}\left( r,z \right) \right]- \\ & \iint{2\pi r\text{d}r\text{d}zH\left( r,z \right)}\left[ {{\phi }_{\text{A}}}\left( r,z \right)-{{\phi }_{\text{B}}}\left( r,z \right) \right]- \\ & \iint{2\pi r\text{d}r\text{d}z\xi \left( r,z \right)}\left[ {{\phi }_{0}}\left( r,z \right)-{{\phi }_{\text{A}}}\left( r,z \right)-{{\phi }_{\text{B}}}\left( r,z \right) \right]- \\ & {{z}_{\text{c}}}{{Q}_{\text{c}}}-{{Q}_{\text{h}}}. \\ \end{align} $ | (4) |
式中:第1行是分子间的相互作用能;第2行是密度场与共轭场的耦合能;第3行是表面相互作用能,其中H(r, z)是表面面场;第4行是不可压缩性条件,通过引入拉格朗日乘子ξ(r, z)保证局部的总密度固定为φ0(r, z);第5行是由单链配分函数体现的构型熵,Qc、Qh分别对应于共聚物和均聚物的单链配分函数。共聚物单链配分函数为Qc=∫∫drdzqc(r, z, s)qc+(r, z, s),其中s是由链长归一化的链围线长度,可以从0取到1;qc(r, z, s)和qc+(r, z, s)是末端积分传播子,分别满足如下修正的扩散方程:
| $ \begin{align} \frac{\partial }{\partial s}{{q}_{\text{c}}}\left( r,z,s \right)=&\frac{1}{6}N{{b}^{2}}{{\nabla }^{2}}{{q}_{\text{c}}}\left( r,z,s \right)- \\ &\omega \left( r,z \right){{q}_{\text{c}}}\left( r,z,s \right), \\ \frac{\partial }{\partial s}q_{\text{c}}^{+}\left( r,z,s \right)=&-\frac{1}{6}N{{b}^{2}}{{\nabla }^{2}}q_{\text{c}}^{+}\left( r,z,s \right)+ \\ &\omega \left( r,z \right)q_{\text{c}}^{+}\left( r,z,s \right). \\ \end{align} $ | (5) |
外场的形式如下:
| $ \omega \left( r,z \right)=\left\{ \begin{array}{*{35}{l}} {{\omega }_{\text{A}}}\left( r,z \right) & 0<s<{{p}_{\text{A}}} \\ {{\omega }_{\text{B}}}\left( r,z \right) & {{p}_{\text{A}}}<s<1 \\ \end{array} \right.. $ | (6) |
传播子的初始条件分别是qc(r, z, 0)=1和qc+(r, z, 1)=1。均聚物单链配分函数Qh=∫∫drdzqh(r, z, 1),其中qh(r, z, s)是均聚物末端积分传播子,满足类似于qc(r, z, s)的方程(5),区别是在0 < s < 1,外场ω(r, z, s)=ωA(r, z, s)。
由于该场论模型中哈密顿量的复杂性,采用平均场近似处理,等价于使用鞍点技术求解自由能。在该近似下,通过求解
| $ \frac{\delta F}{\delta {{\phi }_{\alpha }}}=\frac{\delta F}{\delta {{\omega }_{\alpha }}}=~\frac{\delta F}{\delta \xi }=0 $ | (7) |
得出如下的平均场方程组:
| $ \begin{align} {{\phi }_{\text{A}}}\left( r,z \right)=&\int_{0}^{1}{\text{d}s{{q}_{\text{h}}}\left( r,z,s \right){{q}_{\text{h}}}\left( r,z,1-s \right)}+ \\ & {{z}_{\text{c}}}\int_{0}^{{{p}_{\text{A}}}}{\text{d}s{{q}_{\text{c}}}\left( r,z,s \right)q_{\text{c}}^{+}\left( r,z,s \right)}, \\ {{\phi }_{\text{B}}}\left( r,z \right)=&{{z}_{\text{c}}}\int_{{{p}_{\text{A}}}}^{1}{\text{d}s{{q}_{\text{c}}}\left( r,z,s \right)q_{\text{c}}^{+}\left( r,z,s \right)}, \\ {{\omega }_{\text{A}}}\left( r,z \right)=&\chi N{{\phi }_{\text{B}}}\left( r,z \right)-H\left( r,z \right)+\xi \left( r,z \right), \\ {{\omega }_{\text{B}}}\left( r,z \right)=&\chi N{{\phi }_{\text{A}}}\left( r,z \right)+H\left( r,z \right)+\xi \left( r,z \right), \\ {{\phi }_{0}}\left( r,z \right)=&{{\phi }_{\text{A}}}\left( r,z \right)+{{\phi }_{\text{B}}}\left( r,z \right). \\ \end{align} $ | (8) |
通过迭代方法解出该方程组。将解得的结果代入方程(4)中,得到体系在平均场近似下的自由能F。
2 结果与讨论让胶束从体相(4
1) 中性表面——坚硬表面
设平板H=0,则平板是中性表面,并不吸附任何组分,是一个硬平面。研究在胶束接近衬底表面过程中体系的自由能变化。将4

|
Download:
|
| 图 3 中性表面的排空效应 Fig. 3 Depletion effect of the neutral surface | |
势阱的产生是由于均聚物高分子A的平动熵引发的排空效应,分析如下:1)从图 3(a)插图的浓度图中可以看出,胶束在势阱处和在体相处时的形貌都是球形,并没有发生形变,所以体系自由能的变化并非来自形变;2)如图 3(b),胶束中心距离平面2
2) 选择性表面——软膜表面
当平板带上选择性吸附相互作用后,衬底附近的界面结构就发生了改变,从硬表面变成软膜表面。改变平板的选择性H,当H < 0代表平板吸附B组分,排斥A组分,H>0则代表吸附A组分,排斥B组分,且H的绝对值越大吸附(或排斥)作用越强。如图 4,其中ϕAP、ϕAC、ϕBC分别代表均聚物A、二嵌段共聚物的A嵌段、B嵌段的浓度分布。当H=-6时,平板强烈吸附B组分,此时AB二嵌段共聚物在平板上密集排列形成一层高分子刷层(图 4(a)),而当H=6的时候,平板强烈吸附A组分,在平板上就密集排列一层均聚物A分子层(图 4(b))。由AB嵌段共聚物构成的高分子刷层的结构和由均聚物A构成的高分子层结构虽然都是以组分A作为表面与溶液相接触,但是它们的结构和对排空效应的调控有着很大的差异。嵌段共聚物吸附在选择性表面上(H < 0)时,衬底吸附的B嵌段形成较薄的膜层,而衬底表面不吸附的A嵌段向本体伸展形成高分子刷。相反,衬底选择性吸附均聚物A(H>0)时,整个均聚物A吸附于衬底表面成非常薄的膜层。这种由表面性质变化带来的衬底附近高分子链的分布情况的改变将导致排空效应的变化。

|
Download:
|
| 图 4 选择性平板附近软膜层结构 Fig. 4 Soft membrane structure near the selective surface | |
在H < 0时,平面上形成一层AB高分子刷层,球状胶束靠近衬底时,当胶束和高分子刷表面距离接近均聚物A的Rg大小时发生排空效应,这使得排空位置变远Δz增大,而软球胶束在软平面上的排空效应也非常弱,势阱Δf非常小。
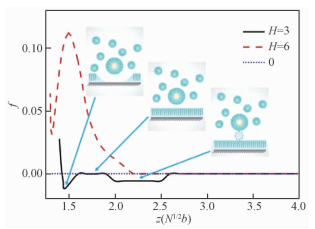
当H>0时,平板表面结构由硬平面变成软膜层平面,此时相应的排空效应也发生改变。例如H=3时,平面吸附着一层A分子软膜层(图 5)。当胶束从体相中逐渐接近平面时,先是排空自由的均聚物A高分子链团,自由能曲线上产生第1个势阱;紧接着胶束挤压到A分子软膜层引起自由能的升高;再之后AB胶束又将吸附在平板上A分子软膜层排空,自由能曲线出现第2个势阱。当平板对A组分的吸引更强,例如H=6时,其自由能曲线中,排空A链团的势阱变得不明显,只有排空A分子膜层的势阱。
|
Download:
|
| 图 5 AB胶束靠近有A软膜层的表面的自由能曲线 Fig. 5 Free energy curve of AB micelle approaching the A-homopolymer soft membrane | |
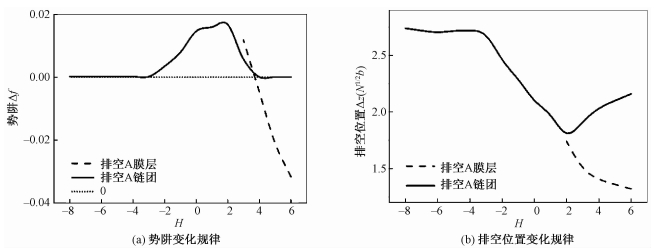
图 6给出表面选择性吸引相互作用对排空效应的调控作用。可以看出由于衬底吸引所形成的软膜层将降低排空相互作用的强度。在H < 0时,平板上形成AB高分子刷层,分子刷上方的A链团排空效应非常微弱,Δf≈0。同时,因为有分子刷的存在,Δz不再仅取决于均聚物的Rg,同时还受到高分子膜层厚度的影响。随着H→0,平板趋向于中性,不吸附分子,变成光滑硬平板,自由的A链团排空效应渐渐明显,势阱Δf渐渐增大,而因为AB软膜层的消失,Δz渐渐减小。当H>0并继续增大后,平板开始吸附A分子,平板表面上有一层A软膜层,此时A链团排空效应又变得渐渐微弱,Δf很小;因为有软膜层的存在,Δz变大。在球状胶束靠近衬底的过程中先排空自由的均聚物A链团后,随着距离的减低又继续排空吸附在衬底表面的A软膜层,H越大,软膜层越致密,厚度越薄,则排空位置越靠近平板,Δz越小;而H越大,排空软膜层耗能越高,Δf渐渐为负。
|
Download:
|
| 图 6 表面相互作用对排空效应的调整 Fig. 6 Effects of surface interaction on the depletion | |
采用自洽场方法,本文对平面衬底附近含有球状胶束和均聚物A的胶体体系进行理论计算。发现衬底表面吸附的选择性可以连续调控球状胶束和衬底间的排空相互作用。当AB胶束逐渐靠近硬平板时,通过自由能曲线的变化,观察到AB胶束对于A链团的排空作用。进一步,通过调节平板的选择性,在平板上构造A软膜层和AB高分子刷软膜层。观察到,当衬底上有软膜层出现后,胶束排空效应的势能减小,排空位置变远。本文关于软胶球与软平面间排空作用的结果对于进一步探讨胶体-高分子复合体系的相行为具有借鉴意义。
| [1] |
Oosawa F, Asakura S. Surface tension of high-polymer solutions[J]. J Chem Phys, 1954, 22(7):1255.
|
| [2] |
Li W H, Ma H R. Entropic interactions on a colloidal sphere near the edge of a terrace[J]. Eur Phys J E, 2003, 12(2):321–324.
DOI:10.1140/epje/i2003-10064-0 |
| [3] |
Li W H, Ma H R. Depletion force and torque on an ellipsoid[J]. J Chem Phys, 2003, 119(1):585–589.
DOI:10.1063/1.1577323 |
| [4] |
Li W H, Yang T, Ma H R. Depletion potentials in colloidal mixtures of hard spheres and rods[J]. J Chem Phys, 2008, 128(4):044910.
DOI:10.1063/1.2820785 |
| [5] |
Miao H, Li Y, Ma H R. Depletion interaction between two ellipsoids[J]. J Chem Phys, 2014, 140(15):154904.
DOI:10.1063/1.4870520 |
| [6] |
Li W H, Ma H R. Depletion potential near curved surfaces[J]. Phys Rev E, 2002, 66(6 Pt 1):061407.
|
| [7] |
Glandt E D. Density distribution of hard-spherical molecules inside small pores of various shapes[J]. J Colloid Interf Sci, 1980, 77(2):512–524.
DOI:10.1016/0021-9797(80)90324-0 |
| [8] |
Mao Y, Cates M E, Lekkerkerker H N W. Depletion force in colloidal systems[J]. Physica A, 1995, 222(1-4):10–24.
DOI:10.1016/0378-4371(95)00206-5 |
| [9] |
Walz J Y, Sharma A. Effect of long range interactions on the depletion force between colloidal particles[J]. J Colloid Interf Sci, 1994, 168(2):485–496.
DOI:10.1006/jcis.1994.1446 |
| [10] |
Biben T, Bladon P, Frenkel D. Depletion effects in binary hard-sphere fluids[J]. J Phys Condensed Mat, 1996, 8(50):10799–10821.
DOI:10.1088/0953-8984/8/50/008 |
| [11] |
Asakura S, Oosawa F. Interaction between particles suspended in solutions of macromolecules[J]. J Polym Sci, 1958, 33(126):183–192.
DOI:10.1002/pol.1958.1203312618 |
| [12] |
Mao Y, Cates M E, Lekkerkerker H N W. Depletion stabilization by semidilute rods[J]. Phys Rev Lett, 1995, 75(24):4548–4551.
DOI:10.1103/PhysRevLett.75.4548 |
| [13] |
Mao Y, Cates M E, Lekkerkerker H N W. Theory of the depletion force due to rodlike polymers[J]. J Chem Phys, 1997, 106(9):3721–3729.
DOI:10.1063/1.473424 |
| [14] |
Mao Y, Bladon P, Lekkerkerker H N W, et al. Density profiles and thermodynamics of rod-like particles between parallel walls[J]. Molec Phys, 1997, 92(1):151–159.
DOI:10.1080/002689797170716 |
| [15] |
Piech M, Walz J Y. Depletion interactions produced by nonadsorbing charged and uncharged spheroids[J]. J Colloid Interf Sci, 2000, 232(1):86–101.
DOI:10.1006/jcis.2000.7194 |
| [16] |
Oversteegen S M, Lekkerkerker H N W. On the accuracy of the Derjaguin approximation for depletion potentials[J]. Physica A, 2004, 341(1):23–39.
|
| [17] |
Henderson J R. Depletion interactions in colloidal fluids:statistical mechanics of Derjaguin's analysis[J]. Physica A, 2002, 313(3/4):321–335.
|
| [18] |
Lekkerkerker H N W, Tuinier R. Colloids and the depletion interaction[M]//Lecture Notes in Physics, Springer Netherlands, 2011.
|
 2018, Vol. 35
2018, Vol. 35 


