随着现代信息技术以及微加工技术的发展,以晶体管为基本工作单元的传统微电子器件已经不能满足人们对器件越来越小,存储密度越来越大的要求了。自旋电子学利用电子的自旋作为信息载体,通过操纵电子的自旋,设计出新型的电子器件,在提高信息存储密度的同时也提高信息的传输速率[1-2]。1998年,法国的Fert小组和德国的Grünberg小组[3]分别在Fe/Gr/Fe的三明治结构中发现巨磁电阻效应(giant magnetoresistance effect, GMR),即:在磁性多层膜结构中,自旋极化电流自旋方向和铁磁层磁化方向相反时电子受到的散射大,电阻大;自旋方向和铁磁层磁化方向相同时受到的散射小,电阻小。随后很多实验组在不同的三明治结构中都发现巨磁电阻效应[4-5]。
在自旋电子学的基础上,利用分子组构电子器件也开始被广泛研究和应用[6-7]。由此,一个新的研究领域——分子自旋电子学[8-9]应运而生。由分子构成的电子器件更能满足人们对存储器件高密度、小尺寸的要求,可以用作自旋过滤器和自旋极化整流器等。Callsen等[10]计算2, 2-对环芳烷吸附在铁表面而形成的稳定化合物,发现它具有很好的自旋过滤效应。Dong等[11]在由铁磁zigzag-石墨烯-纳米带电极之间连接碳原子链所构成的器件中发现很高的自旋整流值。近年来,利用扫描隧道显微镜(STM)探测分子磁性[12-13],尤其是研究单分子磁体的自旋极化输运问题一直是一个热点[14]。
单分子磁体(single molecule magnet)是一类磁性大分子,它的能级具有双势阱结构,在低温下的弛豫时间很长,呈现出和块状磁性材料类似的性质,可以长久地保持磁性[15-16]。因此单分子磁体被认为是发展新一代体积更小、集成度更高、工作效率更好的分子电子器件、信息存储器件以及量子计算系统的基础材料之一。其中引人注目的有对包含过渡族金属元素的酞菁类分子的研究,探究它的电子结构[17],探测其隧穿磁电阻效应、近藤效应等。例如,将酞菁锰分子放在钴/铜(111)衬底上,可以发现隧穿磁电阻(tunnel magnetoresistance,TMR)比值随针尖与分子的间距不同在0~100%间变化[18];在酞菁铁分子放在金(111)衬底形成的2种不同的构型中都测得近藤共振[19]。此外,还有对包含稀土元素的单离子磁体的研究。由于稀土元素单电子数多、各向异性显著,是设计单分子磁体的理想选择。例如,把含有稀土元素镝的双层夹心的单离子磁体DyPc2放在金(111)衬底上,利用低温扫描隧道显微镜和光谱去探测单个孤立的DyPc2的微分电导,没有发现近藤共振,所得结果表明镝原子几乎对隧穿电流没有贡献,这是因为双层夹心结构使得针尖很难接近镝原子并与之发生耦合[20]。Jiang等[21]和Meng等[22]研究一系列的镧系有机金属双层夹心结构的分子(Cp*)Ln(COT),Cp*代表五甲基五环二烯,Ln代表TbⅢ, DyⅢ, HoⅢ, ErⅢ, TmⅢ, COT代表环辛四烯;(Cp*)Ln(COT)系列化合物中有3例表现为单离子磁体的特征,分别是Dy,Ho和Er的化合物。本文将主要对其中的铒单离子磁体的自旋极化输运性质进行研究。
我们之所以对铒单离子磁体进行研究,是因为其观测到的能垒(323 K)是现存记录中接近最大的,并且是可观测到的磁滞回线温度比较高的单离子磁体(5 K)。我们将铒单离子磁体分正立(upward)和倒立(downward)2种情况放置在金(111)表面,中间的铒离子正对着金原子放置。结果发现铒单离子磁体具有很强的TMR效应,并且upward和downward这2种构型都有很大的自旋过滤效率, 此外,downward构型还具有较大的整流值。
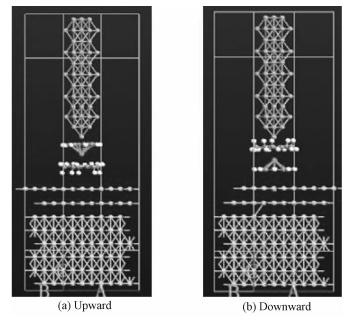
1 器件结构和计算方法研究由扫描隧道显微镜(STM)钴针尖,铒单离子磁体,金(111)衬底3部分组成的单离子磁体器件,按照单离子磁体放置在金衬底上的方式,可以分正立和倒立2种情况,如图 1所示。钴针尖最上面的4层与金(111)衬底最下面的3层原子分别作为上下电极,中间部分做为中心区,整个器件共有224个原子,其中钴原子54个,金原子128个,其余的则构成铒单离子磁体。为方便起见,下文直接用upward和downward代表这2种构型。用基于密度泛函理论的vasp软件包[23]优化这2种构型,其中采用广义梯度近似(GGA)的PBE作为交换关联泛函,同时采用投影缀加平面波(PAW)方法构造赝势。平面波动能截断选取为400 eV, K抽样使用的是Γ点,周期性的原胞包含6层金衬底,一个铒的单离子磁体和15 Å左右的真空层,原胞中最下面的4层金属原子被固定。优化判据为原子最小受力小于0.05 eV/Å。量子输运的计算采用的是基于非平衡格林函数理论的ATK14.2软件包[24-25],使用的是其中半经验的extended Hückel(EH)方法[26]。当在两端电极加上偏压Vb后,左右电极的化学势也就确定下来了,分别是μL=εLF-eVb/2和μR=εLF+eVb/2,其中εLF和εRF加是左右电极的费米能级。如果所得是正偏压,则电流会从左电极流向右电极,此时非平衡态的电流为
| $ I = \frac{e}{h}\int_{ - \infty }^{ + \infty } {T(E;{V_{\rm{b}}})[{f_{\rm{L}}}(E;{\mu _{\rm{L}}}) - {f_{\rm{R}}}(E;{\mu _{\rm{R}}})]{\rm{d}}E} , $ | (1) |
|
Download:
|
| 图 1 正立和倒立器件结构 Fig. 1 Upward and downward structure | |
式中:T(E; Vb)为电子透射谱,表示不同能量的电子透射概率,
| $ \begin{array}{l} T\left( {E;{V_{\rm{b}}}} \right) = {\rm{Tr}}[{\mathit{\widehat \Gamma }_{\rm{L}}}\left( {E;{V_{\rm{b}}}} \right)\mathit{\widehat G}{\;^\dagger }\left( {E;{V_{\rm{b}}}} \right)\\ \quad \quad {\mathit{\widehat \Gamma }_{\rm{R}}}(E;{V_{\rm{b}}})\mathit{\widehat G}(E;{V_{\rm{b}}})], \end{array} $ | (2) |
式中:
在我们的计算中,K抽样选取的是3×3×100,用于非平衡格林函数在实轴上的积分的能量网格截断是20 Hartree,体系温度为7 K,收敛精确到7e-05 Hartree。铒是稀土元素,所以自旋轨道耦合效应可能会对体系的自旋过滤有较大影响,但由于计算条件限制,本文中并没有将该效应考虑进去。
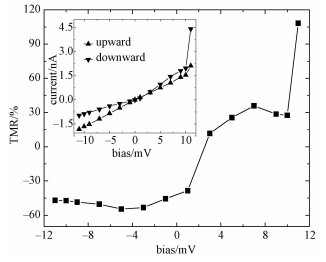
2 计算结果及分析首先计算铒单离子磁体在2种不同构型下电流随偏压的变化情况,如图 2中插图所示。Upward构型得到的I-V曲线几乎是线性的,而downward构型的I-V曲线则呈现出明显的非线性现象,在正偏压时电流比upward构型增长快,在负偏压时电流又比upward构型减小慢。由于2种构型的电流在较大偏压下差别明显,所以可以用这2种构型作为信息的载体,即0态和1态,因为它们电流差别明显,可以很方便地区分开来。为此定义体系的隧穿磁电阻(TMR)为
| $ {\rm{TMR}} = \frac{{{I_{{\rm{down}}}} - {I_{{\rm{up}}}}}}{{{I_{{\rm{up}}}}}}, $ | (3) |
|
Download:
|
| 图 2 隧穿磁电阻和电流随偏压的变化 Fig. 2 TMR and current as functions of bias | |
式中:Iup代表upward构型的电流,Idown代表downward构型的电流,结果如图 2所示。由图中可以看出TMR值随电压在-50%~120%间变化,说明铒单离子磁体是很好的磁存储材料。
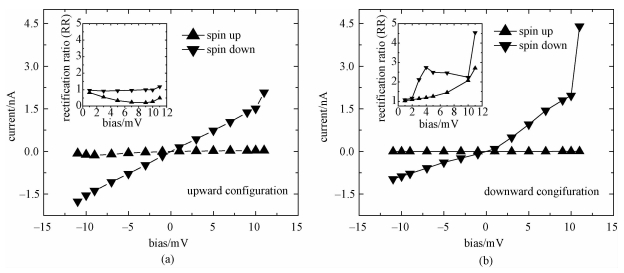
由于铒是有磁性的稀土元素,钴也是有磁性的金属元素,所以我们又研究2种结构自旋极化电流随电压的变化,如图 3所示。可以看出这2种结构电流的主要贡献都是来自自旋向下的电流,自旋向上的电流几乎为零,因而呈现出很强的自旋过滤效应。
|
Download:
|
| 图 3 极化电流和整流比随偏压的变化 Fig. 3 Polarization current and RR as functions of bias | |
为进一步展示这种强的自旋过滤效应,计算零偏压下自旋过滤效率(equilibrium spin filter efficiency,ESFE)和偏压依赖的自旋注入系数(bias dependence spin injection coefficient,BDSIC)。零偏压下的自旋过滤效率SFE[12]通过自旋向上和向下的透射谱计算得到,其定义为
| $ {\rm{SFE}} = \frac{{{T_ \uparrow }({E_{\rm{F}}}) - {T_ \downarrow }({E_{\rm{F}}})}}{{{T_ \uparrow }({E_{\rm{F}}}) + {T_ \downarrow }({E_{\rm{F}}})}} \times 100\% , $ | (4) |
式中:T↑(EF)和T↓(EF)分别表示自旋向上和自旋向下通道的透射系数。根据式(4),通过计算得到upward构型的SFE值高达82%,而downward构型的SFE值也达到79%。在计算有限偏压下的自旋过滤效率时,其公式的定义和零偏压下自旋过滤效率的定义不一样,所得结果自然会有不同。有限偏压下的BDSIC(η)[12]值时,其定义如下
| $ \eta = \frac{{{I_{{\rm{spin}}\;{\rm{down}}}} - {I_{{\rm{spin}}\;{\rm{up}}}}}}{{{I_{{\rm{spin}}\;{\rm{down}}}} + {I_{{\rm{spin}}\;{\rm{up}}}}}} \times 100\% , $ | (5) |
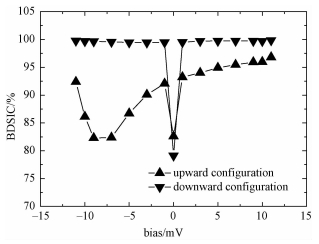
式中:Ispin up和Ispin down分别表示自旋向上和自旋向下的电流。BDSIC随偏压的变化在图 4给出,从图中可以看出,大多数偏压下的自旋过滤效率比零偏压时高,而downward构型的自旋过滤效率在有限偏压下普遍比upward构型的要高,因此downward构型是很好的自旋过滤元件。
|
Download:
|
| 图 4 自旋注入系数随偏压的变化 Fig. 4 BDSIC as function of bias | |
铒单离子磁体器件除在磁存储和自旋过滤上有重要应用外,我们预期它在自旋整流上也应该有自己的用处。为此研究2种构型的整流比(rectification ration,RR),其定义如下
| $ {\rm{RR}} = \left| {\frac{{{I_{{\rm{spin}}\;{\rm{up/down}}}}\left( V \right)}}{{{I_{{\rm{spin}}\;{\rm{up/down}}}}\left( { - V} \right)}}} \right|. $ | (6) |
根据式(6),计算出这2种构型的整流比,如图 3中插图所示。对比图 3(a)和3(b)可以看出,downward构型有比较大的整流比。由于downward构型也有相对较大的自旋过滤效率,所以铒单离子磁体尤其是downward构型有很大潜能用来构成多功能器件,如整流器件和自旋过滤器件。
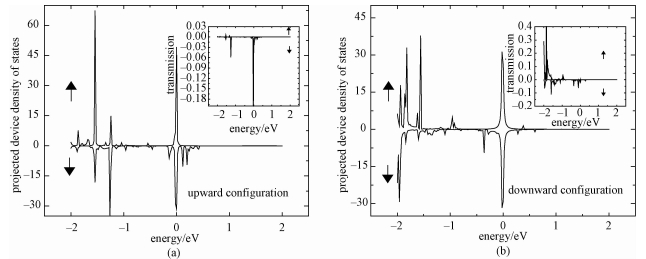
由于电流是由体系的透射谱决定的,上述与电流有关的TMR效应、自旋过滤效应以及整流效应也与透射谱有关,前面曾提到,我们计算的ESFE值是由零偏压的透射谱得到的,而且主要是由费米能级处的透射值得出的。为进一步研究这些现象,有必要对体系的透射谱进行分析,2种构型的透射谱如图 5中插图所示。由图 5(a)和5(b)可以看出在费米能级处自旋向上的透射值几乎为零,主要贡献来自自旋向下的透射值,这与前面得到的2种构型的自旋极化电流曲线符合。upward构型费米能级处的透射值比downward构型的值要大,所以upward构型的ESFE值也要大些。对于有限偏压下的透射谱,其主要贡献来自于两电极化学势之间的能量范围。由于所加偏压比较小,所以能量范围还是集中在费米能级附近,其透射谱与零偏压类似。由于篇幅所限相应的图并未在文中给出,但可以看出,对电流的贡献仍主要来自自旋向下的通道,并且downward构型的透射谱在费米能级附近的透射值明显比upward构型的大。所以downward构型的电流值就比upward的电流值大,这与图 2得到的结果相符。如图 5(a)所示,对于零偏压下upward构型的透射谱,自旋向下的透射通道在-1.54、-1.26、-0.02 eV附近有很窄的尖锋。downward构型(如5(b)所示)在-1.96、-1.6、-0.36和-0.1 eV附近有尖锋存在。因为体系的透射谱与态密度有关,所以又进一步研究体系的态密度。图 5是2种构型零偏压下整个体系投影到铒单离子磁体的器件态密度图(PDDOS)。对比图 5(a)、5(b),发现2种构型的透射谱和PDDOS有相似的能量峰值,表明铒单离子磁体的透射谱和态密度是一致的。
|
Download:
|
| 图 5 零偏压下透射谱和投影器件态密度 Fig. 5 Transmission and PDDOS at zero bias | |
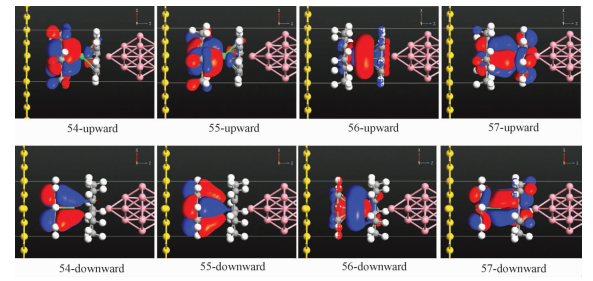
为了更好地理解电子在铒单离子磁体器件中的电荷转移特性,计算体系的MPSH(molecular projected self-consistent Hamiltonian)态。MPSH态是由整个体系自洽哈密顿量的分子部分对角化得到。图 6为2种构型对于自旋向下的电子的MPSH态54-57。计算分子能谱可知MPSH态55即为HOMO, MPSH态56即LUMO。由图 5(a)、图 5(b)看出自旋向下的透射通道在金电极费米能级附近有峰值,当铒单离子磁体与金电极发生耦合之后,54、55这2个轨道就都被占据了,说明有电荷从衬底表面转移到LUMO轨道。
|
Download:
|
| 图 6 自旋向下的分子投影自洽哈密顿态 Fig. 6 Spin-down MPSH states | |
为进一步研究此透射本征态,计算在峰值处自旋向下通道的透射本征值,选取最大本征值对应的透射本征态,可以看出Upward构型在-0.02 eV的透射本征态与MPSH态54,即HOMO-1非常相似,说明我们的计算是正确的。
3 小结搭建一种单分子磁体器件,该器件是由金衬底(111)、铒单离子磁体、钴针尖3部分构成,可以形成铒单离子磁体正立和倒立2种构型。运用非平衡格林函数理论,在半经验的extended Hückel(EH)模型下计算这2种构型的I-V曲线,发现体系的TMR值最高可达120%,所以铒单离子磁体是很好的磁存储材料。通过计算体系的自旋极化电流,发现这2种构型的电流几乎都是由自旋向下的电子贡献,这与进一步计算的零偏压和有限偏压下的透射谱、PDDOS、MPSH态以及透射本征态的结果是一致的。通过计算体系的BDSIC和RR系数,发现2种构型都有很强的自旋过滤效应,且downward构型比upward构型有较大的自旋整流值,所以downward构型可以作为自旋过滤器和自旋极化整流器,是一种多功能的分子器件。
| [1] |
Wolf S A, Awschalom D D, Buhrman R A, et al. Spintronics:a spin-based electronics vision for the future[J]. Science, 2001, 294(5546):1488–1495.
DOI:10.1126/science.1065389 |
| [2] |
Zutic I, Fabian J, Sarma S D. Spintronics:fundamentals and applications[J]. Reviews of Modern Physics, 2004, 76(2):323–410.
DOI:10.1103/RevModPhys.76.323 |
| [3] |
Baibich M N, Broto J M, Fert A, et al. Giant magnetoresistance of (001)Fe/(001) Cr magnetic superlattices[J]. Physical Review Letters, 1988, 61(21):2472–2475.
DOI:10.1103/PhysRevLett.61.2472 |
| [4] |
Butler W H, Zhang X G, Schulthess T C. Spin-dependent tunneling conductance of Fe|MgO|Fe sandwiches[J]. Physical Review B, 2001, 63(5):054416.
DOI:10.1103/PhysRevB.63.054416 |
| [5] |
Yang Z, Wang D H, Liu X G, et al. Magnetic and quantum transport properties of small-sized transition-metal-pentalene sandwich cluster[J]. The Journal of Physical Chemistry C, 2014, 118(51):29695–29703.
DOI:10.1021/jp511443j |
| [6] |
Heurich J, Cuevas J C, Wenzel W, et al. Electrical transport through single-molecule junctions:from molecular orbitals to conduction channels[J]. Physical Review Letters, 2002, 88(25):256803.
DOI:10.1103/PhysRevLett.88.256803 |
| [7] |
Heersche H B, Groot Z D, Folk J A, et al. Electron transport through single Mn12 molecular magnets[J]. Physical Review Letters, 2006, 96(20):206801.
DOI:10.1103/PhysRevLett.96.206801 |
| [8] |
Bogani L, Wernsdorfer W. Molecular spintronics using single-molecule magnets[J]. Nature Materials, 2008, 7:179–186.
DOI:10.1038/nmat2133 |
| [9] |
Emberly E G, George K. Molecular spintronics:spin-dependent electron transport in molecular wires[J]. Chemical Physics, 2002, 281(2/3):311–324.
|
| [10] |
Callsen M, Caciuc V, Kiselev N, et al. Magnetic hardening induced by nonmagnetic organic molecules[J]. Physical Review Letters, 2013, 111(10):106805.
DOI:10.1103/PhysRevLett.111.106805 |
| [11] |
Dong Y J, Wang X F, Yang S W, et al. High performance current and spin diode of atomic carbon chain between transversely symmetric ribbon electrodes[J]. Scientific Reports, 2014, 4:6157.
|
| [12] |
Cheng Z H, Du S X, Jiang N, et al. High resolution scanning-tunneling-microscopy imaging of individual molecular orbitals by eliminating the effect of surface charge[J]. Surface Science, 2011, 605(3/4):415–418.
|
| [13] |
Repp J, Meyer G. Molecules on insulating films:scanning-tunneling microscopy imaging of individual molecular orbitals[J]. Physical Review Letters, 2005, 94(2):026803.
DOI:10.1103/PhysRevLett.94.026803 |
| [14] |
Wang Y F, Wu K, Jörg K, et al. Review article:structures of phthalocyanine molecules on surfaces studied by STM[J]. AIP Advances, 2012, 2(4):041402.
DOI:10.1063/1.4773458 |
| [15] |
Sessoli R, Gatteschi D, Caneschi A, et al. Magnetic bistability in a metal-ion cluster[J]. Nature, 1993, 356:141–143.
|
| [16] |
Gatteschi D, Caneschi A, Pardi L, et al. Large clusters of metal ions:the transition from molecular to bulk magnets[J]. Science, 1994, 265(5175):1054.
DOI:10.1126/science.265.5175.1054 |
| [17] |
Liao M S, Steve S. Electronic structure and bonding in metal phthalocyanines, Metal=Fe, Co, Ni, Cu, Zn, Mg[J]. Chemical Physics, 2001, 114(22):9780–9791.
|
| [18] |
Hsu C H, Chu Y H, Lu C, et al. Spin-polarized transport through single manganese phthalocyanine molecules on a Co nanoisland[J]. Journal of Physical Chemistry C, 2015, 119:3374–3378.
DOI:10.1021/jp510930y |
| [19] |
Gao L, Ji W, Hu Y B, et al. Site-specific kondo effect at ambient temperatures in iron-based molecules[J]. Physical Review Letters, 2007, 99(10):106402.
DOI:10.1103/PhysRevLett.99.106402 |
| [20] |
Zhang Y, Liao P, Kan J, et al. Low-temperature scanning tunneling microscopy study on the electronic properties of a double-decker DyPc2 molecule at the surface[J]. Physical Chemistry Chemical Physics, 2015, 17(40):27019–27026.
DOI:10.1039/C5CP03925H |
| [21] |
Jiang S D, Liu S S, Zhou L N, et al. Series of lanthanide organometallic single-ion magnets[J]. Inorganic Chemistry, 2012, 51(5):3079–3087.
DOI:10.1021/ic202511n |
| [22] |
Meng Y S, Wang C H, Zhang Y Q, et al. (Boratabenzene)(cyclooctatetraenyl) lanthanide complexes:a new type of organometallic single-ion magnet[J]. Inorganic Chemistry, 2016, 3(6):828–835.
|
| [23] |
Kresse G, Furthmuller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Physical Review B, 1996, 54(16):11169–11186.
DOI:10.1103/PhysRevB.54.11169 |
| [24] |
Brandbyge M, Mozos J L, Ordejón P, et al. Density-functional method for nonequilibrium electron transport[J]. Physical Review B, 2002, 65(16):165401.
DOI:10.1103/PhysRevB.65.165401 |
| [25] |
Stokbro K, Petersen D E, Smidstrup S, et al. Semiempirical model for nanoscale device simulations[J]. Physical Review B, 2010, 82(7):075420.
DOI:10.1103/PhysRevB.82.075420 |
| [26] |
Stokbro K, Taylor J, Brandbyge M, et al. Theoretical study of the nonlinear conductance of Di-thiol benzene coupled to Au(111) surfaces via thiol and thiolate bonds[J]. Computational Materials Science, 2003, 27(1/2):151–160.
|
 2018, Vol. 35
2018, Vol. 35 


