自从石墨烯从块体石墨中成功分离以来，二维材料引起众多研究人员的兴趣^[1]。由于制备技术的进步，二维层状材料家族也得到很大的拓展，诸如黑磷、硅烯、二硫化钼、锡烯和一氧化锡等二维材料相继被成功制备^[2-6]。在一系列二维材料中发现许多新奇物性，极大地丰富了人们对二维材料的认识^[7-11]。研究发现，单层一氧化锡是典型的P型半导体，其场效应迁移率在0.05~1.9 cm²·V^-1·s^-1之间，对互补金属氧化物半导体场效应管(CMOS)的发展，具有重要推动作用；单层二硫化钼是具有1.90 eV直接带隙的半导体，特别适合应用于纳米电子学和谷电子学之中。最近发现，二维拓扑绝缘体可以极大地增加热电转换效率，促进了热电器件设计和应用的发展。在二维过渡金属卤族化合物中，如一氯化锆、一溴化锆和一氯化铪等，研究发现其能带具有0.12~0.4 eV带隙，并具有量子自旋霍尔效应，这类材料在实现无能耗电子器件中可能有重要应用前景^[12-13]。有研究报道，二维三氯化钒、碘化钒、三氯化钛和二氯化铁是半金属材料^[14-16]。在对过渡金属卤族化合物块体研究中，也发现很多重要的物理性质。在二氯化铜和二溴化铜块体中，发现磁振荡效应，该效应可以通过外加电场调节磁化状态，反之亦然，因此可以用于探测技术中^[17-18]。由于二维材料和过渡金属卤族化合物的重要性，促使我们去发现更多具有新奇性质的二维过渡金属卤族化合物。

半金属是金属材料中的一种特殊类型。在半金属材料中，在费米面只存在一种自旋极化方向的导电电子，另一种自旋方向的电子表现出半导体或绝缘体性质^[19]。半金属性质在自旋电子学中有重要应用^[20]。之前关于半金属块体材料的研究主要集中于Heusler合金和CrO₂等材料，在二维材料中，主要通过磁性掺杂、制造缺陷、化学修饰和电场调控等方式实现半金属性质^[21-23]，在已经被制备的二维材料中，内禀半金属性的报道尚不多见。在本文中，设计提出的单层三氯化锆具有内禀半金属性质，丰富了自旋电子学器件的材料体系。

本文中所有的第一性原理计算均基于VASP程序包来实现^[24-25]。基于密度泛函(DFT)理论的VASP程序被认为是目前最可靠的计算程序之一^[26]。在计算过程中，采用投影缀加平面波(PAW)方法构造的赝势^[27]。在自旋极化计算中，采用具有广义梯度近似(GGA)的PBE作为交换关联泛函^[28]。为避免层与层之间的相互作用，选取大于15 Å的真空层。为尽量提高计算精度，采用Monkhorst-Pack方法^[29]以19×19×1的密度在第一布里渊区进行采样，选取700 eV的平面波动能截断。对三氯化锆原胞进行充分的结构优化，赫尔曼-费曼力(H-F force)收敛标准设定为0.001 eV/Å，能量收敛标准设为10^-5 eV。声子谱的计算是结合VASP和PHONOPY程序实现的。首先用VASP程序计算出二阶力常数，然后将力常数作为PHONOPY程序的输入参数，最后得到声子谱。由于二阶力常数需要使用比较大的超胞，经过反复测试，计算二阶力常数时采用5×5×1的超级原胞，每个超级原胞中包含200个原子。考虑到过渡金属的强关联效应对电子结构的影响，使用LDA+U方法进行计算，U值取为5 eV。另外使用Bader程序计算离子之间的电荷转移^[30]。

三氯化锆每个原胞中有8个原子，中间一层金属锆原子被上下两层氯原子包裹起来，形成类似三明治的几何结构，两层氯原子之间的距离计算结果为3.62 Å。每个金属锆原子周围有6个氯原子，氯原子与锆原子之间的距离为2.55 Å，这些氯原子与锆原子之间有两类键角(α，β)，α为92.13°，β为90.25°。所有金属锆原子构成六角格子，几何结构如图 1(a)所示。充分优化结构，得到的晶格常数为6.25 Å。计算出的所有结构参数列在表 1中。声子谱是晶格振动频率和波矢的色散关系，若声子谱中没有虚频，说明晶格在平衡位置附近做简谐振动，不会偏离平衡位置很远，因此，声子谱中没有虚频被认为结构是动力学稳定的重要判据。图 1(b)展示单层三氯化锆的声子谱，可以看出声子谱没有虚频，说明该结构是动力学稳定的。

Fig. 1

	Download: JPG larger image
图 1 单层三氯化锆几何结构和声子谱 Fig. 1 Structure and phonon spectra of zirconium trichloride monolayer

Table 1

表 1 单层三氯化锆物理参数 Table 1 Physical parameters of zirconium trichloride monolayer a/Å dCl-Cl/Å dZr-Cl/Å α/(°) β/(°) μ/μB ΔρZr/e ΔρCl/e AFM/eV FM/eV Eex/meV ZrCl3 6.25 3.62 2.55 92.13 90.25 2 1.99 0.66 -41.321 -41.685 364

表 1 单层三氯化锆物理参数 Table 1 Physical parameters of zirconium trichloride monolayer

用Z_c^*和Z_a^*分别表示阳离子和阴离子的有效电荷，定义Δρ=Z_a^*-Z_v为从阳离子转移到一个阴离子的电荷量，Δρ=Z_c^*-Z_v为从一个阳离子转移到阴离子的电荷量，其中Z_v表示对应原子的化合价。从表 1可以看出，每个锆原子转移1.99电荷给3个氯原子，这说明三氯化锆是靠较强的离子键结合而成的。

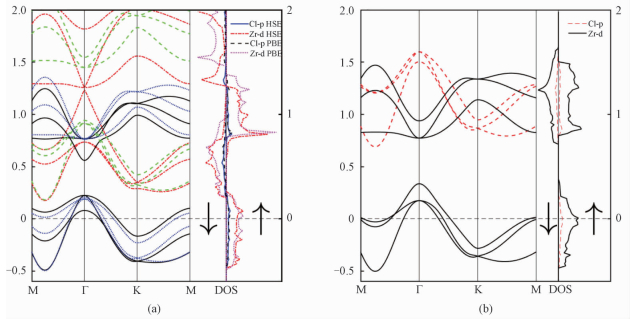
通过计算单层三氯化锆的能带和分波态密度，发现它是半金属材料，如图 2所示，黑色实线和红色点画线表示HSE修正后的能带，蓝色点线和绿色虚线表示PBE计算结果。把自旋方向和原子磁矩方向一致的电子所处的状态定义为多数态，而自旋方向相反的电子所处的态定义为少数态，在能带图中，黑色实线和蓝色点线表示多数态，红色点画线和绿色虚线表示少数态。由于三氯化锆的少数态能级处于费米能量以下，而多数态能级和费米面相交，说明三氯化锆具有半金属性质。能带计算表明，处于少数态的电子有一个3.8 eV的带隙，处于少数态的电子具有良好的热稳定性。通过HSE计算，发现三氯化锆仍然是半金属，少数态能隙变为3.6 eV，如图 2(a)所示。从分波态密度可以看出，锆原子的d电子对半金属态贡献最大。从态密度中可以观察到，当给三氯化锆加门电压时，可以得到以另一自旋极化方向的电子作为传导电子的导体。因此，不加门电压时自旋向上的电子导通，而加门电压时自旋向下的电子导通。该性质在自旋阀器件中会有重要应用。

Fig. 2

	Download: JPG larger image
费米能量位于零处。 图 2 单层三氯化锆能带和态密度 Fig. 2 Band structure and density of states of zirconium trichloride monolayer (Fermi energy equals zero)

我们注意到有文献报道了具有类似结构的多层α-RuCl₃在实验室中被剥离出来^[31].作为对比，计算单层α-RuCl₃能带结构和态密度，显示该材料具有半金属性。在块体α-RuCl₃材料中，文献[32]采用U=1.5 eV进行能带结构计算，因为单层材料强关联效应比块体更强，采用LDA+U重新计算其能带和态密度，发现当U=5 eV时，该材料由半金属变为一个绝缘体，在单层FeCl₂中^[16]，也发现U=5 eV时，该体系从半金属转变为绝缘体。类似地，使用LDA+U的方法重新计算三氯化锆的能带和态密度，其中取U=5 eV，发现三氯化锆依然保持半金属性不变，如图 2(b)所示，由此认为单层三氯化锆是一个稳定的半金属材料，这对自旋电子学将有重要意义.

为探究三氯化锆铁磁态的稳定性，计算铁磁态和反铁磁态的能量，其结果列于表 1，可以看出反铁磁态能量比铁磁态能量高364 meV。因此，从能量角度看，三氯化锆的铁磁态比反铁磁态更稳定。

借助基于二维伊辛模型的蒙特卡洛模拟估算单层三氯化锆的居里温度^{[15, 33]}。在经典海森堡模型中，二维格子的哈密顿量可以表示为H=-J∑_ijμ_iμ_j，其中J代表海森堡交换常数，可以由 $J = \frac{1}{6}\frac{{{E_{{\rm{ex}}}}}}{{2{\mu ^2}}}$ 计算，其中E_ex表示铁磁态和反铁磁态的能量差，1/6表示重复计算锆原子和最近邻3个锆原子的相互作用，μ表示每个原胞的磁矩。将E_ex=364 meV和μ=2μ_B代入J的公式，可以计算出J=7.58 meV。在蒙特卡洛模拟中，把每个锆原子看作一个格点，每个格点可以有自旋向上和自旋向下两种状态，所有锆原子所在的格点组成一个六角格子。模拟中使用Wolff方法^[34]，使用70×70的超胞以减小周期的影响。在每个温度下，循环步数设定为1×10⁹。从图 3可以看出单位元胞的磁矩在温度大约为130 K时急剧下降到接近零，显示出三氯化锆的居里温度大约是130 K。

Fig. 3

	Download: JPG larger image
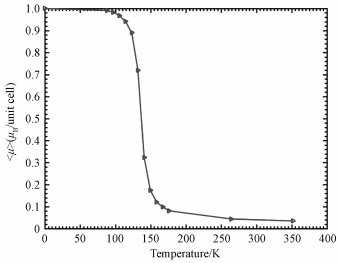
图 3 伊辛模型近似下的二维单层三氯化锆的相变曲线 Fig. 3 Phase transition of zirconium trichloride monolayer

通过第一性原理计算，系统研究单层三氯化锆的几何结构、电子结构和磁性质，发现该材料是动力学稳定的，并且是一个理想的半金属材料，其单位原胞磁矩为2μ_B，铁磁态比反铁磁态更稳定。从能带结构可以看出，该材料的少数态能隙为3.8 eV，说明它受温度干扰较小。通过蒙特卡洛模拟，计算出该材料的居里温度约为130 K。通过LDA+U计算，验证了该材料中强关联效应不显著，半金属性质仍然得以保留。本研究将在自旋电子学器件的发展中具有潜在的应用价值。