近年来,随着海洋事业的发展,新型舰船动力系统在船舶推进、海水淡化和海洋供电等领域引起了广泛关注。例如,海洋核平台可以运行于沿海区域,为岛屿和采油平台等提供电力和淡水。与陆地核动力系统相比,海洋核动力系统具有造价低、建造周期短、移动方便等特点,并且在抗震和退役处理技术方面也具有明显优势。随着第4代核能技术的发展,超临界流体在核动力系统中的应用逐渐增加,由于超临界动力转换系统与高温反应堆具有良好的匹配性,循环效率远高于常规朗肯循环,因此在海洋事业中具有极大的应用前景。
由于海洋环境下存在风和浪的作用,船体会出现起伏、摇摆等跟随运动,超临界动力系统在摇摆条件下受到周期性变化的离心力、切向力、重力、科式力及浮升力等体积力的协同作用,导致超临界流体流动和传热特性发生显著变化。随着实验与数值技术的不断改进,国内外学者陆续开展了对海洋条件下流体传热问题的相关研究。
Pendyala等[1]对起伏条件下单相水的强迫对流传热特性进行实验研究,研究表明重力场导致层流区流量出现显著脉动,进而增强传热。贾辉等[2]通过对比静止和摇摆条件下单相水的对流传热特性,发现摇摆运动引起的流量脉动增加了流道换热系数,且换热系数随摇摆振幅及摇摆频率增加而增加。但是近期研究表明,摇摆条件下单相强迫循环流量脉动与否很大程度上依赖于驱动压头的大小。
谭思超等[3]通过试验研究摇摆运动下单相水自然循环不稳定性和传热特性,通过对摇摆条件下的流体进行受力分析,充分考虑附加惯性力对流动的影响,研究认为,摇摆有利于自然循环传热系数的提高,摇摆运动越剧烈,换热系数提高越多。但是,Yan和Yu[4]研究摇摆运动下的自然循环特性却发现,当摇摆幅值较小时,有利于增强换热,然而,幅值较大即摇摆较剧烈时,将削弱系统的换热效果。Chang与Huang[5]针对纵摇与横摇对板式换热器、锯齿状扭带内置通道内的传热特性影响进行实验研究,结果同样表明,摇摆既可能强化通道内的换热特性,也有可能导致换热性能减弱。林玮等[6]综合前人研究后发现,海洋摇摆条件会对流动与换热造成影响,而传热的强化或削弱依具体海况而不同。
综上所述,现有研究主要是通过实验与数值分析的方法研究单相水在海洋条件下传热和阻力的变化规律,对于现役压水堆和蒸汽朗肯循环具有重要的指导意义。不同于单相水,超临界流体在升温过程中密度会发生剧烈变化,这既产生了复杂的浮升力作用,又加剧了摇摆附加力的影响。由于以上多种作用力的综合影响,摇摆条件下超临界流体的传热流动特性相对更加难以预测,因此现有研究成果无法推广到超临界流体。本文对海洋摇摆条件下超临界流体的传热特性进行研究,利用数值模拟方法对超临界流体传热流动特性的影响机理进行分析。
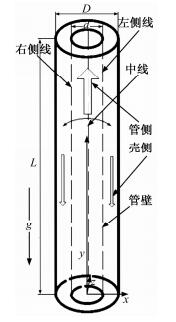
1 物理模型本研究采用的换热元件为套管式换热器,该换热器由2根同心圆管组成,管侧和壳侧的流体流向相反,换热器立式放置,管侧工质为跨拟临界区的超临界压力CO2,壳侧工质为高温超临界CO2。中心管的内径di=5.0 mm,外管(壳侧)内径为10 mm。该换热器的耦合传热段长度为L/di=200,运行压力选为7.58 MPa。高温超临界CO2在壳侧流动,热量通过管壁传递给管内的拟临界区CO2。本研究的基准工况为管侧质量流速300 kg·m-2·s-1,管侧入口温度300 K,管侧入口Re=2.4×104,壳侧质量流速200 kg·m-2·s-1,壳侧入口温度573 K,壳侧入口Re=3.6×104,管侧和壳侧流动都处于完全湍流区。摇摆轴心位于管侧入口横截面的圆心处,图 1给出管侧壁面最具代表性的3个位置的母线,即右侧线、中线和左侧线,通过研究这3条母线壁面的传热系数和壁温分布,进而研究超临界流体传热过程中物性变化、重力和离心力、科氏力等对管侧超临界流体传热特性的耦合作用机理。
|
Download:
|
| 此为上升流, 当下降流时g方向相反。 图 1 套管式换热器示意图 Fig. 1 Schematic of the double-pipe heat exchanger | |
由于舰船的摇摆周期通常大于2 s[7],因此本研究以摇摆周期2 s,摇摆幅值20°作为基准摇摆条件。近年来,很多学者[8-10]都发现,当驱动压头较低时,管路内的流量会由于摇摆条件产生周期性波动,但是当驱动压头较高时,海洋摇摆条件几乎对系统流量不会产生影响。由于超临界二氧化碳能量转换系统的驱动压头远远大于海洋摇摆条件产生的附加阻力[11-12],因此其系统流量波动可以忽略不计。
2 数学模型 2.1 控制方程和湍流模型在海洋条件瞬变外力场下,流体随体坐标系为非惯性坐标系,受到附加力的影响,流体守恒方程发生一定的变化,需要对其进行修正。守恒方程包括质量守恒方程、动量守恒方程和能量守恒方程。
海洋条件下流体的质量守恒方程与稳态条件下的方程相同。
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0. $ | (1) |
在海洋条件下,流场分布与流体运动特性受到随时间和空间变化的附加力的影响,因而需要对动量方程进行修改,时均形式的动量方程可以表示为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}{u_j}} \right) = \\ - \frac{{\partial {\rm{p}}}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right] + \\ \frac{\partial }{{\partial {x_j}}}\left( { - \rho {{u'}_i}{{u'}_j}} \right) + \rho g + Fa, \end{array} $ | (2) |
式中,Fa为摇摆运动引起的附加力,可以表示为
| $ Fa = \rho \mathit{\boldsymbol{\alpha }} = \rho \left[ {\mathit{\boldsymbol{\beta }} \times r + \mathit{\boldsymbol{\omega }} \times \left( {\mathit{\boldsymbol{\omega }} \times r} \right) + 2\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{u}}} \right], $ | (3) |
其中,ω和β分别表示摇摆角速度和角加速度,r为摇摆半径。
| $ \mathit{\boldsymbol{\omega }} = - \frac{{2{\rm{ \mathsf{ π} }}{\theta _{\rm{m}}}}}{T}\sin \frac{{2{\rm{ \mathsf{ π} }}t}}{T}, $ | (4) |
| $ \mathit{\boldsymbol{\beta }} = - \frac{{4{{\rm{ \mathsf{ π} }}^2}{\theta _{\rm{m}}}}}{{{T^2}}}\cos \frac{{2{\rm{ \mathsf{ π} }}t}}{T}. $ | (5) |
其中,θm和T分别为摇摆振幅和摇摆周期。通过修改源项中对应的数值可以改变摇摆振幅和周期,进而分析不同摇摆环境对超临界流动动量的影响。
能量守恒方程可以表示为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_i}}}\left( {{u_i}\left( {\rho E + p} \right)} \right) = \\ \frac{\partial }{{\partial {x_i}}}\left( {{\lambda _{{\rm{eff}}}}\frac{{\partial T}}{{\partial {x_i}}} - \sum\nolimits_{j'} {{h_{j'}}{J_{j'}}} + {u_j}{{\left( {{\tau _{ij}}} \right)}_{{\rm{eff}}}}} \right) \end{array} $ | (6) |
前人研究表明[13-14],AKN k-ε模型在超临界二氧化碳的传热特性预测方面具有良好的准确性,因此本研究选用AKN k-ε模型作为湍流模型。
湍动能方程
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}k} \right) = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] + }\\ {{P_k} + {G_k} - \rho \varepsilon ,} \end{array} $ | (7) |
湍动耗散方程
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}\varepsilon } \right) = \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + }\\ {{C_{\varepsilon 1}}{f_1}\frac{1}{{{T_t}}}\left( {{P_k} + {G_k}} \right) - {C_{\varepsilon 2}}{f_2}\frac{{\rho \varepsilon }}{{{T_t}}} + \rho E,} \end{array} $ | (8) |
| $ {\mu _t} = \rho {C_\mu }{v^2}{T_t} = \rho {C_\mu }{f_\mu }\frac{{{k^2}}}{\varepsilon }. $ | (9) |
式中,衰减函数fμ、f1、f2则保证低雷诺数k-ε湍流模型在近壁面区域的有效性[15]。
| $ {f_1} = 1.0, $ | (10) |
| $ \begin{array}{*{20}{c}} {{f_2} = \left\{ {1 - 0.3\exp \left[ { - {{\left( {\frac{{\mathit{R}{\mathit{e}_t}}}{{6.5}}} \right)}^2}} \right]} \right\} \cdot }\\ {{{\left[ {1 - \exp \left( { - {y^ * }/3.1} \right)} \right]}^2},} \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {{f_\mu } = \left\{ {1 + 5/\mathit{Re}_\tau ^{3/4}\exp \left[ {1 - {{\left( {\frac{{\mathit{R}{\mathit{e}_\tau }}}{{200}}} \right)}^2}} \right]} \right\} \cdot }\\ {{{\left[ {1 - \exp \left( { - {y^ * }/14} \right)} \right]}^2}.} \end{array} $ | (12) |
局部换热系数h,通过主流体的温度、局部壁面温度和局部的壁面热流密度来计算:
| $ {h_x} = \frac{{{q_{\rm{w}}}}}{{\left( {{T_{\rm{w}}} - {T_{{\rm{Tube}}}}} \right)}}, $ | (13) |
TTube通过管侧截面上的轴向速度、流体密度和局部流体温度来计算:
| $ {T_{{\rm{Tube}}}} = \frac{{\int_A {\rho uT{\rm{d}}A} }}{{{m_{\rm{b}}}}}, $ | (14) |
式中:ρ为局部流体密度/kg·m-3;u为局部轴向速度/(m·s-1);T为管侧局部流体温度/K。
2.3 其他计算细节本文涉及的CO2物性来源于NIST标准数据库,考虑了温度差异导致的密度、比热、黏度等热物性变化。针对超临界流动传热问题的特点,计算网格必须覆盖整个过渡层和黏性底层,为了满足该需求,需要对选定边界附近的区域进行网格加密,以保证近壁面附近网格y+ < 0.5[16-17],并获得相应的网格无关解。动量方程和能量方程的离散格式为QUICK格式,湍流方程的离散格式为二阶迎风格式,采用SIMPLEC算法求解Navier-Stokes方程。本文研究的超临界流体换热器存在2个进口面和2个出口面,流体进入换热段之前已充分发展。管侧内壁面和外壁面都采用无滑移边界条件,壁面温度通过耦合传热过程计算获得。当连续性方程、动量方程、k方程以及ε方程的残差小于10-6,同时壁面温度没有明显变化时,计算达到收敛。
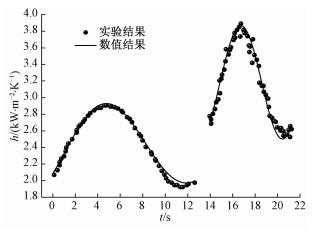
3 结果与讨论 3.1 模型验证由于目前尚无海洋条件下超临界流体传热流动的实验数据,并且作者在前期研究中已经证明本数学模型足以预测陆地条件下超临界流体的异常传热现象[14, 18],因此需要将海洋条件下单相流体的实验结果[19]与数学模型的预测结果进行对比,以验证本数学模型对海洋摇摆条件的预测性能。实验对海洋摇摆条件对直管内单相水加热过程中的传热和流动特性进行系列研究,管内径16 mm,管长1.2 m,距摇摆中心距离1.2 m,入口水温0~60 ℃,摇摆幅度范围10°~20°,摇摆周期7.5~12.5 s,更详细的实验细节见参考文献[20],该系列实验已被应用于数值仿真的验证工作[20]。图 2给出摇摆周期7.5和12.5 s时数值预测结果与实验结果的对比,从图中可以看出,实验结果和数值预测结果不仅在趋势上完全吻合,并且在量值上也非常接近,说明本文采用的数学模型可以对海洋摇摆条件进行准确的模拟。
|
Download:
|
| 图 2 数学模型预测结果与实验数据的对比 Fig. 2 Comparisons of calculated heat transfer coefficients with experimental data | |
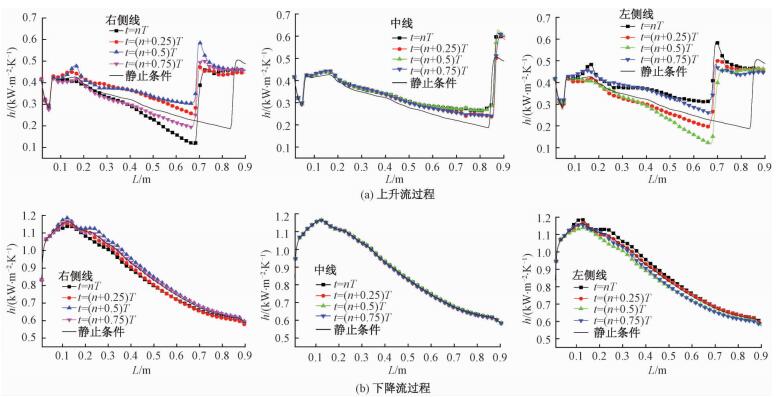
图 3给出摇摆条件和静止条件下超临界流体传热系数的变化规律。从图中可以看出,3条壁面线上均出现传热系数先降后升的现象,这说明管侧超临界流体在上升过程中出现明显的传热恶化与传热恢复现象。通过对比可以看出,3条壁面线上的传热系数分布与静止条件下存在明显差别,并3条线的传热系数也各自不同。中线处传热恢复的位置与静止工况非常接近,而其他2条线上传热恢复的位置相对前移,说明摇摆条件对左右两侧壁面的传热恶化现象有明显地抑制作用。由于摇摆运动的存在,左右两侧壁面传热系数会出现周期性变化,并且左右两侧壁面的传热系数的差值沿着管路逐渐增大,最大差值高达平均传热系数的120%。
|
Download:
|
| 图 3 摇摆条件和稳定条件下管侧换热系数的变化 Fig. 3 Local heat transfer coefficient distributions in steady state and rolling motion | |
对于下降流工况,3条壁面线上的传热系数均呈现出先升后降的现象,并且无论是静止条件还是摇摆条件,其传热系数均远大于上升流工况,说明下降流过程中超临界流体并没有发生传热恶化现象,这一点与陆地条件下的结果是相同的。另外,下降流过程中壁面传热系数也会出现类似于上升流工况中的周期性变化,但是其变化幅值远远小于上升流工况,因此,摇摆条件对下降流工况的影响远远小于上升流工况,摇摆条件下总传热量相对稳态工况降低0.2%。通过对比可以看出,摇摆条件对传热恶化现象的影响远大于非传热恶化现象,由于单相水不会发生传热恶化现象,因此摇摆条件对于管内单相水传热特性影响较小,但是对于容易发生传热恶化的超临界流体,摇摆条件对于其传热过程具有显著影响。
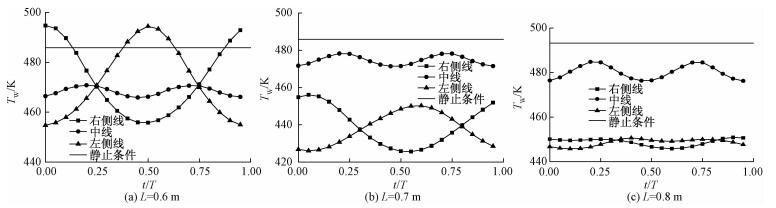
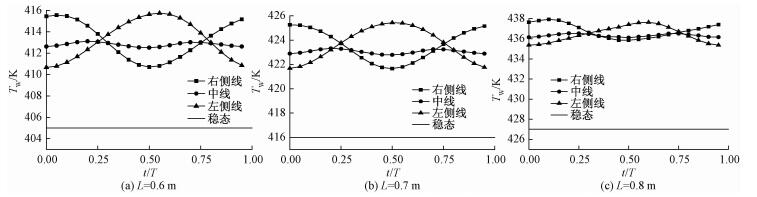
图 4给出上升流工况中局部壁面温度随时间的变化规律。从图中可以看出,壁面传热系数出现近似于三角函数式的周期性变化,当L < 0.7 m时,左右两线上的壁温变化幅度远远大于中线处,例如L=0.6 m时,中线壁温的振幅不超过5 K,而左右两线壁温的振幅超过40 K,该现象说明摇摆运动对左右两边壁面的影响大于其他位置。从图中还可以看出,随着流动的发展,左右两侧壁面率先出现传热恢复现象,壁面传热系数显著升高,此时左右两线的壁温明显小于中线,但依然存在明显的周期性变化。另外,值得注意的是,摇摆条件下的最高壁面温度比静止条件高10 K左右,但摇摆条件下平均壁面温度却比静止条件降低了约10 K,该现象说明摇摆条件虽然有利于抑制整体传热恶化现象,使总传热量增大7%,但也会导致局部壁面传热性能进一步减弱的现象,将会对管壁的安全性造成影响。
|
Download:
|
| 图 4 上升流过程中局部壁面温度随时间的变化 Fig. 4 Wall temperature for the upward flow | |
图 5给出下降流工况中局部壁面温度随时间的变化规律,下降流的管壁温度远小于对应的上升流工况,并且,其壁面温度随着流动的发展逐渐升高,但是依然远低于传热恶化现象时的壁面温度。另外,下降流过程的壁面温度振幅也远小于上升流过程,例如,L=0.6 m时左右侧壁温振幅为5 K,而中线处振幅仅为1 K。随着流动发展,壁面温度的振幅也逐渐减小,L=0.7 m时,壁温振幅降为4 K;L=0.8 m时,进一步降为3 K。该现象说明在超临界流体处于拟临界区时,摇摆条件对其传热特性的影响较为明显,而当超临界流体温度升高至远离拟临界区后,摇摆条件的影响逐渐减小。
|
Download:
|
| 图 5 下降流过程中局部壁面温度随时间的变化 Fig. 5 Wall temperature for the downward flow | |
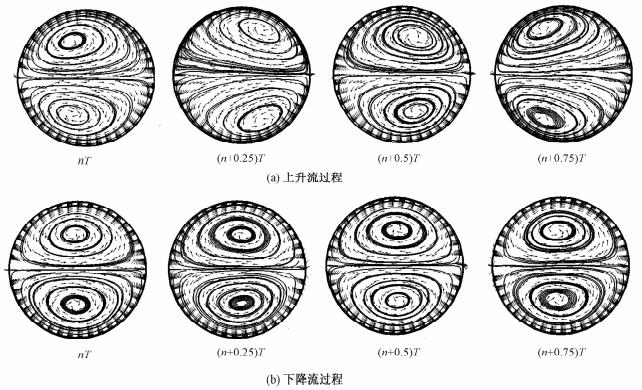
图 6给出上升流和下降流过程中L=0.6 m截面处管侧二次流的分布。从图中可以看出,在摇摆条件下管内的二次流是对称存在的,在管内形成上下两个相似的流向涡。由于摇摆条件下超临界流体的受力可以分解为轴向力和切向力,其中切向力的方向垂直于流动方向,可以导致管内流体发生偏转,形成二次流。在上升流过程中,由于周期性体积力和超临界流体物性的协同作用,截面中的二次流是不稳定的,即在周期性摇摆运动的影响下,随着时间的变化,流向涡从左侧运动至右侧,又从右侧运动到左侧,周而复始,因此宏观表现为壁面瞬态和时均传热系数与静止条件存在显著差别。而下降流过程中,二次流的位置随着时间的变化幅度不大,因此摇摆条件对下降流过程中超临界流体传热性能的影响相对较弱。这是由于上升流过程中超临界流体出现明显的传热恶化现象,导致近壁面附近流体密度与中心流体密度的插值增大,进一步增强了摇摆导致的体积力的作用。
|
Download:
|
| 图 6 管内L=0.6 m处二次流分布 Fig. 6 Vectors of secondary-flows in the cross section at L=0.6 m | |
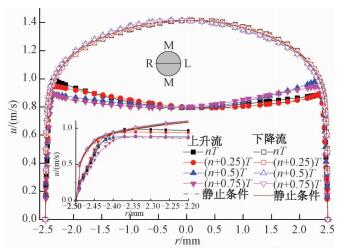
图 7给出不同流动方向下,L=0.6 m处管内典型位置(R-L线)的轴向速度变化,在上升流过程中,管内超临界流体速度分布呈现明显的M型分布,即近壁面附近流体的速度高于中心流,但是由于摇摆条件的存在,超临界流体速度的M型分布并不对称。这是由于近壁面附近的高温低密度流体在浮升力的作用下加速,导致最大轴向速度出现的位置向壁面移动。由于摇摆条件导致的周期性体积力作用,近壁面附近流体的最大速度也随着时间呈现出周期性的震荡,且震荡幅值超过截面平均速度的10%。但是,下降流过程中,轴向速度分布与静止条件下非常接近,轴向速度分布几乎不受摇摆条件的影响。
|
Download:
|
| 图 7 L=0.6 m处典型位置轴向速度的变化 Fig. 7 Axial velocity distributions in R-L line | |
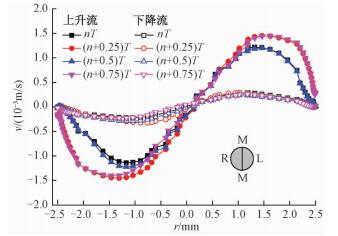
图 8给出不同流动方向下,L=0.6 m处管内典型位置(M-M线)切向速度的变化。从图中可以看出,上升流和下降流过程中管内的切向速度分布呈现明显的三角函数型,但上升流过程中的切向速度值远大于下降流,约为下降流切向速度的5倍。由于切向速度与摇摆运动产生的切向体积力有关,因此,上升流中切向力对流场的影响更加明显,这是由于上升流过程中严重的传热恶化现象导致的。
|
Download:
|
| 图 8 L=0.6 m处典型位置切向速度的变化 Fig. 8 Tangential velocity distributions in M-M line | |
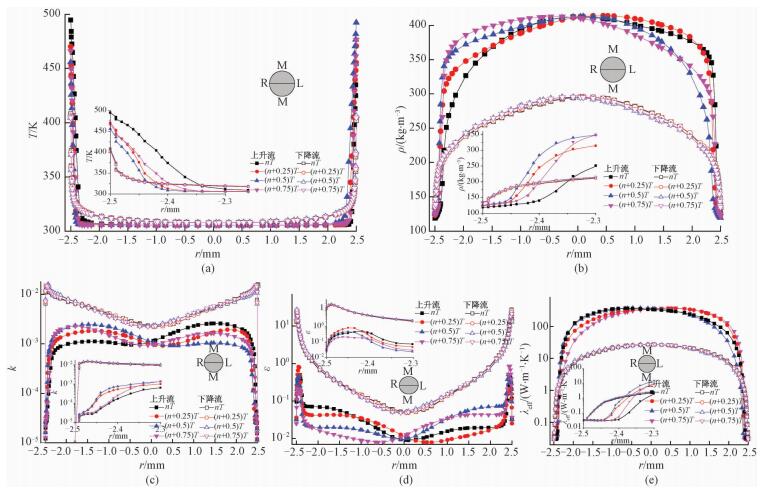
图 9给出L=0.6 m处R-L线上的超临界流体温度、密度和湍动场分布。从图中可以看出,在上升流过程中传热恶化现象意味着壁面温度的显著升高,导致近壁面附近流体温度随之升高。由于摇摆条件的影响,近壁面附近流体温度随着时间也呈现周期性变化。由于上升流过程中,传热恶化现象使壁面附近超临界流体密度剧烈降低,管内横截面密度分布不均匀性增强,摇摆条件导致的体积力随之增大。但是对于下降流过程,摇摆条件对于管内超临界流体的温度和密度分布几乎没有影响,不同时间的分布曲线几乎重合。
|
Download:
|
| 图 9 L=0.6 m处典型位置温度、密度和湍动场分布 Fig. 9 Fluid temperatures, properties, and turbulence fields at L=0.6 m in R-L line | |
从图 9(c)和9(d)可以看出,在上升流过程中,由于浮升力作用不仅导致近壁面附近流体加速,并且使中心流速度梯度降低,因此管内超临界流体湍动能和耗散率都受到明显抑制。并且,类似于轴向速度分布,在摇摆条件的影响下湍动能和耗散率分布也不对称。对于下降流过程,管内湍动能和耗散率均相对维持在一个较高的等级,这是由于超临界流体流动方向与浮升力方向相反,导致近壁面附近流体速度梯度增大,从而增强了湍动的产生和耗散。有效导热系数是流体导热系数和湍动导热系数之和,用来表征湍流流体的整体热传递能力。图 9(e)给出的上升流过程中近壁面附近流体的有效导热系数与流体的导热系数几乎相等,相比下降流过程小了1个量级,因此可以认为该处的湍动度几乎为零,流体传热主要是由流体分子之间的热扩散控制,并且该区域厚度相对较大,因此导致上升流过程中流体对流传热能力的急剧降低。
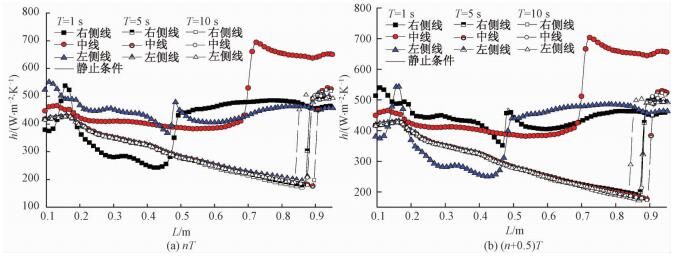
3.4 摇摆条件对超临界流体传热特性的影响为了研究不同海洋摇摆条件引起的附加力对超临界流体流动与传热特性的影响,图 10给出不同摇摆周期下的局部传热系数分布,摇摆幅值为25°,摇摆周期分别为1,2,5和10 s。从图中可以看出,当摇摆周期T=1 s,L < 0.5 m时,左右两侧壁面的传热系数存在显著的差异,该差值几乎达到静止条件下传热系数的60%;并且T=1 s时,左右两侧传热系数突升的位置(传热恶化减弱)向入口侧移动至L=0.5 m处,而静止条件下该现象出现在L=0.85 m附近。另外,T=1 s对应的中线壁面的传热系数整体高于静止条件,并且其峰值比静止条件高40%。但是随着摇摆周期的增大,超临界流体的宏观传热现象会出现明显的变化,例如:当摇摆周期大于5 s时,左右两侧和中线壁面附近的传热系数将非常接近,并且与静止条件下的传热系数吻合度很高。继续增大摇摆周期对局部壁面传热系数几乎没有影响,这说明此时摇摆条件下的附加力对超临界流体的传热过程几乎没有影响。以上这些现象表明,摇摆条件附加力对超临界流体传热过程的影响受摇摆强度的限制,即随着摇摆周期减小,超临界流体整体传热性能明显提升,如T=1 s时壁面平均传热系数比T=10 s时提高40%,且传热恶化现象影响范围减小50%。
|
Download:
|
| 图 10 摇摆周期对传热系数的影响 Fig. 10 Heat transfer coefficients for different rolling periods | |
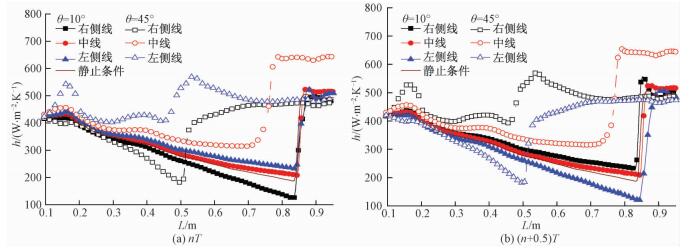
图 11给出不同摇摆幅值对壁面传热系数的影响,摇摆周期为2 s,摇摆幅值分别为10°,25°和45°。从图中可以看出,不同摇摆幅值下,超临界流体的传热系数呈现出显著差异。当摇摆幅值较小,如θ=10°时,摇摆条件对左右侧壁面传热系数存在周期性影响,其最大的传热系数变化幅值超过20%,该位置紧邻局部传热系数突升的位置,并且左右两侧和中线壁面处传热恶化消失的位置和量值与静止条件下的结果非常接近。当摇摆幅值较大,如θ=45°时,此时摇摆强度更加剧烈,产生了类似于小摇摆周期的现象,宏观表现为左右侧和中线位置传热传热系数突升的位置都有所前移,其平均传热系数相对θ=10°时增大30%。通过对比图 10和图 11可以看出,当摇摆周期较大时,左右两侧壁面传热系数振荡较小,而其传热系数突升的位置差异较大;而当摇摆幅值较小时,左右两侧壁面传热系数振荡明显,但其传热系数突升位置差异不大。总体而言,随着摇摆运动剧烈程度增大,即摇摆周期减小或摇摆幅值增大,摇摆条件的附加力对超临界流体的传热过程的影响也随之增大。
|
Download:
|
| 图 11 摇摆幅值对传热系数的影响 Fig. 11 Heat transfer coefficients for different rolling amplitudes | |
本文通过数值计算的方法研究海洋摇摆条件下超临界流体对流传热特性,主要结论如下:
1) 海洋摇摆条件下超临界流体依然会出现传热恶化现象,并且摇摆条件对拟临界区流体传热特性的影响远大于单相流体和远离拟临界区的超临界流体。
2) 摇摆条件会导致壁面传热系数的周期性振荡,左右两侧壁面的震荡幅值大于其他位置。
3) 超临界流体密度的不均匀分布有利于增强摇摆引发的体积力,有助于抑制传热恶化现象,并且摇摆运动对下降流过程的影响远远小于上升流过程。
4) 随着摇摆周期减小或者摇摆振幅增大,传热恶化现象逐渐减弱,值得关注的是摇摆运动可能会导致最高壁面温度增大从而影响管路的安全性。
| [1] |
Pendyala R, Jayanti S, Balakrishnan A R. Convective heat transfer in single-phase flow in a vertical tube subjected to axial low frequency oscillations[J]. Heat & Mass Transfer, 2008, 44(7):857–864.
|
| [2] |
贾辉, 谭思超, 高璞珍, 等. 摇摆引起的波动对单相自然循环换热的影响[J]. 核动力工程, 2010, 31(s1):44–48.
|
| [3] |
谭思超, 高璞珍, 苏光辉. 摇摆运动条件下自然循环复合型脉动的实验研究[J]. 原子能科学技术, 2008, 42(11):1007–1011.
|
| [4] |
Yan B H, Yu L. The experimental and theoretical analysis of a natural circulation system in rolling motion[J]. Progress in Nuclear Energy, 2012, 54(1):123–131.
DOI:10.1016/j.pnucene.2011.07.005 |
| [5] |
Chang S W, Huang B J. Thermal performances of corrugated channel with skewed wall waves at rolling and pitching conditions[J]. International Journal of Heat & Mass Transfer, 2012, 55(s 17/18):4548–4565.
|
| [6] |
林玮, 杨申音, 陈光明, 等. 船舶摇摆振动对传热和制冷系统的影响研究述评[J]. 制冷学报, 2014, 35(3):8–15.
|
| [7] |
Chen X, Wang G, Zhu Y, et al. Real-time simulation of ship motions in waves[M]//Advances in Visual Computing. Springer Berlin Heidelberg, 2012:71-80.
|
| [8] |
Tan S, Wang Z, Wang C, et al. Flow fluctuations and flow friction characteristics of vertical narrow rectangular channel under rolling motion conditions[J]. Experimental Thermal & Fluid Science, 2013, 50(6):69–78.
|
| [9] |
Wang C, Wang S, Wang H, et al. Investigation of flow pulsation characteristic in single-phase forced circulation under rolling motion[J]. Annals of Nuclear Energy, 2014, 64:50–56.
DOI:10.1016/j.anucene.2013.09.029 |
| [10] |
Xing D, Yan C, Sun L, et al. Effect of rolling motion on single-phase laminar flow resistance of forced circulation with different pump head[J]. Annals of Nuclear Energy, 2013, 54(54):141–148.
|
| [11] |
Kato Y, Nitawaki T, Muto Y. Medium temperature carbon dioxide gas turbine reactor[J]. Nuclear Engineering & Design, 2004, 230(1-3):195–207.
|
| [12] |
Moisseytsev A, Sienicki J J. Investigation of alternative layouts for the supercritical carbon dioxide Brayton cycle for a sodium-cooled fast reactor[J]. Nuclear Engineering & Design, 2009, 239(7):1362–1371.
|
| [13] |
He S, Kim W S, Jackson J D. A computational study of convective heat transfer to carbon dioxide at a pressure just above the critical value[J]. Applied Thermal Engineering, 2008, 28(13):1662–1675.
DOI:10.1016/j.applthermaleng.2007.11.001 |
| [14] |
Zhao Z, Che D. Numerical investigation of conjugate heat transfer to supercritical CO in a vertical tube-in-tube heat exchanger[J]. Numerical Heat Transfer Applications, 2014, 67(8):857–882.
|
| [15] |
He S, Kim W S, Bae J H. Assessment of performance of turbulence models in predicting supercritical pressure heat transfer in a vertical tube[J]. International Journal of Heat & Mass Transfer, 2008, 51(19/20):4659–4675.
|
| [16] |
Sharabi M, Ambrosini W, He S, et al. Prediction of turbulent convective heat transfer to a fluid at supercritical pressure in square and triangular channels[J]. Annals of Nuclear Energy, 2008, 35(6):993–1005.
DOI:10.1016/j.anucene.2007.11.006 |
| [17] |
Yang J, Oka Y, Ishiwatari Y, et al. Numerical investigation of heat transfer in upward flows of supercritical water in circular tubes and tight fuel rod bundles[J]. Nuclear Engineering & Design, 2007, 237(4):420–430.
|
| [18] |
Zhao Z, Che D, Wu J, et al. Numerical investigation on conjugate cooling heat transfer to supercritical CO2 in vertical double-pipe heat exchangers[J]. Numerical Heat Transfer, Part A:Applications, 2016, 69(5):512–528.
DOI:10.1080/10407782.2015.1081026 |
| [19] |
Tan S C, Su G H, Gao P Z. Heat transfer model of single-phase natural circulation flow under a rolling motion condition[J]. Nuclear Engineering & Design, 2009, 239(10):2212–2216.
|
| [20] |
Yan B H, Gu H Y. CFD analysis of flow and heat transfer of turbulent pulsating flow in a tube in rolling motion[J]. Annals of Nuclear Energy, 2011, 38(9):1833–1841.
DOI:10.1016/j.anucene.2011.05.020 |
 2018, Vol. 35
2018, Vol. 35 


