2. 天津大学中低温热能高效利用教育部重点实验室, 天津 300072;
3. 天津生态城能源投资建设有限公司, 天津 300480
2. Key Laboratory of Efficient Utilization of Low and Medium Grade Energy of Ministry of Education, Tianjin University, Tianjin 300072, China;
3. Tianjin Eco-city Energy Investment & Construction Co., Ltd, Tianjin 300480, China
近年来,温室效应已经成为全球性的环境与气候问题,其中,CO2对温室效应的贡献占70%左右。为此,政府间气候变化委员会(IPCC)提出利用碳捕捉与封存技术(carbon capture and storage, CCS)缓解温室气体问题。CCS技术是一项由CO2捕集、运输和封存组成的系统集成技术。为达到埋藏要求,对CO2进行捕集后必须进行分离,现有的CO2分离技术中,无论是发展较为成熟的胺吸收法,还是最具经济性优势的钙基吸收剂法,都需要对CO2与蒸汽的混合物进行进一步的提纯[1-2]。因此,研究含CO2的蒸汽的冷凝换热特性,对提纯CO2具有重要应用价值。
CO2在混合蒸汽凝结过程中以不凝气的形式存在。目前针对含不凝气的蒸汽膜状凝结建立的传热传质模型主要有以下几种:第1种是基于实验关联式的模型,即基于实验数据将凝结换热系数表示为关于不凝气质量分数、系统压力、温度等参数的函数关系式,这种模型的优点是易于通过编程实现,在允许误差范围内计算速度最高。第2种是扩散边界层模型,通过求解凝结液膜和气体边界层的控制方程,考虑两相流、流动状态以及液膜波动等因素对换热的影响,这种模型对含不凝气的蒸汽凝结已有较为深入的研究,精确度最高。部分学者[3-5]使用这种模型对自然对流以及受迫对流模式下的凝结换热进行探究。然而,由于计算时间较长,该模型一般只适用于稳态和二维情况的求解。第3种是传热和传质类比模型,利用传热传质相似理论分析气体扩散边界层和凝结机理,避开边界层内的控制方程,Maheshwari等[6]、Chantana和Kumar[7]以及Hogan等[8]针对不同工况下混合蒸汽的凝结换热进行了理论分析。
现有研究中不凝气多为空气,CO2作为不凝气的研究几乎没有。本文建立竖直表面双边界层模型,对含CO2的蒸汽在竖直平板上的凝结换热特性进行计算,探索CO2含量以及壁面过冷度对气、液膜的分布以及冷凝传热的影响。本文对于凝结换热理论的完善以及相关换热器的设计具有一定的借鉴意义。
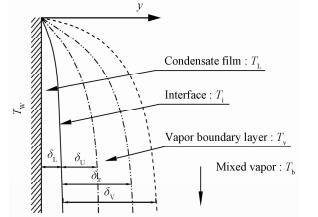
1 数值模型竖直表面双边界层模型如图 1所示。含不凝气的蒸汽发生冷凝时,蒸汽首先在冷却表面凝结并形成一层液膜。此时的界面不再是凝结壁面而是凝结液膜的最外层边界。凝结过程消耗了液膜附近的蒸汽浓度,而不凝气仍然存在,并逐渐积聚到较高浓度。由此两个边界层逐渐形成,一个是凝结液膜构成的液相边界层,另一个是紧挨着凝结液膜的气相边界层。并且由于不凝性气体积聚在气液界面,降低了气液界面的饱和温度Ti,使之低于主流蒸汽的饱和温度Tb。
|
Download:
|
| 图 1 双边界层理论模型示意图 Fig. 1 Diagram of the double boundary layer model | |
为简化模型,首先对模型求解进行几点假设:1)系统总压力保持恒定;2)主流混合蒸汽为饱和蒸汽;3)蒸汽在气液界面处发生凝结;4)凝结液膜和气体边界层内的传热传质为稳态;5)凝结液膜和气体边界层内的流动均为层流;6)凝结液膜内的温度分布为线性;7)忽略凝结液膜内的惯性力;8)理想气体假设;9)忽略气液界面热阻。
液膜动量方程,气膜内动量、能量方程以及不凝气扩散守恒方程如下:
| $ {\mu _{\rm{L}}}\frac{{{\partial ^2}{U_{\rm{L}}}}}{{\partial {y^2}}} + \left( {{\rho _{\rm{L}}} - {\rho _{\rm{V}}}} \right)g = 0, $ | (1) |
| $ {V_{\rm{V}}}\frac{{\partial {U_{\rm{V}}}}}{{\partial y}} = {\nu _{\rm{V}}}\frac{{{\partial ^2}{U_{\rm{V}}}}}{{\partial {y^2}}} + g\left( {1 - \frac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{V}}}}}} \right), $ | (2) |
| $ {V_{\rm{V}}}\frac{{\partial {T_{\rm{V}}}}}{{\partial y}} = {a_{\rm{V}}}\frac{{{\partial ^2}{T_{\rm{V}}}}}{{\partial {y^2}}}, $ | (3) |
| $ {V_{\rm{V}}}\frac{{\partial {W_{{\rm{nc}}}}}}{{\partial y}} = D \cdot \frac{{{\partial ^2}{W_{{\rm{nc}}}}}}{{\partial {y^2}}}. $ | (4) |
式中:U为x方向速度,V为y方向速度,v为动力黏度;ρ表示密度;a为热扩散系数,D为不凝气与蒸汽之间的扩散系数;下角标L表示液膜;V表示气膜;nc表示不凝气。
| $ 当y=0时:{U_{\rm{L}}} = 0,{T_{\rm{L}}} = {T_{\rm{w}}}. $ | (5) |
在气膜能量边界层,即y=δL+δT时:
| $ {U_{\rm{V}}} = 0. $ | (6) |
在气膜动量边界层,即y=δL+δU时:
| $ {T_{\rm{V}}} = {T_{\rm{b}}}. $ | (7) |
在气膜扩散边界层,即y=δL+δV时:
| $ {W_{{\rm{nc}}}} = {W_{{\rm{nc,b}}}}. $ | (8) |
在气液界面处,即当y=δL时:
| $ {U_{{\rm{L,i}}}} = {U_{{\rm{V,i}}}} = {U_{\rm{i}}}, $ | (9) |
| $ {\left( {{\mu _{\rm{L}}}\frac{{\partial {U_{\rm{L}}}}}{{\partial y}}} \right)_{\rm{i}}} = {\left( {{\mu _{\rm{V}}}\frac{{\partial {U_{\rm{V}}}}}{{\partial y}}} \right)_{\rm{i}}} = 0, $ | (10) |
| $ {T_{{\rm{L,i}}}} = {T_{{\rm{V,i}}}} = {T_{\rm{i}}}, $ | (11) |
| $ {\left( {{\lambda _{\rm{L}}}\frac{{\partial {T_{\rm{L}}}}}{{\partial y}}} \right)_{\rm{i}}} = \Delta {h_{\rm{V}}} \cdot m + {\left( {{\lambda _{\rm{V}}}\frac{{\partial {T_{\rm{V}}}}}{{\partial y}}} \right)_{\rm{i}}}, $ | (12) |
| $ {W_{{\rm{nc}}}} = {W_{{\rm{nc,i}}}}, $ | (13) |
| $ m = {\rho _{\rm{L}}}\frac{{\rm{d}}}{{{\rm{d}}x}}\int\limits_0^{{\delta _{\rm{L}}}} {{U_{\rm{L}}}{\rm{d}}y} . $ | (14) |
式中:T为温度;W为质量分数;δ为厚度;λ为导热系数;μ为运动黏度;m为凝结液量。下标i表示气液界面;w表示壁面;b表示主流混合蒸汽。
通过上述方程组及边界条件,最终可推导出液膜厚度、气膜厚度与气液界面温度三者之间的关系(详细推导过程可参考文献[9])如下:
| $ m = \frac{{{\rho _{\rm{V}}}D}}{{{\delta _{\rm{V}}}}}\ln \frac{{{W_{{\rm{nc,i}}}}}}{{{W_{{\rm{nc,b}}}}}} = \frac{{\left( {{\rho _{\rm{L}}} - {\rho _{\rm{V}}}} \right)g\delta _{\rm{L}}}^2}{{{\mu _{\rm{L}}}}}\frac{{{\rm{d}}{\delta _{\rm{L}}}}}{{{\rm{d}}x}}, $ | (15) |
| $ \begin{array}{*{20}{c}} {\frac{{\left( {{\rho _{\rm{L}}} - {\rho _{\rm{V}}}} \right)g\delta _{\rm{L}}}^2}{{2{\mu _{\rm{L}}}}} = \frac{g}{D}\ln \frac{{{W_{{\rm{nc,i}}}}}}{{{W_{{\rm{nc,b}}}}}}}\\ {\left\{ {1 - \frac{{{T_{\rm{i}}}\left[ {{M_{{\rm{nc}}}} - \left( {{M_{{\rm{nc}}}} - {M_{\rm{V}}}} \right){W_{{\rm{nc,i}}}}} \right]}}{{{T_{\rm{b}}}\left[ {{M_{{\rm{nc}}}} - \left( {{M_{{\rm{nc}}}} - {M_{\rm{V}}}} \right){W_{{\rm{nc,i}}}}} \right]}}} \right\}}\\ {\left\{ { - S{c^{\frac{1}{3}}} + Sc\ln \frac{{{W_{{\rm{nc,i}}}}}}{{{W_{{\rm{nc,b}}}}}}\left[ {{{\left( {\frac{{{W_{{\rm{nc,b}}}}}}{{{W_{{\rm{nc,i}}}}}}} \right)}^{Sc - \frac{2}{3}}} - 1} \right]} \right\}\delta _{\rm{V}}^2,} \end{array} $ | (16) |
| $ \begin{array}{*{20}{c}} {{\lambda _{\rm{L}}}\frac{{{T_{\rm{i}}} - {T_{\rm{w}}}}}{{{\delta _{\rm{L}}}}} = \left[ {{\rho _{\rm{V}}}D\Delta {h_{\rm{V}}} - {\lambda _{\rm{V}}}\frac{{{T_{\rm{b}}} - {T_{\rm{i}}}}}{{Le}} \cdot } \right.}\\ {\left. {\frac{1}{{\ln \left( {L{e^{ - \frac{2}{3}}}\ln \frac{{{W_{{\rm{nc,b}}}}}}{{{W_{{\rm{nc,i}}}}}}} \right) - 1}}} \right]\frac{{\ln \frac{{{W_{{\rm{nc,i}}}}}}{{{W_{{\rm{nc,b}}}}}}}}{{{\delta _{\rm{V}}}}}.} \end{array} $ | (17) |
通过迭代计算可求得气液界面温度Ti、液膜厚度δL以及气膜厚度δV,热流密度q为
| $ q = {\lambda _{\rm{L}}} \cdot \frac{{{T_{\rm{i}}} - {T_{\rm{w}}}}}{{{\delta _{\rm{L}}}}}. $ | (18) |
冷凝换热系数h为
| $ h = \frac{q}{{{T_{\rm{b}}} - {T_{\rm{w}}}}}. $ | (19) |
计算过程中,蒸汽以及CO2的相关物性可根据Nist Refprop 9.1获得。
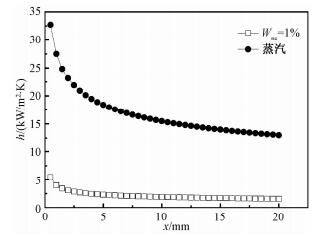
2 计算结果与讨论为说明CO2对冷凝过程的影响,本文首先对比分析纯蒸汽与含1%CO2的蒸汽凝结换热特性的差异,结果如图 2示。
|
Download:
|
| 图 2 CO2对蒸汽凝结换热的影响 Fig. 2 Effect of CO2 on condensation heat transfer of steam | |
与纯蒸汽相比,CO2的存在极大地削弱了蒸汽的凝结换热性能,如在x=10 mm处,冷凝换热系数由15.47 kW/(m2·K)降低到1.89 kW/(m2·K),减小87.8%。CO2作为不凝气,将会在冷凝液表面形成一层气膜,主流混合气体中的蒸汽要想完成冷凝必须穿过这层气膜,在气膜内越靠近气液界面,蒸汽分压越低,不凝气分压越高,因此不凝气的存在阻碍了蒸汽的运动,使得冷凝换热系数降低。此外,蒸汽到达气液界面时分压很小,不凝气浓度很大,此时界面处露点温度减小,冷凝驱动力亦减小,这也导致冷凝换热系数的降低。
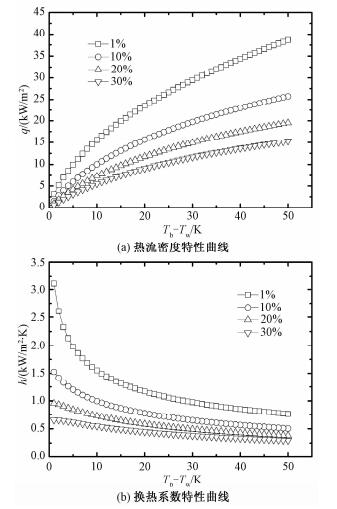
本文对比分析不同CO2浓度情况下凝结换热特性随过冷度的变化,结果如图 3所示。在CO2浓度一定时,随着过冷度的增加,热流密度逐渐增大,凝结换热系数逐渐减小。过冷度增大,说明壁面温度减小,冷凝驱动力增加,导致热流密度增大,而凝结换热系数是热流密度与过冷度的比值,由于热流密度并非线性增加,所以凝结换热系数不是定值,而是随过冷度的增大逐渐减小,这些与纯蒸汽的凝结换热特性基本相似。此外,从图中亦可以看出,随着CO2浓度的增大,凝结换热系数随过冷度的变化越来越平缓,即当高浓度CO2存在时,凝结换热系数基本上只与CO2浓度相关,随过冷度的变化很小,并在较大范围的过冷度内维持在一定水平,如当CO2浓度达到30%时,过冷度20~50 K范围内,凝结换热系数基本在300~440 W/(m2·K)之间。
|
Download:
|
| 图 3 含不同CO2浓度的蒸汽凝结换热特性 Fig. 3 Condensation heat transfer characteristics at different CO2 concentrations | |
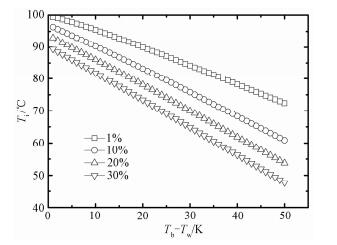
图 4给出不同CO2浓度情况下,界面温度随过冷度的变化。随着过冷度的增加,界面温度近乎线性降低,并且随着过冷度的增加,不同CO2浓度之间,界面温度的差距越来越大,如在过冷度10 K时,浓度1%与10%界面温度分别为95.46 ℃和90.32 ℃,差值为5.06 K,当过冷度增加到50 K时,界面温度变为72.38 ℃与60.86 ℃,差值增大到11.52 K。
|
Download:
|
| 图 4 不同过冷度下界面温度变化 Fig. 4 Variation in interface temperature with surface sub-cooling | |
过冷度对液膜厚度的影响规律如图 5所示。由图可知,随着过冷度的增加,液膜厚度逐渐增加。过冷度增加即壁面温度减小,虽然界面温度也在减小(如图 4所示),但是由于整体冷凝驱动力(Ti-Tw)是增加的,因此凝结换热量增大,凝结液生成量增加,液膜厚度增大。需要注意的是,在0~10 K过冷度范围内,液膜厚度增加速率明显较高,如不凝气浓度1%时,过冷度由0 K增加到10 K,液膜厚度增加0.25 mm,而10 K到50 K范围内,液膜厚度仅增加0.13 mm。此外,从图中可以看出,随着CO2浓度的增大,液膜厚度逐渐减小,这是因为CO2浓度越高,蒸汽分子运动到液膜表面的阻力越大,因此冷凝液量减少,液膜厚度变薄。
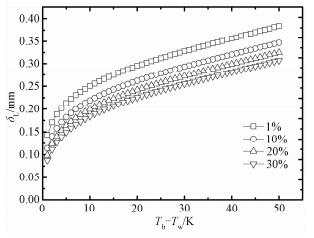
|
Download:
|
| 图 5 不同过冷度下液膜厚度变化曲线 Fig. 5 Variation in liquid film thicknesswith surface sub-cooling | |
图 6给出气膜厚度随过冷度的变化,从图中可以看出,气膜厚度要比液膜厚度大一个数量级,基本都在4 mm以上。与液膜厚度变化不同,过冷度越大,气膜厚度越小,这是因为过冷度的增大,使得冷凝液量增加了,因此需要气膜中蒸汽与不凝气的压力梯度增大,即气膜中不凝气浓度梯度增大,从而加速蒸汽的传质速率,使更多的蒸汽抵达液膜表面发生冷凝,因此需要气膜的厚度减小;但是过冷度的增加也会导致界面温度降低,即界面处蒸汽浓度降低,这会引起蒸汽浓度梯度增大,从而减缓气膜厚度的减小,二者综合作用下,气膜的厚度随过冷度的增加逐渐减小。此外,从图中亦可以看出,CO2浓度越高,气膜厚度越小,这也可从上述2个角度得到解释。
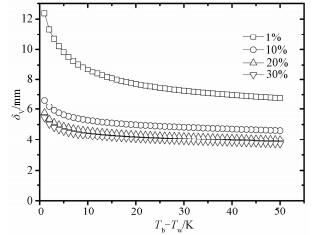
|
Download:
|
| 图 6 不同过冷度下气膜厚度变化曲线 Fig. 6 Variation in gas film thickness with surface sub-cooling | |
气膜热阻与液膜热阻的比值随过冷度的变化如图 7所示。随着过冷度的增加,该比值迅速减小至最小值,然后缓慢增加,这种变化趋势主要由界面温度的近乎线性变化引起。此外,随着CO2浓度的增大,该比值亦出现明显的增加,如在过冷度为20 K,CO2浓度由1%增大到30%时,该比值由0.95增大到5.48,这说明CO2浓度较高时,气膜热阻将成为主导热阻,因此在考虑强化混合蒸气的换热时,应更注重减小气膜侧的热阻。
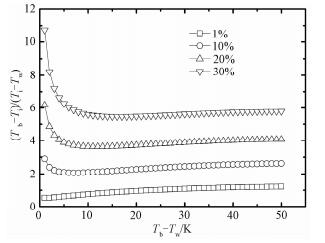
|
Download:
|
| 图 7 气膜热阻与液膜热阻的比值随过冷度的变化 Fig. 7 Resistance ratio of gas film to liquid film versus surface sub-cooling | |
本文基于双边界层理论建立含不凝气的蒸汽在竖直平板表面凝结换热模型,分析CO2存在对蒸汽凝结换热的影响,研究不同CO2浓度、不同表面过冷度条件下,凝结换热特性、界面温度以及气膜、液膜厚度等参数的变化情况,结果表明:
1) CO2的加入极大恶化蒸汽的凝结换热,随着过冷度的增加,热流密度逐渐增大,凝结换热系数逐渐减小,随着CO2浓度的增大,凝结换热系数随过冷度的变化越来越平缓,当不凝气浓度达到30%时,凝结换热系数基本在300~440 W/(m2·K)。
2) 过冷度的增加使得界面温度逐渐降低,并且界面温度随过冷度的变化几乎是线性的,随着过冷度的增加,不同CO2浓度情况下,界面温度的差距越来越大。
3) 随着过冷度的增加,液膜厚度逐渐增加,气膜厚度逐渐减小,但是气膜厚度比液膜厚度大一个数量级。随着CO2浓度增大,液膜厚度与气膜厚度均变小,但气膜热阻的比重逐渐增大,成为主导热阻。
| [1] |
Gouedard C, Picq D, Launay F, et al. Amine degradation in CO2 capture. I. A review[J]. International Journal of Greenhouse Gas Control, 2012, 10:244–270.
DOI:10.1016/j.ijggc.2012.06.015 |
| [2] |
Yin J Y, Qin C L, An H, et al. High-temperature pressure swing adsorption process for CO2 separation[J]. Energy & Fuels, 2012, 26:169–175.
|
| [3] |
Ambrosini W, Forgione N, Manfredini A, et al. On various forms of the heat and mass transfer analogy:discussion and application to condensation experiments[J]. Nuclear Engineering and Design, 2006, 236:1013–1027.
DOI:10.1016/j.nucengdes.2005.10.009 |
| [4] |
Dehbi A, Janasz F, Bell B. Prediction of steam condensation in the presence of noncondensable gases using a CFD-based approach[J]. Nuclear Engineering and Design, 2013, 258:199–210.
DOI:10.1016/j.nucengdes.2013.02.002 |
| [5] |
Maria P. Condensation of water vapor and acid mixtures from exhaust gases[D]. Germany: Technische Universität, 2004.
http://www.researchgate.net/publication/237759891_Condensation_of_Water_Vapor_and_Acid_Mixtures_from_Exhaust_Gases |
| [6] |
Maheshwari N, Saha D, Sinha R, et al. Investigation on condensation in presence of a noncondensable gas for a wide range of Reynolds number[J]. Nuclear Engineering and Design, 2004, 227:219–238.
DOI:10.1016/j.nucengdes.2003.10.003 |
| [7] |
Chantana C, Kumar S. Experimental and theoretical investigation of air-steam condensation in a vertical tube at low inlet steam fractions[J]. Applied Thermal Engineering, 2013, 54:399–412.
DOI:10.1016/j.applthermaleng.2013.02.024 |
| [8] |
Hogan K, Liao Y, Beeny B, et al. Implementation of a generalized diffusion layer model for condensation into MELCOR[J]. Nuclear Engineering and Design, 2010, 240:3202–3208.
DOI:10.1016/j.nucengdes.2010.05.059 |
| [9] |
彭文平. 汽-气凝结气、液膜厚度及换热特性的研究[D]. 北京: 华北电力大学, 2013.
http://d.wanfangdata.com.cn/Thesis/D528965 |
 2018, Vol. 35
2018, Vol. 35 


