单原子层二维材料(后文简称二维材料)具有优越的光学和电学性能,近年来受到广泛关注。例如,厚度仅有0.34 nm的石墨烯在可见光波段的吸收率约为2.3%,相当于厚度10 nm的硅或砷化镓的吸收率[1];单原子层二硫化钼(MoS2)由体相间接带隙半导体转变为直接带隙半导体[2]。因此,二维材料是有潜力的太阳能光伏电池材料[3-4]。提高二维材料光伏电池效率的关键是增大二维材料吸收率。已有研究将二维材料与纳米光子结构相结合,利用表面等离子共振效应[5]、光子晶体共振效应[6]等增强二维材料的吸收;但这些结构需要复杂的纳米加工工艺,不利于推广至实际应用。
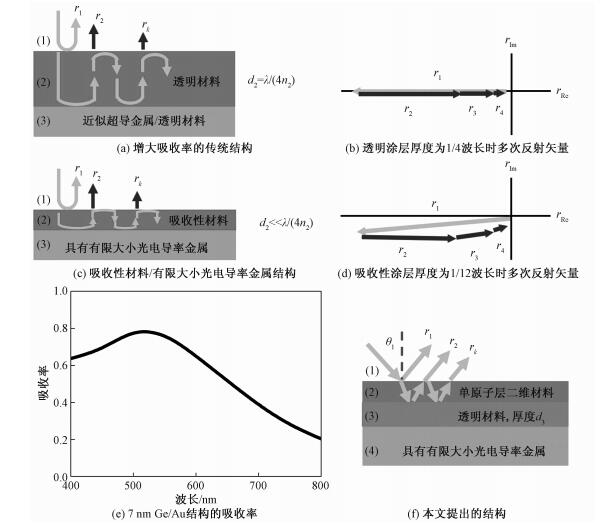
最近,Kats等[7]报道利用简单平面结构增强薄膜吸收特性的新机理,即非平凡干涉共振效应。传统的减小反射率、增大吸收率的结构是在近似超导金属或透明材料表面覆盖透明材料涂层,如图 1(a)所示。由于在1-2和2-3界面反射产生的相位差为π,因此只有当第2层厚度为1/4波长时,反射和传输产生的总相位差为2π,反射矢量形成封闭回路,从而减小反射率,如图 1(b)所示,1/4波长是涂层的最小厚度。如果将涂层换成吸收性材料,即复折射系数(m=n+iκ,n为折射率,κ为吸收指数)实部和虚部的大小为同一量级,将基底换成具有有限大小光电导率的金属(κ有限大小),如图 1(c)所示;此时,1-2和2-3界面反射产生的相位差不局限于π、并可以大于π。因此当涂层厚度远小于1/4波长时(即,平面超薄膜结构),虽然传输相位差减小,但反射和传输的总相位差仍近似为2π,反射矢量形成封闭回路,如图 1(d)所示。Kats等[7]采用简单的电子束蒸发方法在金(典型的具有有限大小光电导率的金属)基底上镀7 nm的锗(Ge,典型吸收性材料),测量共振波长处的吸收率达到0.8,如图 1(e)所示。
|
Download:
|
| 图 1 平面超薄膜结构及非平凡干涉共振效应 Fig. 1 Ultrathin planar film structure and non-trivial interference resonance | |
文献[7]及其后续研究中[8-9],吸收性材料厚度虽然小于1/4波长,但仍远大于典型二维材料的厚度。那么,吸收性材料的最小厚度究竟是多少?基于二维材料的平面超薄膜结构的吸收率能否达到100%?
1 问题描述已有工作[10]表明,非平凡干涉共振效应需满足相位同时在相平面的实轴和虚轴2个维度匹配,即r(rRe, rIm)=0,如图 1(d)所示;但只有一个可调变量,即吸收性超薄膜厚度;因而平面超薄膜结构的吸收特性对材料的固有属性依赖性强。
当吸收性材料采用二维材料时,二维材料厚度固定,因此需要引入2个可调参数,才可能突破结构吸收特性对材料属性的依赖,使吸收率达到100%。本文提出二维材料/透明材料/金属基底结构,如图 1(f)所示,引入透明材料厚度和入射角度2个可调参数,并计算分析这2个参数对结构吸收率的影响规律。图 1(f)所示4层结构反射系数为
| $ r = \frac{{{r_{12}} + {r_{234}}\exp \left[{{\rm{i}}\left( {4{\rm{ \mathsf{ π} /}}\lambda } \right){m_2}\cos {\theta _2}{d_2}} \right]}}{{1 + {r_{12}} {r_{234}}\exp \left[{{\rm{i}}\left( {4{\rm{ \mathsf{ π} /}}\lambda } \right){m_2}\cos {\theta _2}{d_2}} \right]}}, $ | (1) |
式中,
| $ {r_{234}} = \frac{{{r_{23}} + {r_{34}}\exp \left[{{\rm{i}}\left( {4{\rm{ \mathsf{ π} /}}\lambda } \right){m_3}\cos {\theta _3}{d_3}} \right]}}{{1 + {r_{23}}{r_{34}}\exp \left[{{\rm{i}}\left( {4{\rm{ \mathsf{ π} /}}\lambda } \right){m_3}\cos {\theta _3}{d_3}} \right]}}, $ | (2) |
对于入射角度为θ1的TE偏振光,
| $ {r_{pq}} = \frac{{{m_p}\cos {\theta _p}-{m_q}\cos {\theta _q}}}{{{m_p}\cos {\theta _p} + {m_q}\cos {\theta _q}}}, $ | (3) |
| $ {m_1}\sin {\theta _1} = {m_p}\sin {\theta _p}. $ | (4) |
式中:mp和dp分别为第p层材料的复折射系数和厚度。反射率R=|r|2,吸收率A=1-R。
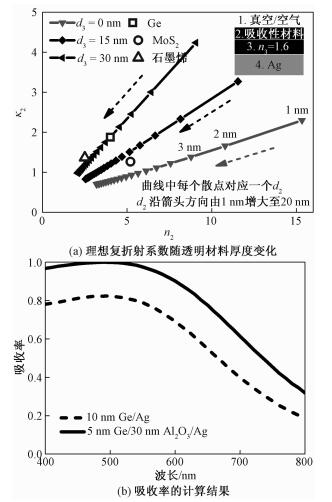
2 结果与讨论首先,本文证明:在同一波长产生共振时,添加透明材料层可使结构采用更小厚度的吸收性材料。不失一般性,透明材料采用氧化铝(Al2O3,n3=1.6),金属基底材料采用银(Ag,复折射系数采用文献[11]的结果)。图 2(a)所示结构达到完全吸收时满足
|
Download:
|
| 图 2 透明材料厚度对结构吸收率的影响 Fig. 2 Effects of the transparent layer thicknesses on optical absorption | |
| $ {r_{12}} + {r_{234}}\exp \left[{{\rm{i}}\left( {4{\rm{ \mathsf{ π} /}}\lambda } \right){m_2}\cos {\theta _2}{d_2}} \right] = 0. $ | (5) |
求解式(5)可计算得到吸收率为1时,吸收性材料的理想复折射系数。图 2(a)为θ1=0°、波长500 nm、吸收性材料厚度(d2)范围1~20 nm及透明材料厚度(d3)范围0~30 nm时的计算结果。本文称d3=0 nm条件下理想复折射系数曲线为基线。结果表明,采用图 1(c)所示结构,吸收性材料复折射系数需落在基线上才能达到完全吸收;但自然界中满足该条件的材料有限,例如图 2(a)中Ge在500 nm的复折射系数(采用Liu等[12]的结果)即不满足,进一步说明图 1(c)所示结构的吸收特性依赖材料固有属性。
从图 2(a)还可以看出,添加透明材料层结构的理想复折射系数曲线均在基线上方,因而只要吸收性材料的复折射系数在基线上方(例如Ge),一定存在一个透明材料厚度,使得结构吸收率为1。例如,对Ge而言,d2=5 nm、d3=30 nm时,结构吸收率为1(如图 2(a)所示)。同时,曲线斜率随着透明材料厚度的增大而增大,表明在同一波长产生共振时,添加透明材料层可使结构采用更小厚度的吸收性材料。为验证上述分析,本文计算10 nm Ge/Ag和5 nm Ge/30 nm Al2O3/Ag结构的吸收率(反射率)。如图 2(b)所示,2种结构均在波长500 nm产生共振效应,5 nm Ge/30 nm Al2O3/Ag结构的峰值吸收率大于0.99,且Ge的厚度只有10 nm Ge/Ag结构的一半,结果与图 2(a)吻合。
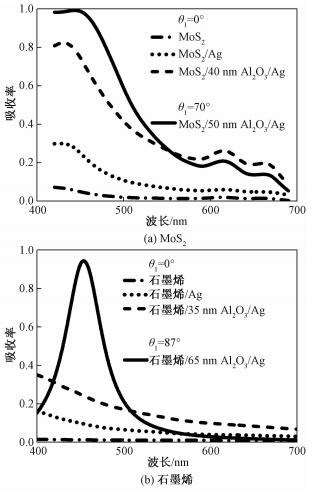
从上述结果可以预期,采用图 1(f)所示结构可以增大二维材料的吸收率。本文以MoS2(厚度d2=0.65 nm,复折射系数采用文献[13]的结果)和石墨烯(d2=0.34 nm,复折射系数采用文献[14]结果)为例,分别计算单层二维材料、二维材料/Ag以及二维材料/Al2O3/Ag 3种结构的法向吸收率。不失一般性,本文考察这3种结构在450 nm波长的法向吸收率。图 3(a)中,二维材料/Al2O3/Ag结构的Al2O3厚度采用如下方法确定:计算Al2O3厚度0~500 nm范围内变化时,二维材料/Al2O3/Ag结构450 nm波长的法向吸收率,取最大吸收率对应的Al2O3厚度。
|
Download:
|
| 图 3 二维材料平面超薄膜结构的吸收率 Fig. 3 Optical absorption of ultrathin planar films using 2D materials | |
如图 3(a)所示,由于厚度只有0.65 nm,单层MoS2的法向吸收率在450 nm只有0.05,在420~690 nm整个波段均小于0.1;MoS2/Ag结构可产生非平凡干涉共振效应,因而吸收率增大,450 nm波长处,法向吸收率由0.05增大至0.25;添加40 nm Al2O3使非平凡干涉共振效应进一步增强,MoS2/40 nm Al2O3/Ag结构的吸收特性显著增强,450 nm波长处法向吸收率进一步增大至0.75。对于石墨烯可得到相同规律,如图 3(b)所示。但是由于法向入射条件下,二维材料/Al2O3/Ag结构只有透明材料厚度一个可调参数,无法满足2个维度的完全吸收条件,因而吸收率无法达到100%,尤其石墨烯/35 nm Al2O3/Ag结构450 nm波长的法向吸收率只有0.25。
因此接下来,本文证明:一定存在一个入射角度,使二维材料/Al2O3/Ag结构吸收率达到100%。图 4(a)为波长450 nm、d3=50 nm(图 4(b)中,d3=65 nm)、d2范围0.1~1 nm以及θ1范围0°~87°条件下,吸收性材料理想复折射系数的计算结果。本文称θ1=0°时理想复折射系数曲线为基线。结果表明,随入射角度增大,理想复折射系数曲线向基线下方移动,因而只要吸收性材料的复折射系数在基线下方(例如MoS2和石墨烯),一定存在一个入射角度,使得结构吸收率为1。例如,对于MoS2(石墨烯),d3=50 nm(65 nm)、θ1=70°(87°)时,结构吸收率近似为1(如图 4(a)和(b)所示)。为验证上述分析,本文计算MoS2/50 nm Al2O3/Ag结构对70°入射光的吸收率以及石墨烯/65 nm Al2O3/Ag对87°入射光的吸收率,如图 3(a)和(b)所示。2种条件下,波长450 nm的吸收率超过0.97,比单层二维材料的吸收率提高2个数量级。

|
Download:
|
| 图 4 理想复折射系数随入射角度的变化 Fig. 4 Variation of ideal complex refractive index with incident angle | |
从应用角度看,具有宽波段、广角度高吸收特性的二维材料吸收器更有应用价值,作者今后将开展进一步研究。二维材料能否应用于太阳能电池还需要考虑其结构强度和稳定性。对于单晶硅、非晶硅、GaAs等常规半导体材料,当其厚度小于10 nm时,薄膜相比其体材料缺陷变多,强度降低、更易碎,电子-空穴对体相复合损失增大;同时,由于表面存在悬空化学键,材料更易氧化,电子-空穴对表面复合损失增大[15]。单层或多层二维材料由范德瓦耳斯力结合,固有特性使其不存在上述问题,因此,具有更优越的效率、强度和稳定性,在空间发电系统、可穿戴光电子器件等对太阳能电池的重量、柔性有特殊要求的领域有良好应用前景[15]。
3 结论本文研究基于单原子层二维材料的、具有简单平面薄膜结构的吸收器吸收特性。平面薄膜结构完全吸收需满足2个维度的匹配条件(r(rRe, rIm)=0),因此,本文引入透明材料厚度和入射角度2个可调参数,提出二维材料/透明材料/金属基底结构。理论和实验研究表明,一定存在一对透明材料厚度值和入射角度值使结构吸收率达到100%。本文以MoS2和石墨烯为例,通过设计使MoS2/50 nm Al2O3/Ag结构对70°入射光的吸收率以及石墨烯/65 nm Al2O3/Ag对87°入射光的吸收率超过0.97,比单层二维材料吸收率提高2个数量级。研究结果可为二维材料在太阳能光伏转换中的应用提供理论指导。
| [1] |
Bernardi M, Palummo M, Grossman J C. Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials[J]. Nano Letters, 2013, 13(8):3664–3670.
DOI:10.1021/nl401544y |
| [2] |
Mak K F, Lee C, Hone J, et al. Atomically thin MoS2:a new direct-gap semiconductor[J]. Physical Review Letters, 2010, 105(13):136805.
DOI:10.1103/PhysRevLett.105.136805 |
| [3] |
Furchi M M, Pospischil A, Libisch F, et al. Photovoltaic effect in an electrically tunable van der Waals heterojunction[J]. Nano Letters, 2014, 14(8):4785–4791.
DOI:10.1021/nl501962c |
| [4] |
刘东, 于海童, 杨震, 等. 全碳太阳能热光伏系统[J]. 工程热物理学报, 2015, 36(4):698–702.
|
| [5] |
Zhao B, Zhang Z M. Strong plasmonic coupling between graphene ribbon array and metal gratings[J]. ACS Photonics, 2015, 2(11):1611–1618.
DOI:10.1021/acsphotonics.5b00410 |
| [6] |
Piper J R, Fan S H. Broadband absorption enhancement in solar cells with an atomically thin active layer[J]. ACS Photonics, 2016, 3(4):571–577.
DOI:10.1021/acsphotonics.5b00510 |
| [7] |
Kats M A, Blanchard R, Genevet P, et al. Nanometre optical coatings based on strong interference effects in highly absorbing media[J]. Nature Materials, 2013, 12(1):20–24.
DOI:10.1038/nmat3443 |
| [8] |
Long Y, Su R, Wang Q, et al. Deducing critical coupling condition to achieve perfect absorption for thin-film absorbers and identifying key characteristics of absorbing materials needed for perfect absorption[J]. Applied Physcis Letters, 2014, 104(9):091109.
DOI:10.1063/1.4867646 |
| [9] |
Kats M A, Byrnes S, Blanchard R, et al. Enhancement of absorption and color contrast in ultra-thin highly absorbing optical coatings[J]. Applied Physcis Letters, 2013, 103(10):101104.
DOI:10.1063/1.4820147 |
| [10] |
Liu D, Yu H T, Yang Z, et al. Ultrathin planar broadband absorber through effective medium design[J]. Nano Research, 2016, 9(8):2354–2363.
DOI:10.1007/s12274-016-1122-x |
| [11] |
Palik E D.
Handbook of optical constants of solids I[M]. New York: Academic Press, 1985: 350-357.
|
| [12] |
Liu D, Yu H T, Duan Y Y, et al. New insight into the angle insensitivity of ultrathin planar optical absorbers for broadband solar energy harvesting[J]. Scientific Reports, 2016, 6:32515.
DOI:10.1038/srep32515 |
| [13] |
Li Y, Chernikov A, Zhang X, et al. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides:MoS2, MoSe2, WS2, and WSe2[J]. Physical Review B, 2014, 90(20):205422.
DOI:10.1103/PhysRevB.90.205422 |
| [14] |
Gray A, Balooch M, Allegret S, et al. Optical detection and characterization of graphene by broadband spectrophotometry[J]. Journal of Applied Physics, 2008, 104(5):053109.
DOI:10.1063/1.2974096 |
| [15] |
Jariwala D, Davoyan A, Tagliabue G, et al. Near-unity absorption in van der Waals semiconductors for ultrathin optoelectronics[J]. Nano Letters, 2016, 16(9):5482–5487.
DOI:10.1021/acs.nanolett.6b01914 |
 2018, Vol. 35
2018, Vol. 35 


