2. 安徽工业大学数理科学与工程学院, 安徽 马鞍山 243032
2. School of Mathematics and Physics, Anhui University of Technology, Ma'anshan 243032, Anhui, China
随着现代科技的发展,对所需单晶材料的质量要求也越来越高。浮区晶体生长法因为其无坩埚接触污染这一优点,已经成为当今工业生产单晶材料的重要技术,广泛用于高精度硅、高温合金及其他半导体材料的生长。在常重力情况下,浮区法生长的体单晶尺度较小,并且浮力对流的强度较热毛细对流大很多,导致热毛细对流被其覆盖。然而在微重力情况下,热毛细对流成为熔体内主要对流方式,所以研究热毛细对流的特点对未来生产大尺寸高质量的体单晶具有重要意义。自从1976年Chang和Wilcox[1]发现热毛细对流对浮区晶体生长的影响后,人们对热毛细对流展开了广泛的研究。Levenstam和Amberg[2]以Re数为参变量,研究高径比等于1的圆柱形液桥的表面张力的失稳过程。结果表明,随着Re数的不断增加,二维定常轴对称的对流会向三维对流转换,然后进一步转换为振荡的对流。Bazzi等[3]以Ma数为参变量分析高径比为0.7时低Pr数液桥对流的稳定性。研究发现,Ma=48是液桥出现第1次失稳的临界值;Ma =80是液桥第2次失稳的临界值。张银等[4]研究不同温差对大尺度液桥自由表面变形的影响。研究结果显示:在较大的温差作用下,液桥内热毛细对流呈现三维不稳定振荡;微重力情况下,液桥自由表面在冷、热壁面附近会膨胀,中间部分收缩,液桥变得类似于“瓶颈”状结构。Huang等[5]分析液桥内热毛细对流对杂质扩散的影响。数值结果表明,受热毛细对流的影响,熔体中的杂质呈各向异性分布,子午面上杂质浓度等值线呈“哑铃”状,而横切面上的浓度等值线呈“星形”结构,并且径向分凝效应随Ma数的增大而增大。因此,有必要深入研究熔体中的传热流动特性并对其进行有效控制,以提高单晶品质。由于硅等半导体熔体具有良好的导电性,通过外加磁场可有效地抑制熔体流动并影响热量传递,从而减少晶体的生长条纹,控制晶体生长的界面、杂质的分离等。各种外部磁场中,旋转磁场具有低功耗的特点,其产生洛伦兹力能够增加传质速率,使熔体的运动稳定,施加旋转磁场对导电熔体进行主动控制是可行有效的。
目前为止,旋转磁场已广泛用于Czochralski法[6]、LPD法[7]、Bridgman法[8]及浮区法[9-10]等晶体生长中,相应的理论分析及实验研究业已展开,取得了一定的成果。但是大多数学者的研究是针对熔体振荡被完全控制的情况,对熔体被完全抑制前对流的过渡状态鲜有报道。鉴于理论分析和实验研究在高温条件下存在的困难,本文采用数值模拟为主要手段,完整复现旋转磁场作用下不同加热温差时浮区中硅熔体的传热流动特性,揭示不同加热功率对晶体生长的影响机制,研究结果可对浮区法晶体生长中确定有效的磁场强度提供帮助。
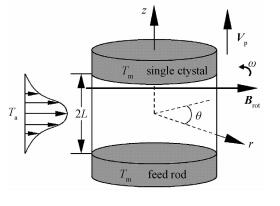
1 物理数学模型本文计算采用柱坐标系(r, θ, z)下的全浮区模型,物理模型如图 1所示。在微重力条件下,不考虑自由面的变形,即认为熔区自由面为圆柱面,整个熔区高为2L,悬浮在具有相同半径R的圆柱状单晶棒和多晶棒之间,由外部环形加热器进行辐射加热。生长界面和熔化界面简化为平面,分别位于z=L和z=-L,并保持熔点温度Tm不变。环境温度分布假设为Gauss分布[11]:
|
Download:
|
| 图 1 物理模型 Fig. 1 Physical model | |
| $ {T_{\rm{a}}} = {T_{\rm{m}}} + \Delta T\exp \left[{-{{\left( {\frac{z}{a}} \right)}^2}} \right], $ |
式中:ΔT为环形加热器温度和熔点温度之差;a是温度分布的尺度参数;自由表面上最大温度记为Tmax。晶体生长速度沿z轴正向,大小为Vp。假设熔体为不可压缩的牛顿型黏性流体,表面张力作用在自由表面上。除流体表面张力外,流体的其他物性参数保持不变。熔体自由表面上的表面张力为温度的线性函数,表示为
| $ \sigma = {\sigma _{\rm{m}}}-{\gamma _{\rm{T}}}\left( {T-{T_{\rm{m}}}} \right), $ |
式中,γT=-(∂σ/∂T)>0。施加的外部旋转磁场强度和角频率分别为B0和ω,其分布[10]可表示为
| $ {\mathit{\boldsymbol{B}}_{{\rm{rot}}}} = {B_0}\left[{\cos \left( {\omega t} \right){\mathit{\boldsymbol{e}}_\theta }-\sin \left( {\omega t} \right){\mathit{\boldsymbol{e}}_t}} \right] $ |
式中,eθ和er分别是轴向和径向单位矢量。
基于以上假设,外加旋转磁场作用下,熔区内控制方程可表示为:
| $ \nabla \cdot \mathit{\boldsymbol{V}} = 0, $ | (1) |
| $ \frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial t}} + \left( {\mathit{\boldsymbol{V}} \cdot \nabla } \right)\mathit{\boldsymbol{V =-}}\frac{1}{\rho }\nabla P + \frac{\mu }{\rho }{\nabla ^2}\mathit{\boldsymbol{V + }}\frac{{{\mathit{\boldsymbol{f}}_{{\rm{rot}}}}}}{\rho }, $ | (2) |
| $ \frac{{\partial T}}{{\partial t}} + \left( {\mathit{\boldsymbol{V}} \cdot \nabla } \right)T = \alpha {\nabla ^2}T. $ | (3) |
式中:∇和∇2是在柱坐标系下的算符;V是速度矢量;T为熔体温度;ρ为密度;P为压力;μ为动力黏度;α为热扩散系数。旋转磁场在熔体内部产生的洛伦兹体积力[12]可表示为frot=σeB02ωreθ/2,其中σe为电导率。
边界条件和初始条件:
| $ 当z = \pm L时, T = {T_{\rm{m}}}, \mathit{\boldsymbol{V = }}{\mathit{\boldsymbol{V}}_{\rm{p}}}; $ | (4-a) |
| $ \begin{array}{l} 当r = R时, -\kappa \frac{{\partial T}}{{\partial r}}\varepsilon {\sigma _0}\left( {{T^4}-T_{\rm{a}}^4} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;{\rm{ \mathsf{ μ} }}\frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial \mathit{\boldsymbol{n}}}}={\gamma _{\rm{T}}}\nabla T; \end{array} $ | (4-b) |
| $ 当t = 0时, T = {T_{\rm{m}}}, \mathit{\boldsymbol{V = }}{\mathit{\boldsymbol{V}}_{\rm{p}}}. $ | (4-c) |
式中:κ热传导系数,σ0是Stefan-Boltzmann常数,ε是黑体系数,n是自由表面的法向单位矢量。
硅熔体各物性参数的设定如表 1所示,其他计算所需参数及无量纲数Prandtl数
|
|
表 1 硅熔体物性参数及其他计算所需参数 Table 1 Properties of the Si melt and the system |
采用网格量为40r×120θ×80z的非均匀结构化交错网格的有限体积法对控制方程进行空间离散,并在自由表面及交界面附近进行局部加密,网格的独立性已得到验证(见表 2)。计算中采用时间步长为10-3 s。对动量方程、能量方程中的对流项采用QUICK格式离散,扩散项都采用二阶中心差分离散,时间项采用二阶隐式推进法,压力速度耦合采用PISO算法。算法的正确性同Levenstam和Amberg[2]以及Li和Wu[11]的结果进行了比较。表 3显示的是当Pr=0.01, Re=3 500时,相同模型下熔体中最大速度值和周向最大速度值同文献[2]的对比结果,可以看出,二者吻合得较好;当温差很小时,对于小Pr数的半导体晶体生长而言,流场结构对温度场的影响很小,通过定性比较发现,本文熔体子午面上温度分布与文献[11]中二维模型温度分布一致。
|
|
表 2 ΔT=20 K时不同网格下熔体中最大速度及最大周向速度 Table 2 Maximal velocities of the thermocapillary flow (ΔT=20 K without magnetic field) for different meshes in the floating zone |
|
|
表 3 本文和Levenstam et al.[2]的计算结果对比 Table 3 Comparison between the present results and the results of Levenstam et al. |
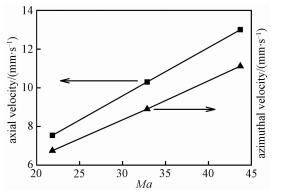
由于半导体具有良好的导电性,旋转磁场所产生的洛伦兹力,一方面对熔体产生周向的搅拌作用,同时对浮区内轴向流动具有抑制作用,这两种作用都将对熔体内的对流产生影响。为此本文中对不同辐射温度下的熔体施加角频率ω =2π×50的均匀旋转磁场,研究磁场作用时不同表面张力下熔区的对流结构及演化规律。选取ΔT分别为20、30和40 K的3种情况,从计算结果看,当ΔT从20 K增加到40 K时,熔体温度最大值均出现在自由表面中部即z=0截面边缘附近,3种情况下温度最大值Tmax分别为1 684.11、1 684.66和1 685.21 K,对应Ma数为21.8、32.9和43.7。图 2描述熔体在不同辐射温度下,1 mT的旋转磁场作用下的周向最大速度和轴向最大速度变化曲线。从图中可以看出,当外加旋转磁场不变,Ma数增大,熔体的周向速度和轴向速度均随之增加,并且随着Ma数的增大,熔体周向最大速度和轴向最大速度近似为线性增长。
|
Download:
|
| 图 2 熔体内周向最大速度和轴向最大速度随Ma数变化曲线(1 mT, 50 Hz) Fig. 2 Variations in the maximal azimuthal velocity and axial velocity with Ma number under RMF (1 mT, 50 Hz) | |
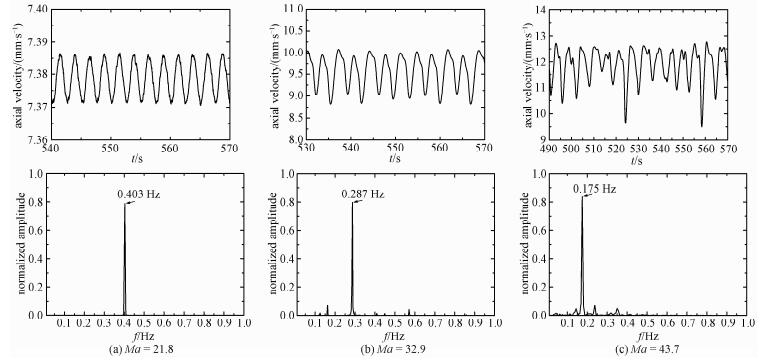
图 3是B0=1 mT时不同Ma数下z=0切面上的轴向速度分布。当Ma=21.8(图 3(a))时,轴向速度呈三涡胞对称分布,其周向波数m=3;随着Ma数的增加,当Ma =32.9(图 3(b))和43.7(图 3(c))时,其周向波数分别为m=2和m=1。图 3显示,速度等值线在涡胞中心附近时形成闭合的曲线,而在自由表面附近时则没有形成闭合的曲线,每个涡胞像个蝌蚪一样后面有条尾巴,这是由于磁场对熔体的周向搅拌作用的结果。那么,一个有趣的问题呈现面前,既然熔体是旋转的,那么旋转后的熔体是不是振荡的呢?为此我们对自由表面上关于中截面z=0对称的两点P1和P2进行了监测。图 4描述磁场作用下,不同Ma数时熔体表面监测点P1(0.01 m,0,0.004 m)处的轴向速度随时间的演变,及其对应的快速傅里叶变换的频谱图。从图 4可以看出,1 mT的旋转磁场作用下,P1点的轴向速度随时间均呈周期性变化,其振荡主频分别为0.40、0.29和0.18 Hz。不难发现,随着表面张力流的增强,熔体对流的振荡频率逐渐降低,并与Ma数成线性关系。此外,研究发现,P1点的对称点P2的轴向速度随时间也呈周期性振荡,其频谱图和P1的频谱图一样,表明1 mT的均匀旋转磁场作用下,熔体对流为全局振荡而不是局部振荡。

|
Download:
|
| 图 3 B0=1 mT时不同Ma数下中截面z=0的轴向速度等值线 Fig. 3 Axial velocity isolines at the middle plane z=0 under 1 mT RMF for different Ma numbers | |
|
Download:
|
| 图 4 不同Ma数时监测点P1(0.01 m,0,0.004 m)处的轴向速度随时间的演变及其快速傅里叶变换的频谱图(1 mT, 50 Hz) Fig. 4 Axial velocity evolution with time (up) and the fast Fourier transform spectrum (down) at P1(0.01 m, 0, 0.004 m) under 1mT RMF for different Ma numbers | |
通过对P1点温度的监测发现,当Ma =21.8时,虽然熔体内对流呈现周期性振荡模式,但是P1点温度基本不发生变化,这是由于表面张力流强度较弱,表面温度梯度本来就很小的缘故。随着Ma数的增加,表面张力流随之增加,当Ma=32.9和43.7时,P1点的温度随时间呈现周期性振荡,对其频谱图分析发现其振荡频率与对流振荡频率基本相同,如图 5所示。

|
Download:
|
| 图 5 Ma =32.9和43.7时监测点P1的温度随时间变化的频谱图(1 mT, 50 Hz) Fig. 5 Fast Fourier transform (FFT) spectra at point P1 under 1 mT RMF for Ma =32.9(a) and Ma=43.7(b) | |
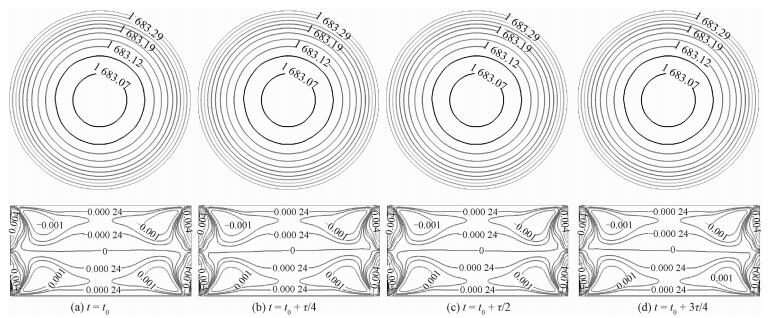
图 6~图 8分别描述1 mT的旋转磁场作用下,不同Ma数时熔体z=4 mm截面上的温度等值线和θ=0切面上的轴向速度等值线在一个振荡周期内的演化过程。分析发现,当Ma=21.8时,熔体内的温度分布主要由扩散决定,对流对温度分布影响甚微,温度场不随时间变化。这一点从z=4 mm截面温度呈中心对称分布得以验证,温度等值线成一系列同心圆环,并且由内自外温度逐渐升高,如图 6所示。从θ=0切面的轴向速度分布看出,除中截面z=0附近区域,熔体中上下两部分轴向速度关于z=0镜面对称,由表面张力形成的两对对流涡的涡心在自由表面附近,熔体大部分区域被4个对称的逆向对流涡占据。图 7显示,当Ma数升高到Ma=32.9时,z=4 mm切面上的温度等值线均呈现旋转180°重合。熔体温度在自由表面附近形成一对冷区和一对热区,且随时间做逆时针旋转。熔体中的轴向速度不再关于z=0镜面对称,在一个振荡周期内,上下部的对流涡胞交替增大,从图 7中θ=0切面轴向速度分布可见,对流涡胞基本上左右对称,这种左右对称的对流涡胞结构是其与Ma=21.8时共有的。当Ma=43.7时,从图 8中可以观察到,熔体z=4 mm切面上的温度具有相同的单涡分布结构,且随时间做逆时针旋转。与上述两种情况相比,Ma=43.7时的熔体轴向速度和温度分布有较大的变化。由θ=0切面轴向速度分布可以看出,Ma=43.7时左右对称的对流涡胞结构消失,演化为切面上两对角处对流涡胞交替增大的结构;此时,熔体z=4 mm切面上轴向速度大的区域(例如自由表面附近)的温度分布不再呈现出中心对称的性质,说明熔体的温度分布和轴向速度分布密切相关。
|
Download:
|
| 图 6 Ma=21.8时z=4 mm截面上的温度和θ =0切面上的轴向速度在一个振荡周期(τ=2.5 s)内的演化过程(1 mT, 50 Hz) Fig. 6 Temperature isolines at z=4 mm (up) and axial velocity isolines at θ =0(down) in one period (τ=2.5 s) under 1 mT RMF for Ma=21.8 | |
|
Download:
|
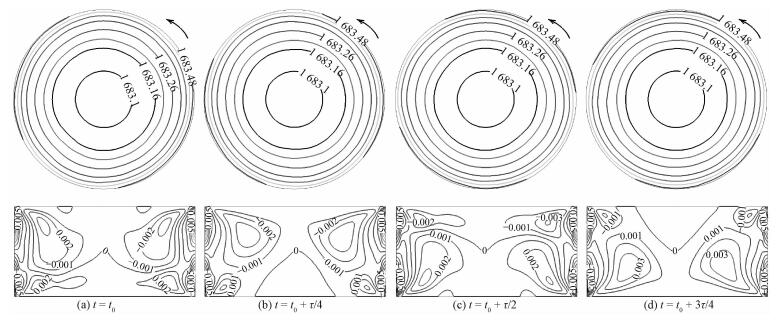
| 图 7 Ma=32.9时z=4 mm截面上的温度和θ=0切面上的轴向速度在一个振荡周期(τ=3.5 s)内的演化过程(1 mT, 50 Hz) Fig. 7 Temperature isolines at z=4 mm (up) and axial velocity isolines at θ=0(down) in one period (τ=3.5 s) under 1 mT RMF for Ma =32.9 | |
|
Download:
|
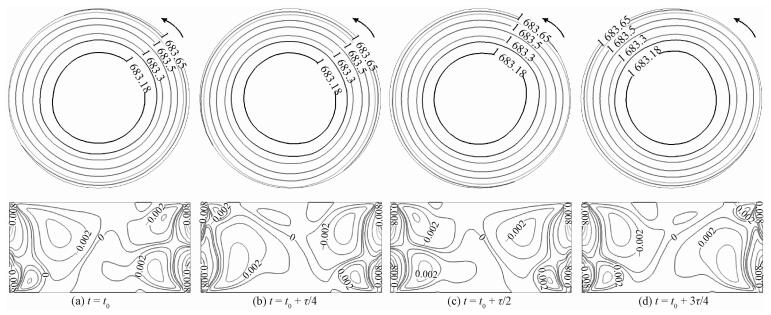
| 图 8 Ma=43.7时z=4 mm截面上的温度和θ=0切面上的轴向速度在一个振荡周期(τ=5.7 s)内的演化过程(1 mT, 50 Hz) Fig. 8 Temperature isolines at z=4 mm (up) and axial velocity isolines at θ =0(down) in one period (τ=5.7 s) under 1 mT RMF for Ma=43.7 | |
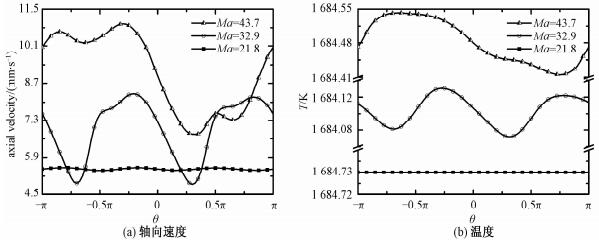
非稳态的对流热输运过程会引起温度场的波动,而温度场波动必定会影响单晶中的杂质分布,使得生长速率的波动与对流过程间接耦合起来,表现在浓度分布上就是杂质条纹,这对晶体生长极为不利。图 9给出z=2.5 mm时某一时刻自由表面上不同方位角的轴向速度和温度分布,其中图 9(a)为轴向速度分布,可以看出,3种情况下的轴向速度均有不同程度的波动,其中Ma=43.7和32.9的波动幅度远大于Ma=21.8时的波动幅度。受轴向速度波动的影响,Ma=43.7和32.9时自由表面环线上的温度也有较大的波动,而Ma=21.8时轴向速度波动较小,环线上的温度几乎不变,如图 9(b)所示。对比图 9(a)和9(b)发现:当Ma =32.9时,环线上轴向速度出现2个峰值和谷值,对应位置处的温度也出现峰值和谷值;当Ma =43.7时,环线上轴向速度在[-π, 0]区间的平均值比在[0, π]区间的大,对应位置处则分别为高温区和低温区;而Ma =21.8时,环线上轴向速度虽有3个峰值和谷值,但其幅值不足以使温度发生变化。
|
Download:
|
| 图 9 B0=1 mT时不同Ma数下z=0.25 mm截面上自由表面处环线上的轴向速度和温度分布 Fig. 9 Axial velocity (a) and temperature (b) on the circumference with r=10 mm at section z=2.5 mm under 1mT RMF for different Ma numbers | |
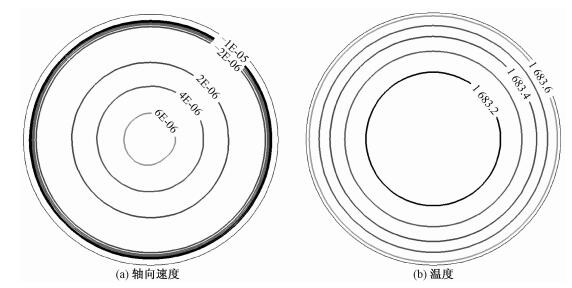
适当调节旋转磁场的磁场强度,可以使强迫对流成为熔体内的主导运动。对于Ma=21.8和Ma=32.9的熔体,分别施加2 mT和3 mT的旋转磁场,熔体内的三维振荡流转变为准二维的旋转轴对称流,从而实现在晶体生长过程中对传热传质较好的控制。对Ma=43.7的熔体,旋转磁场的强度需要进一步增加,数值结果表明,当磁场强度增加到B0=5 mT时,熔体中的温度及速度波动被有效抑制。Ma=43.7时,B0=5 mT作用下,图 10(a)显示中截面z=0上轴向速度等值线由一系列同心圆环构成,图 3中“蝌蚪”状的涡胞结构消失,其最大值在10-5 m/s量级,和提拉速度Vp在同一个数量级上;图 10(b)显示z=4 mm截面上温度亦呈中心对称分布。结合图 11中θ=0切面上的热毛细对流分布,不难得知熔区内对流关于中截面镜面对称。对Ma=21.8和32.9的熔体而言,当热毛细对流得到有效控制后,其结构与图 10和图 11中Ma=43.7时的流动结构相同,仅各物理量数值不同而已,不再一一列出。
|
Download:
|
| 图 10 B0=5 mT时Ma=43.7下z=0截面上轴向速度等值线和z=4 mm截面上温度等值线 Fig. 10 Axial velocity isolines at z=0 (a) and temperature isolines at z=4 mm (b) under 5 mT RMF for Ma =43.7 | |

|
Download:
|
| 图 11 B0=5 mT时Ma=43.7下θ=0切面上的热毛细对流分布 Fig. 11 Streamline distribution at θ =0 under 5 mT RMF for Ma=43.7 | |
如前所述,施加旋转磁场,不但对熔体周向产生搅拌作用,而且对轴向流动也具有抑制作用。有一点需要说明:不可以无限制地增加磁场强度来抑制轴向对流。以Ma=32.9为例,当磁场强度从1 mT增加到3 mT时,熔体轴向速度减小,然而,当磁场强度继续增大到5 mT时,轴向速度又重新上升到1 mT时轴向速度的水平。另一方面,磁场强度增加,熔体周向速度也越来越大,这对晶体生长界面和熔体自由表面都会产生不确定影响。杨光等[13]进行的激光熔凝钛合金的试验表明,未加磁场时熔池呈规则的圆形分布,施加80 mT,5 Hz的旋转磁场后熔池边缘形状反而变得不规则,并且沿熔池流动方向有细微的波纹状纹理。刘婵等[14]根据线性稳定性理论分析后发现,磁场强度增加时,导电流体中有2种不稳定模态依次起主导作用。电磁场的耦合作用不仅会使液态金属失稳,还会从自由表面生发出大量的二次液块甚至细小的液滴[15]。
4 结论本文采用全浮区模型,三维数值研究旋转磁场作用下熔区内热毛细对流的流动特性,分析辐射加热温度对流场的影响。研究结果表明:
1) 1 mT的均匀旋转磁场作用下,旋转磁场强度不足以有效地控制熔体的三维流动。本文3种不同辐射温度下的熔体对流均为周期性旋转振荡对流,周向波数分别为m=3、2、1;振荡频率随辐射温度的增加而减小,振荡主频分别为0.40、0.29和0.18 Hz。随着Ma数的增加,表面张力流随之增加,熔体周向最大速度和轴向最大速度近似为线性增长。当Ma数较小时,温度场主要由扩散作用决定,呈二维轴对称分布;随着Ma数的增加,熔体中的温度场受对流影响,亦呈周期性振荡,且振荡主频与对流振荡主频相同。
2) 保持旋转磁场的频率不变,增加磁场强度,可以使强迫对流成为熔体内的主导运动,熔体内的三维振荡流将转变为准二维的旋转轴对称流,熔体中的温度及速度波动被有效抑制。对于Ma=21.8和Ma =32.9的熔体,分别施加2 mT和3 mT的旋转磁场可以满足要求;对Ma=43.7的熔体,当磁场强度增加到B0=5 mT时,熔体中的传热传质得到有效控制。
| [1] |
Chang C E, Wilcox W R. Analysis of surface tension driven flow in floating zone melting[J]. International Journal of Heat and Mass Transfer, 1976, 19(4):355–366.
DOI:10.1016/0017-9310(76)90091-0 |
| [2] |
Levenstam M, Amberg G. Hydrodynamical instabilities of thermocapillary flow in a half-zone[J]. Journal of Fluid Mechanics, 1995, 297:357–372.
DOI:10.1017/S0022112095003132 |
| [3] |
Bazzi H, Nguyen C T, Galanis N. Numerical study of the unstable thermocapillary flow in a silicon float zone under μ-g condition[J]. International Journal of Thermal Sciences, 2001, 40:702–716.
DOI:10.1016/S1290-0729(01)01259-5 |
| [4] |
张银, 黄护林, 张喜东, 等. 微重力下温差对液桥自由界面变形的影响[J]. 工程热物理学报, 2015, 36(5):1091–1095.
|
| [5] |
Huang H, Zhu G, Zhang Y. Effect of Marangoni number on thermocapillary convection in a liquid bridge under microgravity[J]. International Journal of Thermal Sciences, 2017, 118:226–235.
DOI:10.1016/j.ijthermalsci.2017.05.003 |
| [6] |
Grants I, Gerbeth G. The suppression of temperature fluctuations by a rotating magnetic field in a high aspect ratio Czochralski configuration[J]. Journal of Crystal Growth, 2007, 308:290–296.
DOI:10.1016/j.jcrysgro.2007.09.002 |
| [7] |
Yildiz E, Dost S. A numerical simulation study for the combined effect of static and rotating magnetic fields in liquid phase diffusion growth of SiGe[J]. Journal of Crystal Growth, 2007, 303:279–283.
DOI:10.1016/j.jcrysgro.2006.11.196 |
| [8] |
Wang L, Shen J, Shang Z, et al. Preparation of gradient material in Sn-Cd peritectic alloy using rotating magnetic field[J]. Journal of Crystal Growth, 2013, 375:32–38.
DOI:10.1016/j.jcrysgro.2013.04.008 |
| [9] |
Dold P, Cröll A, Lichtensteige M, et al. Floating zone growth of silicon in magnetic fields:Ⅳ. Rotating magnetic fields[J]. Journal of Crystal Growth, 2001, 231:95–106.
DOI:10.1016/S0022-0248(01)01491-9 |
| [10] |
Yao L, Zeng Z, Li X, et al. Effects of rotating magnetic fields on thermocapillary flow in a floating half-zone[J]. Journal of Crystal Growth, 2011, 316:177–184.
DOI:10.1016/j.jcrysgro.2010.12.065 |
| [11] |
Li K, Hu W R. Effect of non-uniform magnetic field on crystal growth by floating-zone method in microgravity[J]. Science in China (Series A), 2001, 44(8):1056–1063.
DOI:10.1007/BF02878981 |
| [12] |
Rakoczy R. Enhancement of solid dissolution process under the influence of rotating magnetic field[J]. Chemical Engineering and Processing:Process Intensification, 2010, 49(1):42–50.
DOI:10.1016/j.cep.2009.11.004 |
| [13] |
杨光, 薛雄, 钦兰云, 等. 旋转磁场对激光熔凝钛合金熔池的影响[J]. 稀有金属材料与工程, 2016, 45(7):1804–1810.
|
| [14] |
刘婵, 张年梅, 倪明玖. 侧壁非对称的方管MHD流动的线性稳定性分析[J]. 中国科学院大学学报, 2016, 33(1):42–49.
|
| [15] |
王进进, 张杰, 倪明玖. 均匀磁场中初始静止的液态金属在电流作用下三维运动的数值研究[J]. 中国科学院大学学报, 2015, 32(2):166–171.
|
 2018, Vol. 35
2018, Vol. 35 


