随着现代工业的发展,能源正在迅速地枯竭。研究表明,相变材料可以有效地缓解太阳能的间歇性和不稳定性问题,有效实现能量的高效、合理利用,从而解决能源与环境问题[1-2]。
相变储热材料[3]主要包括:无机相变材料、有机相变材料和复合相变材料。复合相变材料[4]既能有效克服单一的无机物或有机物相变储热材料存在的缺点,又可以改善相变材料的应用效果以及拓展其应用范围。Giro-Paloma等[5]将石蜡和棕榈酸与基体聚苯乙烯封装成微胶囊,该相变材料具有良好的潜在能量储存性能。Alkan和Sari[6]将脂肪酸组装进聚甲基丙烯酸甲酯(PMMA),制备一系列脂肪酸/PMMA共混物,脂肪酸与PMMA间的相互吸引作用使得二者很好地相容。Zhong等[7]将膨胀石墨和二元熔融盐(LiNO3-KCl、LiNO3-NaNO3和LiNO3-NaCl)通过溶液浸渍法合成3种多孔异质复合相变材料,其导热系数比二元熔融盐提高4.9~6.9倍,该复合相变材料具有很好的热稳定性。
但上述的传统复合相变材料容易发生泄漏,需要封装,使用不安全,导热系数很低,不利于换热。当相变材料的尺寸达到纳米级别时,可极大地强化流体的传热性能,减少磨损破裂、堵塞管道等现象。利用纳米技术制备复合相变材料,能够解决泄漏问题,同时提高其导热系数,在一定程度上可以克服普通相变蓄能材料的诸多缺点[8-9]。例如:Yang等[10]制备的聚乙二醇/二氧化硅定形相变复合材料,二氧化硅的结构可以强烈阻碍PEG的结晶;Zhang等[11]通过物理的方法制备一系列的定形相变材料,由聚乙二醇醚(Brij76)和介孔二氧化硅(MCM-41)组成。纳米孔复合相变材料[12]已成为研究相变储能的热点。随着纳米材料的发展和相变储能重要性的日益提升,已成功将金属纳米颗粒组装制备成复合相变材料,显著改善了相变材料的性能[13]。将高导热的金属纳米颗粒填充到基材中,可得到具有较高有效导热系数的复合相变材料。同时,将纳米技术应用于相变材料领域,使相变材料的聚集形态发生改变后,能够提高其储能效率、减少能量传输的单次循环时间、增加相变材料的寿命,拓展其工作的范围和温度区间。
目前对金属纳米颗粒复合相变材料的相变热特性的研究尚不成熟,研究金属纳米颗粒复合相变材料的相变热特性不仅有利于深入了解热物理机制,掌握材料本身的热物理性质,而且对通过结构设计复合相变材料具有重要意义。本文针对由纳米颗粒和纳米孔基材组装成的纳米复合相变材料,主要采用分子动力学模拟,研究金属纳米颗粒的相变行为及热特性,并选择典型纳米孔基材(MCM-41)开展热特性的研究,进一步考虑复合材料的相变热特性,尤其是纳米颗粒的引入对基材相变热特性的影响。
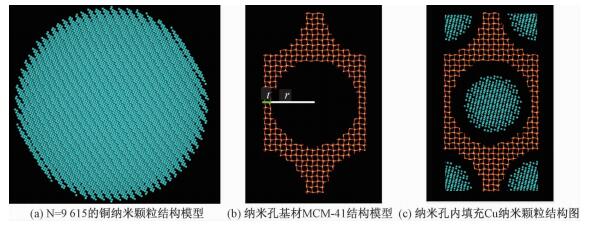
1 计算模型及方法 1.1 结构模型对于纳米孔基材,本文选取纳米孔二氧化硅(MCM-41),其孔道(孔径1.6~10 nm[12])高度有序,具有六方截面结构和一维线性特征,呈规则阵列排列,且孔径在纳米范围可调。MCM-41是纳米粒子组装的理想宿主,它可以导入各种纳米颗粒/团簇,例如Cu纳米颗粒[14]、Ag纳米线[15]、碳纳米管[16]等等。填充铜纳米颗粒的MCM-41的结构如图 1所示。铜纳米颗粒一般由几个到几百个甚至成千上万个原子构成,直径在1~100 nm不等,纳米颗粒的直径为d。假设纳米颗粒在孔道内沿轴向方向呈直线分布,颗粒与颗粒间相接触,且纳米颗粒与孔道壁面间存在着受限空气。图中t为壳壁半壁厚,r为孔道半径。
|
Download:
|
| 图 1 纳米孔复合材料Cu/MCM-41结构图 Fig. 1 Nanostructures of Cu/MCM-41 nanoporous composite | |
对应的纳米孔二氧化硅基材的结构尺寸,如表 1所示。
|
|
表 1 SiO2基材模拟工况 Table 1 Simulation condition of SiO2 substrate |
鉴于微观实验的高难度,目前纳米材料的相变行为研究主要采用理论分析和分子动力学模拟(MD)[17-19]。现有的不少研究都揭示了纳米材料热物性的尺度效应。本文针对小尺寸的金属纳米颗粒,对其热特性开展分子动力学模拟与分析。
1.2.1 势函数对于单独金属纳米铜颗粒,本文采用EAM势函数模型,它是能够很好地处理金属相变的热力学性质的多体势能模型,其表达式为
| $ {E_i} = \sum\limits_i {{F_i}\left( {{\rho _{ij}}} \right) + \frac{1}{2}\sum\limits_{i \ne j} {{\mathit{\Phi }_{ij}}} \left( {{r_{ij}}} \right).} $ | (1) |
式中:Ei是总内能;Fi(ρij)是原子i嵌入时产生的嵌入能,ρij是由除原子i外的所有原子在原子i处产生的电子密度,Φij(rij)是原子i和原子j之间的势能,rij是原子i和原子j之间的距离。
对于纳米孔二氧化硅基材,本文采用Tersoff势函数,它能很好地描述Si-O原子间的相互作用势,表达式为
| $ \begin{array}{l} {E_i} = \sum\limits_i {{E_{ij}} = \frac{1}{2}\sum\limits_{i \ne j} {{\mathit{V}_{ij}}} } \\ = \frac{1}{2}\sum\limits_{i \ne j} {{f_{\rm{C}}}\left( {{r_{ij}}} \right)\left[{{a_{ij}}{f_{\rm{R}}}\left( {{r_{ij}}} \right) + {b_{ij}}{f_{\rm{A}}}\left( {{r_{ij}}} \right)} \right].} \end{array} $ | (2) |
式中:Ei为i原子的位势;Eij是i,j原子间的交互作用能;fR和fA分别表示排斥和吸引作用;fC是光滑截断函数。
对于纳米孔复合材料(Cu/MCM-41),其结构中存在3种作用力,与纳米铜颗粒内部强作用力和SiO2基材内部强作用力相比,Cu与SiO2之间的范德瓦尔斯力要弱很多,因此使用LJ(Lennard-Jones)势函数模型描述,如下:
| $ E\left( r \right) = 4\varepsilon \left[{{{\left( {\frac{\sigma }{r}} \right)}^{12}}-{{\left( {\frac{\sigma }{r}} \right)}^6}} \right]. $ | (3) |
式中:ε是LJ势阱参数,r为原子间距离,σ为LJ平衡常数。
1.2.2 模拟过程分子动力学模拟过程主要依靠lammps分子动力学模拟软件(简称lammps)实现,得到纳米材料的初始结构之后,为使其结构更稳定且趋于真实结构,对其进行退火处理。在自由边界条件的正则系综(NVT)下,完成退火之后得到的基态结构,设置每一个原子的初速度按麦克斯韦(Maxwell)分布随机给定,进一步实现升温过程。
1.2.3 相变点与热容计算方法结合热容温度曲线来确定颗粒的熔点和凝固点,根据维里定理,系统的平均动能和系统的平均势能存在线性相关关系。又按照能量均分定理,系统的平均动能又与温度呈线性相关,所以平均势能与温度呈线性相关。所以对于铜纳米颗粒的计算可以根据势能的突变来确定熔点的位置。由于二氧化硅基材和复合材料为非晶体,没有固定的熔点,因此求解原子均方根位移来确定其熔化区。均方根位移表达式为
| $ {\rm{MSD}} = \left\langle {{{\left| {r\left( t \right)-r\left( 0 \right)} \right|}^2}} \right\rangle . $ | (4) |
对于热容的计算,则是通过内能对温度的倒数求得热容:
| $ {C_{\rm{V}}} = \frac{{{\rm{d}}E\left( T \right)}}{{{\rm{d}}T}}. $ | (5) |
本文采用分子动力学模拟铜纳米颗粒,其熔点和比热容如图 2、图 3所示。

|
Download:
|
| 图 2 铜纳米颗粒的熔点随尺寸的变化 Fig. 2 Variation in melting point of Cu nanoparticles with size | |
|
Download:
|
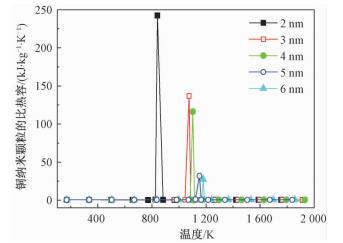
| 图 3 铜纳米颗粒的比热容随温度和尺寸的变化 Fig. 3 Variation in heat capacity of Cu nanoparticles with temperature and size | |
图 2是铜纳米颗粒熔点随颗粒尺寸变化的曲线,可以看出,不同尺寸纳米颗粒的熔点均低于铜块体的熔凝点(1 357.77 K);且随着原子数的减少,纳米颗粒的熔点也相应降低。这个结果充分体现了纳米颗粒熔点的尺寸效应,即熔点随纳米颗粒尺寸的减小而降低,纳米颗粒熔化所需要增加的内能比块材熔化所需的能量小得多,与前人所做的研究工作结论相一致。产生这种现象的原因是由于表面原子具有的表面能与颗粒的总能量比例的变化。球形颗粒比表面积(表面积/体积)与直径成反比,颗粒直径越小导致表面原子数占总原子数的比重增大,表面能也相应增加,表面原子配位不足极易与其他原子结合,结构不稳定,故而导致纳米颗粒的熔点比块材低,而且直径越小熔点越低。
图 3表示不同尺寸(不同原子数)的铜纳米颗粒比热容与温度的关系,铜块材的比热容为0.39 kJ/(kg·K),可以看出,铜纳米颗粒熔化前后的比热容大大高于块材的比热容值,这是由于纳米结构材料表面原子多,没有像内部原子一样的规则排列,原子间约束力较小,所以比热容也比块材的大,这样也更有利于提高材料的储能性质。
2.2 纳米孔基材的热特性在加热过程中,基材没有明确的熔点,而是一段熔化区,通过分析SiO2熔化过程中温度与内能关系,确定各工况下SiO2的熔化区,如表 2所示。这是因为基材二氧化硅为非晶体,由于分子的排列不规则,吸收热量后不需要破坏分子的有规则排列,只用来提高平均动能,所以当从外界吸收热量时,温度不断升高,并由硬变软,最后变成液体,故而基材没有明确的熔点,但是其熔化区的温度也会随基材尺寸大小的增加而变高。
|
|
表 2 SiO2孔半径和熔化区关系 Table 2 Relationship between pore radius and melting zone of SiO2 |
SiO2基材的比热容如图 4,查得T=300 K时SiO2块材的比热容为0.745 kJ/(kg·K),而由图可以看出各个工况下SiO2基材比热容明显比块材的小。从图中可知基材比热容随温度的升高有上升趋势,固液转化前后也大致呈现出液态比热容较高的现象,且随着孔径的增加,基材的比热容逐渐增大。

|
Download:
|
| 图 4 纳米孔基材MCM-41比热容随着孔半径的变化 Fig. 4 Variation in heat capacity of nanoporous substrate(MCM-41) with radius | |
图 5为粒径为2 nm铜纳米颗粒填充到孔半径为1.49 nm的SiO2基材中组成的纳米孔复合材料的温度-均方根位移图。可以看出,复合材料为固态时温度-均方位移关系接近y=0.054 9,变为液体后为y=5×10-5x-0.018 2,2条线交点处的温度值即为复合材料熔点,为1 462 K,高于Cu纳米颗粒的熔点868.5 K和基材的熔化区760~1 150 K,说明SiO2-Cu体系为增强作用。鉴于此,填充物结构稳定性增强,导致熔点升高。

|
Download:
|
| 图 5 纳米孔复合材料均方根位移随温度的变化 Fig. 5 Variation in MSD of nanoporous composite with temperature | |
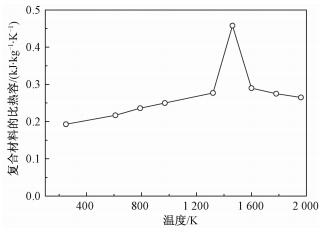
进一步考察复合材料的比热,结果如图 6所示。可以看出,复合材料的比热容介于二氧化硅基材与Cu纳米颗粒之间,说明填充Cu纳米颗粒后能有效地改善纳米孔基材的储热特性。同时,比热容在熔点处存在峰值,其趋势与Cu纳米颗粒一致。
|
Download:
|
| 图 6 纳米孔复合材料(Cu/MCM-41)的比热容随温度的变化 Fig. 6 Variation in heat capacity of nanoporous composite (Cu/MCM-41) with temperature | |
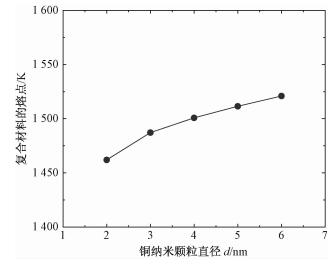
最后考察填充铜纳米颗粒尺寸对复合相变材料热特性的影响,结果如图 7所示。可以看出,复合材料熔点均高于Cu纳米颗粒和基材的熔点,且随着Cu纳米颗粒尺寸的增加,复合材料的熔点逐渐升高。
|
Download:
|
| 图 7 纳米孔复合材料(Cu/MCM-41)的熔点随颗粒尺寸的变化 Fig. 7 Variation in melting point of nanoporous composite (Cu/MCM-41) with size of Cu nanoparticle | |
本文分别对Cu纳米颗粒、SiO2纳米孔基材以及他们的复合材料的熔点、比热进行研究,结论如下:
1) Cu纳米颗粒的相变点显著低于块体材料,且随尺度增加而增加,但最终会趋于块体相变点;纳米尺度下Cu原子混乱度增加,导致熵增,因此纳米材料比热要高于同类块材;随着粒径的减小,纳米颗粒表面原子比例升高,表面能大幅度增加,熔化时需要增加的内能就要小得多。
2) 基材二氧化硅为非晶体,没有明确的熔点,熔化时温度持续上升,其熔化区呈现出随尺寸增大升高的趋势;各工况下比热值比相同条件下块体材料值明显偏小,且比热容随其孔径增大和温度升高而增大。
3) SiO2-Cu体系为增强作用,且由于基材孔径与Cu颗粒间隙强化了增强作用,复合材料熔点高于Cu颗粒和纳米孔基材的熔点,
| [1] |
Xiao X, Zhang P, Li M. Thermal characterization of nitrates and nitrates/expanded graphite mixture phase change materials for solar energy storage[J]. Energ Convers Manage, 2013, 73(73):86–94.
|
| [2] |
Singh S P, Vijay B. Applications of organic phase change materials for thermal comfort in buildings[J]. Rev Chem Eng, 2014, 30(5):521–538.
|
| [3] |
Sarier N, Onder E. Organic phase change materials and their textile applications:an overview[J]. Thermochimica Acta, 2012, 540(1):7–60.
|
| [4] |
冷光辉, 蓝志鹏, 葛志伟, 等. 储热材料研究进展[J]. 储能科学与技术, 2015, 4(2):119–130.
|
| [5] |
Giro-Paloma J, Konuklu Y, Fernández A I. Preparation and exhaustive characterization of paraffin or palmitic acid microcapsules as novel phase change material[J]. Sol Energy, 2015, 112(112):300–309.
|
| [6] |
Alkan C, Sari A. Fatty acid/poly (methyl methacrylate) (PMMA) blends as form-stable phase change materials for latent heat thermal energy storage[J]. Sol Energy, 2008, 82(2):118–124.
DOI:10.1016/j.solener.2007.07.001 |
| [7] |
Zhong L, Zhang X, Luan Y, et al. Preparation and thermal properties of porous heterogeneous composite phase change materials based on molten salts/expanded graphite[J]. Sol Energy, 2014, 107(9):63–73.
|
| [8] |
Song Q, Li Y, Xing J, et al. Thermal stability of composite phase change material microcapsules incorporated with silver nano-particles[J]. Polymer, 2007, 48(11):3317–3323.
DOI:10.1016/j.polymer.2007.03.045 |
| [9] |
Johnston J H, Grindrod J E, Dodds M, et al. Composite nano structured calcium silicate phase change materials for thermal buffering in food packaging[J]. Curr Appl Phys, 2008, 8(3/4):508–511.
|
| [10] |
Yang H, Feng L, Wang C, et al. Confinement effect of SiO2 framework on phase change of PEG in shape-stabilized PEG/SiO2composites[J]. Eur Polym J, 2012, 48(4):803–810.
DOI:10.1016/j.eurpolymj.2012.01.016 |
| [11] |
Zhang L, Shi H, Li W, et al. Structure and thermal performance of poly(ethylene glycol) alkyl ether (Brij)/porous silica (MCM-41) composites as shape-stabilized phase change materials[J]. Thermochim Acta, 2013, 570(9):1–7.
|
| [12] |
Huang X, Dong W, Wang G, et al. Synthesis of confined Ag nanowires within mesoporous silica via double solvent technique and their catalytic properties[J]. J Colloid Interf Sci, 2011, 359(1):40–46.
DOI:10.1016/j.jcis.2011.03.049 |
| [13] |
Zhou Y, Wang Y, Zhang J H, et al. Hot probe method for measuring thermal conductivity of copper nano-particles/paraffin composite phase change materials[J]. Key Engineering Materials, 2013, 561:428–434.
DOI:10.4028/www.scientific.net/KEM.561 |
| [14] |
Bischof C, Hartmann M. Synthesis and characterization of ruthenium-containing MCM-41 and MCM-48 mesoporous materials[C]//Treacy M M J, Marcus B K, Bisher M E, et al. Proceedings of the 12th International Zeolite Conference. Warrendale, PA: Materials Research Society, 1999: 809-816.
|
| [15] |
Adhyapak P V, Karandikar P, Vijayamohanan K, et al. Syhthesis of Silver Nanowires inside Mesoporous MCM-41 Host[J]. Mater Lett, 2004, 58(58):1168–1171.
|
| [16] |
Ciuparu D, Chen Y, Lim S, et al. Uniform-diameter single-walled carbon nanotubes catalytically grown in cobalt-incorporated MCM-41[J]. J Phys Chem B, 2004, 108(2):503–507.
DOI:10.1021/jp036453i |
| [17] |
Lai S L, Carlsson J R A, Allen L H. Melting point depression of Al clusters generated during the early stages of film growth:nanocalorimetry measurements[J]. Appl phys Lett, 1998, 72(9):1098–1100.
DOI:10.1063/1.120946 |
| [18] |
Sun J, Simon S L. The melting behavior of aluminum nanoparticles[J]. Thermochim Acta, 2007, 463(1):32–40.
|
| [19] |
Alavi S, Thompson D L. Molecular dynamics simulations of the melting of aluminum nanoparticles[J]. J Phys Chem A, 2006, 110(4):1518–1523.
DOI:10.1021/jp053318s |
 2018, Vol. 35
2018, Vol. 35 


