2. 西安交通大学热流科学与工程教育部重点实验室, 西安 710049
2. Key Laboratory of Thermo-Fluid Science and Engineering of Ministry of Education, Xi'an Jiaotong University, Xi'an 710049, China
纵向涡强化技术是基于纵向涡旋在流场中的流动特性来实现强化传热的目的,纵向涡一般依靠纵向涡发生器(longitudinal vortex generator,LVG)来产生。Torri等[1]将纵向涡发生器的布置方式分为渐扩式(common-flow-down,CFD)和渐缩式(common-flow-up,CFU)。作为第3代强化传热表面的代表形式,纵向涡发生器得到很多学者的关注。王令等[2]和Wang等[3]实验研究矩形通道内安装CFD式纵向涡发生器的流动换热性能,结果表明,CFD式纵向涡发生器能够增强矩形通道内流动工质的换热性能,但是阻力损失增大更多。Chen等[4]对微通道内安装的CFD式纵向涡发生器的流动换热性能进行实验研究,结果表明,换热性能比光通道增加12.3%~73.8%,但阻力性能增加幅度更大,为40.3%~158.6%。Ebrahimi等[5]对微通道内安装CFD式纵向涡发生器的流动换热性能进行数值计算研究,Re范围为100~1 100,结果表明,换热性能比光通道增加2.0%~25.0%,阻力性能增加4.0%~30.0%。上述研究结果表明,CFD式纵向涡发生器的阻力损失增加幅度大于换热性能的增加幅度,其综合流动换热性能的优势并不一定能够得到体现。对于CFU式纵向涡发生器,与平直翅片或者光通道相比,增加相同换热性能的同时,其阻力损失增加较少,甚至降低,能够表现出优良的综合流动换热性能,近年来也受到很多学者的关注。何雅玲等[6]对CFU式纵向涡发生器翅片管翅式换热器流动换热性能进行研究,计算结果表明,当纵向涡发生器攻角为15°,采用3对矩形翼时,管翅式换热器的空气侧换热能力的提升幅度超过流动阻力增加的幅度。Wu等[7]对CFU式纵向涡发生器的流动换热性能进行实验研究,研究结果表明,CFU式纵向涡发生器的Nu比平直翅片增大16.5%,而流动阻力损失却几乎不变。张强和王良璧[8]对通道内CFU式矩形涡发生器强化换热性能进行数值研究,结果发现,随雷诺数的增加换热性能增强;随涡发生器高度增大换热性能增强,但阻力系数会急剧增加;当攻角为29°时,强化换热效果最好。Tang等[9]对CFD和CFU两种形式纵向涡发生器翅片管翅式换热器的流动换热性能进行计算比较,发现CFU式纵向涡发生器Nu比CFD式纵向涡发生器在计算范围内平均增大2.8%,f因子却平均减少9.1%。Tian等[10]对布置CFD和CFU两种形式纵向涡发生器的矩形通道内流动换热性能进行比较研究,结果表明CFU式纵向涡发生器的换热性能优于CFD式纵向涡发生器。唐凌虹等[11]数值研究矩形通道内布置CFD和CFU两种形式矩形翼纵向涡发生器的流动换热性能,结果表明,CFU式纵向涡发生器与椭圆支柱共同作用下矩形通道内的综合流动换热性能最优。以上研究成果表明CFU式纵向涡发生器能够强化传热性能,本文在文献[11]研究基础上,对不同形状纵向涡发生器的流动换热性能进行比较研究,期望得到矩形通道内综合流动换热性能更好的纵向涡发生器形式,为相应的工程设计提供参考。
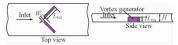
1 物理模型及计算方法图 1为矩形通道内布置纵向涡发生器的结构示意图,工作流体为水。图 1中,L1为通道进口段长度,值为100 mm;L2为电加热段,值为450 mm;L3为通道出口段,值为50 mm;L4为纵向涡发生器的安装位置,值为60 mm;W为矩形通道宽度,值为40 mm;H为矩形通道高度,值为3 mm;Pl为纵向涡发生器纵向间距,值为100 mm。

|
Download:
|
| 图 1 几何模型示意图 Fig. 1 Schematic of the physical model | |
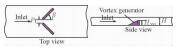
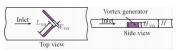
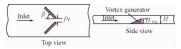
本文研究的矩形通道内纵向涡发生器结构形式和布置方式具体描述如表 1所示,图 2为Case F结构示意图。
|
|
表 1 不同矩形通道计算模型 Table 1 List of channel configurations |

|
Download:
|
| 图 2 Case F结构示意图 Fig. 2 Schematic of Case F | |
表 2列出计算模型具体的其他几何参数。
|
|
表 2 计算模型其他几何参数 Table 2 Geometric dimension of various vortex generators |
流动与换热控制方程的通用形式为
| $ \nabla \cdot \left( {\rho \mathit{\boldsymbol{V}}\phi } \right) = \nabla \cdot \left( {{\mathit{\Gamma }_\phi }\nabla \phi } \right) + {S_\phi }, $ | (1) |
变量ϕ的扩散系数Γϕ的具体形式如表 3所示。
|
|
表 3 变量ϕ的扩散系数Γϕ Table 3 Expressions for ϕ and Γϕ |
湍流模型采用SST k-ω湍流模型,在近壁处应用k-ω模型,在边界层边缘和自由剪切层应用k-ε模型,其间用一个混合函数来过渡,其湍流动能k方程和比耗散率ω方程表达方式如下所示:
| $ \begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}k} \right)}}{{\partial {x_j}}} = P- {\beta ^*}\rho \omega k + \hfill \\ \;\;\;\;\;\;\;\;\frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + {\sigma _{\rm{k}}}{\mu _{\rm{t}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right], \hfill \\ \end{gathered} $ | (2) |
| $ \begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\omega } \right)}}{{\partial {x_j}}} = \frac{{\gamma \rho }}{{{\mu _{\rm{t}}}}}P- \beta \rho {\omega ^2} + \hfill \\ \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + {\sigma _\omega }{\mu _{\rm{t}}}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right] + 2\left( {1 -{F_1}} \right)\frac{{\rho {\sigma _\omega }}}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}}, \hfill \\ \end{gathered} $ | (3) |
式中:P为压力项;ρ为密度;xj为坐标向量;F1、β、γ、σk和σω均为模型参数;β*为模型常数,取为0.09。
数值计算采用Fluent软件,采用SIMPLEC算法处理速度和压力耦合问题,对流项采用QUICK格式进行离散,扩散项采用中心差分格式(CD)。计算模型网格划分应用Gambit软件生成结构化网格,在纵向涡发生器周围进行了局部加密。
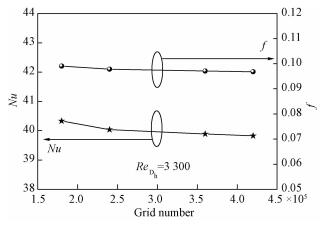
在进行计算之前,先对Case A进行网格无关性考核,如图 3所示。图 3中,网格数为2.4×105的计算模型与网格数为3.6×105的Nu数和f因子分别相差0.4%和0.8%,网格数为3.6×105的计算模型与网格数为4.2×105的Nu数和f因子分别相差0.2%和0.3%,所以本文采用网格数量为3.6×105的网格进行计算。
|
Download:
|
| 图 3 网格无关性考核 Fig. 3 Variation of grid independence | |
计算区域的各边界条件为:进口边界速度为u=u0、v=w=0,温度为300 K;出口边界假定流体流动与换热均达到充分发展;矩形通道布置纵向涡发生器的表面为常热流边界条件,q=const,其余3个侧面均为绝热边界条件。
Reynolds数定义为
| $ R{e_{{D_{\rm{h}}}}} = \frac{{{u_0}{D_{\rm{h}}}}}{\nu }, $ | (4) |
Nusselt数定义如下
| $ Nu = \frac{{h{D_{\rm{h}}}}}{\lambda }, $ | (5) |
j因子定义如下
| $ j = \frac{{Nu}}{{R{e_{{D_{\rm{h}}}}}P{r^{1/3}}}}, $ | (6) |
阻力系数f定义如下
| $ f = \frac{{\Delta p}}{{\left( {0.5\rho {u_0}^2L/{D_{\rm{h}}}} \right)}}. $ | (7) |
上述公式中,Dh为通道的当量直径,Dh=4A/P,A为矩形通道的流通面积,P为湿周的周长;h为平均对流换热系数,h=q/(tw-tf),tw为加热面的平均壁面温度,tf=(tin+tout)/2,tin、tout分别为矩形通道进、出口水的温度;ν为运动黏度;λ为导热系数;Pr为Prandtl数;ρ为密度;L为流动方向总长度;Δp为矩形通道的流动阻力。
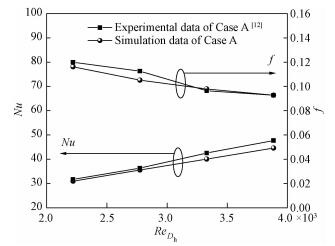
2 计算模型考核在对矩形通道物理模型进行数值计算之前,本文计算Case A和光通道的流动换热性能,并与实验数据进行比较,如图 4和图 5所示。Case A的实验数据来自于文献[12],光通道换热性能关联式采用Dittus-Boelter公式[13]、阻力性能关联式采用Blasius公式[14],如下所示:
|
Download:
|
| 图 4 Case A计算值与实验值对比 Fig. 4 Nu and f-factor comparisons for Case A | |

|
Download:
|
| 图 5 光通道计算值与实验值对比 Fig. 5 Nu and f-factor comparisons for smooth channel | |
| $ Nu = 0.023Re_{{D_{\rm{h}}}}^{0.8}P{r^{0.4}}, $ | (8) |
| $ f = \frac{{0.316}}{{Re_{{D_{\rm{h}}}}^{0.25}}}. $ | (9) |
由图 4和图 5可知,Case A和光通道的Nu计算值和实验值的平均偏差分别为4.2%和4.8%;f因子的平均偏差分别为2.1%和3.7%,可以认为布置纵向涡发生器矩形通道的计算模型是可靠的。
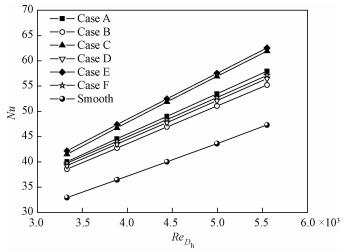
3 不同形式涡发生器流动传热性能比较 3.1 涡发生器换热性能比较图 6为矩形通道内不同结构形式和布置方式涡发生器流动换热性能比较。由图 6可知,与光通道相比,随着水的Re的增大,纵向涡发生器均使矩形通道内换热性能得到增强;在相同Re下,Case E的Nu最大,Case C次之,接下来依次是Case A、Case F、Case D和Case B,光通道的Nu最小。在Re计算范围内,Case A、Case C和Case E或者Case B、Case D和Case F的比较结果表明CFU式纵向涡发生器能够比CFD式纵向涡发生器提供更好的换热性能。对于三角形翼和矩形翼纵向涡发生器,矩形翼纵向涡发生器的换热性能均强于对应的三角形翼纵向涡发生器,这表明矩形翼对流体的扰动能力更强,扰动范围更广,使流体混合得更好,增强了对流换热性能。
|
Download:
|
| 图 6 不同矩形通道传热性能比较 Fig. 6 Nu comparison among channels | |
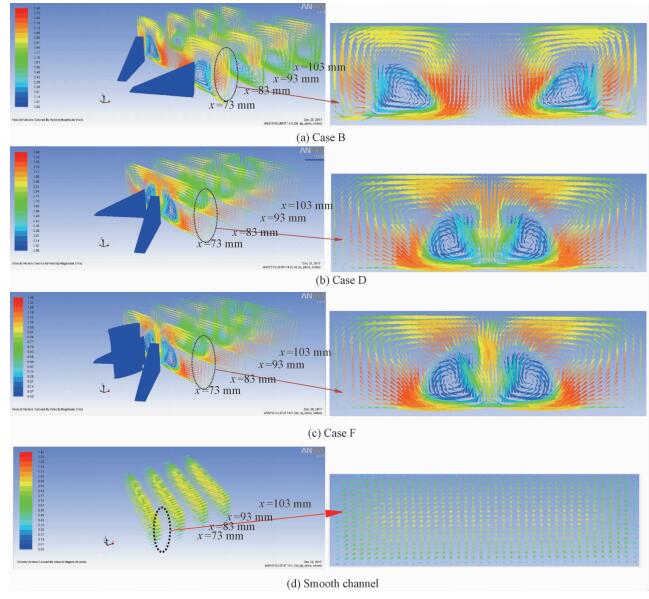
图 7给出Case B、Case D、Case F和光通道在流体入口速度为0.8 m/s时不同截面的速度分布。从图 7可以看出,当流体流经纵向涡发生器时,Case B、Case D和Case F均产生向相反方向旋转的纵向涡对。相邻纵向涡对的运动可以分为相同方向旋转和相反方向旋转两种方式,相反方向旋转纵向涡对指的是由涡发生器产生的二次流以相反方向旋转。Case B结构形式的三角形翼中间的边界层被破坏时,流体向通道下壁面方向旋转,与壁面的相互作用增强;而Case D和Case F结构形式的三角形翼中间边界层被破坏时,流体旋转方向刚好相反。尽管这两种形式涡发生器产生的漩涡旋转方向不同,但都能对流体产生强烈的扰动,导致边界层的破坏,从而使换热能力得到提高。
|
Download:
|
| 图 7 通道x方向不同截面速度分布(u0=0.8 m/s) Fig. 7 Velocity distributions at different cross-sections (u0=0.8 m/s) | |
场协同原理指出在一定的速度及温度梯度下要强化对流换热,实质上要减小速度和温度梯度之间的夹角,夹角越小,速度与温度梯度之间的协同越好,在其他条件相同时,换热性能就越好[15]。本文应用场协同原理对不同结构形式和布置方式涡发生器流动换热性能进行解释说明。协同角采用全场体积平均角来计算[16]:
| $ \mathit{\boldsymbol{U}} \cdot \nabla t = \left| {\vec U} \right| \cdot \left| {\nabla t} \right|\cos \theta $ | (10) |
| $ \theta = \arccos \left( {\frac{{\vec U \cdot \nabla t}}{{\left| {\vec U} \right| \cdot \left| {\nabla t} \right|}}} \right) $ | (11) |
| $ {\theta _{\rm{m}}} = \frac{{\iiint_V {\theta {\rm{d}}v}}}{{\iiint_V {{\rm{d}}v}}} $ | (12) |
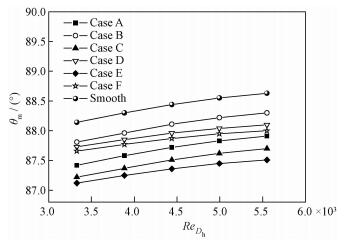
由图 8可知,随着通道内水Re的增加,不同矩形通道的全场体积平均协同角均随之增大。在整个Re计算范围内,Case E的全场体积平均协同角最小,Case C次之,接下来依次是Case A、Case F、Case D和Case B,光通道的全场体积平均协同角最大。对比图 6和图 8可知,相同Re下全场体积平均协同角较小的矩形通道对应的换热系数较大,这与场协同理论是完全一致的,也就是说,纵向涡发生器产生的二次流能够减小主流的速度和温度梯度的夹角,使通道内的换热性能得到强化。
|
Download:
|
| 图 8 不同形式纵向涡发生器全场体积平均协同角比较 Fig. 8 Volume average synergy angle θm comparison | |
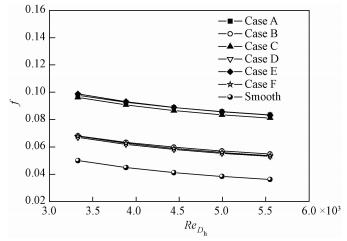
布置不同结构形式纵向涡发生器矩形通道内水的流动阻力性能随Re的变化如图 9所示。随着Re的增大,根据式(7)计算得到的各矩形通道阻力系数f因子减小。在相同的Re下,矩形翼涡发生器的f因子大于三角形翼涡发生器的f因子。Case C和Case D的f因子分别小于Case A和Case B的f因子,表明CFU式纵向涡发生器的阻力性能要优于CFD式纵向涡发生器。其原因可以解释如下:流体流经布置纵向涡发生器的矩形通道时,流动阻力损失包括沿程阻力损失和纵向涡发生器造成的阻力损失(形阻),并且纵向涡发生器造成的阻力损失在总阻力损失中占主导作用。这样,当流体流经纵向涡发生器时,由于CFD式纵向涡发生器形成的涡旋旋转特性,其对水流造成的形阻大于CFU式纵向涡发生器;同时由于CFU式纵向涡发生器形成的涡旋互相提升远离通道的下壁面,其形阻甚至会比光通道还小,因此,CFD式纵向涡发生器造成的阻力损失要大于CFU式纵向涡发生器的阻力损失。
|
Download:
|
| 图 9 不同矩形通道阻力性能比较 Fig. 9 Comparison of f-factor among channels | |
图 10给出Case B、Case D、Case F和光通道在流体速度为0.8 m/s时局部阻力损失的对比。从图 10可以看出,当水流到纵向涡发生器之前,矩形通道内的局部阻力损失几乎相同,但当水流过纵向涡发生器过程中,Case B的局部阻力损失大于Case D。比较Case D和Case F的局部阻力损失可知,Case F的局部阻力损失大于Case D,这是因为Case F结构是由Case D与椭圆支柱组合形成的,当水流经过Case F形式的纵向涡发生器时,额外的椭圆支柱造成水流湍流度的增加,导致流动阻力损失增大。
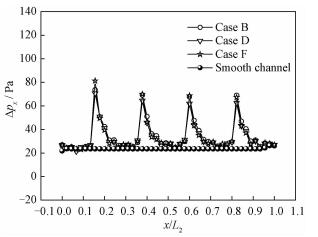
|
Download:
|
| 图 10 不同矩形通道局部阻力损失比较 Fig. 10 Local pressure drops for channels | |
从上述比较可知,换热性能的增加往往伴随着阻力损失的增大,因此,很有必要对不同矩形通道的综合流动换热性能进行比较。在对换热器综合流动换热性能进行评价时,常利用JF因子来评价强化传热性能的好坏,JF因子越大,表示综合性能越好。JF因子表达式[17]如下:
| $ JF = \frac{{j/{j_{{\rm{ref}}}}}}{{{{\left( {f/{f_{{\rm{ref}}}}} \right)}^{1/3}}}}, $ | (13) |
式中,下标“ref”表示光通道。
图 11给出各矩形通道JF因子随Re的变化情况。随着Re的增大,各矩形通道JF因子减小,这是因为,j因子和f因子随着Re的增大均减小;但是随着水流动速度(Re)的增加,流动扰动对换热性能的增强幅度小于阻力性能的增加幅度,即j因子减小的幅度大于f因子减小幅度,因此JF因子随Re增大而减小。从图 11可以清楚地看出,Case F的综合流动换热性能最好,Case D次之,接下来依次是Case B、Case E、Case C和光通道,Case A的综合流动换热性能最差。在研究的Re范围内,三角翼纵向涡发生器的JF因子均大于对应的矩形翼纵向涡发生器,这表明三角翼纵向涡发生器能够提供更好的综合流动换热性能。CFU式纵向涡发生器的JF因子大于对应的CFD式纵向涡发生器,表明CFU式纵向涡发生器能够以较小的阻力代价得到较好的换热效果,表现出较好的综合流动换热性能。比较Case F和Case D的JF因子,Case F的综合换热性能更优,这是因为与Case D形式相比,Case F形式是由Case D与椭圆支柱共同组成的,虽然额外的椭圆支柱造成水流湍流度的增加,使流动阻力增大,但是Case D与椭圆支柱形成的类似喷嘴状流道促进水流加速运动,使对流换热性能得到更大的增强。从上述分析可知,Case F可提供更好的综合流动换热性能,是一种理想的强化换热方式。

|
Download:
|
| 图 11 各矩形通道JF因子比较 Fig. 11 JF factor comparisons among channels | |
本文对布置不同形式纵向涡发生器矩形通道的流动换热性能进行比较,主要结论如下:
1) 计算结果表明CFU式纵向涡发生器能够比CFD式纵向涡发生器提供更好的换热性能;矩形翼纵向涡发生器的换热性能强于对应的三角形翼纵向涡发生器,这表明矩形翼对流体的扰动能力更强,相应的阻力损失也较大。
2) 根据计算结果可知,相同Re下全场体积平均协同角较小的矩形通道对应的对流换热系数较大,这与场协同理论是完全一致的。
3) 综合流动换热性能比较结果表明,Case F的综合流动换热性能最好,能以较小的阻力代价得到较大的换热效果,是一种理想的强化换热方式。
| [1] |
Torri K, Kwak K M, Nishino K. Heat transfer enhancement accompanying pressure-loss reduction with winglet-type vortex generators for fin-tube heat exchangers[J]. International Journal of Heat and Mass Transfer, 2002, 45(18):3795–3801.
DOI:10.1016/S0017-9310(02)00080-7 |
| [2] |
王令, 陈秋炀, 曾敏, 等. 矩形窄通道内带纵向涡发生器的传热强化[J]. 化工学报, 2006, 57(11):2549–2553.
DOI:10.3321/j.issn:0438-1157.2006.11.005 |
| [3] |
Wang Q W, Chen Q Y, Wang L. Experimental study of heat transfer enhancement in narrow rectangular channel with longitudinal vortex generators[J]. Nuclear Engineering and Design, 2007, 237(7):686–693.
DOI:10.1016/j.nucengdes.2006.09.003 |
| [4] |
Chen C, Teng J T, Cheng C H, et al. A study on fluid flow and heat transfer in rectangular microchannels with various longitudinal vortex generators[J]. International Journal of Heat and Mass Transfer, 2014, 69:203–214.
DOI:10.1016/j.ijheatmasstransfer.2013.10.018 |
| [5] |
Ebrahimi A, Roohi E, Kheradmand S. Numerical study of liquid flow and heat transfer in rectangular microchannel with longitudinal vortex generators[J]. Applied Thermal Engineering, 2015, 78:576–583.
DOI:10.1016/j.applthermaleng.2014.12.006 |
| [6] |
何雅玲, 楚攀, 谢涛. 纵向涡发生器在管翅式换热器中的应用及优化[J]. 化工学报, 2012, 63(3):746–760.
|
| [7] |
Wu J M, Zhang H, Yan CH, et al. Experimental study on the performance of a novel fin-tube air heat exchanger with punched longitudinal vortex generator[J]. Energy Conversion and Management, 2012, 57(1):42–48.
|
| [8] |
张强, 王良璧. 通道内矩形涡对涡发生器强化换热的数值研究[J]. 兰州交通大学学报, 2014, 33(6):110–114.
|
| [9] |
Tang L H, Tan S C, Gao P Z, et al. Parameters optimization of fin-and-tube heat exchanger with a novel vortex generator fin by Taguchi method[J]. Heat Transfer Engineering, 2016, 37(3/4):369–381.
|
| [10] |
Tian L T, He Y L, Lei Y G, et al. Numerical study of fluid flow and heat transfer in a flat-plate channel with longitudinal vortex generators by applying field synergy principle analysis[J]. International Communications in Heat and Mass Transfer, 2009, 36:111–120.
DOI:10.1016/j.icheatmasstransfer.2008.10.018 |
| [11] |
唐凌虹, 谭思超, 高璞珍. 纵向涡发生器作用下矩形通道内流动换热性能研究[J]. 原子能科学技术, 2014, 48(5):812–817.
DOI:10.7538/yzk.2014.48.05.0812 |
| [12] |
黄军. 纵向涡作用下窄间隙矩形通道内单相和沸腾流动换热特性机理研究[D]. 西安: 西安交通大学, 2009.
|
| [13] |
Bejan A.
Convective heat transfer[M]. New York: John Wiley & Son Inc, 1995.
|
| [14] |
Holman J P.
Heat transfer[M]. New York: McGraw-Hill Higher Education, 2010: 258.
|
| [15] |
Guo Z Y, Li D Y, Wang B X. A novel concept for convective heat transfer enhancement[J]. International Journal of Heat and Mass Transfer, 1998, 41(14):2221–2225.
DOI:10.1016/S0017-9310(97)00272-X |
| [16] |
Wu J M, Tao W Q. Numerical study on laminar convection heat transfer in a rectangular channel with longitudinal vortex generator. PART A:Verification of field synergy principle[J]. International Journal of Heat and Mass Transfer, 2008, 51(5/6):1179–1191.
|
| [17] |
Yun J Y, Lee K S. Influence of design parameters on the heat transfer and flow friction characteristics of the heat transfer with slit fins[J]. International Journal of Heat and Mass Transfer, 2000, 43(14):2529–2539.
DOI:10.1016/S0017-9310(99)00342-7 |
 2018, Vol. 35
2018, Vol. 35