2. 北京临近空间飞行器系统工程研究所空间物理重点实验室, 北京 100076
2. Science and Technology on Space Physics Laboratory, Beijing Institute of Nearspace Vehicle's Systems Engineering, Beijing 100076, China
添加增韧纤维和遮光剂的SiO2气凝胶复合材料是一种典型的纳米复合隔热材料,由于其具备密度和导热系数低[1-2]、对高温红外辐射有较好的抑制作用[3-4]等优点,近年来在高速飞行器[5]、高温能量存储[6-7]、太阳能高温利用[8]等领域有着广泛应用。
由于纳米复合隔热材料较强的红外辐射衰减特征,其内部红外辐射传输可由Rosseland扩散近似表征[9],因此考虑导热和辐射两种传热方式贡献的等效导热系数为纳米复合隔热材料相关结构热设计、热分析的基础物性参数。在高温实际应用中,材料使用温度高、内部温差大,准确获取不同温度下的等效导热系数显得尤为重要。
基于简化的细观结构、材料组分、孔隙率、块材的物性等参数的理论预测方法是获取纳米复合隔热材料等效导热系数的手段之一,近年来已得到广泛发展[10-13]。理论预测方法对纳米复合隔热材料不同的成分、份额、孔隙率具备较好的适用性。但由于理论预测方法需要对材料的微观结构作一定程度的简化,且纳米复合隔热材料等效导热系数的预测结果基于其各成分的导热系数、光学性质等参数;因而,等效导热系数预测结果的可靠性严重依赖于微观结构的简化程度和材料各成分块材的导热系数和光学常数等参数。而高温下各成分块材的光学性质较为缺乏,通常在计算中采用常温下的数据替代。实验测量的方法可规避理论预测方法存在的上述问题,目前针对纳米复合隔热材料等效导热系数测量的主要实验手段包括热带法(THS)[13]、保护热平板法[14]、平面热源法(hot disk)[15]等。保护热平板法测量获取平板型样品在热、冷两端温度范围内的平均导热系数,不能准确反映材料导热系数随温度的变化。热带法和平面热源法需将样品加热到不同的特定温度,进行多次测量以获取不同温度下的导热系数;实验一般在800 K以下开展。另外,高温测量中样品不同位置温度均匀性难以保证,影响测量精度。
本文发展一种基于瞬态实验测量数据、辐射-导热耦合传热以及遗传算法的随温度变化等效导热系数的智能优化辨识方法。基于待反演参数的灵敏度分析,理论上指导不同参数可能的预测精度;以“数值实验”获取并人工添加不同大小、服从正态分布测量误差的瞬态温度数据作为等效导热系数辨识求解的“实验数据”输入,辨识“数值实验”过程中的等效导热系数,验证了该辨识方法的可靠性;基于真实实验测量获取的高温瞬态温度特性数据,辨识获取纳米复合隔热材料在290~1 090 K范围内的等效导热系数。
1 实验样品和测量装置实验试件的基本成分为SiO2气凝胶,添加SiO2纤维作为增韧剂、SiC颗粒作为遮光剂,孔隙率约为85%,SiO2纤维和SiC颗粒的体积份额分别约为0.5%和4%。试件的长、宽均为300 mm,厚度为L=30 mm。
图 1为实验装置示意图,样品置于两块均热板之间,两均热板分别作为热、冷两端的固体边界。待测样品周围为高温隔热材料以减少边缘的热损失,尽量保证测试过程样品中心区域内传热为一维。样品热端温度TH、中心位置处温度TC采用K型热电偶(omega)进行测量,热电偶测量精度为±2.2 ℃或±0.75%(取较大值);样品冷端温度TL用T型热电偶进行测量,测量精度为±1 ℃或±0.75%(取较大值)。忽略热电偶节点位置的局域非平衡效应以及热电偶与试件之间的接触热阻造成的测量误差,则实验过程中温度测量的最大不确定度估计为6 ℃,瞬态温度实验测量结果见图 2。

|
Download:
|
| 图 1 实验装置示意图 Fig. 1 Schematic of the experimental setup | |

|
Download:
|
| 图 2 实验测量瞬态温度结果 Fig. 2 The measured transient temperature profiles | |
纳米复合隔热材料对红外辐射有一定的穿透能力,其内部温度场可通过求解如下能量方程获得
| $ \rho \left( T \right) {c_{\rm{p}}}\left( T \right)\frac{{\partial T}}{{\partial t}} = \nabla \cdot \left( {{k_{\rm{c}}}\left( T \right)\nabla T} \right) - \nabla \cdot {\mathit{\boldsymbol{q}}_{\rm{r}}}, $ | (1) |
式中:ρ(T),cp(T)和kc(T)分别为纳米复合隔热材料的密度、比热和导热系数;辐射热流密度散度qr[9]定义为
| $ \nabla \cdot {\mathit{\boldsymbol{q}}_{\rm{r}}} = \int\limits_0^\infty {\left[ {4{\rm{ \mathit{ π} }}n_\lambda ^2{I_{{\rm{b}},\lambda }}\left( {T\left( {\hat r,t} \right)} \right) - {G_\lambda }\left( {\hat r} \right)} \right]{\rm{d}}\lambda } , $ | (2) |
式中:Ib, λ(T(
| $ {\mathit{\boldsymbol{q}}_{\rm{r}}} = - \nabla \cdot \left( {\frac{{16{n^2}\sigma {T^3}}}{{3{\beta _{\rm{R}}}}}\nabla T} \right) = - \nabla \cdot \left( {{k_{\rm{r}}}\left( T \right)\nabla T} \right), $ | (3) |
式中:σ为Stefan-Boltzmann常数(σ=5.67×10-8 W·m-2·K-4);βR为Rosseland平均衰减系数。故纳米复合隔热材料的等效导热系数可表达为
| $ {k_{{\rm{eff}}}}\left( T \right) = {k_{\rm{c}}}\left( T \right) + {k_{\rm{r}}}\left( T \right). $ | (4) |
对应于图 1所示传热问题的边界、初始条件分别为
| $ T\left( {0,t} \right) = {T_{\rm{H}}}\left( t \right),T\left( {L,t} \right) = {T_{\rm{L}}}\left( t \right),T\left( {x,0} \right) = {T_0}, $ | (5) |
式中:TH(t)和TL(t)分别为高、低温面温度,T0为初始温度,均由实验测量获取。
纳米复合隔热材料的体积比热cv(T)=ρ(T)cp(T)可由材料内各组分的体积比热及其含量计算获取。文献[18-19]对SiO2气凝胶材料及SiC遮光剂在0~1 500 ℃范围内的体积比热进行了报道。忽略纳米复合隔热材料内其他杂质对体积比热的影响,其体积比热由下式计算而得
| $ {c_{\rm{v}}}\left( T \right) = {c_{{\rm{v}},{\rm{ae}}}}\left( T \right){f_{{\rm{v}},{\rm{ae}}}} + {c_{{\rm{v}},{\rm{SiC}}}}\left( T \right){f_{{\rm{v}},{\rm{SiC}}}} + \varphi {c_{{\rm{v}},{\rm{g}}}}\left( T \right), $ | (6) |
式中,cv(T)、cv, ae(T)、cv, SiC(T)、cv, g(T)分别为纳米复合隔热材料、SiO2气凝胶、SiC遮光剂和气体的体积比热,而fv, ae和fv, SiC分别对应于SiO2气凝胶和SiC遮光剂的体积分数,φ为材料的孔隙率。
3 纳米复合隔热材料等效导热系数辨识方法 3.1 辨识求解方法为获取纳米复合隔热材料随温度变化的等效导热系数keff(T),本文假设材料在某较小的温度范围内keff(T)随温度呈线性变化,从而可采用一系列离散温度点处的等效导热系数来表征keff(T)。本文取该较小的温度范围为100 K,考虑到本文考察的温度范围290~1 190 K,采用温度分别对应于290,390,……,和1 190 K的等效导热系数k1,k2,……,k10进行keff(T)的表征,从而,辨识求解过程中待辨识的参数个数为10。
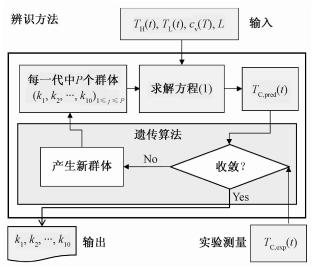
基于群体智能优化的遗传算法是一种自适应、启发式的概率搜索算法,具备较强的鲁棒性和优异的全局搜索能力,适合进行传热问题的多参数辨识求解[20-21]。本文中等效导热系数的辨识求解基于遗传算法,图 3所示为辨识求解流程图。辨识求解中,遗传算法的种群数为P=500,最大进化代数为G=100;依据经验取各待辨识等效导热系数的搜索域为km∈[0.005, 0.05] W/(m·K),其中m=1,2,…,10。首先,遗传算法在等效导热系数的搜索域内随机产生初始群体(k1,k2,…,k10),并结合定解条件、已知参数求解方程(1),获得材料沿厚度方向中心位置的瞬态温度的预测结果TC, pred(t),将预测结果与相应位置的实验测量温度TC, exp(t)进行对比以判定是否满足收敛准则,收敛准则的定义基于如下目标函数的函数值
| $ F = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {1 - {T_{{\rm{C}},{\rm{pred}}}}\left( i \right)/{T_{{\rm{C}},{\rm{exp}}}}\left( i \right)} \right|} , $ | (7) |
|
Download:
|
| 图 3 纳米复合隔热材料等效导热系数辨识过程 Fig. 3 Block diagram of the inverse method for retrieving effective thermal conductivity of nanocomposite thermal insulation | |
式中:TC, exp(i)和TC, pred(i)分别为TC(t)的第i个取样点对应的实验测量和数值预测温度值;N为用于辨识求解的取样点数。本文将F < 1.0×10-3作为辨识过程收敛的准则,辨识过程中若该条件得以满足,则辨识结束并以此时的等效导热系数数据作为辨识结果;若不满足上述收敛条件,遗传算法将对本代群体进行优化并产生新一代群体,进行下一轮方程(1)的求解和收敛条件的判定。若在完成最大遗传代数G=100优化后仍未满足上述收敛条件,则以经100代优化后的参数作为等效导热系数的辨识结果。
3.2 灵敏度分析在辨识求解之前,对待测参数的灵敏度进行分析可有效地指导辨识求解过程。定义待辨识参数的无量纲灵敏度系数为
| $ \chi \left( {{k_m},t} \right) = \frac{{\partial {T_{\rm{C}}}\left( t \right)}}{{\partial {k_m}}}\frac{{{k_m}}}{{{T_{\rm{C}}}\left( t \right)}}. $ | (8) |
由于待测试件等效导热系数未知,而等效导热系数的量级对灵敏度分析的结果可能会有影响,故为保证灵敏度分析的有效性,本文选取文献[22]中添加纤维的SiO2气凝胶材料在不同温度下等效导热系数的理论预测结果(见表 1),结合实验测量获取的边界条件数据(图 2)进行灵敏度分析。
|
|
表 1 文献[22]中纤维增韧SiO2气凝胶等效导热系数 Table 1 Effective thermal conductivities of fiber-reinforced Silica aerogel reported in Ref. [22] |
图 4所示为灵敏度分析结果,其中m=1,2,…,10对应于参数k1,k2,…,k10。由图可知,参数k1~k9具备较高的相对灵敏度,但k10的相对灵敏度较低,因此参数k10可能无法准确辨识获取,即辨识获得的在1 090~1 190 K范围内等效导热系数可能不可靠。另外,多数参数在104 s以内均有较高的灵敏度,因此在后续的辨识过程中,取102~104 s范围内的瞬态温度数据用于辨识求解,其中第一个取样点对应的时刻为t=100 s,之后的取样时间间隔为100 s,对应的取样点数为N=100。

|
Download:
|
| 图 4 等效导热系数灵敏度分析 Fig. 4 Sensitivity of the effective thermal conductivities | |
为验证本文所述辨识方法的可靠性,本研究采用表 1中的等效导热系数数据和实验测量边界温度数据(图 2),数值模拟获取x=L/2位置处的温度数据TC(t),通过人为添加服从正态分布的实验误差作为实验测量值对图 5(a)所示等效导热系数进行重构。此时,测量温度为
| $ {T_{{\rm{mea}}}} = {T_{{\rm{exat}}}} + {\sigma _{\rm{T}}}\xi , $ | (9) |
式中:ξ为服从标准正态分布的随机数,σT为置信度为99%的测量极限误差ΔT的标准差,记为
| $ {\sigma _{\rm{T}}} = \frac{{\Delta T}}{{2.576}}. $ | (10) |
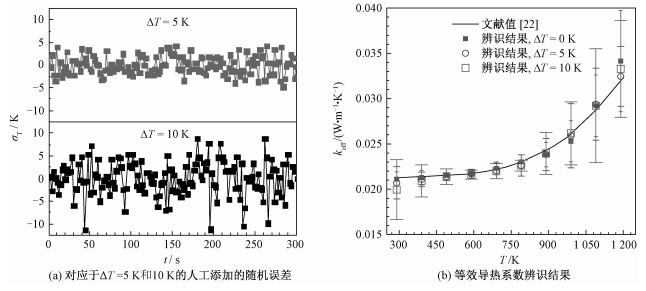
图 5(a)所示为测量极限误差分别为ΔT=5 K和10 K时对应模拟获得的0~300 s内人工添加的实验测量所得温度标准差σT。图 5(b)所示为人为添加极限测量误差分别为ΔT=0,5和10 K时,独立辨识10次所得等效导热系数均值和方差,分别定义为:
| $ {{\bar k}_m} = \frac{1}{{10}}\sum\limits_{i = 1}^{10} {{k_{m,i}}} ,{\sigma _{{k_m}}} = \sqrt {\frac{1}{{10}}\sum\limits_{i = 1}^{10} {{{\left( {{k_{m,i}} - {k_m}} \right)}^2}} } , $ | (11) |
|
Download:
|
| 图 5 基于数值实验温度数据辨识所得等效导热系数 Fig. 5 Effective thermal conductivities retrieved based on numerically generated temperature data | |
式中,km, i为第m个参数的第i次辨识结果。
由图 5(b)可知,在不同的人为添加测量误差条件下,辨识结果方差总体上随添加误差的增大而增大,但本文所述方法均能在上述测量误差条件下给出较为准确的等效导热系数辨识结果,验证了本文所述反演辨识方法的可靠性。另外,温度为1 190 K时的辨识结果和真实结果偏差相对较大,这与灵敏度分析过程中给出的结论一致。
4.2 纳米复合隔热材料等效导热系数辨识结果基于实验测量瞬态温度数据(图 2),对纳米复合隔热材料在氮气气氛、常压、常温到1 090 K范围内等效导热系数独立进行10次辨识并取均值,所得结果见图 6(a),其中的误差限体现10次独立辨识所得结果的方差水平。可见等效导热系数随温度升高呈非线性上升趋势,介于0.027~0.043 W/(m·K)。文献[12]报道与本文成分、各成分的份额、材料的孔隙率等参数均相近的纳米复合隔热材料在常压、300~1 000 K范围内的等效导热系数理论预测结果,其中预测过程中材料的微观结构基于DLCA (diffusion-limited cluster-cluster aggregation)方法建立,材料的辐射特性基于常温下其成分的光学性质和Lorenz-Mie散射理论计算而得。本文的辨识结果比文献[12]中报道的理论预测结果普遍低20%~35%,造成该现象的原因可能包括:1)本文用于实验测量的纳米复合隔热材料内可能存在未知热性质的杂质;2)文献[12]中基于DLCA方法生成的纳米复合隔热材料微观结构与本文测试样件的真实结构之间存在差异;3)由于高温光学性质缺乏,且不同文献报道的SiC材料在常温下的光学性质差异极大[23-24],因而,基于SiC块材在常温下的光学性质和Lorenz-Mie散射理论可能无法准确预测获取纳米复合隔热材料中SiC遮光剂在不同温度下的辐射特性,从而影响等效导热系数的预测结果。

|
Download:
|
| 图 6 纳米复合隔热材料等效导热系数辨识结果 Fig. 6 The retrieved effective thermal conductivities of nanocomposite thermal insulation | |
图 6(b)所示为基于辨识获得的等效导热系数求解方程(1)所得材料在x=L/2位置处的瞬态温度与相应的实验测量瞬态温度的对比情况。可见,二者吻合良好,在不同时刻下的最大偏差不超过1.0%,说明辨识获取的等效导热系数参数可用于纳米复合隔热材料瞬态热特性的准确预测。
5 结论本文以瞬态实验测量数据为基础,结合基于Rosseland扩散近似的辐射-导热耦合传热模型以及遗传算法,建立随温度变化的等效导热系数辨识模型。在以数值实验为基础,验证反演辨识模型可靠性的基础上,基于高温瞬态实验测量数据,辨识获取纳米复合隔热材料在常压氮气气氛中,温度为290~1 090 K范围内纳米隔热材料的等效导热系数,辨识结果介于0.027~0.043 W/(m·K),随温度升高呈现出非线性上升趋势。本研究所述辨识方法还可为其他隔热材料在不同温度下的等效导热系数辨识提供一种可靠的途径。
| [1] |
He Y L, Xie T. Advances of thermal conductivity models of nanoscale silica aerogel insulation material[J]. Applied Thermal Engineering, 2015, 81:28–50.
DOI:10.1016/j.applthermaleng.2015.02.013 |
| [2] |
Lu G, Wang X D, Duan Y Y, et al. Effects of non-ideal structures and high temperatures on the insulation properties of aerogel-based composite materials[J]. Journal of Non-Crystalline Solids, 2011, 357(22/23):3822–3829.
|
| [3] |
赵俊杰, 段远源, 王晓东, 等. 纳米复合隔热材料辐射与导热耦合传热[J]. 工程热物理学报, 2012, 33(12):2185–2189.
|
| [4] |
Zhao J J, Duan Y Y, Wang X D, et al. Optical and radiative properties of infrared opacifier particles loaded in silica aerogels for high temperature thermal insulation[J]. International Journal of Thermal Sciences, 2013, 70(8):54–64.
|
| [5] |
Fesmire J E. Aerogel insulation systems for space launch applications[J]. Cryogenics, 2006, 46(2/3):111–117.
|
| [6] |
Maloney R P. High surface area aerogels for energy storage and efficiency[D]. East Lansing: Michigan State University, 2012.
|
| [7] |
Carrington K R. Fabrication and optimization of nano-structured composites for energy storage[D]. Berkeley: University of California, Berkeley, 2009.
|
| [8] |
Reim M, Beck A, Korner W, et al. Highly insulating aerogel glazing for solar energy usage[J]. Solar Energy, 2002, 72(1):21–29.
DOI:10.1016/S0038-092X(01)00086-X |
| [9] |
Modest M F.
Radiative Heat Transfer[M].2nd ed. San Diego, CA: Academic Press, 2003.
|
| [10] |
Zeng S Q, Hunt A, Greif R. Geometric structure and thermal conductivity of porous medium silica aerogel[J]. ASME Journal of Heat Transfer, 1995, 117(4):1055–1058.
DOI:10.1115/1.2836281 |
| [11] |
Xie T, He Y L, Hu Z J. Theoretical study on thermal conductivities of silica aerogel composite insulating material[J]. International Journal of Heat and Mass Transfer, 2013, 58(1/2):540–552.
|
| [12] |
Fang W Z, Zhang H, Tao W Q. Numerical predictions of thermal conductivities for the silica aerogel and its composites[J]. Applied Thermal Engineering, 2017, 115:1277–1286.
DOI:10.1016/j.applthermaleng.2016.10.184 |
| [13] |
Wei G S, Liu Y S, Zhang X X, et al. Thermal conductivities study on silica aerogel and its composite insulation materials[J]. International Journal of Heat and Mass Transfer, 2011, 54(11/12):2355–2366.
|
| [14] |
Lee D, Stevens P C, Zeng S Q, et al. Thermal characterization of carbon-opacified silica aerogels[J]. Journal of Non-Crystalline Solids, 1995, 186(2):285–290.
|
| [15] |
Zhang H, Jin Y, Wei G, et al. A numerical study on the influence of insulating layer of the hot disk sensor on the thermal conductivity measuring accuracy[J]. Progress in Computational Fluid Dynamics, 2013, 13(3/4):191–201.
DOI:10.1504/PCFD.2013.053660 |
| [16] |
Zeng J S Q, Greif R. Effective optical constants n and k and extinction coefficient of silica aerogel[J]. Journal of Materials Research, 1996, 11(3):687–693.
DOI:10.1557/JMR.1996.0083 |
| [17] |
Bellunato T, Calvi M, Matteuzzi C, et al. Refractive index of silica aerogel:uniformity and dispersion law[J]. Nuclear Instruments and Methods in Physics Research A, 2008, 595(1):183–186.
DOI:10.1016/j.nima.2008.07.072 |
| [18] |
杨景兴, 何凤梅, 于帆, 等. SiO2气凝胶热参数测试及评价[J]. 宇航材料工艺, 2013, 43(2):92–94.
|
| [19] |
Munro R G. Material properties of a sintered a-SiC[J]. Journal of Physical and Chemical Reference Data, 1997, 26(5):1195–1203.
DOI:10.1063/1.556000 |
| [20] |
Czél B, Gróf G. Inverse identification of temperature-dependent thermal conductivity via genetic algorithm with cost function-based rearrangement of genes[J]. International Journal of Heat and Mass Transfer, 2012, 55(15/16):4254–4263.
|
| [21] |
Gosselin L, Tye-Gingras M, Mathieu-Potvin F. Review of utilization of genetic algorithms in heat transfer problems[J]. International Journal of Heat and Mass Transfer, 2009, 52(9/10):2169–2188.
|
| [22] |
Zhao J J, Duan Y Y, Wang X D, et al. An analytical model for combined radiative and conductive heat transfer in fiber-loaded silica aerogels[J]. Journal of Non-Crystalline Solids, 2012, 358(10):1303–1312.
DOI:10.1016/j.jnoncrysol.2012.02.037 |
| [23] |
Palik E D.
Hand book of optical constants of solids[M]. San Diego, CA: Academic Press, 1985.
|
| [24] |
Pégourié B. Optical properties of a silicon carbide[J]. Astronomy and Astrophysics, 1988, 194:335–339.
|
 2018, Vol. 35
2018, Vol. 35 


