2. 中国核动力研究设计院, 成都 610213;
3. 哈尔滨电气股份有限公司, 哈尔滨 150028
2. Nuclear Power Institute of China, Chengdu 610213, China;
3. Harbin Electric Company Limited, Harbin 150028, China
变换光学作为一种设计方式,可以使电磁波、流体波、物质波等在空间内产生弯曲。而若要实现这种弯曲,则必须要满足相关的控制方程在经历空间变换之后能够具有形式不变性。Pendry等[1]考虑Maxwell方程不变性,将电磁传输与坐标变换相关联,从而将材料的导电特性等特征参数与空间坐标形成映射关系,设计出能够使电磁波弯曲的电磁斗篷;Fan等[2]通过研究发现,在一定的条件下热扩散方程具有形式不变性,并设计球形和椭球形的热斗篷。而这也为热斗篷的设计提供了理论上的依据;Guenneau和Amra[3]引入雅可比矩阵对热传导方程进行坐标变换与推导,将变换光学的理论拓展到变换热力学领域,并通过求解非稳态导热微分方程设计二维圆形热斗篷与热集中器;Schittny等[4]通过将铜和聚二甲硅氧烷(PDMS)交替填充设计二维圆形热斗篷,并首次通过实验观测到瞬态传热的温度梯度分布;Narayana等[5]基于超材料设计不同厚度防护层的二维圆形热斗篷,并通过实验验证其防护特性;Han等[6]通过对普通材料进行周期性的排列,设计二维圆形热斗篷以及三维球形热斗篷,并通过实验对结果的可靠性进行验证;Wu[7]利用汉密尔顿运动方程对热流路径进行了设计,为圆柱形热斗篷的设计提供了依据。Xu等[8]设计一种超薄的三维热斗篷,并通过实验成功地对防护区域内的空气泡实现热力学隐身;毛福春等[9]通过变换热力学的理论,推导并验证二维任意截面非共形热斗篷的导热系数表达式;Vemuri和Bandaru[10]通过对复合结构的研究发现控制热流偏转基本原理,并提出热流偏角的概念。Yang等[11]在他们的研究结果的基础上,发现各向同性的材料经过复合之后其导热系数会表现出各向异性的特征,并通过实验观测到材料层本构参数的改变对热流偏角的影响;Canbazoglu等[12]通过实验研究二维热流偏角与导热系数和防护材料层厚度的关系,结果表明:导热系数与材料层厚度越大,热流偏角越大,但是导热系数对热流偏角的影响较大。
由于热流绕过热斗篷区域可以使被保护物体保持较低的温度,但热斗篷结构对外界环境的热流分布会产生一定影响。因此为设计高效且对外界环境影响较小的热斗篷,对由于热流绕流产生的热流偏角的控制十分重要。目前,学者们的研究基本是考虑二维条状交替分布的材料引起的热流偏角,而对于圆形热斗篷的热流偏角的研究却鲜有报道。因此本文将以铜和PDMS材料交替复合的热斗篷结构为基础,应用变换光学的理论推导出空间内任意位置热流偏角的表达式。并通过Fluent 14.0对二维结构热斗篷的热流偏角进行计算,验证该表达式的正确性并总结影响圆形产生的热流偏角大小的因素。
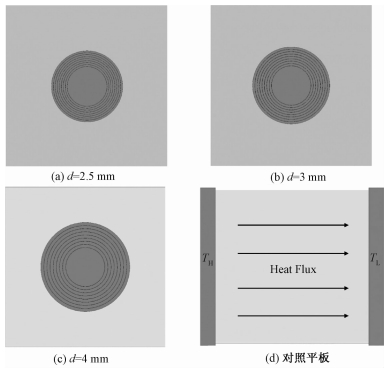
1 物理模型与理论方法 1.1 物理模型本文为探究热流偏角的影响因素,分别建立了不同厚度的8层二维圆形热斗篷结构模型。热斗篷模型包含3部分:背景平板,热斗篷区域,保护区域。在本文中,保护区域内放置一个半径为r0=25 mm的铜圆板作为被保护体。根据Schittny等[4]的实验,本文设计了材料层厚度分别为d1=2.5 mm,d2=3 mm,d3=4 mm的圆形热斗,且热斗篷区域也采用铜和PDMS交替的复合结构来满足所需要的导热系数,其中铜的导热系数为kCu=398 W/(m·K),PDMS的导热系数为kPDMS=0.15 W/(m·K)。根据文献[3]中的公式(24)对每层内的导热系数进行计算,各层的导热系数(单位为W/(m·K))分别为k1=0.15,k2=397.25,k3=2.83,k4=394.07,k5=11.32,k6=384.91,k7=18.36,k8=377.52。考虑到实际加工工艺的复杂性,背景平板材料选取铝合金(92Al-8Mn),其导热系数为kb=107 W/(m·K)。其中,二维背景平板为204 mm×204 mm正方形计算域。计算模型如图 1所示。
|
Download:
|
| 图 1 计算模型 Fig. 1 Computation models | |
导热微分方程是用来描述热量从高温区域流向低温区域的过程,传热过程中的热量与物质的密度、比热容、导热系数、温度梯度和热源等有关。在笛卡尔坐标系下,其可以表述为
| $ \rho c\frac{{\partial T}}{{\partial t}} = \nabla \cdot \left( {{k_x}\nabla T} \right) + \nabla \cdot \left( {{k_y}\nabla T} \right) + Q. $ | (1) |
式中:ρ表示物质的密度;c表示物质的比热容;kx,ky分别为物质的导热系数在笛卡尔坐标系中x,y方向的分量;T为物质的温度;∇表示梯度场。考虑到所研究热斗篷结构的传热为无内热源传热过程,则Q=0,由于该传热过程为稳态过程,因此∇·(k∇T)=0。因此,该过程的传热微分方程具有形式不变性,综合变换光学的理论,其可以表述为
| $ \nabla ' \cdot \left( {k'\nabla 'T'} \right) = 0. $ | (2) |
式中:k′,T′分别表示变换坐标之后的物质的导热系数与温度;∇′为变换坐标之后的梯度。
考虑到所研究热斗篷结构为多层复合材料热斗篷,因此,将其变换到极坐标系进行研究;同时为实现热隐身,考虑到不同层内各向异性的导热特性,需将所求得极坐标系沿径向作如下变换[3]:
| $ \left\{ \begin{array}{l} r' = {R_{i + 1}} + \frac{{\left( {{R_{i + 1}} - {R_i}} \right)}}{{{R_{i + 1}}}}r\\ \theta ' = \theta , \end{array} \right.,\left( {i \ge 1} \right). $ | (3) |
综合两次坐标变换x(x, y)→r(r, θ) →r′(r′, θ′),引入雅可比矩阵,不同坐标系下的导热系数关系为
| $ {{k'}_{ij}} = \frac{{\mathit{\boldsymbol{J}}{k_{ij}}\mathit{\boldsymbol{J'}}}}{{\det \left( \mathit{\boldsymbol{J}} \right)}}. $ | (4) |
式中:J为雅可比矩阵,det(J)为雅可比矩阵行列式,i为热斗篷的层数。文献[10]的公式(3)给出笛卡尔坐标系下不同方向上导热系数的分量[10],考虑到不同层内导热系数与防护层厚度的不同,笛卡尔坐标系下任意点的导热系数可以表示为
| $ {k_{ij}} = \left( {\begin{array}{*{20}{c}} {\frac{{\left( {{l_{i + 1}} + {l_i}} \right){k_{i + 1}}{k_i}}}{{{l_{i + 1}}{k_i} + {l_i}{k_{i + 1}}}}}&0\\ 0&{\frac{{{k_{i + 1}}{l_{i + 1}} + {k_i}{l_i}}}{{{l_{i + 1}} + {l_i}}}} \end{array}} \right). $ | (5) |
将式(5),式(6)代入到式(4)中,经过矩阵运算可得
| $ {{k'}_{ij}} = \left[ {\begin{array}{*{20}{c}} {{{k'}_{11}}}&{{{k'}_{12}}}\\ {{{k'}_{21}}}&{{{k'}_{22}}} \end{array}} \right]. $ | (6) |
式中:
| $ \begin{array}{l} {{k'}_{11}} = {\left( {r' - {R_i}} \right)^2}\left( {{k_x}{{\cos }^2}\theta ' + {k_y}{{\sin }^2}\theta '} \right),\\ {{k'}_{21}} = r'\left( {r' - {R_i}} \right)\sin \theta '\cos \theta '\left( { - {k_x} + {k_y}} \right). \end{array} $ | (7) |
根据傅里叶定律可知
| $ \left( {\begin{array}{*{20}{c}} {{{q'}_r}}\\ {{{q'}_\theta }} \end{array}} \right) = - \left[ {\begin{array}{*{20}{c}} {{{k'}_{11}}}&{{{k'}_{12}}}\\ {{{k'}_{21}}}&{{{k'}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\partial T/\partial r'}\\ {\partial T/\partial \theta '} \end{array}} \right]. $ | (8) |
由于笛卡尔坐标系中沿x方向上的温度梯度为给定常数,因此,沿r′方向热流密度分布可以表示为
| $ \begin{array}{l} {{q'}_r} = - {{k'}_{11}}\nabla {T_{r'}},\\ {{q'}_\theta } = - {{k'}_{21}}\nabla {T_{r'}}. \end{array} $ | (9) |
通过以上推导,可以得出空间内沿径向任意点的热流偏角
| $ \begin{array}{l} {\phi _1} = {\tan ^{ - 1}}\left( {\frac{{{{q'}_\theta }}}{{{{q'}_r}}}} \right)\\ \;\;\;\; = {\tan ^{ - 1}}\left[ {\frac{{a\sin \theta '\cos \theta '\left( {{k_y} - {k_x}} \right)}}{{\left( {{k_x}{{\cos }^2}\theta ' + {k_y}{{\sin }^2}\theta '} \right)}}} \right]. \end{array} $ | (10) |
方程(10)给出极坐标系空间内任一点处的热流偏角的计算方法,其中a=r′/(r′-Ri)为坐标点沿径向位置分布的影响系数。当材料层仅绕z轴转动,即r=r′时,方程(10)可以简化为文献[10]中的公式(9)的形式。文献[10]考虑了空间旋转(θ)对于热流偏角的影响,此时r=r′且Ri=Ri+1=0;本文在此基础之上,考虑坐标变换径向距离改变对于热斗篷材料层内热流偏角的影响,并提出公式(10)。本文利用FLUENT对不同热斗篷结构的热传导过程进行数值模拟,基于数值模拟结果获得不同材料层内的热流偏角,并且将其与公式(10)的直接计算结果相对比,二者的结果相近,因此,可以看作是利用FLUENT的模拟结果对所推导的公式(10)进行了验证。因此,该推导结果可以描述任意形状的热斗篷的热流偏角,并作为对Vemuri等[10]的工作的补充与扩展。
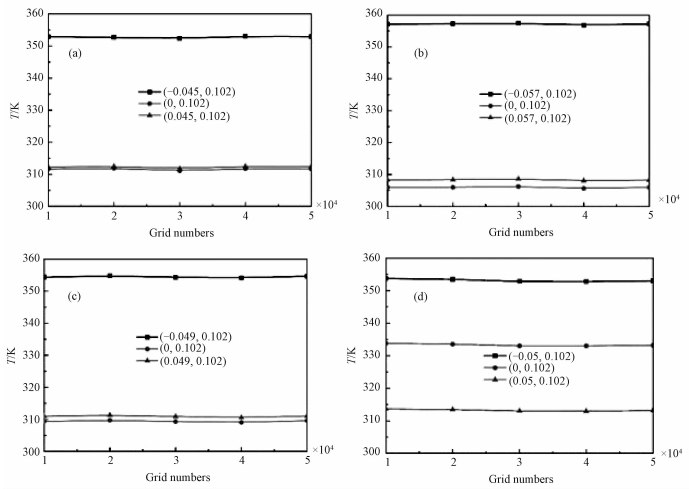
2 结果与讨论为比较不同材料层厚度对热流偏角变化的影响,本文采用FLUENT分别对材料层厚度为2.5、3和4 mm的圆形热斗篷结构的传热过程进行数值模拟。本文选取定壁温边界条件[2-12](第一类边界条件),即左壁面温度恒定为373 K,右壁面温度恒定为293 K,环境温度设置为293 K;并以此为初始条件,在热隐身斗篷模型内对无内热源非稳态导热微分方程进行求解。考虑到传热过程为瞬时变化,开启瞬态求解器。由于复合结构导热系数的变化为非线性变化,为观测到明显的“热隐身”效果,该结构的计算时间为600 s。网格划分时,对每种模型绘制网格数分别为1×104,2×104,3×104,4×104,5×104的结构化网格,每种网格经计算600 s后,利用3个测点温度分布进行网格无关性验证,各种结构在不同网格数的温度值如图 2所示,模拟温度场分布如图 3所示。
|
Download:
|
| 图 2 各种结构不同网格数的测点温度 Fig. 2 Temperatures at the measuring points in different models with various grids | |
|
Download:
|
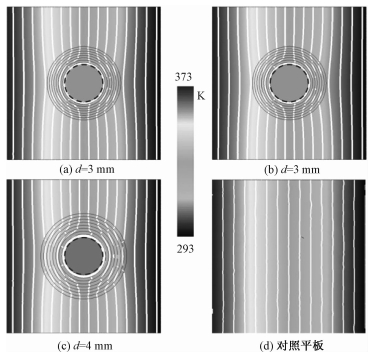
| 图 3 600 s时不同材料层厚度的热斗篷的温度分布 Fig. 3 Temperature distributions for different models at 600 s | |
选取中心点,以及背景材料与隐身区域交点为测点,对比各种结构在不同网格数的温度值。从图 2可以看出,所选取测点温度在不同网格数时,波动范围极小;因此可以认为该结构的传热过程与网格密度无关。
从图 3可以看出,相对于对照平板,当热流经过热斗篷区域时,热流会发生不同程度的偏转,从而使不同材料层厚度的热斗篷起到“热隐身”作用;且在3组不同结构中,当材料层厚度为4 mm时热斗篷的隐身效果最为明显。这说明,热斗篷复合材料层的厚度对于“热隐身”的效果具有一定的影响。随着材料层厚度的增加,保护区域的中心温度也相应地降低,温度梯度的变化相对较慢,从而使得具有较厚材料层的“隐身”效果较为明显。而造成这种现象的原因,可以从热流偏角的角度进行诠释。
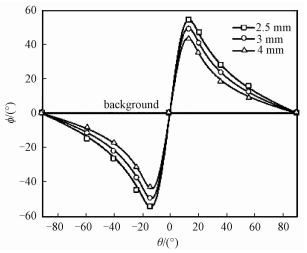
图 4给出前文所述的3种不同结构热斗篷的第1层和第2层材料层的交界处(图 3中红色曲线标记处)的热流偏角的变化情况。由图 4可以看出,各个结构的热流偏角变化规律均相同,根据式(10)可知,在各个方向导热系数一定的条件下,热流偏角的大小主要取决于轴向的偏转角(θ)以及径向的位置。因此,对于热流偏角的极值(峰值)位置的求解,可以通过对式(10)求导来完成,当式(10)的导数为0时,即
|
Download:
|
| 图 4 第一和第二材料层交界处的热流偏角 Fig. 4 Heat flux bending in the interfaces between the first and second material layers | |
这说明,当θ一定时,材料层厚度较小的热斗篷所引起的热流偏转程度较大,可以使热通量沿着径向方向传播的分量较大,使得沿轴向的热通量较小,因此对于热流的传播作用阻碍较小,热量可以相对较快地沿径向方向传播。当增大材料层厚度时,热流偏转程度较小,造成热通量的径向分量减小,轴向分量增大;使热流能够更为贴紧交界面进行传递,从而令热量在材料层中集聚较多,又因为材料层的导热系数为交替变化,因此对于热流的传递能够起到延缓作用。
综合来看,当材料层厚度较大时,可以使热流偏转程度降低,较多的热量耗散发生在材料层内。使得进入保护区域的热通量较小,从而造成温度的涨落较小,热斗篷起到较好的“热隐身”作用。
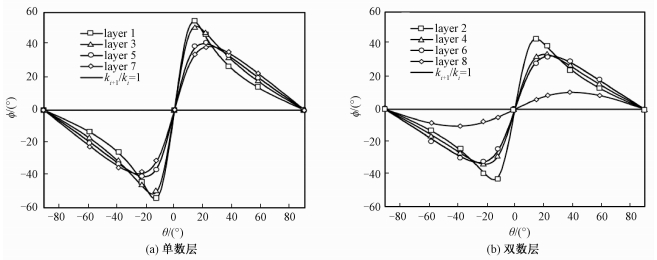
经过前述推导可知热流偏角可以通过改变材料的导热系数、材料层的厚度,以及空间点的分布来控制热流偏角的大小。为探究所设计结构各边界层热流偏角的变化,选取材料层厚度为2.5 mm的热斗篷为研究对象,各边界层处导热系数的比值(b=ki+1/ki)分别为:b1=2 648.33,b2=0.007 124,b3=139.247 3,b4=0.028 726,b5=34.002 6,b6= 0.047 699,b7=20.562 09,b8=0.283 43。其各边界层的热流偏角如图 5所示。
|
Download:
|
| 图 5 d1=2.5 mm的热斗篷各边界层处热流偏角 Fig. 5 Heat flux bending in each interface in the cloaking scheme with d1=2.5 mm | |
为方便分析,图 5(a)表示的是第1、3、5、7边界层处的热流偏角,即b > 1。图 5(b)表示的是第2、4、6、8边界层处的热流偏角,即b < 1。从图 5可以看出,各层内的热流偏角变化规律均相同。当-90° < θ < 0°时,热流偏角均随着θ的增大而先增大,当θ达到一定值时,热流偏角开始迅速减小直到θ为0°时,热流偏角为0°,即热流不发生偏转;热流偏角的最大值在第1层内为最大,第7层内为最小,且其值由内层至外层逐层减小;各层内热流偏角在达到最大之前,其变化率由内层至外层逐层增大;当θ达到一定值后逐渐减小到0°时,其变化率由内层至外层逐层减小。当0° < θ < 90°时,热流偏角均随着θ的增大而先迅速增大,当θ达到一定值时,热流偏角开始缓慢减小直到θ为90°时,热流偏角为0°,即热流不发生偏转;热流偏角的最大值在第1层内为最大,第7层内为最小,且其值由内层至外层逐层减小;各层内热流偏角在达到最大之前,其变化率由内层至外层逐层减小;当θ达到一定值后逐渐增大到90°时,其变化率由内层至外层逐层增大。热流偏角相对径向呈对称。这表明,当θ一定且b > 1时,随着b的减小,热流偏转的角度随之减小;当θ一定且b < 1时,随着b的增大,热流偏转的角度随之减小;当b=1时,热流不发生偏转。
综合图 5(a)和5(b)可知,奇数层(b > 1)和偶数层(b < 1)内热流偏角变化趋势相同,但双数层的热流偏角明显小于与之相邻的单数层的热流偏角。这是由于相邻层之间的导热系数相差较大,导致热量在导热系数较小的层内大量耗散,使得热流在导热系数较小的层内传递较慢,使得热流偏转程度降低;而在导热系数较大的层内热流快速传递,使得热流偏转程度增大。因此,造成不同材料层内热流偏角存在差异,即导热系数比值不相同,热流偏角的位置会不相同。
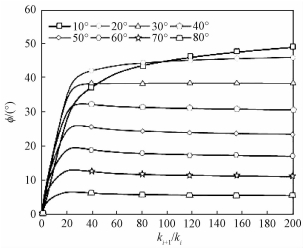
图 6给出当θ一定时,热流偏角随b的变化趋势。从图中可以看出,随着b的增加热流偏角开始快速增大;当b增大到一定时,热流偏角的变化率减小,热流偏角在极小的范围内波动。这说明,随着b的增大,热流偏角不会持续增大,而是在达到一定值时,热流偏转程度达到平衡。当θ不同时,相应的热流偏角也会随之改变。随着θ的增大,热流偏角稳定时的值也会相应地增大。
|
Download:
|
| 图 6 θ一定时的热流偏转角 Fig. 6 Values of the heat flux bending when θ is constant | |
本文利用变换光学的方法,推导出二维空间内任意位置点的热流偏角表达式,当a=1(即r取单位长度)时,所得结果与文献[10]中的公式(9)一致。并通过FLUENT对二维圆形热斗篷模拟进行验证。分析二维圆形热斗篷个材料层边界处的热流偏转角变化情况,结果表明:随着材料层厚度的增加,热流偏转角变化率减小,热流传递较为平稳,进入保护区域的热通量较小。热流在各材料层间进行传递时,其偏转程度与相邻两层的导热系数比值b相关;当b > 1时,热流偏转的程度随着b的增大而增大;当b < 1时,热流偏转的程度随着b的增大而减小;当θ一定时,热流偏转角随着b的增大而先增大后趋于稳定。本文考虑二维多层结构圆形热斗篷的热流偏角变化,并提出空间内任意位置的热流偏角表达式,可为以后在三维空间内控制热流的传递路径的研究提供设计依据。
| [1] |
Pendry J B, Schurig D, Smith D R. Controlling electromagnetic fields[J]. Science, 2006, 312(5781):1780–1782.
DOI:10.1126/science.1125907 |
| [2] |
Fan C Z, Gao Y, Huang J P. Shaped graded materials with an apparent negative thermal conductivity[J]. Appl Phys Lett, 2008, 92(25):251907.
DOI:10.1063/1.2951600 |
| [3] |
Guenneau S, Amra C. Anisotropic conductivity rotates heat fluxes in transient regimes[J]. Opt Express, 2013, 21(5):6578–6583.
DOI:10.1364/OE.21.006578 |
| [4] |
Schittny R, Kadic M, Guenneau S, et al. Experiments on transformation thermodynamics:molding the flow of heat[J]. Phys Rev Lett, 2013, 110(19):195901.
DOI:10.1103/PhysRevLett.110.195901 |
| [5] |
Narayana S, Savo S, Sato Y. Transient heat flux shielding using thermal metamaterials[J]. Appl Phys Lett, 2013, 102(20):201904.
DOI:10.1063/1.4807744 |
| [6] |
Han T, Bai X, Gao D, et al. Experimental demonstration of a bilayer thermal cloak[J]. Phys Rev Lett, 2014, 112(5):054302.
DOI:10.1103/PhysRevLett.112.054302 |
| [7] |
Wu L. Cylindrical thermal cloak based on the path design of heat flux[J]. J Heat Trans, 2015, 137(2):021301.
DOI:10.1115/1.4028920 |
| [8] |
Xu H, Shi X, Gao F, et al. Ultrathin three-dimensional thermal cloak[J]. Phys Rev Lett, 2014, 112(5):054301.
DOI:10.1103/PhysRevLett.112.054301 |
| [9] |
毛福春, 李廷华, 黄铭, 等. 任意横截面柱形热斗篷研究与设计[J]. 物理学报, 2014, 63(1):14401.
DOI:10.7498/aps.63.014401 |
| [10] |
Vemuri K P, Bandaru P R. Geometrical considerations in the control and manipulation of conductive heat flux in multilayered thermal metamaterials[J]. Appl Phys Lett, 2013, 103(13):133111.
DOI:10.1063/1.4823455 |
| [11] |
Yang T, Vemuri K P, Bandaru P R. Experimental evidence for the bending of heat flux in a thermal metamaterial[J]. Appl Phys Lett, 2014, 105(8):083908.
DOI:10.1063/1.4894387 |
| [12] |
Canbazoglu F M, Vemuri K P, Bandaru P R. Estimating interfacial thermal conductivity in metamaterials through heat flux mapping[J]. Appl Phys Lett, 2015, 106(14):143904.
DOI:10.1063/1.4917344 |
 2018, Vol. 35
2018, Vol. 35 


