2. 清华大学能源与动力工程系工程热物理研究所, 北京 100081
2. Insitute of Engineering Thermophysics, Department of Energy and Power Engineering, Tsinghua University, Beijing 100081, China
孔隙率和渗透率是多孔介质内传热传质过程中非常重要参数,其研究对岩土工程领域、建筑工程领域、石油开采领域、环境保护领域、化学工程领域等的相关过程有重要的指导意义。通常研究认为,在大于表征元(REV)尺度、假定孔隙均匀分布的情况下,渗透率和孔隙率之间呈现一种确定函数关系,甚至对规则堆积的多孔介质,存在着回归意义上的渗透率公式,最著名的如Ergon公式[1]、Kozeny-Carman公式[2]等,其已经被广泛应用于多孔介质内质传递过程的预估。对于自然界广泛存在的各类真实多孔介质,虽然在工程实践中为方便处理,被认为是存在平均意义上的孔隙率,且孔隙率大小和方向性可以用孔隙率张量描述,但实际上,当多孔介质尺度和孔隙尺度相比不大、小于表征元尺度时,孔隙分布均匀这一假设就不再成立,实际孔隙分布会存在各向不一致、少量优势大孔隙和数目众多的小孔隙、死隙并存的现象,这种孔隙分布的不均匀性会导致传热传质过程中无法统一量化的局部效应变得非常明显。
目前对于实际多孔体渗透特性的研究中,有一种非常流行的手段是采用CT或核磁共振方法对实际多孔体经典样本进行三维扫描断层,之后在计算机里进行三维重构[3-6],并以此数字化样本为基础,对其进行孔隙率、渗透率研究。这种研究方法合理性显而易见,目前采用这种方法进行多孔介质渗透特性研究的文章非常多,涉及前面提及的各个领域,但是这种方法的不足也非常明显:例如得到的孔隙率大小、分布和采取手段的空间分辨率相关,目前报道的分辨率最佳大约在1 μm量级,1 μm量级以下的孔隙无法识别,被认为是骨架一部分,而这些小孔隙数目众多,虽对传热传质的贡献不如优势大孔隙,但对整体渗流的影响不可轻易忽略;其次,这样的小尺度多孔介质,即使宏观上孔隙率大小相等,但是由于微观孔隙大小、方向分布不一致,会对它的渗透特性,乃至对于整个取样主体的多孔介质渗透特性有巨大影响。本文旨在孔隙尺度下,对孔隙率损失和渗透率损失的相关性及其孔隙率大小相同而孔隙分布不同而导致渗透率畸变特性进行研究。
目前从采用多孔介质三维重构并进行渗透特性的研究来看,通常各个二维断面上多孔介质片(或者说是二维多孔体)的渗透率,通常比宏观三维渗流率要大,且各个断面上的二维多孔体片渗透特性从某种意义上决定三维多孔体的渗透特性。因此,本文相关研究从二维尺度展开,对孔隙率损失和渗透率损失的相关性、及其孔隙率大小相等而孔隙分布不均匀的异构二维多孔体渗透特性进行研究。
为便于讨论,本文选择有一定代表性的、且比较规范的小圆(柱)填充的二维多孔体,生成多孔体骨架的小圆用此圆域内坐标整点的全体代表,本文同孔隙率大小、孔隙分布不同的异构多孔体样本的获得,是通过保证同宏观尺寸给定分辨率网格中多孔骨架拥有相同整点个数的方法来实现的,因此是绝对意义上的孔隙率相等。同孔隙率异构的孔隙率样本非常多,为方便起见,本文只是选取其中6个由2个不同直径圆柱组成的同孔隙率异构样本进行相关规律探讨。
当多孔介质孔隙尺度小到一定程度,若以气体为流动工质,气体渗透时会有稀薄滑移效应,也称为克灵伯格滑脱效应。目前气体滑移理论[7]认为:气体在Kn < 0.01,可适用连续流体理论;在0.01≤Kn < 0.1时,可以视为过渡流;在Kn≥0.1时,可以适用分子动力学。本文的孔隙尺度选择范围为Kn < 0.01,不考虑存在滑移情况,对于有滑移情况下,边界处必须考虑滑移效应,将在后续论文中讨论。
1 MRT LBM模型近年来,格子Boltzmann方法作为一种流体力学介观尺度的数值研究方法,凭借其独特的优势,被成功地应用到单相流体、多相流体在多孔介质中的传热传质研究领域。在格子Boltzmann方法中,最为常用的是单松弛时间的BGK模型,但是该模型有2个不足:一是数值稳定性差,二是松弛时间的选择会对流动特性有影响[8-10]。因此若采用单松弛时间模型研究多孔介质渗透率,可能导致得到的渗透率与黏性相关。因此,本文采用被广泛认定为计算得到渗透率和黏性无关的MRT LBM模型进行二维多孔介质渗透率特性的研究。
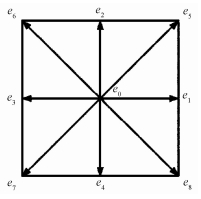
1.1 D2Q9 MRT LBM模型简述文献[7-9]表明,在使用LBM单松弛模型时会导致渗透率计算和采取的计算松弛时间的黏度相关,故本文多松弛时间格子-Boltzmann模型(MRT LBM),并选取二维九速模型(D2Q9)为计算基础,该模型9个方向单位矢量间的关系如图 1。
| $ {e_\alpha } = c\left[ {\begin{array}{*{20}{c}} 0&1&0&{ - 1}&0&1&{ - 1}&{ - 1}&1\\ 0&0&1&0&{ - 1}&1&1&{ - 1}&{ - 1} \end{array}} \right] $ |
|
Download:
|
| 图 1 D2Q9模型 Fig. 1 D2Q9 model | |
D2Q9 MRT LBM模型时空演化方程为
| $ \begin{array}{*{20}{c}} {{f_\alpha }\left( {r + {e_\alpha }{\delta _t},t + {\delta _t}} \right) = {f_\alpha }\left( {r,t} \right) - \mathit{\boldsymbol{M}}_{il}^{ - 1}{S_{lj}} \times }\\ {\left[ {{m_j} - m_j^{eq}} \right],} \end{array} $ | (1) |
式中:M为将粒子密度分布f映射到m的转换矩阵,即m=Mf,
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{m}} = \mathit{\boldsymbol{M}}f = \left[ {\begin{array}{*{20}{c}} \rho \\ e\\ \varepsilon \\ {{j_x}}\\ {{q_x}}\\ {{j_y}}\\ {{q_y}}\\ {{p_{xx}}}\\ {{p_{xy}}} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} 1&1&1&1&1&1&1&1&1\\ { - 4}&{ - 1}&{ - 1}&{ - 1}&{ - 1}&2&2&2&2\\ 4&{ - 2}&{ - 2}&{ - 2}&{ - 2}&1&1&1&1\\ 0&1&0&{ - 1}&0&1&{ - 1}&{ - 1}&1\\ 0&{ - 2}&0&2&0&1&{ - 1}&{ - 1}&1\\ 0&0&1&0&{ - 1}&1&1&{ - 1}&{ - 1}\\ 0&0&{ - 2}&0&2&1&1&{ - 1}&{ - 1}\\ 0&1&{ - 1}&1&{ - 1}&0&0&0&0\\ 0&0&0&0&0&1&{ - 1}&1&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{f_0}}\\ {{f_1}}\\ {{f_2}}\\ {{f_3}}\\ {{f_4}}\\ {{f_5}}\\ {{f_6}}\\ {{f_7}}\\ {{f_8}} \end{array}} \right].} \end{array} $ | (2) |
其中meq为平衡态速度矩列向量,形式为
| $ {\mathit{\boldsymbol{m}}^{eq}} = \rho {\left[ \begin{array}{l} 1, - 2 + 3\left( {{u^2} + {v^2}} \right),1 - 3\left( {{u^2} + } \right.\\ \left. {{v^2}} \right),u, - u,v, - v,{u^2} - {v^2},uv \end{array} \right]^{\rm{T}}}. $ | (3) |
松弛矩阵S为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{S = }}{\rm{diag}}\left( {{s_0},{s_1},{s_2},{s_3},{s_4},{s_5},{s_6},{s_7},{s_8}} \right)}\\ {\mathit{\boldsymbol{ = }}{\rm{diag}}\left( {{s_0},{s_e},{s_\varepsilon },0,{s_q},0,{s_q},{s_v},{s_v}} \right).} \end{array} $ |
为保证碰撞前后质量和动量守恒, 通常取s0=s3=s5=0;运动黏性不变,取s7=s8=1/τ,s4=s6=8(2τ-1)/(8τ-1),s1,s2取比1略大的数即可,υ=(τ-0.5)Cs2δt。若取s1=s2=s4=s6=s7=s8=1/τ,则回归单松弛时间模型。
粒子平衡分布通常采用如下格式:
| $ f_\alpha ^{\sigma \left( {eq} \right)} = {w_\alpha }{\rho _\sigma }\left[ {1 + \frac{{{e_\alpha } \cdot u_\sigma ^{eq}}}{{C_s^2}} + \frac{{{{\left( {{e_\alpha } \cdot u_\sigma ^{eq}} \right)}^2}}}{{2C_s^4}} - \frac{{u_\sigma ^{eq} \cdot u_\sigma ^{eq}}}{{2C_s^2}}} \right]. $ | (4) |
式中:
本文在进出口采用Zou/He速度入口[11]条件,Zou/He压力出口条件,多孔介质固壁采用半步反弹格式,全流域均采用二阶精度格式。
1.3 渗透率计算由渗透率定义或达西定律变形得
| $ K = \frac{{\mu Q}}{{ - \frac{{{\rm{d}}p}}{{{\rm{d}}x}}A}} = \frac{{\mu \int {\frac{{u{\rm{d}}y}}{A}} }}{{ - \frac{{{\rm{d}}p}}{{{\rm{d}}x}}}}, $ | (5) |
式中:K为渗透率; μ为流体动力黏度; Q为流量; A为截面积,二维多孔介质中取截线长度;
固有渗透率与格点渗透率之间转换关系为Kphysical=KLatticeX2,其中X为格子分辨率,单位为m。
1.4 迂曲度计算多孔介质的迂曲度可以通过对多空介质内稳态时的瞬时速度场[12-13]进行体积平均意义上的估计得出,公式如下
| $ \tau = \frac{{\sum {\sqrt {u_x^2 + u_y^2 + u_z^2} } }}{{\sum {\left| {{u_i}} \right|} }}, $ | (6) |
此处|ui|是i方向上速度分量幅值,i是压降施加方向。
为讨论网格独立性,本文对3.2中R0=22的孔隙结构采用不同网格分辨率去模拟其渗透率。所谓不同分辨率网格指对多孔介质中小圆采用不同分辨率直径,在满足小圆直径和孔喉尺寸比率不变的条件下构成的宏观不同大小的多孔介质网格。对小圆半径采取R=14, 16, 18, 20, 22不同格点数代表,得到不同分辨率的网格。模拟结果见表 1,表中渗透率变化率表明,当R≥18时,对应不同精度网格的多孔体渗透率变化在1%以内,可以认为基本不再变化,故本文取小圆半径R≥18,此时渗透率结果和网格分辨率无关。
|
|
表 1 圆柱半径、网格、渗透率及其变化率 Table 1 Circle diameter, mesh resolution, permeability, and permeability variation |
为检测本文的MRT LBM计算渗透率代码的合理性,首先选取渗透率存在理论解的情形进行验证计算。对于二维细缝平板间的渗透流动,其理论渗透率值为w2/12,w为平行板间距离。取不同板间宽度采用MRT LBM代码进行渗透率计算,其结果和理论计算值相对应,绘制在图 2中,模拟值与真实值误差均在1%以内。

|
Download:
|
| 图 2 二维平行板间渗透率 Fig. 2 Permeability between two parallel plates | |
二维平行板间流域上下板处取半步反弹格式,进口取Zou/He速度入口,出口取Zou/He压力出口,全域二阶精度。
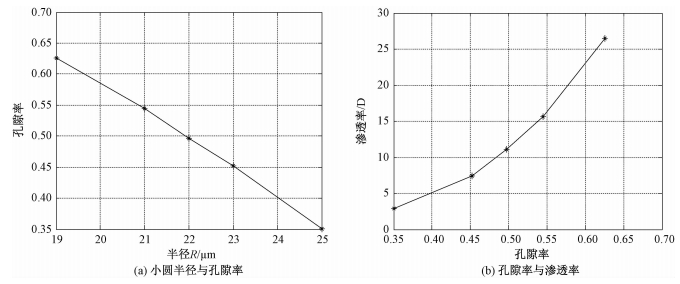
3 二维多孔体孔隙率与渗透率计算结果讨论 3.1 不同孔隙率均匀多孔介质孔隙率与渗透率的关系在550×1 100分辨率的网格上特定位置规则放置不同半径、但数目相同的二维小圆,如3.2中R0=22的孔隙结构,其他不同半径的等径小圆均布形成的多孔体样本在此不再展示。本文生成R=19,21,22,23,25共5个等径小圆均布形成的多孔体样本,R=25时对应孔喉最小,d=5个格子。这5个样本小圆半径、孔隙率、渗透率关系如图 3。图 3(a)结果表明:小圆半径越大,多孔体孔隙率越小。这个结论合理且很容易理解,因为区域大小给定,故骨架占多了,自然孔隙就小,即孔隙率小。
|
Download:
|
| 图 3 等径均布小圆多孔体小圆半径、孔隙率、渗透率关系 Fig. 3 Relations among even distributed circle diameter, porosity, and permeability | |
图 3(b)是均布小圆构成的多孔体孔隙率和渗透率关系,其结果表明:孔隙率越大则渗透率也越大。从几何空间来看,给定空间大小的均布小圆形成的多孔体内,孔隙率越小,孔喉尺寸也就越小,故同样压力梯度下流动越不容易,也就是渗透率越小。可见统计结果与多孔体几何物理特性是完全一致的。
换个角度来看,将R=19的均布小圆多孔体视为原始多孔体,而将半径的增加视为由于流动过程中存在着结垢、盐析或是焦炭结焦等原因产生的均匀流体通道的破坏,从而图 3(b)也可以看成是流动中种种原因造成的均布孔隙率损失和渗透率损失之间的关系,对该结果的进一步分析见表 2。
|
|
表 2 孔隙率损失与渗透率损失关系 Table 2 Porous damage rate and permeability damage rate |
由表 2可以看出,起初孔隙率损失12.92%时,渗透率损失可以达到40.9%,而后面随着沉积物的积累,孔隙率损失在增加,渗透率损失也在增加,渗透率损失稍大于孔隙率损失的2倍,但渗透率损失的边际增加在减少。
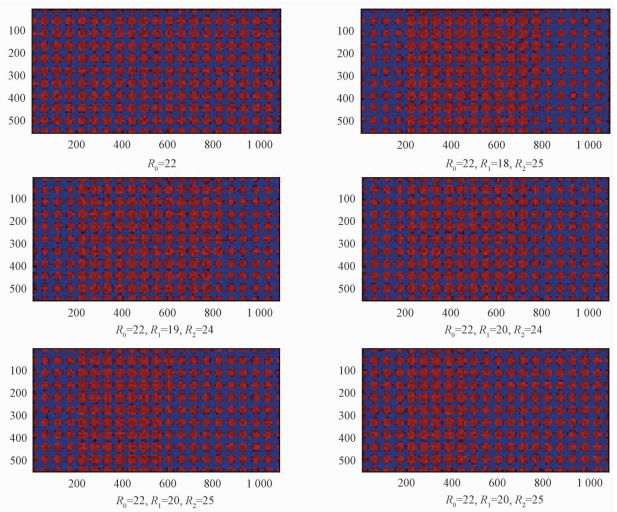
3.2 同孔隙率异构体孔隙结构对渗透率的影响为了考虑同样的孔隙率大小的情况下,不同孔隙分布对多孔体渗透率影响,本文生成如下6个多孔体样本,见图 4。虽然它们在宏观上展现出不同的几何特性,但却具有完全一样的孔隙率0.497,而且孔隙率相等是通过保证同格子尺寸多孔骨架内拥有相同整点个数来实现的,因此是绝对意义上的孔隙率相等。同孔隙率异构的孔隙样本非常多,本文只是选取其中6个二直径小圆组成的同孔隙率异构样本进行探讨。
|
Download:
|
| 图 4 相同孔隙率0.497不同孔隙分布的6个异构多孔体样本 Fig. 4 6 SPDS samples with porosity of 0.497 | |
本文选取的6个样本,孔喉尺寸由最小到最大分别为:5,7,11,13,15,17,19个格子尺寸,本文样本安排同尺寸孔喉分布集中在入口不远的位置。
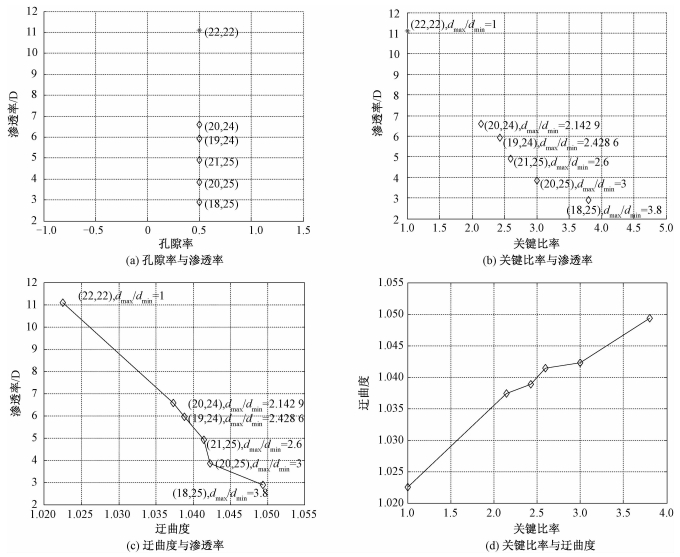
通过对这些样本进行模拟计算,并对结果进行统计,得到同孔隙率异构体孔隙率与渗透率关系如图 5(a)。图中(*)为R=22均布小圆构成孔隙对应的孔隙率和渗透率点。从图中很容易看出,孔隙率相同时,由于孔隙分布不均匀造成的渗透率变化相对于均匀分布样本,最大损失可73.98%,甚至可以达到100%(特殊的、出现死隙、不导通界面的情况)。
|
Download:
|
| 图 5 同孔隙率异构体孔隙率、渗透率、迂曲度、关键比率间关系 Fig. 5 Porosity, permeability, tortuosity, and critical ratio of the SPDS samples | |
表 3是各同孔隙率异构体最大孔喉值、最小孔喉值和最大孔喉最小孔喉比对应关系。为后面讨论方便,本文定义最大孔喉最小孔喉比为关键比率。
|
|
表 3 同孔隙率异构体各样本孔喉参数及关键比率 Table 3 Throat sizes and critical ratios of SPDS samples |
图 5(b)是同孔隙率异构体关键比率与渗透率之间关系,其结果表明,渗透率随关键比率增大而单调变小。这个结论可以从微观孔隙尺度得以印证。关键比率描述的是流通通道的均匀性; 关键比率越接近于1,流道越均匀,宏观渗透率越大; 反之,流道越不均匀,宏观渗透率越小。从孔隙尺度来看,整体多孔体渗透特性不取决于较大孔隙处的渗透特性,而是非常薄的界面层上小孔隙所在处的渗透特性。由此可见,在工程中取少量多孔介质样本,以此样本渗透特性为基础预测传热传质过程的做法缺乏科学依据,应当通过多取一些不同位置的样本、综合评估这些样本的渗透率特性,并以此为基础进行工程预测才比较科学、具有更高的准确性。
图 5(c)是同孔隙率异构体迂曲度和渗透率之间关系,从图中很容易看出,迂曲度越大,渗透率越小,这是非常符合工程实践的。迂曲度大,意味着流体通道曲折蜿蜒,从而流体通过难度加大,也就是渗透率会降低。
图 5(d)是同孔隙率异构体关键比率和迂曲度之间关系,图中结果表明,关键比率越大,迂曲度越大。这点可以通过进一步分析多孔体中几何结构和流场关系得到验证:关键比率越接近1,表明孔隙结构越均匀,流体通道大小越接近,从而产生的速度垂向分量越小,各点速度矢量模值越接近于流道方向速度分量,由公式(6)可知这会导致迂曲度统计值越接近于1;反之,关键比率增大则迂曲度增大。
4 结论本文采用MRT LBM对若干个等径均布圆形成的二维多孔体和二直径圆形成的同孔隙率异构二维多孔体进行数值模拟,探讨其孔隙率和渗透率关系特性及孔隙率损失与渗透率损失关系特性,以及同孔隙率异构体关键比率、迂曲度和渗透率间的关系,本文结论适用于Kn < 0.01,不考虑存在滑移情况下二维或准二维多孔体渗透率特性及渗透率损失估计。
1) 对于一般均匀多孔体,宏观统计孔隙率越大,对应的渗透率也就越大。
2) 当存在着使得孔隙率变小的结垢、沉积、沉降或结焦因素时,若孔隙率损失均匀分布,则由于孔隙率损失带来的渗透率损失率的幅度约为孔隙率损失率的2倍,随着孔隙率损失率的增大,渗透率的边际损失幅度在减小。
3) 同孔隙率异构的多孔体,其各自的渗透率可能会有巨大差异,不取决于流通方向上大孔隙处的渗透率,而是取决于最小孔隙分布界面上的渗透率;孔喉大小越均匀,对应多孔介质渗透率越趋向于最大。
4) 同孔隙率异构多孔体渗透率随关键比率增大而单调减小,随迂曲度增大而单调变小。
5) 同孔隙率异构多孔体迂曲度随关键比率增加而增加。
6) 基于以上原因,实验室内对实际多孔介质在进行工程取样时,要注意多取不同位置的样本进行综合测量、评估,根据对应样本渗透率特性分段对单相流或多相流传热传质过程进行预测,以便可以通过实验结果更精确地指导工程实践。
| [1] |
Ergun S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48:89–94.
|
| [2] |
Carman P C. Flow of gases through porous media[J]. Science, 1956, 124:1254–1255.
DOI:10.1126/science.124.3234.1254 |
| [3] |
Wang J Q, Zhao J F, Zhan Y, et al. Analysis of the effect of particle size on permeability in hydrate-bearing porous media using pore network models combined with CT[J]. Fuel, 2016, 163:34–40.
DOI:10.1016/j.fuel.2015.09.044 |
| [4] |
Gao Y, Zhang X X, Ramae P, et al. Calculating the anisotropic permeability of porous media using the lattice boltzmann method and X-ray computed tomography[J]. Transport Porous Media, 2012, 92:457–472.
DOI:10.1007/s11242-011-9914-7 |
| [5] |
Maarten V. Porosity, permeability and 3D fracture network characterization of dolomite reservoir rock samples[J]. Journal of Petroleum Science and Engineering, 2015, 127:270–285.
DOI:10.1016/j.petrol.2014.12.019 |
| [6] |
查露, 栗晶, 曹传胜, 等. 三维颗粒群沉降的格子Boltzmann模拟[J]. 中国科学院大学学报, 2016, 33(2):240–246.
|
| [7] |
Schaaf S A, Chambre P L. Flow of rarefied gases[M]. Aiche Journal, 2010, 8(3): 293-297.
|
| [8] |
Pan C, Luo L S, Miller CT. An evaluation of lattice boltzmann scheme for porous medium flow simulation[J]. Computers & Fluids, 2006, 35:898–909.
|
| [9] |
Cho H J, Jeong N, Sung H J. Permeability of microscale fibrous porous media using the lattice Boltzmann method[J]. International Journal of Heat and Fluid Flow, 2013, 44:435–443.
DOI:10.1016/j.ijheatfluidflow.2013.07.013 |
| [10] |
Cho H J, Jeong N, Sung H J. Permeability of microscale fibrous porous media using the lattice Boltzmann method[J]. International Journal of Heat & Fluid Flow, 2013, 44(12):435–443.
|
| [11] |
Zou Q, He X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9:1591–1597.
DOI:10.1063/1.869307 |
| [12] |
Ghassemi A, Pak A. Pore scale study of permeability and tortuosity for flow through particulate media using Lattice Boltzmann method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35:886–899.
DOI:10.1002/nag.v35.8 |
| [13] |
Bahman S, Pak A. Numerical investigation of the effects of porosity and tortuosity on soil permeability using coupled three-dimensional discrete-element method and lattice Boltzmann method[J]. Physical Review E, 2015, 91:053301.
DOI:10.1103/PhysRevE.91.053301 |
 2018, Vol. 35
2018, Vol. 35 


