低压环境并耦合加热的水膜蒸发现象常见于海水淡化[1]、材料加工[2-3]以及废物处理[4]等工业过程中。此外,在真空环境中做喷雾冷却时,被冷却表面上形成的液膜的蒸发也是一种典型的低压蒸发现象[5-6]。水膜的蒸发相变过程成为上述工业或工艺过程中的主要影响因素,理解和掌握水膜低压蒸发相变的特性和机理,对于优化相关工艺过程、提高生产效益具有重要意义。
水蒸发导致系统质量和温度的变化本质上是气-液界面分子扩散行为的宏观结果。经典的蒸发-凝结理论认为气-液界面分子的扩散行为同时包含分子向空间的蒸发逃逸行为和向液面的凝结回落行为[7]。当前者的质量流率大于后者,表现为宏观的蒸发现象;反之,表现为宏观的凝结现象。研究人员采用分子动力学模拟的方法尝试从微观角度揭示界面分子的扩散行为[8],发现在气液平衡体系中界面附近存在局域热非平衡区域,获得了界面碰撞分子停留在液相区的分子数目随时间的变化规律。实验研究发现,极低压条件水蒸发在界面处存在温度的跳跃性变化[9]。斐克扩散定律[10]从存在于界面的浓度梯度的角度对蒸发现象进行机理描述,为研究流体的蒸发扩散特性提供了理论基础。本文基于斐克扩散定律,理论结合实验研究低压封闭腔内水膜蒸发的一般特性。
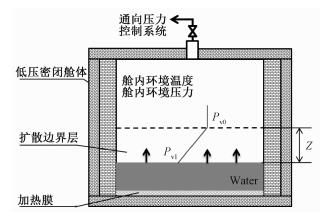
1 蒸发模型低压密闭舱体内水膜蒸发过程示意图如图 1所示。假设初始时刻舱体内水蒸气分压力为零,水膜的蒸发使得舱体内的压力升高,为了维持舱体内的恒压环境,需要将部分含有水蒸气的空气排出舱体。在上述过程中,水膜逐渐从不饱和状态变化到饱和状态,本文正是关注该过程中水膜的蒸发特性。模型构建依据的假设条件为:1)低压舱体密闭且绝热;2)在低压环境中将空气和蒸气视为理想气体;3)由于加热热流密度和液膜厚度较小,不考虑液膜内部的温度不均匀性和气泡对蒸发的影响。
|
Download:
|
| 图 1 密闭腔体内水膜加热蒸发物理模型 Fig. 1 Model of water film heating evaporation in a closed cabin | |
密闭舱体内的总压Ptot为空气压力Pa和水蒸气压力Pv之和,表示为
| $ {P_{{\rm{tot}}}} = {P_{\rm{a}}} + {P_{\rm{v}}}, $ | (1) |
其中,水蒸气分压力Pv为
| $ {P_{\rm{v}}} = RH\cdot{P_{{\rm{sat}}}}, $ | (2) |
式中:RH为相对湿度,Psat为饱和水蒸气压力,计算式为
| $ {P_{{\rm{sat}}}} = 8.953 \times {10^5}{\rm{EXP}}\left\{ {- {{\left[{\frac{{\left( {T + 49.05} \right)}}{{84.05}}} \right]}^2}} \right\}, $ | (3) |
式中T表示水膜温度。
根据斐克定律,水膜蒸发速率的计算式为
| $ \frac{{{\rm{d}}{m_{\rm{e}}}}}{{{\rm{d}}\tau }} =-A{D_{{\rm{diff}}}}\frac{{{M_{\rm{w}}}}}{{R{T_{\rm{a}}}}}\frac{{\partial {P_{\rm{v}}}}}{{\partial z}}, $ | (4) |
式中:me为蒸发质量;τ为时间;A为蒸发面积;R为通用气体常数(8.314 J/(mol·K));Ta为气体温度;Ddiff为扩散系数[10],计算式为
| $ {D_{{\rm{diff}}}} = 1.87 \times {10^{-10}}\left( {\frac{{{T^{2.072}}}}{p}} \right), $ | (5) |
式中:p以大气压(atm)为单位,该式的适用范围为282 K≤T≤450 K。系统的温度变化可根据热量守恒求得:
| $ ({m_{\rm{w}}}{c_{{\rm{pw}}}} + {m_{\rm{a}}}{c_{{\rm{pa}}}}){\rm{d}}T = qA{\rm{d}}\tau-{m_{\rm{e}}}{h_{{\rm{lt}}}}, $ | (6) |
式中: mw和ma分别为舱体内水膜和空气质量;cpw和cpa分别为水和空气的比热容; q指提供的热流; hlt指水的气化潜热。式(4)中∂Pv/∂z为扩散边界层内蒸汽压力梯度,其中z表示扩散边界层厚度,如图 1所示,其计算方法见本文第2节。
舱体内空气摩尔数na和水蒸气组分摩尔数nwv分别表示为:
| $ {n_{\rm{a}}} = {P_{\rm{a}}}V/R{T_{\rm{a}}}, $ | (7) |
| $ {n_{{\rm{wv}}}} = {P_{\rm{v}}}V/R{T_{\rm{a}}} + \Delta {n_{{\rm{wv}}}}. $ | (8) |
式中:V表示蒸发腔体体积;Δnwv为由水膜蒸发导致的水蒸气物质的量增量,计算式为
| $ \Delta {n_{{\rm{wv}}}} = \Delta {m_{\rm{e}}}/{M_{\rm{w}}}, $ | (9) |
式中Mw为水分子摩尔质量。
在水膜蒸发过程中,为维持舱体压力恒定,需要时时排出一定量的气体。计算过程中,一个时间步长内的排气量为
| $ n_{_{{\rm{ext}}}}^{^i} = n_{_{{\rm{tot}}}}^{^{i + 1}}-n_{_{{\rm{tot}}}}^{^i}({T^i}/{T^{i + 1}}), $ | (10) |
式中:next和ntot分别为所排气体和舱内气体总的物质的量;上标i和i+1指迭代计算过程中的时间步。获得排出气体的物质的量next后,可分别求出排出水蒸气的物质的量nwv_r和空气的物质的量na_r,分别为:
| $ n_{_{{\rm{wv\_r}}}}^{^i} = n_{_{{\rm{ext}}}}^{^i}(n_{_{{\rm{wv}}}}^{^i} + \Delta n_{_{{\rm{wv}}}}^{^i})/n_{_{{\rm{tot}}}}^{^{i + 1}}, $ | (11) |
| $ n_{_{{\rm{a\_r}}}}^{^i} = n_{_{{\rm{ext}}}}^{^i}n_{\rm{a}}^{^i}/n_{_{{\rm{tot}}}}^{^{i + 1}}. $ | (12) |
从方程(4)可以看出,扩散边界层厚度z的取值大小直接影响水膜蒸发速率的计算结果;但是,影响z值的因素较多,至今还没有一个理论或经验公式能够准确预测z值大小。在假定z值大小一定的情况下,迭代求解方程(4)和方程(6)发现,当z取值不同时,水膜最终的平衡温度也是不同的。当z取值较大时,水膜的平衡温度相对较高;反之,当z取值较小时,水膜的平衡温度相对较低。当水膜达到饱和状态(实验观察有气泡不断产生)时,则水膜的平衡温度一定等于舱体环境压力对应的水饱和温度。基于上述分析并结合实验研究,给水膜足够大的加热功率使水膜达到饱和沸腾状态。将实验过程的条件作为模型迭代求解的初始条件和边界条件,改变z值大小获得不同的水膜平衡温度,当水膜的平衡温度等于该压力条件下水膜的饱和温度时,则该条件下的z值即为该压力条件下水膜扩散边界层厚度。列举实例:假设环境压力为1.8 kPa,水膜质量和初始温度分别为0.02 kg和9.5 ℃,加热功率为376 W/m2,蒸发面积为19.5 cm2,环境的初始相对湿度为20%,赋值z分别为3,7和14 mm。计算结果如图 2所示,可以看出,对应z=3,7和14 mm时水膜的平衡温度分别为15.3,16和17.1 ℃。但由于计算选取的环境压力为1.8 kPa,该压力对应的饱和温度为16 ℃,因此,认为扩散边界层厚度为z=7 mm。从后面的实例中还可以看出,利用该方法确定的z值代入模型后获得的水膜蒸发质量和温度的预测值与实验结果的吻合程度较高。

|
Download:
|
| 图 2 在不同蒸发厚度水膜温度变化 Fig. 2 Changes in temperature of water film at different depths of diffusion boundary layer | |
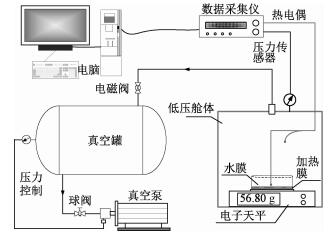
实验系统如图 3所示,主要由真空泵、真空缓冲罐、真空舱体和数据采集系统组成。其中,真空泵的抽气速率为15 L/s,真空缓冲罐的体积为400 L,真空舱体的尺寸为350 mm×250 mm×250 mm。使用精密电子天平测量水膜的蒸发量,测量精度为0.01 g。真空舱体压力采用压力传感器测量,量程为0~400 mbar,测量精度为0.05%。其他参数同2节所述。
|
Download:
|
| 图 3 水膜低压蒸发实验系统 Fig. 3 Experimental system of water film vaporization under low pressure | |
实验开始前,将一定质量和温度的水放入含有加热片的蒸发器皿中;关闭真空舱体和缓冲罐之间的连结阀门,启动真空泵将缓冲罐抽至某一低压值;缓慢开启真空舱体和缓冲罐之间的连结阀门,直至真空舱体内的压力降至恒定的目标压力后,关闭连结阀门;开启电加热,时时记录水温变化,实验持续时间为7 200 s,间隔一段时间记录水膜质量变化;当舱体压力升高时,缓慢开启连结阀门,抽出多余气体,恢复舱体压力至目标值。实验过程的其他参数将在数据结果的具体讨论中给出。
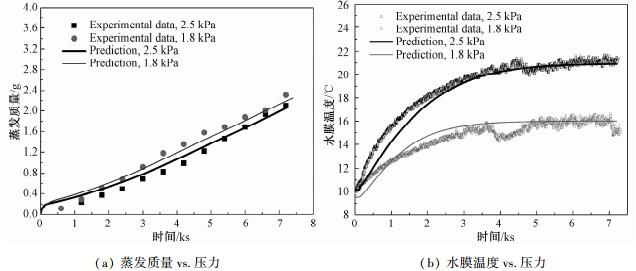
4 模型验证图 4展示水膜蒸发质量和温度随时间变化的实验结果和计算结果的对比,其中图中的实验结果均为多次测量后的平均结果。从图中可以看出,两种条件下蒸发质量/水膜温度的实验结果和计算结果的数值和分布趋势吻合程度比较高。7 200 s,舱体压力为2.5 kPa时水膜的蒸发质量为2.04 g,舱体压力为1.8 kPa时水膜的蒸发质量为2.18 g。从水膜温度的变化曲线图中看出,两种条件下水膜温度的实验结果和计算结果的分布趋势吻合度较高,最大误差约±1 ℃。值得注意的是压力为1.8 kPa时,实验结果在3 500~4 000 s之间时下降约1 ℃,之后在5 000 s时又缓慢恢复至饱和温度16 ℃。在多次的反复实验中均出现这种温度的波动现象,实验观察中有气泡附着在热电偶表面,这可能是由于水膜内部气泡的扰流-破裂造成的。
|
Download:
|
| 图 4 不同压力条件下水膜蒸发质量和温度变化 Fig. 4 Variations in water film evaporation mass and temperature under different low pressures | |
图 5为不同压力和加热功率条件下水膜的蒸发速率和水蒸气分压力随时间的分布变化,其中舱体压力分别为1.8和2.5 kPa,加热功率分别为376和485 W/m2。从图中可看出,在开始的前300 s内,水膜的蒸发速率从1.1~1.4 g/(m2·s)快速降至0.1 g/(m2·s),降幅达一个量级,之后缓慢小幅回升至一恒定水平(≤0.2 g·m-2·s-1)。这是因为初始时刻封闭空间内没有水蒸气,即水蒸气的分压力为零,水膜表面的蒸汽扩散压力或水蒸气的压力梯度最大,因此,计算开始时获得的水蒸气扩散速率也最大。随着水蒸气的扩散,密闭舱内的水蒸气分压力迅速增大,导致水膜表面的水蒸气压力梯度不断减小,密闭舱内的水蒸气扩散速率快速下降。当密闭舱内充满水蒸气后,水膜蒸发速率接近一恒定数值,该数值大小取决于水膜的加热功率。对比图中曲线分布可以看出,压力越小或加热功率越大,水膜的蒸发速率越大。值得注意的是,约在4 000 s和5 000 s之后,蒸发速率曲线出现重合现象。结合水蒸气的分压力曲线不难看出,此时水膜已经达到饱和状态。当水膜处于饱和状态时,加热热流完全转化为水的汽化潜热,加热功率越大,水膜的汽化速率越大。从水蒸气的分压力曲线可以看出,与蒸发速率的分布趋势相反,蒸汽分压力在前300 s内近似直线上升至某一水平(约1 200 Pa),之后缓慢增大至饱和压力水平。与预期相同,加热功率越大或压力越小,蒸汽分压力达到饱和压力的时间越短。

|
Download:
|
| 图 5 压力、加热功率对水膜蒸发速率和舱内水蒸气的分压力影响 Fig. 5 Effects of pressure and heating power on water film evaporation rate and water vapor partial pressure | |
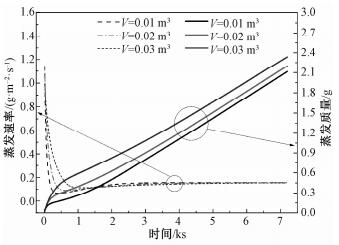
图 6为不同低压舱体容积对水膜蒸发速率和蒸发质量的影响,与图 5中蒸发速率曲线分布趋势相似,蒸发速率快速大幅降低,然后稳定于某一恒定水平,约0.12 g·m-2·s-1。当其他条件不变,单纯改变蒸发容积大小,并不能提高稳定时的蒸发速率,但是相同时间内的蒸发量随着蒸发容积的增大而增大。
|
Download:
|
| 图 6 舱体容积对水膜蒸发质量和蒸发速率的影响(q=376 W/m2) Fig. 6 Effect of cabin volume on water film evaporation mass and rate | |
针对低压加热条件下密闭舱体内的水膜蒸发,建立一维蒸发模型,提出一种水膜扩散边界层厚度的计算方法,实现了模型的封闭求解。开展相关的实验研究,对模型的预测性能进行验证。获得以下主要结论:
1) 在本文条件下,水膜蒸发质量、温度的计算结果和实验结果吻合程度较高,表明该模型能够应用于实际的工业工程中,实现低压加热环境中液膜的蒸发特性预测。
2) 加热表面水膜的蒸发速率受舱体体积、加热功率和环境压力等多种因素的影响。在本文条件下,水膜蒸发速率表现出快速下降-缓慢回升-平稳分布的趋势。稳定之后的蒸发速率取决于加热功率的大小。
3) 舱体压力越小或加热功率越大,蒸气分压力达到饱和压力的时间越短;蒸发容积越大,相同时间内水膜的蒸发质量越大,但达到饱和蒸发状态时的蒸发速率相同。
| [1] |
陈学, 刘晓华, 沈胜强, 等. 水平管外降膜蒸发传热实验研究[J]. 太阳能学报, 2015, 36(8):1996–2001.
|
| [2] |
Liu L, Wang Y, Fan D, et al. Using phenolphthalein as a promising indicator to monitor the vacuum freeze-drying process[J]. Materials Letters, 2015, 139:245–248.
DOI:10.1016/j.matlet.2014.10.047 |
| [3] |
Bai Y, Pang C, Hu W, et al. High capacity cobalt boride prepared via vacuum freeze-drying method and used as anode material for alkaline secondary battery[J]. Journal of Renewable and Sustainable Energy, 2013, 5(2):021401.
DOI:10.1063/1.4798422 |
| [4] |
Wheeler R R, Hadley N M, Dahl R W, et al. Microwave enhanced freeze drying of solid waste[R]. SAE Technical Paper, 2007.
|
| [5] |
Cheng W, Chen H, Hu L, et al. Effect of droplet flash evaporation on vacuum flash evaporation cooling:modeling[J]. International Journal of Heat and Mass Transfer, 2015, 84:149–157.
DOI:10.1016/j.ijheatmasstransfer.2014.12.078 |
| [6] |
Wang C, Xu R, Song Y, et al. Study on water droplet flash evaporation in vacuum spray cooling[J]. International Journal of Heat and Mass Transfer, 2017, 112:279–288.
DOI:10.1016/j.ijheatmasstransfer.2017.04.111 |
| [7] |
Cammenga H K. Evaporation mechanisms of liquids[J]. Current topics in materials science, 1980, 5:335–446.
|
| [8] |
王遵敬. 蒸发与凝结现象的分子动力学研究及实验[D]. 北京: 清华大学, 2002.
http://d.wanfangdata.com.cn/Thesis/Y815850 |
| [9] |
肖宁, 赵小明, 陈民, 等. 液体蒸发率及表面温度测量[J]. 工程热物理学报, 2007, 28(5):748–750.
|
| [10] |
Lienhard J H.
A heat transfer textbook[M].4th ed. New York: Courier Corpora, 2013.
|
 2018, Vol. 35
2018, Vol. 35 


