2. 中国科学院大学, 北京 100190
2. University of Chinese Academy of Sciences, Beijing 100190, China
SM4[1]算法即原SMS4算法,是由国家密码管理局于2006年公布的用于无线局域网产品的分组密码算法。SM4密码算法是国内官方公布的第一个商用密码算法,并于2012年3月被国家密码管理局批准为行业标准[2]。目前国内应用在安全产品(如IPSec VPN、SSL、TLS等)上的密码算法正逐步使用SM4算法取代DES[3]。
市场上的安全产品对使用的密码算法有较高的软件实现性能要求。截至目前,国内外学者对SM4软件优化实现方面关注度较小,SM4的软件实现方法仅限于查表实现。受限于SM4算法的设计等因素,SM4采用查表方法的软件实现性能明显落后于AES[4]的查表实现。此外,2008年3月Intel、AMD处理器厂商宣布在其x86架构处理器上推出用于AES加/解密运算的AES-NI指令集[5]。采用AES-NI指令集实现AES算法的软件实现性能是采用查表方法实现SM4的4.23倍。因此,SM4算法的快速软件实现技术成为重要研究内容。
近些年,国内外许多学者尝试将采用SIMD技术的SSE/AVX指令[6]应用到密码算法的软件实现上。SIMD的全称是“Single Instruction Multiple Data”,即单指令多数据。该技术可实现同一操作并行处理多组数据。SIMD技术最大的优点在于它的并行性。2012年,Seiichi和shiho[7]利用SSE指令结合bit-slice技术[8]应用到PRESENT[9]、Piccolo[10],使二者的实现吞吐量分别达到4.73和4.57 cycle/byte。2013年,Neves和Aumasson[11]利用AVX2指令应用到SHA-3候选算法BLAKE[12]上并提高了其实现性能。但是,截至目前,高端处理器(如Intel Core i7等)上的国产密码SM4优化实现方面的工作尚没有公开发表。
本文探讨SM4算法在x86架构处理器上的软件优化实现方法。将SIMD技术的并行性应用到SM4的软件优化实现当中。实验结果表明,与目前基于查表的方法相比, SM4采用SIMD技术的软件实现性能有明显优势。
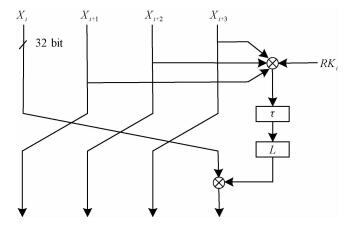
1 SM4算法简介SM4是一个分组密码算法,分组长度及主密钥长度均为128 bit。128 bit主密钥经密钥编排算法扩展为32个32-bit轮子密钥,加/解密变换均为32轮轮函数F的迭代。轮函数F的结构如图 1所示。
|
Download:
|
| 图 1 SM4轮函数F结构图 Fig. 1 Structure of SM4 round function F | |
设明文输入为(X0, X1, X2, X3)∈(Z232)4,密文输出为(Y0, Y1, Y2, Y3)∈(Z232)4,轮密钥为RKi∈ Z232,i=0, 1, …, 31. SM4的加密变换为
| $ \begin{array}{l} {X_{i + }}{_4} = F{\rm{ }}({X_i}, {X_{i + }}{_1}, {X_{i + }}{_2}, {X_{i + }}{_3}, R{K_i}) = {X_i} \oplus \\ T{\rm{ }}({X_{i + }}{_1} \oplus {X_{i + }}{_2} \oplus {X_{i + }}{_3} \oplus R{K_i}), i = 0, 1, \cdots, 31. \end{array} $ | (1) |
密文(Y0, Y1, Y2, Y3)=(X35, X34, X33, X32)。SM4算法的解密变换与加密变换结构相同,不同的仅是轮密钥的使用顺序(解密过程将加密过程轮密钥的使用顺序颠倒即可)。
式(1)中T变换操作是由非线性变换τ和线性变换L复合而成,即T(·)=L(τ(·))。该变换是一个Z232→Z232的可逆变换。
非线性变换τ:τ是由4个8 bit S盒操作并置构成。将τ的输入记为A=(a0, a1, a2, a3)∈(Z28)4,输出B=(b0, b1, b2, b3)∈(Z28)4,非线性变换τ可定义为
| $ B = \tau \left( A \right) = (Sbox{\rm{ }}({a_0}), Sbox{\rm{ }}({a_1}), Sbox{\rm{ }}({a_2}), Sbox{\rm{ }}({a_3})). $ |
线性变换L:τ的输出是线性变换L的输入。设输入为B∈Z232,输出为C∈Z232,线性变换L可定义为
| $ CC = L\left( B \right) = B \oplus \left( {B \lll 2} \right) \oplus \left( {B \lll 10} \right) \oplus \left( {B \lll 18} \right) \oplus \left( {B \lll 24} \right). $ |
查表实现是密码算法软件实现的最基本方法,该方法是Daemen和Rijmen[4]在32-bit处理器上实现Rijndael时提出的。他们将Rijndael轮变换操作制成4个8-bit输入32-bit输出的表,一轮Rijndael可通过16次查表实现[4]。查表方法的核心思想是将密码算法轮函数中尽可能多的变换操作制成表。
SM4加/解密轮函数中的T变换由非线性变换τ和线性变换L构成。将非线性变换τ的输入记为X=(x0, x1, x2, x3)∈(Z28)4,输出记为Y=(y0, y1, y2, y3)∈(Z28)4。可将非线性变换τ的操作定义如下。
| $ {y_i} = Sbox{\rm{ }}\left( {{x_i}} \right), 0{\rm{ }} \le {\rm{ }}i < {\rm{ }}4. $ | (2) |
将线性变换L的输入记为P=(p0, p1, …, pn-1)∈(Z2m)4,输出记为Q=(q0, q1, …, qn-1)∈(Z2m)4。其中,m大小需为SM4使用S盒规模的倍数,m与n的关系满足n=32/m。由于L中仅包含循环移位和异或操作。因此,可将线性变换L的操作定义为式(3),非线性变换T操作可由式(2)与式(3)合并表示为式(4):
| $ Q = L\left( B \right) = L{\rm{ }}\left( {{p_0} \ll \left( {n-1} \right){\rm{ }}m} \right) \oplus L{\rm{ }}({p_1} \ll \left( {n-2} \right){\rm{ }}m) \oplus \cdots \oplus L{\rm{ }}({p_n}{_{-1}}). $ | (3) |
| $ \begin{array}{l} Q = T\left( X \right) = L\left( {Sbox{\rm{ }}\left( {{x_0}} \right) \ll \left( {n-1} \right){\rm{ }}m} \right) \oplus L\\ \left( {Sbox{\rm{ }}\left( {{x_1}} \right) \ll \left( {n-2} \right){\rm{ }}m} \right) \oplus \cdots \oplus L(Sbox{\rm{ }}({x_n}{_{-1}})). \end{array} $ | (4) |
由式(4)可知,可将非线性变换T的操作制成n个m-bit输入32-bit输出的表:
1) 当m=8时,4个8-bit输入32-bit输出的制表操作如下:
| $ \begin{array}{l} {\rm{T}}3[{d_0}] = L(Sbox{\rm{ }}({d_0}) \ll 24);\\ {\rm{T}}2[{d_1}] = L(Sbox{\rm{ }}({d_1}) \ll 16);\\ {\rm{T}}1[{d_2}] = L(Sbox{\rm{ }}({d_2}) \ll 8);\\ {\rm{T}}0[{d_3}\left] { = L\left( {Sbox{\rm{ }}\left( {{d_3}} \right)} \right);{d_i} \in } \right[0, 255], 0 \le i < 4。\end{array} $ |
2) 当m=16时,2个16-bit输入32-bit输出的制表操作如下:
| $ \begin{array}{l} {\rm{T}}1[{d_0}] = L(Sbox{\rm{ }}\left( {{d_0} \gg 8} \right)||Sbox{\rm{ }}({d_0}\& 0{\rm{x00ff}}));\\ {\rm{T}}0[{d_1}] = L(Sbox{\rm{ }}\left( {{d_1} \gg 8} \right)||Sbox{\rm{ }}({d_1}\& 0{\rm{x00f}}f));\\ {d_i} \in \left[{0, 65535} \right], 0 \le i < 4. \end{array} $ |
因此,T变换操作可通过查表方法实现,T变换操作的伪代码实现如下所示:
|
|
表大小权衡:对于查表方法,轮函数变换是通过使用移位、掩码、查表和异或操作实现。这些操作的数量取决于表的大小(每个表的大小ST=2m×4 bytes),即选取m的大小对查表实现有直接的影响。实际上,m越大,轮函数变换所需的操作数量越少,但是这样会增加轮函数中查表操作的延时。结合Ryad等[13]提出的“cache latency”模型,并通过实验验证, m值为8时,SM4查表方法实现性能最佳。
3 SM4 SIMD技术并行实现本文提升SM4的软件实现性能的途径是使用SIMD技术并行实现。一般来说,并行分为细粒度并行和粗粒度并行2种。前者是一组消息在密码算法内部并行处理,这种方式取决于密码算法的设计。如Neves和Aumasson[11]对SHA-3候选算法BLAKE使用SIMD技术优化便是采用细粒度并行策略。而后者是多组消息的并行处理,分组密码通常是在某种工作模式下加/解密大量数据,在特定的工作模式(如ECB、CTR、GCM、CBC(解密方向))下分组密码可并行处理多组消息。由于SM4算法不适合使用细粒度并行,因此,本文选取粗粒度并行策略实现SM4。
3.1 SIMD技术指令集概述SIMD技术可实现同一操作并行处理多组数据。目前支持SIMD技术的处理器厂商主要有Intel、AMD、ARM等。Intel处理器中的SSE/AVX指令集及AMD处理器中的SSE/XOP指令集中的指令均采用SIMD技术。目前,大多数PC及服务器采用的是Intel处理器。下面就应用到SM4并行实现上的AVX2指令集作简要介绍。
3.1.1 AVX2指令集简介2008年Intel宣布推出“Advanced Vector Extensions”(AVX),引入256-bit宽向量指令集。相比于在128-bit SIMD寄存器——xmm上操作的SSE指令集,AVX指令集有如下改进:1)处理的数据量由128-bit扩展为256-bit;2)消除从内存存取数据时对内存对齐的约束;3)实现非破坏性操作,指令的操作数由2个扩展为3个,2个源操作数的计算结果存放到单独的目的操作数中。AVX指令操作对象称为ymm的256-bit SIMD寄存器(AVX指令操作也支持128-bit SIMD寄存器),该寄存器内容分为2个128-bit lanes。AVX指令操作对象为lanes,该指令不支持跨越lanes的操作。
2011年Intel发布AVX2指令集,该指令集是对AVX的扩展和改进,AVX2指令支持跨越lanes的操作。AVX2支持8道32-bit整数异或(vpxor)、移位(vpslld)、置换(vpermd)、查表(vpgatherdd)等,这些SIMD指令可应用于SM4实现。2013年Intel在22 nm Haswell微架构处理器上正式推出AVX2指令集。
3.1.2 相关AVX2指令本小节关注应用于SM4实现的一些AVX2指令,简要介绍每个AVX2指令的功能。为了更好地理解和使用SSE/AVX指令集,目前主流编译器厂商如Intel、GCC、Microsoft Visual C++等均支持SSE/AVX指令的C/C++接口,该接口经编译后映射为SSE/AVX指令。表 1总结了本文实现SM4使用的AVX2指令及对应的C/C++接口。
|
|
表 1 用于实现SM4的AVX2指令 Table 1 AVX2 instructions used for implementation of SM4 |
ARX SIMD:使用AVX2实现“add-rotate-xor”(ARX),可以使用以下指令:8道32-bit整数加指令vpaddd、4道64-bit整数加指令vpaddq;256-bit异或指令vpxor;32-、64-bit逻辑左右移指令vpslld、vpsrld、vpsllq、vpsrlq。
vpshufb:AVX2中的vpshufb指令继承了SSE指令集中的字节置换指令pshufb。vpshufb指令需要2个xmm寄存器作为输入,如图 2中的xmm0和xmm1。目的操作数xmm0中16个字节的置换结果取决于xmm1:xmm1中每个字节低位nibble值作为“置换掩码”选取xmm0中某一位置的字节。如图 2执行指令“pshufb xmm0, xmm1”,xmm1中第9个字节0x10=16,xmm0第9个字节内容为置换前xmm0的第0个字节。当xmm1中某一字节内容大于127时,对应xmm0字节位置内容被置为0。

|
Download:
|
| 图 2 vpshufb指令执行 Fig. 2 Execution of vpshufb instruction | |
向量查表指令:vpgatherdd指令是AVX2扩展AVX最重要的指令之一,该指令可实现4/8道32-bit字并行查表。vpgatherdd指令的具体功能可用如下代码表示:
|
|
本节详细阐述使用SIMD技术的AVX2指令并行实现SM4的过程方法。AVX2指令使用128-bit xmm寄存器可实现4组消息的并行加/解密,使用256-bit ymm寄存器可实现8组消息的并行加/解密。接下来首先说明SM4并行实现时的消息存储格式。
3.2.1 SM4消息存储格式将n组128-bit SM4明文消息记为Pi (0 ≤ i < n, n=4, 8)。需将Pi装载到4个SIMD寄存器R0、R1、R2、R3中。装载规则如下
| $ {R_k}\left[i \right] \leftarrow {P_i}\left[k \right], 0 \le i < n, 0 \le k < 4, $ |
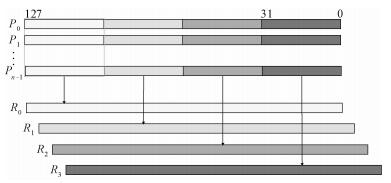
其中,Rk[i]表示Rk寄存器中第i个32-bit字位置,Pi[k]表示明文消息Pi中第k个32-bit字的内容。即Rk寄存器依次存储着所有n组明文消息的第k个32-bit字内容。如图 3所示。
|
Download:
|
| 图 3 SM4明文消息装载格式 Fig. 3 Plaintext message format of SM4 | |
如3.1.2节所述,AVX2指令支持4/8道32-bit字向量查表操作,因此装载n组SM4明文消息可通过向量查表指令vpgatherdd完成。代码如下所示:
|
|
SM4轮函数中包含轮密钥层变换,因此为实现n组消息并行加/解密须将n个32-bit轮密钥装载到SIMD寄存器中。将32个轮密钥装载到SIMD寄存器有2种方式:1)每次轮变换时使用AVX2指令vpgatherdd装载到SIMD寄存器中;2)进入SM4加/解密操作前,依次将32个轮密钥存放在SIMD寄存器中。受限于Intel、AMD处理器中只有16个SIMD寄存器,本文采用第1种方式。实现装载轮密钥的代码如下。
|
|
SM4轮函数中的T变换操作是由非线性变换τ和线性变换L复合而成。并行实现T变换有2种策略:1)分别实现τ和L;2)将τ和L合并实现。接下来分别阐述这2种策略的实现方法。
策略1:T变换中的τ是由4个S盒操作并置构成。SM4所使用的S盒规模为8-bit。不同于轻量级密码所使用的4-bit S盒可通过vpshufb指令实现[13]。但是,可将8-bit的S盒输出规模转换为32-bit,借助AVX2的vpgatherdd指令即可实现SM4 S盒操作。将8-bit S盒输出规模转换为32-bit有2种方法:1)将8-bit S盒转换为4个8-bit输入32-bit输出表;2) 8-bit S盒转换为2个16-bit输入32-bit输出表。
1) 方法1
将SM4的S盒表记为ST,转换后的4个表记为S0、S1,S2、S3。S0-S3的生成规则如下:
| $ \begin{array}{l} S0\left[i \right] = ST\left[i \right];\\ S1\left[i \right] = ST\left[i \right] \ll 8;\\ S2\left[i \right] = ST\left[i \right] \ll 16;\\ S3\left[i \right] = ST\left[i \right] \ll 24;0 \le i < 256. \end{array} $ |
因此,非线性变换τ即可通过掩码、移位、异或、查表操作实现。如式(5)所示。
| $ \begin{array}{l} \tau \left( R \right) = S0[R\& {\rm{0xff}}] \oplus S1\left[{\left( {R \gg 8} \right)\& {\rm{0xff}}} \right]\\ \oplus S2\left[{\left( {R \gg 16} \right)\& 0{\rm{xff}}} \right] \oplus {\rm{ }}S3\left[{R \gg 24} \right]. \end{array} $ | (5) |
式(5)使用AVX2指令实现如下所示:
|
|
|
|
2) 方法2
将SM4的S盒表记为ST,转换后的2个表记为S0、S1。S0、S1的生成规则如下:
| $ \begin{array}{l} S0\left[{256i + j} \right] = \left( {ST\left[i \right] \ll 8} \right) \oplus ST\left[j \right];\\ S1\left[{256i + j} \right] = \left( {\left( {ST\left[i \right] \ll 8} \right) \oplus ST\left[j \right]} \right) \ll 16;\\ 0 \le i < 256, 0 \le j < 256. \end{array} $ |
因此,非线性变换τ即可通过掩码、移位、异或、查表操作实现。如式(6)所示。
| $ \tau \left( R \right) = S0[R\& {\rm{0xffff}}\left] { \oplus S1} \right[\left( {R \gg 16} \right)\& 0{\rm{xffff}}]. $ | (6) |
式(6)使用AVX2指令实现如下所示:
|
|
T变换中的L包含循环移位和异或操作,一般来说,循环移位操作可通过左移、右移和异或操作实现。经研究发现,可使用字节置换指令vpshufb优化L中包含的4个循环移位操作:
1)
2)
3)
因此,完成线性变换L中包含的循环移位操作只需执行1次左移vpslld、1次右移vpsrld、1次异或vpxor、3次字节置换vpshufb共6条AVX2指令即可。
策略2:如第3节所述,SM4中T变换包含的非线性变换τ与线性变换L合并后可制成:1) 4个8-bit输入32-bit输出;2) 2个16-bit输入32-bit输出的表。如前所述,对于输出规模为32-bit的表,可使用AVX2中的vpgatherdd指令实现并行查表。
1) 8-bit输入32-bit输出查表实现
将T变换制成的4个表记为T0、T1、T2、T3。这样T变换即可通过掩码、异或、移位、查表操作实现。如式(7)所示。
| $ \begin{array}{l} T\left( R \right) = T0[R\& 0{\rm{xff}}] \oplus T1[\left( {R \gg 8} \right)\& 0{\rm{xff}}]\\ \oplus T2[\left( {R \gg 16} \right)\& {\rm{0xff}}\left] { \oplus T3} \right[R \gg 24]. \end{array} $ | (7) |
2) 16-bit输入32-bit输出查表实现
将T变换制成的2个表记为T0、T1。这样T变换即可通过掩码、异或、移位、查表操作实现。如式(8)所示:
| $ T\left( R \right) = T0[R\& {\rm{0xffff}}] \oplus T1[\left( {R \gg 16} \right)\& 0{\rm{xffff}}]. $ | (8) |
式(7),式(8)的AVX2指令实现方式分别与式(5),式(6)类似。
总结:对比上述2种策略的实现方法,发现策略2的实现方法与策略1中非线性变换τ的实现方法相比,除所使用的表中数据不同外,其他完全相同。但是,在策略1的实现中还包含线性变换L的实现过程。经实验验证,策略2优于策略1所使用的方法。因此,本文采用策略2中描述的实现方法。
3.2.4 轮函数F优化本节简要介绍SM4轮函数F实现中的优化技巧。3.2.1节中使用4个SIMD寄存器R0、R1、R2、R3存储n组消息。由图 1结合式(1)可知,轮函数F中T变换的输入是3个32-bit消息与轮密钥异或的结果,该结果需要存储在临时寄存器中。如3.2.2节所述,在每轮轮函数变换中均要将轮密钥从内存装载到SIMD寄存器中,因此可将存储轮密钥的SIMD寄存器R4作为该临时寄存器存储T变换的输入。此外,由图 1可知,SM4的轮函数F有如下规律:第1、2、3位置的32-bit字R1、R2、R3和轮密钥R4经过T变换后异或并更新第0位置的32-bit字R0,然后4个32-bit字循环左移一个32-bit位置作为下一轮的输入。循环移位32-bit通过调整SIMD寄存器的顺序即可,如轮函数F的输入为R0、R1、R2、R3,下一轮的输入为R1、R2、R3、R0,经过4次轮函数变换后寄存器的位置重新为R0、R1、R2、R3。因此,可以将SM4的4轮变换展开实现,迭代8次即可完成SM4加/解密操作。这样实现轮函数F既较少使用SIMD寄存器的个数,并且消除了不同SIMD寄存器内容之间的移动。轮函数F优化实现代码如下:
|
|
目前,SM4采用查表实现方法,实现思想简单,适用于多种平台。查表方法有2个明显的缺点:1)CPU在做查表操作时,由于SM4的表规模相对较大,表中的数据在内存和cache之间频繁对换导致查表延时较大;2)查表方法无法并行加/解密多组消息,这在一定程度上制约了SM4的软件实现性能。相比于查表方法,密码算法使用SIMD指令实现时,数据存放在SIMD寄存器中,读取数据延时较小,更重要的是SIMD指令在并行性方面有明显优势,如3.2.4节中轮函数F伪代码实现中使用的vpgatherdd指令可并行实现查表操作,vpxor(_mm256_xor_si256)指令可并行实现8组SM4消息32-bit字异或操作。此外,对于4-bit S盒及按块置换的线性层可使用vpshufb指令并行实现。表 2总结常见密码算法中的运算使用SIMD指令与否的区别。由表 2可知,相比于普通方法,SIMD指令实现具有明显的加速效果。
|
|
表 2 SIMD指令与普通实现对比 Table 2 SIMD implement compared with general implement cycles |
本节比较总结查表方法和SIMD技术并行实现SM4的性能,并比较SM4与AES的软件实现性能差异。评估SM4的软件实现性能是在3个不同处理器平台上进行,如表 3所示。
|
|
表 3 测试环境参数 Table 3 Test environment parameters |
表 4总结3个不同处理器上SM4采用查表和SIMD技术及AES采用查表方法和AES-NI指令的软件实现性能。评估分组密码算法软件实现性能的指标是算法每秒钟加/解密的比特数,即bps。表 4中的8-32(16-32)表示该方法采用8-bit(16-bit)输入32-bit输出表,SIMD技术1表示SM4四组消息并行实现方法,SIMD技术2表示SM4八组消息并行实现方法。
|
|
表 4 SM4/AES在不同处理器上的实验结果 Table 4 SM4/AES experimental results on different processors |
从表 4可以发现,SM4实现中采用8-bit输入32-bit输出表的软件实现性能均优于采用16-bit输入32-bit输出表,SM4采用SIMD技术2优于采用SIMD技术1。和目前SM4基于查表的软件实现性能相比,采用SIMD技术2(8-32),在Intel Core i3-4160平台Intel Core i7-5500U平台和Intel Core i7-6700平台上分别提高84.70%、97.69%和1.38倍。因此,SM4采用SIMD技术的软件实现性能有明显优势。此外,由表 4可知,SM4、AES在采用查表方法实现时,AES的查表软件实现性能稍具优势。SM4采用SIMD技术实现时,相比于AES查表实现有明显优势,但与AES-NI指令实现AES的软件实现性能相比仍有明显不足。
5 总结本文探讨国密SM4算法的软件优化实现方法。使用vpgatherdd指令解决了8-bit S盒不能使用SIMD指令并行实现的问题。利用SIMD技术,给出SM4轮函数中T变换的2种软件优化实现策略。实验结果表明,采用SIMD技术并行实现SM4,和目前基于查表的软件实现相比具有明显优势。相比于查表方法,采用SIMD技术,在Intel Core i3-4160处理器Intel Core i7-5500U处理器和Intel Core i7-6700处理器上的软件实现性能分别提高84.70%、97.69%和1.38倍。最后,通过实验比较总结SM4与AES的软件实现性能差异:在使用查表方法实现时,AES的查表实现性能稍具优势;SM4采用SIMD技术实现时,相比于AES查表实现有明显优势,但与AES-NI指令实现AES的软件实现性能相比仍有明显不足。此外,XOP指令集也支持本文使用的AVX2指令,因此,本文描述的SIMD技术并行实现方法也适用于AMD处理器平台。
| [1] |
国家密码管理局. GM/T0002-2012. SM4分组密码算法[S]. 北京: 中国标准出版社, 2012.
|
| [2] |
国家密码管理局. 国家密码管理局公告第23号[EB/OL]. (2012-02-21)[2017-01-20]. http://www.oscca.gov.cn/News/201204/News_1227.htm.
|
| [3] |
U. S. Department of Commerce/National Institute of Standards and Technology. Data encryption standard(DES), federal information processing standards publication[S/OL]. Gaithersburg, MD(1999)[2017-01-20]. http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf.
|
| [4] |
Daemen J, Rijmen V.
The design of Rijndael:AES-the advanced encryption standard[M]. Springer Science & Business Media, 2013.
|
| [5] |
Gueron S. Intel advanced encryption standard (AES) new instructions set[R/OL]. Intel White Paper Rev3. 01. (2012)[2017-01-20]. https://software.intel.com/sites/default/files/article/165683/aes-wp-2012-09-22-v01.pdf.
|
| [6] |
Intel: advanced vector extensions programming reference[R/OL]. Intel corporation (2009)[2016-12-29]. https://software.intel.com/sites/default/files/managed/39/c5/325462-sdm-vol-1-2abcd-3abcd.pdf.
|
| [7] |
Seiichi M, Shiho M. Lightweight cryptography for the cloud: exploit the power of bitslice implementation[C]//Prouff E, Patrick S. CHES 2012. Berlin Heidelberg: Springer, 2012: 408-425.
http://dl.acm.org/citation.cfm?id=2413347 |
| [8] |
Biham E. A fast new DES implementation in software[C]//Biham E. FSE1997. Berlin Heidelberg: Springer, 1997: 260-272.
http://link.springer.com/10.1007/BFb0052352 |
| [9] |
Bogdanov A, Knudsen L R, Leander G, et al. PRESENT: an ultra-lightweight block cipher[C]//Paillier P, Verbauwhede I. CHES 2007. Berlin Heidelberg: Springer, 2007: 450-466.
http://dl.acm.org/citation.cfm?id=1422007 |
| [10] |
Shibutani K, Isobe T, Hiwatari H, et al. Piccolo: an ultra-lightweight block cipher[C]//Preneel B, Takagi T. CHES 2011. Berlin Heidelberg: Springer, 2011: 342-357.
|
| [11] |
Neves S, Aumasson J P. Implementing BLAKE with AVX, AVX2, and XOP[J]. IACR Cryptology ePrint Archive, 2012, 2012:275.
|
| [12] |
Aumasson J, Henzen L, Meier W, et al. SHA-3 proposal BLAKE[J/OL]. Submission to NIST, 2008. [2017-01-20]. http://www.131002.net/blake/.
|
| [13] |
Ryad B, Guo J, Victor L, et al. Implementing lightweight block ciphers on x86 architectures[C]//Lange T, Lauter K. SAC 2013. Berlin Heidelberg: Springer, 2014: 324-351.
http://rd.springer.com/chapter/10.1007/978-3-662-43414-7_17 |
 2018, Vol. 35
2018, Vol. 35 


