2. State Key Laboratory of Low-dimensional Quantum Physics, and Collaborative Innovation Center of Quantum Matter, Department of Physics, Tsinghua University, Beijing 100084, China;
3. Department of Physics, Capital Normal University, Beijing 100037, China
2. 清华大学物理系低维量子物理国家重点实验室, 量子物质科学协同创新中心, 北京 100084;
3. 首都师范大学物理系, 北京 100037
Sympathetic cooling provides an efficient cooling of particles that are difficult to cool, especially for those particles which do not have optically accessible transitions[1-3]. Sympathetic cooling has achieved great success in many fields. In neutral-neutral sympathetic cooling, sympathetic cooling of an atomic Fermi gas by a Bose gas is a standard technology to study degenerate atomic Fermi gases and Boson-Fermion mixtures in many laboratories[4-6]. In ion-ion sympathetic cooling, usually one of the ionic species is directly laser cooled first and then cools the other ionic species by elastic collisions. Due to the strong Coulomb interaction V∝1/r, this is a highly effective method for cooling ions to cold and ultracold temperatures[7-9]. Recently, ion-ion sympathetic cooling was used to cool the molecular ion external degrees of freedom to ultracold temperature[10-11]. However, the long range ion-ion interaction does not couple to the molecular ion internal degrees of freedom and therefore the rovibrational temperature is unmodified by the ion-ion sympathetic cooling. Precise control over the internal motion of the molecular ions is required and useful in the study of ultrahigh-precision molecular spectroscopy[12], quantum control reactions[13], and ultracold chemistry[14-15].
Since the ion-neutral hybrid trap was originally proposed[3], which consists of two separate but spatially concentric traps (a magneto-optical trap (MOT) for the neutral species and a mass-selective linear Paul trap (LPT) for the ionic species), it becomes an ideal apparatus for ion-neutral sympathetic cooling[16-20]. In ion-neutral sympathetic cooling, collisions are dominated by the long range polarization potential, which can be described by -C4/r4, where C4=αe2/(8πε0), with α the static electric polarizability of the neutral spices and r the ion-neutral separation. Such long-range polarization forces between ions and neutral atoms result in large elastic scattering cross sections, as well as inelastic collision sections. Therefore, the ion-neutral sympathetic cooling offers a unique advantage to simultaneously cool both the internal and external degrees of freedom for molecular ions[21].
Before the invention of MOT, the ion-neutral sympathetic cooling was widely studied in the neutral buffer gas[22-24], in which the neutral buffer gas is usually dispersed throughout the whole experimental chamber. In those cases, the technique works best for ions (with mass mi) and neutral atoms (with mass mn) whose masses meet the criterion mi/mn>1, or else the ion trap's inherent atom-ion rf heating mechanism overwhelms the collisional cooling[22-24]. Unlike the buffer gas cooling, the cold neutral species is directly laser cooled and localized in a small volume compared to the volume of ions cloud in a LPT. Goodman et al.[19] have theoretically studied the ion-neutral sympathetic cooling in an ion-neutral hybrid trap, and shown that a MOT efficiently cools ions. Very recently, equal mass ion-neutral sympathetic cooling was observed experimentally within ion-neutral hybrid traps (See Refs.[17, 20]). They first reported evidence of sympathetic cooling of Rb+ by a Rb MOT and Na+ by a Na MOT, respectively.
In this paper, sympathetic cooling of Rb+ by cold Rb atoms is investigated in an ion-neutral hybrid trap. By directly mesruing the temperature of ions, the effect of LPT parameter q1, 2 on the sympathetic cooling of Rb+ is studied. Then an appropriate q1, 2 value is selected for further study of sympathetic cooling.
1 Experimental methodThe dynamic of a LPT will be introduced firstly to help us understanding the ion-atom collisions in the ion-neutral hybrid trap. The confining potential of a LPT is not conservative as it is based on oscillating electric fields, the trapped ions can be heated due to trap imperfections and rf heating caused by ion-ion repulsion[17, 19]. Even in a mixed systems of co-trapped ions and cold atoms, the collisions between ions and cold atoms can cause atom-ion rf heating mechanism[17-19]. The only available cooling channel for Rb+ ions in such an ion-neutral hybrid trap is collisions with cold Rb atoms. The heating and cooling of ions are simultaneous and competitive, therefore appropriate parameters of LPT must be selected to make sure that the collisional cooling can overwhelm many heating mechanisms[18-22].
The potential of the LPT is of the form
| $ \begin{array}{c} \Phi \left( {x, y, z, t} \right) \approx \frac{{{V_{{\rm{rf}}}}}}{{r_{_0}^{^2}}}{\rm{cos}}\left( {\mathit{\Omega} t} \right)({x^2}- {y^2}) + \\ \frac{{\eta {V_{{\rm{ec}}}}}}{{z_{_0}^{^2}}}[{z^2}-\frac{1}{2}({x^2} + {y^2})], \end{array} $ | (1) |
where Vrf and Ω is amplitude and frequency of the rf voltage respectively, Vec the electrostatic voltage on the end-cap, r0 the radial distance of the rf electrode from the centre of the LPT, and η the efficiency factor depends on the geometry of the end-cap electrode. The equation of motion for a single ion in the LPT can be described by the well-known Mathieu equation.
For a single ion with charge e and mass mi, the ranges of the so-called stability parameters ai and qi in which the ion can be trapped in the LPT are a1 < 0 and 0 < q1 < 0.9[8, 22]. The parameters ai and qi are defined as
| $ \begin{array}{l} {a_1} = {a_2} =-\frac{{{a_3}}}{2} = \frac{{-4e\eta {V_{{\rm{ec}}}}}}{{{m_{\rm{i}}}z_{_0}^{^2}{\mathit{\Omega} ^2}}}, \\ {q_1} =-{q_2} = \frac{{4e{V_{{\rm{rf}}}}}}{{{m_{\rm{f}}}r_{_0}^{^2}{\mathit{\Omega} ^2}}}, ({q_3} = 0), \end{array} $ | (2) |
And the total time-averaged kinetic energy 〈Ek〉 of the ion is defined as
| $ \left\langle {{E_k}} \right\rangle = \frac{1}{2}{m_{\rm{i}}}\left\langle {v_{_i}^{^2}} \right\rangle = \frac{{{m_{\rm{i}}}x_{_{0i}}^{^2}}}{4}(\omega _{_i}^{^2} + \frac{{q_{_i}^{^2}{\mathit{\Omega} ^2}}}{8}), $ | (3) |
where
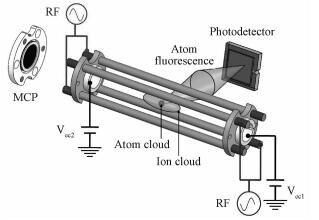
Our ion-neutral hybrid trap and processes of sympathetic cooling will be described as following. The detail description of our ion-neutral hybrid apparatus can be found in our previous work[25]. Here we will briefly describe the apparatus and experiments processes for the convenience of the reader. Figure 1 shows the schematic of our ion-neutral hybrid trap. The typical MOT is used to cool and trap cold 87Rb atoms with a maximum atom density up to na~1×1010 cm-3, with atom temperature 100~1 000 μK. Note that, the total number and the temperature of the cold atoms are directly measured by the time-of-flight (TOF) method[26]. The 87Rb+ ions are generated by two-step photoionization of cold 87Rb atoms and then trapped by a LPT, which is comprised of four radio frequency (rf) central parallel rods arranged in a quadrupole configuration and two dc hollow end-cap ring electrodes along the cylindrical axis. The microchannel plate (MCP) is used to detect the trapped ions by appropriately switching off the voltage on the hollow end-cap electrode closer to the MCP. The maximum number of ions is calculated by an equation
|
Download:
|
|
Fig. 1 Schematic of the ion-neutral hybrid trap in this work |
|
Both the cold atom cloud and ion cloud are located at center represented by the red sphere and blue cigar shape, respectively. The MCP is used to detect the ions. The MOT fluorescence is detected by a homemade photodetector.
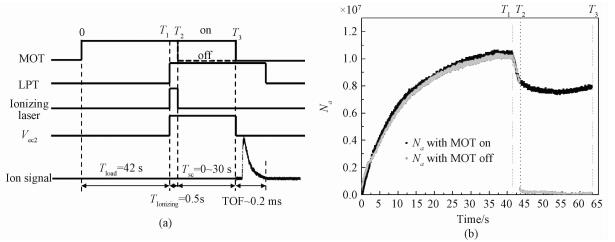
The sympathetic cooling of Rb+ ions is studied by measuring the changes of ion number Ni and temperature Ti after interaction with cold Rb atoms. Figure 2(a) shows the temporal sequence for one experimental cycle. In the first step, from 0 to T1, the MOT is turned on and loaded for as long as 42 s until saturation. In the second step, a blue diode continuous-wave laser at 473 nm is introduced to photoionize a small fraction of the cold atoms, and the LPT is turned on simultaneously to trap the ions. The duration of the ionizing laser is 500 ms from T1 to T2, with the laser intensity IPI=6.2 mW/cm2. Then, the LPT is kept on and the MOT is kept on for a durati on Tsc from T2 to T3 (MOT on) or turned off at T2 (MOT off), i.e., the ions collide with the MOT atoms in the hybrid trap or freely evolve in the LPT. At last the ions are released by switching off the electrostatic voltage Vec2 on the end-cap electrode close to the MCP rapidly at T3 (the MOT is turned off simultaneously if it works during Tsc). The rf voltage and electrostatic voltage on the other end-cap electrode Vec1 lag a little while (~5 ms) for the fully export of the ions. Figure 2(b) is a typical loading curve of the cold atoms with MOT on (dark line) and MOT off (grey line) from T2 to T3.
|
Download:
|
|
Fig. 2 Temporal sequence for one experimental cycle (a) and corresponding cold atom number in one experimental cycle (b) |
|
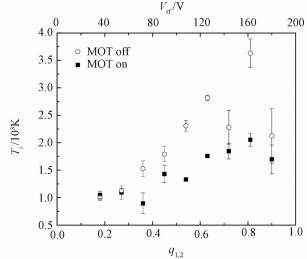
Goodman et al.[19] have theoretically studied the ion-neutral sympathetic cooling in an ion-neutral hybrid trap, and shown that sympathetic cooling effect is related to the ion-atom mass ratio and the parameters q1, 2 of the LPT. Here, we experimentally studied the effect of q1, 2 on the sympathetic cooling of Rb+ by cold Rb atoms in our ion-neutral hybrid trap. We fixed Ω=470 kHz and Vec1=Vec2=60 V, and changed |q1, 2| in the range of 0.18 to 0.90 by changing the Vrf based on equation (2), and the effect of q1, 2 on sympathetic cooling is studied by measuring the changes of Ti with MOT on and MOT off. Figure 3 shows that with MOT off a relationship of Ti∝q1, 22 which is expected by the equation (3). Such relationship is broken with MOT on and shows Ti with MOT on is lower than MOT off when 0.3≤|q1, 2|≤0.8. For further study, |q1, 2|=0.32 is selected with an lower initial Ti by setting the experimental parameters of the LPT as Ω=470 kHz, Vrf=70 V and Vec1=Vec2=60 V.
|
Download:
|
|
Fig. 3 Ion temperatures at different |q1, 2| values in the presence and absence of an overlapping MOT |
|
The solid squares are obtained with sympathetic cooling time of 20 s, and the hollow circles are obtained by only hold LPT 20 s. The LPT parameters are as following: Ω=470 kHz, Vec1=Vec2=60 V.
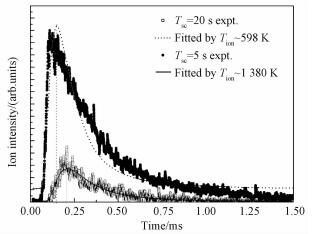
Figure 4 shows two typical TOF of ion signals with different sympathetic cooling time Tsc=5.20 s, respectively. Ti is estimated by fitting the TOF signal with a Maxwell-Boltzmann distribution as Ti≈(1 380±135) K and (598±55) K, correspondingly. Figure 4 also shows that the TOF signal follows a more well Maxwell-Boltzmann distribution with longer sympathetic cooling time Tsc, and this behavior indicates that the combined ion-atom system is intrinsically stable with longer sympathetic cooling time Tsc.
|
Download:
|
|
Fig. 4 Measured TOF profiles of ions with different sympathetic cooling time of 5 s and 20 s, and the corresponding fitting results by the Maxwell-Boltzmann distribution |
|
Figure 5 shows the number of ions Ni with different hold time of LPT with MOT off and MOT on, and the Ni decay curves shows the difference in trap loss with MOT on and MOT off. The lifetime of ions in LPT is extended via sympathetic cooling from 7 s to 15 s. Note that, the TOF ion signal becomes very weak after LPT hold 15 s with MOT off, we can not get exact the value of Ni and Ti. The error bar of Ni becomes smaller after LPT hold 15 s with MOT on and also indicates that the combined ion-atom system becomes more stable. This is very important for future cold chemistry experiments.

|
Download:
|
|
Fig. 5 Number of ions Ni vs.the hold time of LPT with MOT off and MOT on |
|
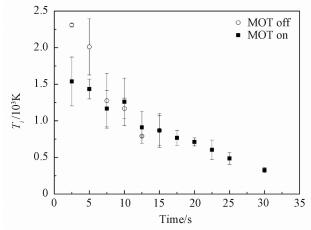
Figure 6 shows the temperature of ions Ti with different hold time in the LPT with MOT off and MOT on. The experimental results with MOT off show that Ti decreases with hold time of LPT in the first 12.5 s, and then does not decrease until the ion signal is too weak to be measured. In the case of MOT on, Ti decreases with hold time of LPT after the first 12.5 s which confirmed that ions are sympathetically cooled by cold atoms. More interestingly, Ti can be obtained as lower as Ti=(325±35) K with a relatively large number N≈1 500.
|
Download:
|
|
Fig. 6 Temperature of ions Ti vs. the hold time of LPT with MOT off and MOT on |
|
In summary, we studied the effect of LPT parameter q1, 2 on the sympathetic cooling of Rb+ ions by cold Rb atoms in an ion-neutral hybrid trap. By directly measuring the changes in ion number Ni and temperature Ti after interaction with cold atoms, we found obvious sympathetic cooling behavior with 0.3≤|q1, 2|≤0.8. At the |q1, 2| value of 0.32, sympathetic cooling was further investigated by two methods. The temperature of ions was cooled from the initial (2010±380)K to (325±35)K and the lifetime of ions in LPT was extended from 7 s to 15 s via sympathetic cooling. These findings are very useful for sympathetic cooling of atomic and molecular ions, especially for the ions without available optical channels.
| [1] |
Raizen M G, Gilligan J M, Bergquist J C, et al. Ionic crystals in a linear Paul trap[J]. Phys Rev A, 1992, 45(9):6493–6501.
DOI:10.1103/PhysRevA.45.6493 |
| [2] |
Birkl G, Kassner S, Walther H. Multiple-shell structures of laser-cooled 24Mg+ ions in a quadrupole storage ring[J]. Nature (London), 1992, 357:310–313.
DOI:10.1038/357310a0 |
| [3] |
Smith W W, Makarov O P, Lin J. Cold ion-neutral collisions in a hybrid trap[J]. J Mod Opt, 2005, 52(16):2253–2260.
DOI:10.1080/09500340500275850 |
| [4] |
Geist W, You L, Kennedy T A B. Sympathetic cooling of an atomic Bose-Fermi gas mixture[J]. Phys Rev A, 1999, 59(2):1500–1508.
DOI:10.1103/PhysRevA.59.1500 |
| [5] |
Schreck F, Ferrari G, Corwin K, et al. Sympathetic cooling of bosonic and fermionic lithium gases towards quantum degeneracy[J]. Phys Rev A, 2001, 64(1):011402.
DOI:10.1103/PhysRevA.64.011402 |
| [6] |
Brown-Hayes M, Wei Q, Presilla C, et al. Discrepancies in the resonance-fluorescence spectrum calculated with two methods[J]. Phys Rev A, 2008, 78(1):013617.
DOI:10.1103/PhysRevA.78.013617 |
| [7] |
Larson D J, Bergquist J C, Bollinger J J, et al. Sympathetic cooling of trapped ions:a laser-cooled two-species nonneutral ion plasma[J]. Phys Rev Lett, 1986, 57(1):70–73.
DOI:10.1103/PhysRevLett.57.70 |
| [8] |
Harmon T J, Moazzan-Ahmadi N, Thompson R I. Perpendicular dissociation of D2+ in intense Ti:sapphire laser pulses[J]. Phys Rev A, 2003, 67(1):013415.
DOI:10.1103/PhysRevA.67.013415 |
| [9] |
Zhang C B, Offenberg D, Roth B, et al. Comparative study of elastic electron collisions on the isoelectronic SiN2, SiCO, and CSiO radicals[J]. Phys Rev A, 2007, 76(1):012719.
DOI:10.1103/PhysRevA.76.012719 |
| [10] |
Schneider T, Roth B, Duncker H, et al. All-optical preparation of molecular ions in the rovibrational ground state[J]. Nat Phys, 2010, 6:275–278.
DOI:10.1038/nphys1605 |
| [11] |
Tong X, Winney A H, S Willitsch. Sympathetic cooling of molecular ions in selected rotational and vibrational states produced by threshold photoionization[J]. Phys Rev Lett, 2010, 105(14):143001.
DOI:10.1103/PhysRevLett.105.143001 |
| [12] |
Schiller S, Korobov V. Tests of time independence of the electron and nuclear masses with ultracold molecules[J]. Phys Rev A, 2005, 71(3):032505.
DOI:10.1103/PhysRevA.71.032505 |
| [13] |
Lamb H D L, McCann J F, McLaughlin B M, et al. Structure and interactions of ultracold Yb ions and Rb atoms[J]. Phys Rev A, 2012, 86(2):022716.
DOI:10.1103/PhysRevA.86.022716 |
| [14] |
Willitsch S, Bell M T. Chemical applications of laser-and sympathetically-cooled ions in ion traps[J]. Phys Chem Chem Phys, 2008, 10:7200–7210.
DOI:10.1039/b813408c |
| [15] |
Tacconi M, Gianturco F A, Belyaev A K. Computing charge-exchange cross sections for Ca+ collisions with Rb at low and ultralow energies[J]. Phys Chem Chem Phys, 2011, 13:19156–19164.
DOI:10.1039/c1cp20916g |
| [16] |
Schmid S, Harter A, Denschlag J H. Dynamics of a cold trapped ion in a Bose-Einstein condensate[J]. Phys Rev Lett, 2010, 105(13):133202.
DOI:10.1103/PhysRevLett.105.133202 |
| [17] |
Ravi K, Lee S, Sharma A, et al. Cooling and stabilization by collisions in a mixed ion-atom system[J]. Nat Commun, 2012, 3:1126.
DOI:10.1038/ncomms2131 |
| [18] |
Lee S, Ravi K, S .A. Rangwala. Measurement of collisions between rubidium atoms and optically dark rubidium ions in trapped mixtures[J]. Phys Rev A, 2013, 87(5):052701.
DOI:10.1103/PhysRevA.87.052701 |
| [19] |
Goodman D S, Sivarajah I, Wells J E, et al. Ion-neutral-atom sympathetic cooling in a hybrid linear rf Paul and magneto-optical trap[J]. Phys Rev A, 2012, 86(3):033408.
DOI:10.1103/PhysRevA.86.033408 |
| [20] |
Sivarajah I, Goodman D S, Wells J E, et al. Evidence of sympathetic cooling of Na+ ions by a Na magneto-optical trap in a hybrid trap[J]. Phys Rev A, 2012, 86(6):063419.
DOI:10.1103/PhysRevA.86.063419 |
| [21] |
Hudson E R. Method for producing ultracold molecular ions[J]. Phys Rev A, 2009, 79(3):032716.
DOI:10.1103/PhysRevA.79.032716 |
| [22] |
Major F G, Dehmelt H G. Exchange-collision technique for the rf Spectroscopy of Stored Ions[J]. Phys Rev, 1968, 170(1):91.
DOI:10.1103/PhysRev.170.91 |
| [23] |
Flatt B, Green M, Wodin J, et al. A linear RFQ ion trap for the enriched xenon observatory[J]. Nucl Instrum Methods Phys Res Sect A:Accelerators, Spectrometers, Detectors and Associated Equipment, 2007, 578(2):399–408.
DOI:10.1016/j.nima.2007.05.123 |
| [24] |
DeVoe R G. Power-law distributions for a trapped ion interacting with a classical buffer gas[J]. Phys Rev Lett, 2009, 102(6):063001.
DOI:10.1103/PhysRevLett.102.063001 |
| [25] |
Lv S F, Jia F D, Liu J Y, et al. Measurement of the low-energy Rb+-Rb total collision rate in an ion-neutral hybrid trap[J]. Chin Phys Lett, 2017, 34(1):013401.
DOI:10.1088/0256-307X/34/1/013401 |
| [26] |
Paul W. Electromagnetic traps for charged and neutral particles[J]. Rev Mod Phys, 1990, 62(3):531.
DOI:10.1103/RevModPhys.62.531 |
| [27] |
Meir Z, Sikorsky T, Ben-shlomi R, et al. Dynamics of a ground-state cooled ion colliding with ultracold atoms[J]. Phys Rev Lett, 2016, 117(24):243401.
DOI:10.1103/PhysRevLett.117.243401 |
 2018, Vol. 35
2018, Vol. 35 


