随着智能手机、平板电脑、可穿戴设备的普及,移动数据流量迅猛增长。为了满足用户对数据流量的需求,第五代移动通信系统应运而生。超密集网络①(ultra-dense network, UDN)作为5G的关键技术,通过部署更加密集的基站,能够提升频谱复用效率,实现百倍量级的系统容量提升[1-2]。超密集网络的部署将导致用户可能处于多个基站覆盖范围内,而传统的用户归属方案使得用户仅能归属到一个基站,其他基站将成为强干扰源,严重制约用户性能。一种有效的方案是采用多连接的用户归属方式[3],即一个用户可归属到多个基站,不同基站通过协作提升用户信号质量。值得注意的是,多连接场景下小区间干扰仍是限制系统性能的主要瓶颈,如何有效抑制小区间干扰需要进一步研究。基于上述背景,本文将研究多连接超密集网络中用户归属与干扰协调策略。
① 超密集网络,学术界有两种定义:用户密度大于基站密度[12-13];基站密度大于103 cells/km2[14]。
传统网络中的用户归属与干扰协调策略已得到广泛研究。文献[4-5]通过优化几乎空白子帧比例实现时域干扰协调,并基于边际效用优化用户归属,提出一种联合用户归属与干扰协调算法。文献[6-7]则在频域上实现干扰协调。文献[6]将总带宽划分为仅被微基站利用的频谱与可被所有基站利用的频谱两部分,并通过优化频谱分配比例与用户归属,提出一种频域干扰协调和用户归属联合优化方法。文献[7]则利用随机几何工具,联合优化频率复用因子与用户归属。文献[8]在仅考虑用户归属实现负载均衡研究的基础上,进一步考虑优化基站功率,提升系统吞吐量。文献[9]在异构网中研究用户公平性问题,将最小信噪比作为优化目标,通过联合优化用户归属和功率控制,最大化最小信噪比。
采用时域或频域干扰协调方法将带来无线资源的大量浪费。因此,本文重点关注用户归属与功率控制联合优化方法。然而已有研究均仅考虑单连接场景[10-11],多连接超密集网络下的用户归属与干扰协调方案仍有待进一步研究。为弥补该空白,本文从用户归属和功率控制的角度出发,采用兼顾系统吞吐量与用户公平性的对数和速率[7]作为优化目标。建立研究用户归属和功率控制的联合优化问题。该问题是一个非凸联合优化问题,难以直接求解。我们把原问题分解成用户归属和功率控制两个子问题,提出一种高效的求解算法。仿真结果显示,所提算法既保证了用户的公平性又能够提升系统吞吐量。
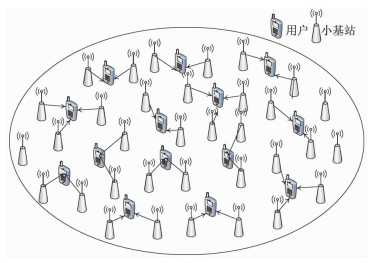
1 系统模型考虑由m个基站和n个用户组成的超密集网络,如图 1所示。基站和用户的集合分别为M={1, 2, …, m}和N={1, 2, …, n}。本文关注基站以极高密度部署的场景,该场景下的基站数量将大于用户数量,即m > n。
|
Download:
|
| 图 1 系统模型 Fig. 1 System model | |
在基站密集部署场景下,若考虑传统用户归属方式,将有大量基站处于空载状态。为解决该问题,本文假设多个基站可通过传输相同数据服务该用户,以提升信号质量。用变量xij表示基站i与用户j间的关系:
| $ {\rm{SI}}{{\rm{R}}_j} = \frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {\left( {1 - {x_{ij}}} \right){p_i}{g_{ij}}} }}. $ | (1) |
用W表示系统带宽,则用户j的速率可以表示为
| $ {R_j} = W{\log _2}\left( {1 + \frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {\left( {1 - {x_{ij}}} \right){p_i}{g_{ij}}} }}} \right). $ | (2) |
从式(2)可看出,不同的xij和pi会对用户速率产生影响,因此,设计高效的用户归属与功率控制策略以提升系统性能是十分必要的。
2 基于对数效用的用户归属以及功率控制 2.1 问题形成采用兼顾用户速率与用户公平性的对数和速率作为优化目标,用户归属与功率控制问题形成如下
| $ \begin{array}{l} {\rm{P1}}:\mathop {\max }\limits_{{p_i}, {x_{ij}}} \sum\limits_{j \in N} {{{\log }_2}} \left( {W{{\log }_2}\left( {1 + \frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {\left( {1 - {x_{ij}}} \right){p_i}{g_{ij}}} }}} \right)} \right)\\ {\rm{s}}{\rm{.t}}.\;\;{\rm{C}}1:{p_i} \le {p_{\max }}, \forall i \in M, \\ \;\;\;\;\;{\rm{C}}2:\sum\limits_j {{x_{ij}}} \le 1, \forall i \in M, \forall j \in N, \\ \;\;\;\;\;{\rm{C3}}:{x_{ij}} \in \left\{ {0, 1} \right\}, \forall i \in M, \forall j \in N. \end{array} $ |
约束1表示最大功率限制,约束2表示一个基站仅能服务一个用户,约束3为xij的取值范围。
优化问题P1为混合整数规划问题,难以求解。为有效求解该问题,本文提出一种启发式算法,将问题P1分解为用户归属和功率控制两个子问题,并分别对两个子问题进行求解,可以得出原问题的下界。
2.2 用户归属问题求解固定基站的发射功率,优化问题P1可转化为
| $ \begin{array}{l} {\rm{P2}}:\mathop {\max }\limits_{{x_{ij}}} \sum\limits_{j \in N} {{{\log }_2}} \left( {W{{\log }_2}\left( {1 + \frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {\left( {1 - {x_{ij}}} \right){p_i}{g_{ij}}} }}} \right)} \right)\\ {\rm{s}}{\rm{.t}}.\;\;{\rm{C}}2:\sum\limits_j {{x_{ij}}} \le 1, \forall i \in M, \forall j \in N, \\ \;\;\;\;\;\;{\rm{C3}}:{x_{ij}} \in \left\{ {0, 1} \right\}, \forall i \in M, \forall j \in N. \end{array} $ |
该问题仍为非凸问题,由于超密集网络基站间干扰严重,
| $ \begin{array}{l} {R_j} = W{\log _2}\left( {1 + \frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {\left( {1 - {x_{ij}}} \right){p_i}{g_{ij}}} }}} \right)\\ \;\;\;\; = - W{\log _2}\left( {1 - \frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {{p_i}{g_{ij}}} }}} \right)\\ \;\;\;\; \approx - W\left( {\frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {{p_i}{g_{ij}}} }} + 0.5{{\left( {\frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {{p_i}{g_{ij}}} }}} \right)}^2}} \right). \end{array} $ | (3) |
通过上述凸近似,并对约束3进行松弛可将问题P2转化为
| $ \begin{array}{l} {\rm{P3}}:\mathop {\max }\limits_{{x_{ij}}} \sum\limits_{j \in N} {{{\log }_2}} \left( {\frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {{p_i}{g_{ij}}} }} + 0.5{{\left( {\frac{{\sum\limits_{i \in M} {{p_i}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {{p_i}{g_{ij}}} }}} \right)}^2}} \right)\\ {\rm{s}}{\rm{.t}}.\;\;{\rm{C}}2:\sum\limits_j {{x_{ij}}} \le 1, \forall i \in M, \forall j \in N, \\ \;\;\;\;\;\;{\rm{C3}}:{x_{ij}} \in \left[{0, 1} \right], \forall i \in M, \forall j \in N. \end{array} $ |
问题P3是一个凸优化问题,可以通过标准凸优化算法求出其最优解。继而对xij进行离散化,重新转变为0或1,可以得到用户归属问题的次优解。
2.3 功率控制问题求解固定用户归属,优化问题P1可转化为
| $ \begin{array}{l} {\rm{P4}}:\mathop {\max }\limits_{{p_i}} \sum\limits_{j \in N} {{{\log }_2}} \left( {W{{\log }_2}\left( {1 + \frac{{\sum\limits_{i \in M} {p_i^{\left( k \right)}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M} {\left( {1 - {x_{ij}}} \right)p_i^{\left( k \right)}{g_{ij}}} }}} \right)} \right)\\ {\rm{s}}{\rm{.t}}.\;\;{\rm{C}}1:{p_i} \le {p_{\max }}, \forall i \in M. \end{array} $ |
问题P4是一个非凸问题,本文采用序贯凸规划[15]的方法获得局部最优解。
对目标函数进行一阶凸近似,近似结果为
| $ f\left( \mathit{\boldsymbol{p}} \right) \approx f\left( {{\mathit{\boldsymbol{p}}^{\left( k \right)}}} \right) + \nabla f{\left( {{\mathit{\boldsymbol{p}}^{\left( k \right)}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{p}} - {\mathit{\boldsymbol{p}}^{\left( k \right)}}} \right). $ | (4) |
其中:
| $ \nabla f\left( {p_i^{\left( k \right)}} \right) = \\ \sum\limits_{j = 1}^n {\frac{{\frac{{{g_{ij}}}}{{{{\log }_2}\left( {\sum\limits_{i = 1}^m {p_i^{\left( k \right)}{g_{ij}}} } \right)}} - \frac{{{g_{ij}}\left( {1 - {x_{ij}}} \right)}}{{{{\log }_2}\left( {\sum\limits_{i = 1}^m {p_i^{\left( k \right)}{g_{ij}}} \left( {1 - {x_{ij}}} \right)} \right)}}}}{{{{\log }_2}\left( {\sum\limits_{i = 1}^m {p_i^{\left( k \right)}{g_{ij}}} } \right) - {{\log }_2}\left( {\sum\limits_{i = 1}^m {p_i^{\left( k \right)}{g_{ij}}} \left( {1 - {x_{ij}}} \right)} \right)}}}, $ |
pi(k)(i=1, 2, …, m)为基站功率初值。
因此采用序贯凸规划方法得出的近似优化问题为
| $ \begin{array}{l} {\rm{P5}}:\mathop {\max }\limits_{{p_i}} f\left( {{\mathit{\boldsymbol{p}}^{\left( k \right)}}} \right) + \nabla f{\left( {\mathit{\boldsymbol{p}}\left( k \right)} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{p}} - {\mathit{\boldsymbol{p}}^{\left( k \right)}}} \right)\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;{\rm{C}}1:\left| {{p_i} - p_i^{\left( k \right)}} \right| \le \Delta, \forall i \in M. \end{array} $ |
问题P5是个线性规划问题,易求出其最优解,多次迭代,求出令目标函数值最大的那组功率值即为功率分配问题次优解。
2.4 用户归属与功率控制联合优化通过上述对用户归属问题和功率控制问题的分别求解, 可以得出联合优化问题的求解交替优化算法如下:
算法1(用户归属与功率控制联合优化):
1) 对pi(0)(i=1, 2, …, m)分别设置(0, 1)内的随机值作为其初始值;
2) 由标准凸优化求解方法求解问题P3,得出用户归属问题的解xij(i=1, 2, …, m; j=1, 2, …, n);
3) 对每个xij转化为离散的值(0或1),得到xij*;
4) 将xij*(i=1, 2, …, m; j=1, 2, …, n)代入问题P5,多次迭代求出令目标函数值最大的那组功率控制结果为pi(k+1),(i=1, 2, …, m);
5) 把pi(k+1)(i=1, 2, …, m)作为初始值,重复步骤2)、3)、4),直至
| $ \begin{array}{l} \left| {\sum\limits_{j \in N}^{} {{{\log }_2}} \left( {W{{\log }_2}\left( {1 + \frac{{\sum\limits_{i \in M}^{} {p_i^{\left( k \right)}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M}^{} {\left( {1 - {x_{ij}}} \right)p_i^{\left( k \right)}{g_{ij}}} }}} \right)} \right)} \right. - \\ \left. {\sum\limits_{j \in N}^{} {{{\log }_2}} \left( {W{{\log }_2}\left( {1 + \frac{{\sum\limits_{i \in M}^{} {p_i^{\left( {k + 1} \right)}{g_{ij}}{x_{ij}}} }}{{\sum\limits_{i \in M}^{} {\left( {1 - {x_{ij}}} \right)p_i^{\left( {k + 1} \right)}{g_{ij}}} }}} \right)} \right)} \right| < \varepsilon, \end{array} $ |
其中ε为精度门限。
3 仿真结果与分析仿真中设m=40和n=20,基站与用户均匀分布在200 m×200 m的范围内。路径损耗为PL(dB)=27.3+3.91×10×lgr(m),假设小尺度衰落为瑞利衰落,系统带宽为5 MHz,小站的最大传输功率为30 dBm。
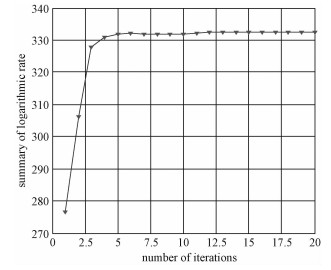
图 2为提出算法的对数和速率随算法迭代次数的变化情况。从图中可以明显看出所提迭代算法是收敛的,并且收敛速度较快,迭代5次之后,系统对数和速率即趋于稳定。
|
Download:
|
| 图 2 算法的收敛情况 Fig. 2 Astringence of the proposed algorithm | |
图 3为利用所提算法研究基站数目变化时,系统总吞吐量变化情况。可以看出系统总吞吐量随可用基站数的增加而增大。这是由于随基站总数增大,用户可利用的基站数量增加,所提算法约束范围变大,因此系统总吞吐量相应增加。

|
Download:
|
| 图 3 系统吞吐量随基站数变化曲线 Fig. 3 Total throughputs versus the number of BSs | |
为更好说明本文所提算法(proposed)性能,考虑以下对比算法:对比算法1为一种单连接用户归属方式(single association, SA),用户选择接入取得最大信干比的基站;对比算法2采用多连接的用户归属方式(multiple association, MA),用户接入距离门限以内的所有基站。
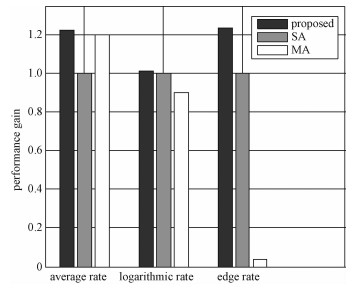
图 4比较不同算法的和速率、对数和速率及边缘用户速率。比较图 4中3种算法的平均速率,可以看出,所提多连接算法与对比算法2在平均用户速率上相比对比算法1分别有22.35%和19.91%的性能提升,说明采用多连接用户归属方式能够显著提升系统平均用户速率。这是因为多连接用户归属方式能够充分利用超密集网络中的基站,进一步提升用户速率。
|
Download:
|
| 图 4 所提算法与对比算法性能比较 Fig. 4 Performance comparison among the three algorithms | |
比较图 4中3种算法的平均对数速率,可以看出,所提算法与对比算法1在用户平均对数速率上明显优于对比算法2。这是因为对比算法2受周围基站数量影响较大,周围基站数目多的用户接入基站较多,用户速率很大; 而周围基站少的用户接入基站少,用户速率低。因此用户速率两极分化严重,导致平均对数速率较低。
比较图 4中3种算法的边缘用户速率,可以看出,边缘用户性能最好的是所提算法,其次是对比算法1,这两种算法均比对比算法2具有非常高的边缘用户性能提升。
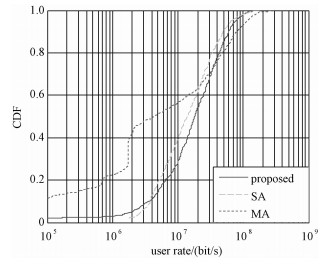
图 5给出提出算法与对比算法的CDF曲线,可以看出所提算法的CDF性能优于两对比算法的CDF性能。
|
Download:
|
| 图 5 所提算法与对比算法的CDF比较 Fig. 5 Comparison of CDF among the three algorithms | |
综上所述,所提算法在平均用户速率、平均对数和速率、边缘用户速率及CDF性能上均优于两对比算法。
4 结束语本文在超密集网络中,研究如何高效地利用密度更高的基站进一步提升系统性能。从用户归属和功率控制的角度出发,形成一个最大化系统对数和速率的优化问题。该问题难以求出其最优解,通过分别优化用户归属与功率控制,得出一种高效联合优化算法。最后通过系统级仿真,说明所提算法相较已有算法在兼顾用户公平性的同时能够明显提升系统吞吐量。
| [1] |
Shi Y, Zhang J, Letaief K B, et al. Large-scale convex optimization for ultra-dense Cloud-RAN[J]. IEEE Wireless[KG3*4] Communications, 2015, 22(3):84–91.
DOI:10.1109/MWC.2015.7143330 |
| [2] |
Hwang I, Song B, Soliman S S. A holistic view on hyper-dense heterogeneous and small cell networks[J]. IEEE Communications Magazine, 2013, 51(6):20–27.
DOI:10.1109/MCOM.2013.6525591 |
| [3] |
Kamel M I, Hamouda W, Youssef A M. Multiple association in ultra-dense networks[C]//Communications (ICC), 2016 IEEE International Conference on. IEEE, 2016: 1-6.
|
| [4] |
Jin Y, Qiu L. Joint user association and interference coordination in heterogeneous cellular networks[J]. IEEE Communications Letters, 2013, 17(12):2296–2299.
DOI:10.1109/LCOMM.2013.102113.131836 |
| [5] |
Jia Y, Zhao M, Zhou W. Joint User Association and eICIC for Max-Min Fairness in HetNets[J]. IEEE Communications Letters, 2016, 20(3):546–549.
DOI:10.1109/LCOMM.2016.2516002 |
| [6] |
Ikeda Y, Okasaka S, Hoshino M, et al. Proportional fair-based joint optimization of cell association and inter-cell interference coordination for heterogeneous networks[C]//2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall). IEEE, 2014: 1-5.
|
| [7] |
Lin Y, Yu W. Optimizing user association and frequency reuse for heterogeneous network under stochastic model[C]//2013 IEEE Global Communications Conference (GLOBECOM). IEEE, 2013: 2045-2050.
|
| [8] |
Chiang P H, Huang P H, Sun S S, et al. Joint power control and user association for traffic offloading in heterogeneous networks[C]//2014 IEEE Global Communications Conference. IEEE, 2014: 4424-4429.
|
| [9] |
Sun R, Hong M, Luo Z Q. Joint downlink base station association and power control for max-min fairness:Computation and complexity[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(6):1040–1054.
DOI:10.1109/JSAC.2015.2416982 |
| [10] |
徐茂, 张光荣, 陈晓辉, 等. 基于调和均值公平的多小区干扰协调功率分配算法[J]. 中国科学院大学学报, 2012, 29(5):659–666.
|
| [11] |
余林浩, 卢汉成, 洪佩琳. 一种带QoS约束的资源分配和ABS功率控制算法[J]. 中国科学院大学学报, 2015, 32(5):661–666.
|
| [12] |
Park J, Kim S L, Zander J. Asymptotic behavior of ultra-dense cellular networks and its economic impact[C]//2014 IEEE Global Communications Conference. IEEE, 2014: 4941-4946.
|
| [13] |
Stefanatos S, Alexiou A. Access point density and bandwidth partitioning in ultra dense wireless networks[J]. IEEE transactions on communications, 2014, 62(9):3376–3384.
DOI:10.1109/TCOMM.2014.2351820 |
| [14] |
Ding M, López-Pérez D, Mao G, et al. Will the area spectral efficiency monotonically grow as small cells go dense?[C]//2015 IEEE Global Communications Conference (GLOBECOM). IEEE, 2015: 1-7.
|
| [15] |
Hovgaard T G, Boyd S, Larsen L F S, et al. Nonconvex model predictive control for commercial refrigeration[J]. International Journal of Control, 2013, 86(8):1349–1366.
DOI:10.1080/00207179.2012.742207 |
 2018, Vol. 35
2018, Vol. 35 


