非连续变形分析(discontinuous deformation analysis, DDA)是由Shi[1]针对岩石非连续介质提出的一种新型力学数值分析方法,被视为“有限元(finite element method, FEM)的非连续版本”。与FEM类似,DDA也采用最小势能原理建立总体刚度矩阵,并通过求解平衡方程获得块体位移。但与FEM不同的是,DDA采用多时步计算,通过各时步小位移、小变形的累积,实现大位移与大变形;每一时步严格的接触检测,保证块体之间接触无侵入张开无拉力;DDA计算无需进行网格的划分与重构,以块体自身的形状作为“网格”,可为任意形状[2]。与离散元相比,DDA采用动力松弛,最小化系统势能隐式求解,块体接触无侵入,具有严格的收敛性与精确的计算结果[3];总体而言,DDA具备完全的运动学与数值可靠性、满足严格的平衡要求、遵守正确的能量守恒,是一种计算过程接近实际,严格遵守数学和力学原理的有效方法[4]。
目前,DDA已广泛应用于边坡稳定性分析、围岩变形与破坏、岩体水力耦合、节理岩体爆破、静力分析、计算机动画等多个方面[5-6]。在实际工程中,DDA面临的问题往往数据规模较大、结构形状复杂、物理参数不易确定,需要设定不同的参数进行多次计算,而每一次计算都需要大量的时间。提高DDA的计算效率有助于减少计算耗时,也允许分析人员使用更加真实的计算模型,获得更多的分析数据,提高结果的准确性。
本文关注的对象是DDA中方程组求解方法的选择。在每一次开闭迭代后都需要对方程组进行重新求解[7],解方程组耗时占据整个计算30%~70%的时间,如何选择一个高效的方程组求解算法对提升整体计算效率至关重要。
1 相关工作常用的线性方程组求解算法分为直解法与迭代法,前者包括高斯消元法、Cholesky分解法、孪生分解法、多波前法等,后者包括Jacobi迭代法、Gauss迭代法、松驰迭代法(successive over-relaxation method, SOR)、带预处理共轭梯度法(preconditioned conjugate gradient method, PCG)等[8]。在串行计算条件下,问题规模较小时DDA使用高斯消元法,问题规模较大时使用SOR。
在过去的数年中,提高DDA方程组求解效率的研究思路主要分为2种。一种是对方法本身进行修改或与其他类似方法耦合,将隐式求解的过程更改为显式求解,再采用并行方法进行加速[9]。显式求解无需合成总体刚度矩阵,数据相关性较低,适合GPU(graphic processing unit)的并行模式,往往可取得明显的加速效果,但是存在计算结果不够精确、不易稳定、可能不收敛的问题。另一种是专注于稀疏对称线性方程组的并行求解,可以选择不同的并行计算平台以及多种可并行实现的方程组求解算法。相关成果包括,在数值流形法中,CUDA并行块Jacobi迭代法求解方程组,获得了最高5倍的加速比[10];采用OpenMP并行块Jacobi迭代法求解DDA中的方程组,应用于地下洞室群的破坏模拟[7];采用CUDA并行PCG,针对DDA刚度矩阵天然分块,提出基于矩阵分割的GPU并行稀疏矩阵向量乘方法[11]。
2 算法并行实现 2.1 大型稀疏矩阵的存储DDA方程组求解的刚度矩阵A在使用稀疏存储图法进行缩减排序后以块压缩稀疏行(block compress sparse row, BCSR)的形式进行存储,每个单元为6×6的子矩阵,它们按矩阵行号从小到大依次排列,记录每行子矩阵在连续数组中的起始位置以及各子矩阵的列号,鉴于刚度矩阵A是对称矩阵,只存储了上三角及对角线子矩阵。在串行计算中,以上信息足以进行方程组求解,而在使用OpenMP或CUDA实现并行计算时,还需生成下三角部分矩阵行起始位置及列号。
2.2 并行性分析Jacobi迭代法是最基本的迭代法,算法复杂度低,数据相关性低,容易并行实现,但收敛速度相对较慢。对Jacobi迭代法的迭代输入进行即时更新就得到Gauss-Seidel迭代法,在此基础上引入松弛因子即为SOR。因为需要对迭代输入进行即时更新,SOR的数据相关性高,难以并行求解,但合适的松弛因子可大幅提高收敛速度。
PCG是Krylov子空间法在求解对称正定矩阵时的特殊情况,目前广泛应用于大型稀疏对称正定矩阵的并行求解,算法数据相关性低,收敛速度较高,但实现过程相对复杂,计算过程中有数次数据归约求和,这对并行计算是一个瓶颈。表 1对以上各算法的相关性质进行总结。
|
|
表 1 各算法性质 Table 1 Characters of different algorithms |
Jacobi迭代法的并行实现技术可视为共轭梯度法的一部分,以PCG为例说明并行实现流程。
2.3 OpenMP并行实现在使用OpenMP进行多核并行计算时,基于计算机核数创建线程数,每个线程以自启发的方式分配到目标块体,串行求解该块体的6个自由度。稀疏矩阵与向量乘中每个线程负责一行子矩阵与对应向量的点积。向量与向量乘中每个线程负责2个六维向量的点积,再调用OpenMP归约命令进行线程间求和。
OpenMP的并行模型为Fork-Join形式,Fork与Join之间的区域为并行区域。当初始线程遇到并行结构语句时,会创建一个线程组,并行执行接下来的指令,即Fork动作。在退出并行结构时,只有初始线程继续执行,其他线程结束,即Join动作。采用OpenMP并行实现Jacobi预处理共轭梯度法(JPCG),在向量运算的起始位置执行Fork动作开启并行区域,直到需要进行数据归约、标量运算或区域跳转时执行Join动作,结束当前并行区域,由此形成以下4个并行区域。
1) 并行区域一
① 计算稀疏矩阵向量乘积Ax0, 初始化i=1;
② 计算残差向量r0=b-Ax0;
③ 计算预处理因子M的逆,M由对角线子矩阵组成;
④ 计算方向向量p′0=r′0=M-1r0;
⑤ 计算r′0r0的值。
2) 并行区域二
① 计算稀疏矩阵向量乘积Ap′i-1;
② 计算p′i-1Ap′i-1的值;
③ 计算参数αi-1=r′i-1ri-1/p′i-1Ap′i-1。
3) 并行区域三
① 更新迭代结果xi=xi-1+αi-1p′i-1;
② 更新残差向量ri=ri-1-αi-1Ap′i-1;
③ 计算残差向量的模e=‖ri‖,判断e是否小于0.000 000 1, 是则结束,否则继续。
4) 并行区域四
① 计算r′i=M-1ri, r′iri;
② 计算βi-1=r′i-1ri-1/r′iri;
③ 更新方向向量p′i=r′i+βi-1p′i-1;
④ i=i+1,回到并行区域二。
2.4 CUDA并行实现在使用CUDA进行GPU并行计算时,每个线程将计算一个块体的一个自由度。稀疏矩阵向量乘中,一个CUDA Warp负责一行子矩阵与对应向量的点积,采用文献[11]中的方法对刚度矩阵进行分割,在不需要改变DDA原有的BCSR存储方式的前提下可对全局内存进行合并读取。向量与向量乘中一个线程负责2个元素的乘积,在CUDA block内部进行累加求和,传回全局内存后启用新的Kernel函数累加各CUDA block之间的数据。实现调用的Kernel包括:
a) kernelresetA:对刚度矩阵进行分割,以满足CUDA中并行矩阵与向量乘积的需要;
b) kernelinverse:对刚度矩阵A对角线上的6×6子矩阵求逆,即M-1;
c) kernelmulmatrix:计算刚度矩阵与各向量的乘积,包括:Ax0, Ap′i-1;
d) kerneladd:累加各CUDA Block的向量乘积计算结果,包括:r′i-1ri-1, p′i-1Ap′i-1, r′iri;
e) kernel1:计算r0=b-Ax0, p′0=r′0=M-1r0, r′i-1ri-1;
f) kernel2:计算p′i-1Ap′i-1;
g) kernel3:计算xi=xi-1+αi-1p′i-1, ri=ri-1-αi-1Ap′i-1, r′=M-1ri, r′iri;
h) kernel4:计算βi-1=r′i-1ri-1/r′iri, p′i=r′i+βi-1p′i-1。
3 效率影响因素目标矩阵的规模与条件数影响SOR迭代法、并行Jacobi迭代法及并行JPCG的计算效率。DDA刚度矩阵的规模由系统块体的约束条件决定,而矩阵条件数的大小受当前迭代步的时间步长与块体接触关系影响。
3.1 刚度矩阵规模非连续系统的块体个数决定总体刚度矩阵的维度。DDA通常采用一阶近似描述各块体的位移与变形。二维情况下,块体形心坐标为(x0 y0),该点的刚体位移为(u0 v0),块体绕形心点的转动角为r0,块体的法向与切向应变为(εx εy γxy),块体内任意一点的位移可由以上6个自由度表示:
| $ D = \left( {{u_0}\;\;{v_0}\;\;{r_0}\;\;{\varepsilon _x}\;\;{\varepsilon _y}\;\;{\gamma _{xy}}} \right), $ | (1) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {u, v} \right) = \\ \left( {\begin{array}{*{20}{c}} 1&0&{ - \left( {y - {y_0}} \right)}&{\left( {x - {x_0}} \right)}&0&{\left( {y - {y_0}} \right)/2}\\ 0&1&{\left( {x - {x_0}} \right)}&0&{\left( {y - {y_0}} \right)}&{\left( {x - {x_0}} \right)/2} \end{array}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \times D, \end{array} $ | (2) |
n个块体受力与运动方程组表示为
| $ \left( {\begin{array}{*{20}{c}} {{K_{11}}}& \cdots &{{K_{1n}}}\\ \vdots&\ddots&\vdots \\ {{K_{n1}}}& \cdots &{{K_{nn}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{D_1}}\\ \vdots \\ {{D_n}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} F\\ \vdots \\ {{F_n}} \end{array}} \right), $ | (3) |
矩阵K即为总体刚度矩阵,大小为6n×6n,其中每个Kij为6×6的子矩阵,Di与Fi为6×1的向量。
3.2 计算时间步长DDA采用多时间步计算,计算时间步长t代表当前步模拟的实际物理时间。t值越小,惯性作用对矩阵的影响越大,即刚度矩阵对角线元素的值越大,这样矩阵条件数越小,方程组更易收敛。计算时间步长可通过两种方式获得,即自动时间步长和固定时间步长,下面分别对其进行论述。
1) 自动时间步长
在自动时间步长情况下,DDA通过以下公式计算时间步长的大小,初始计算步,为以下方程组的正解:
| $ \begin{array}{l} \;\;\;\;\;{a_1}{t^2} + {a_2}t + {a_3} = 0, \\ t = \frac{{ - {a_2} + \sqrt {a_2^2 - 4{a_1}{a_3}} }}{{2{a_1}}}, \end{array} $ | (4) |
后续计算步中为以下方程的正解:
| $ \begin{array}{l} \;\;\;\;\;{a_1}{t^2} + 2{a_2}t + 2{a_3} = 0, \\ t = \frac{{ - {a_2} + \sqrt {a_2^2 - 2{a_1}{a_3}} }}{{{a_1}}}, \end{array} $ | (5) |
其中a1、a2分别为上一步计算中最大位移块体的加速度与速度,a3为一步计算中允许的最大位移量[12]的负值,结合一元二次函数的特性分析系统在各运动阶段t的取值:
① 初始运动阶段:系统内各块体相互约束,块体速度几乎为零,a1相对较大,忽略a2的影响t=k|a3/a1|1/2,在此阶段|a1|与t成反比,|a3|与t成正比,t的值往往较小。
② 运动加剧阶段:位移量最大的块体基本脱离接触约束,a2变大,t的值主要受a3影响,与|a3|成正比。
③ 运动稳定阶段:在一系列运动变化后系统状态趋于稳定,a2几乎为零,|a1|的值较小,t的值往往较大。
2) 固定时间步长
固定步长主要应用于系统添加地震波的模拟计算,在计算初始被人为设定。地震波的加速度按时间等间隔分布,采用固定时间步长易于在分析过程中设定地震波参数。一般情况下,固定时间步长的取值相对自动时间步长较大。
3.3 块体接触关系DDA在建立刚度矩阵时会考虑块体之间的接触力及摩擦力,这是唯一会对刚度矩阵非对角线非零子矩阵位置造成影响的因素。对非对角线子矩阵,仅当块体与块体发生接触时值不为0。块体接触关系直接影响到刚度矩阵非零元素的位置分布,从而影响到矩阵的性态。对一个性态良好的矩阵应满足正定、对称、非零元集中在对角线附近的特性。
块体接触关系复杂度由模型节理数量、走向及间距决定。对节理组数少,同一组节理走向一致,间距大小差异小的算例,刚度矩阵非零元分布更加规律,非零元位置集中,接触关系复杂度较低。相反,对节理组数多,节理走向不一致,节理间距大小差异大的算例,刚度矩阵非零元分布更加零散,接触关系复杂度高。
4 实验与分析比较对于不同的问题规模、计算时步长、块体接触关系,各方程组求解算法表现出的性能有所差异。本节的主要工作是记录SOR迭代法、并行Jacobi迭代法及并行JPCG在不同条件下的计算耗时,分析比较实验结果。测试的CPU算法包括:SOR迭代法(SOR)、OpenMP并行Jacobi迭代法(PJ)、OpenMP并行JPCG(PJPCG);GPU算法包括:CUDA并行Jacobi迭代法(CJ)、CUDA并行JPCG(CJPCG)。使用的CPU(central processing unit)为Intel core i5 2400,核数为4,主频为3.1 GHz;使用的GPU为TESLA C2070,一共14个流多处理器,448个CUDA核,每个核的频率为1.15 GHz。
4.1 问题规模对算法效率的影响测试该测试的目的是确定不同计算规模下最优的方程组求解算法。如图 1所示,测试算例1为一边坡,模型中有两组节理,通过调整两组节理各自的节理面间距获得不同块体数目的模型,块体数目从最小的95到最大的3 503,计算步数为3 000,计算时步长自动。

|
Download:
|
| 图 1 不同节理间距的边坡模型 Fig. 1 Models with different joint distances | |
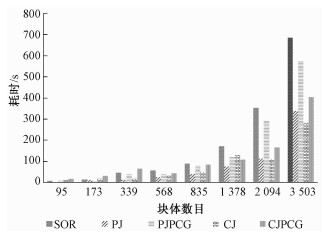
采用测试的方程组求解算法分别计算以上8个模型,图 2记录各算法的计算耗时。其中SOR迭代法的计算效率始终低于并行算法,并且随着块体数的增加差距越来越大。在1 378块之前OpenMP并行效率高于CUDA并行,GPU加速的优势在块体数目大于1 000后逐渐表现出来。当块体数目较少时,由于主机与设备之间数据传输的耗时以及无法利用所有的CUDA核,计算速度不如CPU并行。并行Jacobi迭代法效率高于并行JPCG,原因与该算例的接触关系密切相关,将在4.3节进一步分析。
|
Download:
|
| 图 2 不同问题规模下各求解算法耗时 Fig. 2 Equation solving time at different scales | |
1) 自动时间步长
该测试的目的是观察在自动步长下,随着系统状态变化,方程组求解算法效率的改变。如图 3所示,测试算例2与算例1相比,节理组数更多,走向更加复杂,共计4 361个块体,计算时步长自动,计算步数为20 000。

|
Download:
|
| 图 3 算例2 Fig. 3 Model of case 2 | |
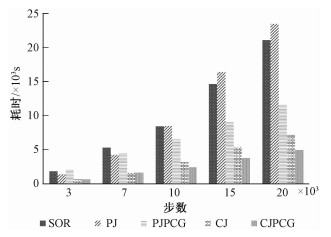
采用测试的方程组求解算法计算算例2,图 4记录在3 000、7 000、10 000、15 000及20 000步时各自的耗时情况。在3 000步之前,PJPCG效率低于PJ,CJPCG效率与CJ相当。此时系统处于初始运动状态,DDA自动获取的计算时步长小,这使得惯性力影响较大,刚度矩阵对角线绝对占优,方程组迭代求解容易收敛,并行Jacobi迭代法相对于SOR与并行JPCG,避免了收敛速度慢的缺点,而体现了算法简单的优点。在3 000步以后系统脱离初始运动状态,计算时步长增大,刚度矩阵性态变差,方程组开始难以收敛。并行Jacobi迭代法每一计算步的迭代次数增加,SOR与并行JPCG的收敛速度优势在此表现出来,在10 000步之后SOR迭代法效率也高于PJ。
|
Download:
|
| 图 4 算例2不同计算步下各求解算法耗时 Fig. 4 Equation solving time with different computation steps in case 2 | |
2) 固定时间步长
固定时间步长的取值范围一般为5~20 ms,在这个值下刚度矩阵的性态比较差,方程组求解十分缓慢,对于这种情况各算法的计算效率也会不同。测试模型与算例2相同,计算步数为10 000步。
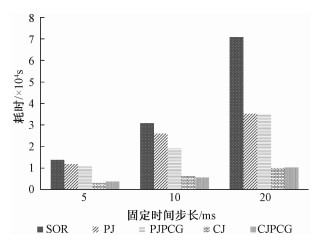
图 5记录固定时间步长分别为5、10、20 ms时,各求解算法的计算耗时。固定时间步长相对自动时间步长较大,方程组求解难度增加,并行的额外开销所占比例下降,带来的加速比增加,从而并行Jacobi迭代法与并行JPCG效率都高于SOR。并行Jacobi迭代法在此情况下难以收敛,故效率低于并行JPCG。
|
Download:
|
| 图 5 不同固定时间步长下各求解算法耗时 Fig. 5 Equation solving time with different fixed time steps | |
对于不同的算例甚至同一个算例在不同条件下的建模,块体之间的接触关系都是不同的, 这使得总体刚度矩阵的性态也有所差别。通过调整算例1两组节理间隙,获得块体数为4 778的算例3,计算步数为20 000步,时间步长自动,将测试结果与图 4中算例2的耗时做比较,分析块体接触关系对算法效率的影响。
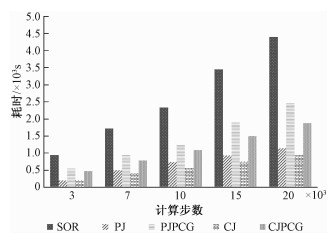
图 6记录算例3在3 000、7 000、10 000、15 000及20 000步时各算法的耗时情况。不管在CPU还是GPU端,并行Jacobi迭代法的效率都是最优的,其次为并行JPCG,这与算例2的实验结果有所不同。
|
Download:
|
| 图 6 算例3不同计算步下各求解器耗时 Fig. 6 Equation solving time with different computation steps in case 3 | |
比较算例2与算例3,二者块体数目近似,计算步数相同,都采用自动时间步长,但前者节理组数多,节理走向及间距都不一致,接触关系复杂度高,刚度矩阵的性态较差。后者只有两组节理,且节理组各自的走向与间距都一致,大部分块体都只与上下左右的相邻块体接触,接触关系复杂度低,刚度矩阵的性态较好。比较并行Jacobi迭代法与并行JPCG,前者难以收敛但算法简单,后者收敛性好但算法复杂。
在算例3中,天然性态较好的刚度矩阵掩盖了Jacobi迭代法难以收敛的缺点,而算法简单的优势在此体现。计算过程中,发生大位移的块体较少,仅仅为岸坡表面的少数块体,大量块体的位置与接触关系都没有变化,上一步的计算结果与下一步的很接近,而上一步的计算结果会作为下一步的计算初值,这也使得迭代更容易收敛。
此外,该算例中GPU加速效果并不明显,CJPCG依然次于PJ。对计算程序进一步测试后表明GPU上的任务分配不均,测试GPU负载,某个流多处理器的任务量2倍于平均任务量,这与刚度矩阵非零元的分布有关系。
5 经验公式 5.1 公式推导由实验结果可知,块体数量、计算时间步长、块体接触关系复杂度是影响计算效率的3个因素。块体数量n决定选择CPU或GPU,引入参数f1,当n < 1 000时f1=0选择CPU算法,否则f1=1。
计算时间步长与块体接触关系复杂度影响选择Jacobi迭代法或JPCG。当计算时间步长为自动、系统处于初始运动状态或块体接触复杂度低时选择Jacobi迭代法,否则选择JPCG。当为固定时间步长时,选择JPCG。引入参数f2,当系统处于初始运动状态时为0,否则为1;引入参数f3,当块体接触关系复杂度低时为0,否则为1;引入固定时间步长参数λ,自动时间步长时为0,否则为1。推导出选择Jacobi迭代法或JPCG的经验公式
| $ f = \left( {{f_2}\& {f_3}} \right)||\lambda 。$ | (6) |
当f=0时,选择Jacobi迭代法,当f=1时,选择JPCG。与参数f1相结合得到最终的经验公式表达式(7),
| $ f = {f_1} \times 2 + \left( {{f_2}\& {f_3}} \right)||\lambda 。$ | (7) |
当f=0时,选择PJ;当f=1时,选择PJPCG;当f=2时,选择CJ;当时f=3,选择CJPCG。
5.2 公式验证选择8组算例对以上公式进行验证,表 2为各算例的参数与验证结果。其中第3、4、5组数据的实际结果与公式结果不同,主要区别在于CPU或GPU的选用,在4.3节中提到该算例GPU加速欠佳,原因是各流多处理器上任务分配不均。基于该公式,DDA可在计算的每一步实时选择最优的方程组求解方法。
|
|
表 2 DDA方程组求解方法选择经验公式验证结果 Table 2 Verification of the empirical formula for choosing optimal equation solving methods |
本文基于多核或GPU平台,并行实现Jacobi迭代法与JPCG。分析并测试了问题规模、计算时间步长及块体接触关系对方程组求解效率的影响。基于测试结果总结出供DDA实时选择方程组求解算法的经验公式。研究表明随着计算规模的增大,GPU可以获得比CPU更优的计算效率;系统脱离初始运动状态、使用固定时间步长、块体接触关系复杂度高都会导致收敛难度增加,在收敛难度大的情况下,JPCG优于Jacobi迭代法。文中使用的CPU或GPU并行算法可继续优化,并行方面可以考虑使用MPI多机并行,在接下来的工作中将进一步完善提高。
| [1] |
Shi G H. Discontinuous deformation analysis:a new numerical model for the statics and dynamics of block systems[J]. Engineering Computations, 1992, 9(2):157–168.
DOI:10.1108/eb023855 |
| [2] |
石根华.
数值流形方法与非连续变形分析[M]. 北京: 清华大学出版社, 1997: 92-93.
|
| [3] |
Bobet A, Fakhimi A, Johnson S, et al. Numerical models in discontinuous media:review of advances for rock mechanics applications[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(11):1547–1561.
DOI:10.1061/(ASCE)GT.1943-5606.0000133 |
| [4] |
Zheng H, Jiang W. Discontinuous deformation analysis based on complementary theory[J]. Science in China Series E:Technological Sciences, 2009, 52(9):2547–2554.
DOI:10.1007/s11431-009-0256-4 |
| [5] |
Shi G H.
Applications of discontinuous deformation analysis (DDA) to rock engineering[M]. Computational Mechanics: Springer Berlin Heidelberg, 2007: 136-147.
|
| [6] |
刘婷婷, 王颖. 基于数值流形法的计算机动画建模[J]. 中国科学院研究生院学报, 2008, 25(6):843–848.
|
| [7] |
付晓东, 盛谦, 张勇慧. 基于OpenMP的非连续变形分析并行计算方法[J]. 岩土力学, 2014, 35(8):2401–2407.
|
| [8] |
Yousef S.
Iterative methods for sparse linear systems[M]. Philadelphia, Pennsylvania, United States: Society for Industrial and Applied Mathematics, 2003: 95-102.
|
| [9] |
Mikola R G, Sitar N. Explicit three dimensional discontinuous deformation analysis for blocky system[C]//47th US Rock Mechanics. Geomechanics Symposium. American Rock Mechanics Association, 2013.
|
| [10] |
Miao Q, Huang M, Wei Q. Parallel computing of numerical manifold method with openMP[C]//Information, Computing and Telecommunication. Yc-Ict'09. IEEE Youth Conference on. IEEE, 2009: 174-177.
|
| [11] |
Xiao Y, Miao Q, Huang M, et al. Parallel computing of discontinuous deformation analysis based on graphics processing unit[J]. International Journal of Geomechanics, 2016:E4016010.
|
| [12] |
Ning Y, Yang Z, Wei B, et al. Advances in two-dimensional discontinuous deformation analysis for rock-mass dynamics[J]. International Journal of Geomechanics, 2016:E6016001.
|
 2018, Vol. 35
2018, Vol. 35 


