2. University of Chinese Academy of Sciences, Beijing 100049, China
2. 中国科学院大学, 北京 100049
Land surface temperature (LST) has significant effects on resource formation, plant growth, climate environmental change, disaster monitoring, and animal and human activities, etc.[1]. Nowadays the acquisition means of land surface temperature map in large scale is mainly through thermal infrared remote sensing. However, as shown in Ref.[2] retrieving LST from thermal infrared remote sensing data is challenging because it presents an ill-posed problem that we obtain N spectral measurements of radiance but need to find N+1 unknowns (N emissivities and one temperature). Without prior information, we cannot accurately retrieve the land surface temperature and emissivity simultaneously. Meanwhile, land surface temperature retrieval is largely affected by atmosphere and emissivity. Actually, the error caused by the emissivity correction is two times that of atmosphere correction[3]. One percent error in emissivity can lead to an error on the LST up to 0.4 K[4]. In particular, in urban areas, the natural surfaces are covered by artificial materials with different thermal properties. Though, in a small area, it may be consisted of different materials and the emissivity varies obviously. Therefore, retrieving the land surface emissivity precisely is of utmost significance.
With the development of multi-spectral sensors such as advanced spaceborne thermal emission and reflection radiometer (ASTER), moderate resolution imaging spectroradiometer (MODIS), a mass of methodologies has been proposed and developed to retrieve surface emissivity and LST from multi-spectral data. In general, these methodologies can be largely divided into two categories: conventional approach and classification-based approachs[5-10]. The conventional approach solves the ill-posed problem through adding empirical formulas or some assumptions. A typical algorithm of the conventional approach is the temperature emissivity separation (TES)[11] which is the common algorithm for retrieving LST and emissivity from ASTER data. However, the accuracy of this algorithm depends on the empirical relationship between emissivity values with spectral contrast and atmospheric correction. Based on a great deal of experiments, the emissivity error of TES is within ±0.015[11]. The conventional approach has a complicated process and a relatively large deviation. The classification-based algorithms further categorize the land surface into several certain cover types and each type is characterized by a different emissivity value. The normalized difference vegetation index (NDVI) thresholds method considers that land cover is consisted of vegetation and soil. Whereas using the NDVI threshold method is not capable of retrieving emissivity precisely. Other methods increase the classification categories. Sobrino et al.[12] categorize the city of Madrid land surface into twelve different cover types based on the maximum likelihood rule, the error of retrieving bright temperature decreases by 3.5-4 ℃. However, the number of categories there should be there to precisely retrieve emissivity is uncertain and the methods based on classification use a constant emissivity value for several different land covers.
With the development of machine learning, a lot of problem is trying to solve based on machine learning. Neural network is widely used to obtain biophysical parameters[13]. Mao et al[14-15] retrieves land surface emissivity and land surface temperature based on neural network, and the average error of emissivity in MODIS band 31 is lower than 0.008. Wang[16] uses neural network to predict land surface and atmosphere parameters. However, these methods based on neural network use infraed bands, other model or atmosphere condition. They can not be applied to retrieve emissivity for single channel thermal infrared satellite.
Emissivity and reflectance are both inherent properties of substances. The proposed methods use reflectance data based on different classification techniques to categorize land surface into certain cover types and each type is characterized by a certain emissivity value. Hence, we can use multi-channel reflectance data to obtain emissivity map directly. Meanwhile, the non-linear relationship between reflectance data and emissivity can be solved using the back-propagation neural network (BPNN) effectively.
1 MODIS and materialMODIS is designed for the NASA's earth observing system (EOS) and mission to planet earth programs[17]. The EOS provides global observations and scientific data of land cover changes and global productivity, surface temperature and emissivity, atmosphere and climate changes, etc. MODIS is an imaging spectroradiometer carrying 490 detectors, arranged in 36 spectral bands that covers the visible and infrared spectrum (0.4-14.3 μm). The spatial resolutions for group 1 which is consisted of band 1 and band 2, group 2 with bands from band 3 to band 7 and group 3 with bands from band 8 to band 36 are 250, 500, and 1 000 m respectively. The reflected solar bands include bands from band 1 to band 19 and band 26 while the rest are emissive infrared bands.
The MODIS L1B data is relatively original data. The MODIS data products produced by the L1B data are diverse. MOD11 product includes land surface temperature data and land surface emissivity data.
Reflectance data (L1B) and its emissivity data (MOD11) are utilized to train the BPNN in this paper. Besides, the input of the BPNN is the reflectance data in bands from band 8 to band 13 and the output is emissivity data in band 31.
2 Methodology 2.1 NDVI thresholds methodThe NDVI thresholds method is simply classification based. The method assigns appropriate emissivity value to each pixel of an image based on the proportion of vegetation[18]. We can calculate the proportion of vegetation according to Eq. (1).
| $ {P_{\rm{v}}} = {\left( {\frac{{{\rm{NDVI}} - {\rm{NDV}}{{\rm{I}}_{\rm{s}}}}}{{{\rm{NDV}}{{\rm{I}}_{\rm{v}}} - {\rm{NDV}}{{\rm{I}}_{\rm{s}}}}}} \right)^2}. $ | (1) |
Where Pv is the proportion of vegetation, NDVI can be obtained from Eq.(2), NDVIs is the minimum NDVI value which is not less than 0, and NDVIv is the maximum NDVI value which is not greater than 1.
When NDVI value is lower than 0, we assign 0 to Pv and when NDVI value is greater than 1, assign 1 to the Pv.
| $ {\rm{NDVI}} = \frac{{\left( {{\rm{NI}}{{\rm{R}}_{{\rm{reflect}}}} - {\rm{Re}}{{\rm{d}}_{{\rm{reflect}}}}} \right)}}{{\left( {{\rm{NI}}{{\rm{R}}_{{\rm{reflect}}}} + {\rm{Re}}{{\rm{d}}_{{\rm{reflect}}}}} \right)}}. $ | (2) |
Where NIRreflect is the spectral reflectance in the near infrared region, Redreflect is the spectral reflectance in the red region.
Finally, assume that each pixel is composed of soil and vegetation. The soil emissivity and vegetation emissivity is set to 0.97 and 0.985[10], respectively. In addition, when Pv is equal to 1, the emissivity of the pixel is set to 0.99. The emissivity map can be obtained according to Eq. (3)
| $ \varepsilon = {\varepsilon _{\rm{v}}}{P_{\rm{v}}} + {\varepsilon _{\rm{s}}}\left( {1 - {P_{\rm{v}}}} \right) + 4 < d\varepsilon > {P_{\rm{v}}}\left( {1 - {P_{\rm{v}}}} \right), $ | (3) |
Where ε is the emissivity value, εv is the vegetation emissivity value, εs is the soil emissivity value, and < dε> is a coefficient and set to 0.015.
2.2 Back-propagation neural network methodBPNN method is used to retrieve emissivity pixel-by-pixel in this paper. The advantage of BPNN is that we can directly obtain emissivity map from satellite observation data[14] without categorizing land surface into certain cover types.
There are some unavailable pixels (MODIS L1B reflectance DN > 32 767) in each band. Meanwhile, with the increase of input bands to the BPNN, the number of unavailable pixels is increasing rapidly. The purpose of this paper is verifying the feasibility of proposed method. Therefore, we choose reflectance data in bands from band 8 to band 13 (visible port data) and its emissivity in band 31 from MODIS scene image as the input and the output of the BPNN respectively. We obtain 197 959 training samples from the MODIS scene image (MOD021KM.A2015275.0210.005. 2015278202333.HDF). Each training sample is a vector consisted of six reflectance values in bands from band 8 to band 13 and its emissivity value in band 31. We train the BPNN based on the training sets and test the trained BPNN through another MODIS scene image (MOD021KM.A2015275. 0350.005.2015278202816.HDF). The test scene image is different from the training scene image in geographical location and time.
We need to determine four key parameters of BPNN: the number of hidden layers, the node number of each hidden layer, the transfer function, and training termination condition. Taken into account the non-linear relationship between the input data and output data, the complexity of the model, the computational efficiency and empirical structure design, we set three hidden layers to solve the problem, and each hidden layer has log2N nodes, where N is the number of input layer samples. The transfer function is 'logsig' function. The training termination condition takes mean square error (MSE) as the decision rule, and the MSE is set to 3×10-6.
To solve the over-fitting problem, the gradient threshold andvalidation checks are set to 1×10-7 and 6 respectively. If the gradient decreases by less than 1×10-7 in one training epoch or the training accuracy has not improved for 6 training epochs, we stop training the BPNN.
Remote sensing image contains abundant information, including spectral features and texture features. Texture features are the representations of local structural information of remote sensing image. We make full use of the spectral and texture features to retrieve land surface emissivity map.
GLCM(gray level co-occurrence matrix) algorithm is one of the most widely used methods to extract texture features in remote sensing community[19-22]. GLCM shows the comprehensive information of the image. Due to the fact that the paper obtains emissivity map pixel-by-pixel through BPNN using visible channel reflectance data in MODIS, the gray value in the image is associated with the properties of the land surface. The relationship between a pixel and its neighboring pixels changes due to angular, distance and changed range and speed with different land surfaces. The second-order statistical analysis based on GLCM can achieve a better description of texture features. Hence, texture features are extracted based on GLCM in each patch (15×15) which is consisted of one pixel in the center and its neighboring pixels in bands from band 8 to band 13.
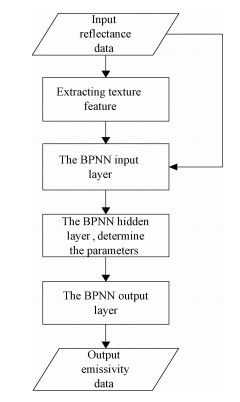
Firstly, use the reflectance data in bands from band 8 to band 13 to calculate 4 GLCMs in four directions: 0°, 45°, 90°, 135° respectively. Taken time consume and complexity into account, image gray levels are set to 8. For each patch in bands from band 8 to band 13, four different GLCMs are calculated. Then, the four parameters: contrast, correlation, energy, and homogeneity which are obtained from the gray level co-occurrence matrixes are final descriptors of texture features. Finally, each training sample contains 6 reflectance values (bands 8-13) and corresponding 96 (6×4×4) texture features. The training process is shown in Fig. 1.
|
Download:
|
|
Fig. 1 Flowchart of the BPNN method based on reflectance data and texture features |
|
In the process of training the BPNN, mean squared error (MSE) is the decisive criterion of finishing the training. The MSE threshold is set to 3×10-6. Then, we test the BPNN with different scene images. For the test image, we get emissivity map via NDVITM and BPNN methods. The following three methods are used to analyze the retrieval results.
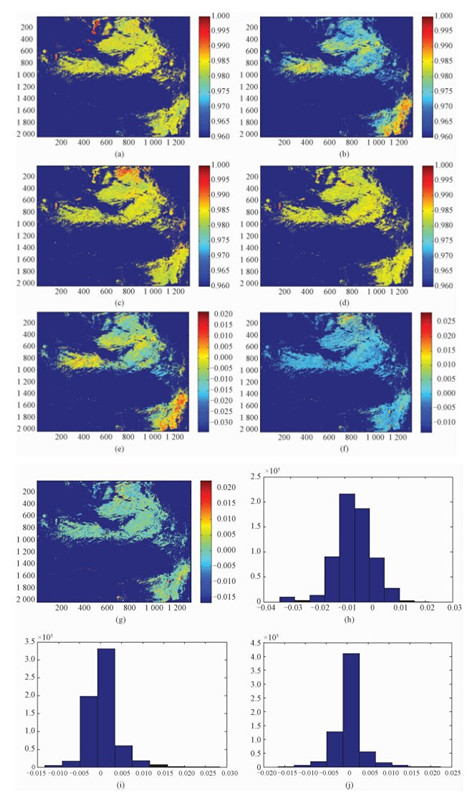
To test the performance of trained BPNN and analyze the influence of texture features, the input nodes of the BPNN are the reflectance data in bands from band 8 to band 13 with or without its texture features. The output of the BPNN is emissivity in band 31. We get the emissivity maps via NDVITM and BPNN method and then compare the retrieval results with MODIS emissivity product. Figure 2 shows the MODIS emissivity product, retrieval emissivity results, the error distribution and the error statistics based on NDVITM and BPNN respectively. In Fig. 2, 2(a) is MODIS emissivity product image, and 2(b) is emissivity image retrieved based on NDVITM, and 2(c) is emissivity image retrieved based on BPNN (input data are spectral features), and 2(d) is emissivity image retrieved based on BPNN (input data are spectral and texture features), and 2(e) is the error distribution based on NDVITM, and 2(f) is the error distribution based on BPNN (input data are spectral features), and 2(g) is the error distribution based on BPNN (input data are spectral and texture features), and 2(h) is the error statistics based on NDVITM, and 2(i) is the error statistics based on BPNN (input data are spectral features) and 2(j) is the error statistics based on BPNN (input data are spectral and texture features).
|
Download:
|
|
Fig. 2 Results of retrieval of emissivity and the error |
|
After several trials, compared to MODIS emissivity product, the retrieval result based on BPNN method is better than NDVITM and the average error of BPNN and NDVITM is approximately 0.002 and 0.008 respectively. The result of BPNN whose training sets contain texture and spectral features is better. The detailed comparison is shown in Table 1. The computational complexity of GLCM is O(M×N), where M and N is the size of patch. We carried out the experiment using MATLAB on a 3.2 GHz machine with 12 G RAM and i5-3470 CPU. The training process takes 122 s.
|
|
Table 1 Retrieval error based on BPNN and NDVITM |
This paper uses the BPNN method and NDVITM to retrieve surface emissivity from MODIS image and tests the trained BPNN. By comparing different approaches, we find that the accuracy of the BPNN is better than NDVITM and the retrieval results are acceptable. Analysis indicates that the average error of the BPNN is approximately 0.002, and training sets containing texture features can improve the retrieval results. The contributions of this paper lie in the following three aspects: 1) it provides possibility of using abundant available reflectance data to retrieve emissivity map in different scale and spatial resolution; 2) the method does not need to categorize the land cover and the retrieval result is precise; 3) it builds a direct relationship between reflectance data and emissivity data, and provides the possibility of obtaining precise emissivity data through the satellite with a thermal infrared channel. However, at present, we lack emissivity sets of high spatial resolution to train the BPNN. Besides, a new requirement to use as little training sets as possible to achieve a good performance of BPNN module is put forward.
| [1] |
Song J H, Chen S B, Sun K, et al. Visualization to surface temperature retrieval using matlab[J]. Microcomputer Information, 2008, 24:132.
|
| [2] |
BOREL C. Error analysis for a temperature and emissivity retrieval algorithm for hyperspectral imaging data[J]. International Journal of Remote Sensing Remote, 2008, 29(17/18):5029–5045.
|
| [3] |
Caselles V. Thermal remote sensing of land surface temperature from satellites:current status and future prospects[J]. Remote Sensing Reviews, 1995, 12(3):175–224.
|
| [4] |
JiménezMuñoz J C, Sobrino J A. A generalized single channel method for retrieving land surface temperature from remote sensing data[J]. Journal of Geophysical Research, 2003, 108(D22):2015–2023.
|
| [5] |
Islam T, Hulley G C, Malakar N K, et al. A physics-based algorithm for the simultaneous retrieval of land surface temperature and emissivity from VIIRS thermal infrared data[J]. IEEE Trans Geosci Remote Sens, 2017, 108(1):563–576.
|
| [6] |
Qian Y G, Wang N, Ma L L, et al. Evaluation of temperature and emissivity retrieval using spectral smoothness method for low-emissivity materials[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9:4307–4315.
DOI:10.1109/JSTARS.2016.2522464 |
| [7] |
Emami H, Safari A, Mojaradi B. Fusion methods for land surface emissivity and temperature retrieval of the landsat data continuity mission data[J]. IEEE Trans Geosci Remote Sens, 2016, 54:3842–3855.
DOI:10.1109/TGRS.2016.2529422 |
| [8] |
Zhang X, Ding F, Peng X, et al. Fast retrieval of land surface emissivity from landsat data through IDL programming[C]//2014 Third International Workshop on Earth Observation and Remote Sensing Applications (EORSA). IEEE, 2014: 76-80.
|
| [9] |
Wang N, Wu H, Nerry F, et al. Temperature and emissivity retrievals from hyperspectral thermal infrared data using linear spectral emissivity constraint[J]. IEEE Trans Geosci Remote Sens, 2011, 49:1291–1303.
DOI:10.1109/TGRS.2010.2062527 |
| [10] |
Huang Q N, Guo H D, Xi X H et al. Improved method of land surface emissivity retrieval from Landsat TM/ETM+data[C]//2012 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2012: 4206-4208.
|
| [11] |
Gillespie A, Rokugawa S, Matsunaga T, et al. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (ASTER) images[J]. IEEE Trans Geosci Remote Sens, 2002, 36(4):1113–1126.
|
| [12] |
Sobrino J A, Oltra-Carrió R, Jiménez-Muñoz J C, et al. Emissivity mapping over urban areas using a classification-based approach:application to the dual-use european security IR experiment (DESIREX)[J]. International Journal of Applied Earth Observation and Geoinformation, 2012, 18(1):141–147.
|
| [13] |
Caicedo J P R, Verrelst J, Munoz-Mari J, et al. Toward a semiautomatic machine learning retrieval of biophysical parameter[J]. IEEE Journal of Selected Topics in Applied Earth Observation and Remote Sensing, 2014, 7(4):1249–1259.
DOI:10.1109/JSTARS.4609443 |
| [14] |
Mao K B, Tang H J, Li L Y, et al. An NN algorithm for retrieving land surface temperature and emissivity from MODIS data[J]. Remote Sensing Information, 2007(4):9–15.
|
| [15] |
Mao K B, Shi J C, Tang H J, et al. A neural network technique for separating land surface emissivity and temperature from ASTER imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1):200–208.
DOI:10.1109/TGRS.2007.907333 |
| [16] |
Wang N. Simultaneous retrieval of land surface temperature, emissivity and atmospheric profiles from hyperspectral thermal infraed data[D]. Beijing: University of Chinese Academy of Sciences, 2011.
|
| [17] |
Xiong X, Wenny B N, Barnes W D. Overview of NASA earth observing systems terra and aqua moderate resolution imaging spectroradiometer instrument calibration algorithms and on-orbit performance[J]. Remote Sens, 2009, 3.
|
| [18] |
Oltra-Carrió R, Sobrino J A, Franch B, et al. Land surface emissivity retrieval from airborne sensor over urban areas[J]. Remote Sensing of Environment, 2012, 123:298–305.
DOI:10.1016/j.rse.2012.03.007 |
| [19] |
Musci M, Feitosa R Q, Costa G A O P, et al. Assessment of binary coding techniques for texture characterization in remote sensing imagery[J]. IEEE Geosci Remote Sens Letters, 2013, 10(6):1607–1611.
DOI:10.1109/LGRS.2013.2267531 |
| [20] |
Devi K, Gupta P, Grover D, et al. An effective texture feature extraction approach for iris recognition system[C]//20162nd International Conference on Advances in Computing, Communication, & Automation. 2016: 1-5.
|
| [21] |
Yang P P, Hou Z T, Liu X L, et al. Texture feature extraction of mountain economic forest using high spatial resolution remote sensing images[C]//2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). IEEE, 2016: 3156-3159.
|
| [22] |
Edgar A. Corzo M, Arthur A N. Side scan sonar images attributes characterization for seabed mapping[C]//2015 IEEE/OES Acoustics in Underwater Geosciences Symposium (RIO Acoustics). de Janeiro: IEEE, 2015: 1-4.
|
 2018, Vol. 35
2018, Vol. 35 


