2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
外辐射源雷达本身不发射电磁波,通过被动接收目标或第三方发射的电磁信号,对目标进行定位及跟踪,具有隐蔽性强、成本低、抗干扰能力强等诸多优点,因此成为各国的研究热点[1-4]。由于外辐射源信号为非合作雷达信号,要从含有直达波多径、杂波及噪声的回波中检测出微弱的目标回波信号,信号处理首先要对消掉直达波和杂波,然后对回波和参考信号进行长时间相参积累。在外辐射源雷达双基/多基模型下,目标径向运动引起距离徙动,目标切向运动以及本身的加速度引起多普勒徙动,严重影响积累增益。目前,雷达图像中的keystone方法[5]可很好地用来解决外辐射源雷达中的距离徙动问题,但多普勒徙动问题仍在研究阶段。
针对多普勒徙动问题,现有典型方法主要有线性调频信号的检测方式,如分数阶傅里叶变换[6]、WVD-Hough变换[7]及离散多项式相位变换[8]等,另外还有两次短傅里叶变换的徙动补偿[9],无需搜索调频率的sandglass[10-11]等方法。以上现有方法所需的计算量大,实现较困难,且不适用于多目标场景。双频共轭方法一开始的提出是为了解决ISAR中高速运动目标的多普勒模糊问题,进而更好地对目标进行Keystone距离徙动校正,其原理是使合成信号的波长大大增加,降低目标多普勒。本文针对外辐射源双基雷达下目标的多普勒徙动问题,引入双频共轭[12]处理方法,可有效校正多普勒徙动,提高目标积累增益。这种方法便于实时实现,并适用于多目标场景。
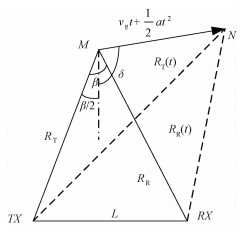
1 外辐射源雷达回波信号模型此处我们讨论的外辐射源雷达模型为双基模型。在对信号进行相参积累的过程中,双基模型和目标本身的运动状态会带来目标时延的相应变化。除产生初始距离单元、多普勒频率以外,还会产生距离徙动和多普勒徙动。目标运动的回波模型如图 1所示。将目标的三维速度投影到双基地平面上进行研究,β为双基地角,TX是信号发射站,RX是信号接收站,发射站和接收站均静止,L为发射站和接收站之间的基线距离,令目标初始位置为M,RT和RR分别表示目标与发射站和接收站之间的距离。假设目标直线运动,初始投影速度为vg,加速度为a,其中当a=0时目标匀速直线运动,t时刻目标运动到N位置,δ为目标运动方向与双基地角平分线的夹角。
|
Download:
|
| 图 1 外辐射源雷达双基模型图 Fig. 1 Bistatic setup of passive radar | |
t时刻时,目标的运动距离MN为
| $ \left\{ \begin{array}{l} {R_{\rm{T}}}\left( t \right) = \sqrt {R_{\rm{T}}^2 + R_v^2\left( t \right) - 2{R_{\rm{T}}}{R_v}\left( t \right)\cos \left( {\delta - \frac{\beta }{2}} \right)}, \\ {R_{\rm{R}}}\left( t \right) = \sqrt {R_{\rm{R}}^2 + R_v^2\left( t \right) - 2{R_{\rm{R}}}{R_v}\left( t \right)\cos \left( {\delta + \frac{\beta }{2}} \right)} . \end{array} \right. $ | (1) |
将上面二式分别在t=0处进行Taylor展开,并忽略二次以上项,可得瞬时双基地距离R(t)
| $ \begin{array}{l} R\left( t \right) = {R_{\rm{T}}}\left( t \right){\rm{ + }}{R_{\rm{R}}}\left( t \right) \approx \\ \;\;{R_{\rm{T}}} - {v_g}t\cos \left( {\delta - \frac{\beta }{2}} \right) + \\ \;\;\frac{1}{2}\left( {\frac{{v_g^2{{\sin }^2}\left( {\delta - \beta /2} \right)}}{{{R_{\rm{T}}}}} - a\cos \left( {\delta - \frac{\beta }{2}} \right)} \right){t^2} + \\ \;\;{R_{\rm{R}}} - {v_g}t\cos \left( {\delta + \frac{\beta }{2}} \right) + \\ \;\;\frac{1}{2}\left( {\frac{{v_g^2{{\sin }^2}\left( {\delta + \beta /2} \right)}}{{{R_{\rm{R}}}}} - a\cos \left( {\delta + \frac{\beta }{2}} \right)} \right){t^2}. \end{array} $ | (2) |
设s(t)为参考直达波,信号载频为f0,则外辐射源雷达系统中运动目标的回波信号模型可以表示为
| $ \begin{array}{l} {y_{\rm{r}}}\left( t \right) = {A_0}s\left( {t - \frac{{R\left( t \right) - L}}{c}} \right){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_0}\left( {\frac{{R\left( t \right) - L}}{c}} \right)}}\\ \;\;\;\;\;\;\;\; = {A_0}s\left( {t - {\tau _0} - \tau \left( t \right) - \tau \left( {{t^2}} \right)} \right){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\left( {{\tau _0} + \tau \left( t \right) + \tau \left( {{t^2}} \right)} \right)}}, \end{array} $ | (3) |
式中:A0为幅度常数,τ0、τ(t)、τ(t2)分别是关于t的常数项、一次项和二次项,即:
| $ \begin{array}{l} {\tau _0} = \frac{{{R_{\rm{T}}} + {R_{\rm{R}}} - L}}{c}, \\ \tau \left( t \right) = \frac{{ - 2{v_g}\cos \delta \cos \left( {\frac{\beta }{2}} \right)t}}{c}\\ \tau \left( {{t^2}} \right) = \frac{1}{{2c}}\left[{v_g^2} \right.\left( {\frac{{{{\sin }^2}\left( {\delta-\beta /2} \right)}}{{{R_{\rm{T}}}}} + \frac{{{{\sin }^2}\left( {\delta + \beta /2} \right)}}{{{R_{\rm{R}}}}}} \right)-\\ \;\;\;\;\;\;\;\;\;\;\left. {2a\cos \delta \cos \left( {\frac{\beta }{2}} \right)} \right]{t^2}. \end{array} $ | (4) |
经keystone方法校正完距离徙动后,回波信号模型为
| $ \begin{array}{l} {y_{\rm{r}}}\left( t \right) = {A_0}s\left[{t-{\tau _0}} \right]{{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}{f_{{d^t}}}}}{{\rm{e}}^{{\rm{-j \mathsf{ π} }}{\alpha _{{{\rm{d}}^{{t^2}}}}}}}, \\ \end{array} $ | (5) |
式中:A0为幅度常数;回波时延中常数项τ0由式(4)给出;多普勒频率
| $ \begin{array}{l} {\alpha _{\rm{d}}} = \left( {v_g^2} \right.\left( {\frac{{{{\sin }^2}\left( {\delta - \beta /2} \right)}}{{{R_{\rm{T}}}}} + \frac{{{{\sin }^2}\left( {\delta + \beta /2} \right)}}{{{R_{\rm{R}}}}}} \right) - \\ \;\;\;\;\;\;\;\left. {\;2\;a\cos \delta \cos \left( {\frac{\beta }{2}} \right)} \right)/\lambda . \end{array} $ |
其中λ为信号波长。因此可以得出:回波信号的多普勒频率徙动量与调频率αd有直接关系,即分别与信号波长λ、速度vg、加速度a、回波模型RT、RR、δ、β等有关。当目标有切向速度或者目标没有切向速度但本身有加速度时,都会产生多普勒徙动。例如,当工作频率为674 MHz,匀速运动目标径向速度为5.66 m/s,切向速度为350 m/s,单基距离在150 km时,调频率αd为3.26 Hz/s,对应1 s积累时间的增益损失约4.5 dB,对应5 s积累时间的增益损失约12 dB.
因此,在对回波信号进行长时间相参积累时,解决多普勒徙动问题是非常有必要的,故在下一节引入双频共轭[12]处理方法。
2 双频共轭处理算法双频共轭方法(SDCFCP)如下:
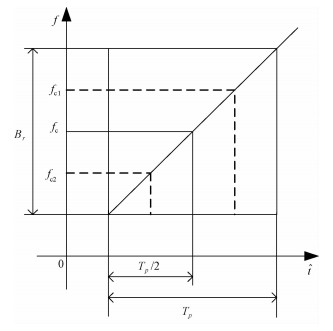
其原理如图 2所示,将外辐射源雷达接收的回波信号二维分时处理,得到距离向、方位向数据,我们将距离向信号近似看成LFM信号,平分成2个子带信号。
|
Download:
|
| 图 2 双频共轭原理图 Fig. 2 Schematic of SDCFCP | |
在图 2中,Br为原信号的带宽,fc为中心频率,Tp为时宽,2个子带信号的中心频率差为|fc1-fc2|=Br/2,二者带宽也均为Br/2。分别对这2个信号进行距离压缩,得到运动目标的距离向为
| $ \begin{array}{l} {s_{Rl}}\left( {\hat t, {t_m}} \right) = \sum\limits_{n = 1}^N {{A_n}} \sin c\left( {\frac{{{B_r}}}{2}\left( {\hat t - \frac{{{R_n}\left( {{t_m}} \right) - L}}{c}} \right)} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}{f_{cl}}\frac{{{R_n}\left( {{t_m}} \right) - L}}{c}} \right). \end{array} $ | (6) |
式中:
| $ {s_m}\left( {\hat t, {t_m}} \right) = {s_{R2}}\left( {\hat t, {t_m}} \right){\rm{conj}}\left( {{s_{R1}}\left( {\hat t, {t_m}} \right)} \right). $ | (7) |
显然,式(7)为一多项式,由目标上各个散射点信号的自身项和交叉项组成。由于2个子带信号的时差通常仅在微秒量级,在此期间目标的运动远远小于一个距离分辨单元,所以可认为目标的距离向是对准的。同时,不同目标信号组成的交叉项中,由于目标间的双基距离通常大于一个距离分辨单元,因此交叉项的幅值就远远小于自身项,式(7)中的交叉项就可忽略,尤其是在分辨率较高的情况下。所以,这种方法可以很好的适用于多目标场景。
基于上述分析,再对合成信号幅值开方,将功率量纲调整为电压量纲,则式(7)可转化为
| $ \begin{array}{l} {s_m}\left( {\hat t, {t_m}} \right) \approx \sum\limits_{n = 1}^N {{A_n}} \left| {\sin c\left( {\frac{{{B_r}}}{2}\left( {\hat t - \frac{{{R_n}\left( {{t_m}} \right) - L}}{c}} \right)} \right)} \right|\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - {\rm{j}}2{\rm{ \mathsf{ π} }}\left( {{f_{{\rm{c}}2}} - {f_{{\rm{c}}1}}} \right)\frac{{{R_n}\left( {{t_m}} \right) - L}}{c}} \right). \end{array} $ | (8) |
此时,式(8)所示的合成信号的中心频率为两子带信号中心频率之差,则合成信号中目标各散射点的多普勒中心频率为
| $ {f'_{dn}} = \frac{{2\left( {{f_{{\rm{c}}1}} - {f_{{\rm{c}}2}}} \right){v_g}}}{c}\cos \delta \cos \left( {\frac{\beta }{2}} \right). $ | (9) |
结合式(4),二次项调频率为
| $ {{\alpha '}_{\rm{d}}} = 2\left( {{f_{{\rm{c}}1}} - {f_{{\rm{c}}2}}} \right)\frac{{{r_2}}}{c}. $ | (10) |
通常情况下,有fc2-fc1<<fc,则可有
| $ {{f'}_{dn}} \ll {f_{dn}} = \frac{{2{f_{\rm{c}}}{v_g}}}{c}\cos \delta \cos \left( {\frac{\beta }{2}} \right), $ | (11) |
| $ {{\alpha '}_{\rm{d}}} < {\alpha _{\rm{d}}} = \frac{{2{f_{\rm{c}}}{r_2}}}{c}. $ | (12) |
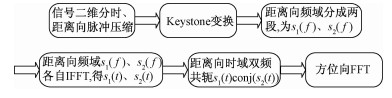
由此可见,该处理使合成信号的等效波长大大增加,使得合成信号中目标的多普勒中心频率和二次项调频率都趋于零,即将方位向的多普勒徙动量和副瓣都压得很低,从而提升相参积累后的目标信噪比。由于该方法只是在距离向多了一个共轭相乘的步骤,并没有提升二维分时处理的计算复杂度,因此该方法计算量非常小,这是之前一些多普勒徙动补偿算法[6-8]都不具备的优势。并且上文已经分析出共轭相乘后目标间的交叉项非常小,所以该方法同样适用于多目标场景。对于数字电视信号,带宽约8 MHz,双频共轭方法通过距离向共轭相乘的方式,解决长时间相参积累中动目标的多普勒徙动问题,提升目标信噪比。当然,由于双频共轭方法将信号分为等带宽的2个子带信号进行双频共轭处理,相比于原始信号,理论上目标增益会有3 dB的固定损失。具体实现流程如图 3所示。
|
Download:
|
| 图 3 双频共轭处理流程图 Fig. 3 Flowchart of SDCFCP processing | |
对回波(杂波对消后)和参考信号进行二维分时处理,距离向实现脉冲压缩,进而联合方位向进行keystone变换,完成距离徙动校正;然后在距离向将信号分成频域的两段数据,完成双频共轭处理,最终再进行方位向傅里叶变换,从而完成相参积累。
在应用双频共轭方法时,也发现如果运动目标积累前的输入信噪比非常低,该方法会受到限制。因为噪声成分比较大时,会影响到距离向数据的相位信息,进而影响双频共轭的效果。考虑到双频共轭方法已经等效于压低了方位向副瓣,因此,当目标处于低多普勒域,即目标切向飞行速度很大时,可通过增加距离向数据长度(即降低等效PRF)的方式,继续降低距离向脉冲压缩副瓣,进一步提高目标信噪比,这种改进方式可改善双频共轭处理的性能。后文中的数据处理也证明了该种方式的有效性。
但是经过分析和仿真得知,当目标输入信噪比非常低时,双频共轭处理方法会失效。如处理输入信噪比为-57 dB、带有多普勒徙动目标的5 s数据,运用双频共轭方法不能提高目标信噪比。
3 仿真和实测数据分析前文中已对多普勒徙动造成的能量损失问题进行了分析,并提出了解决方法,本节重点通过仿真和实测数据验证了该算法的有效性。
3.1 仿真分析结合实际场景,设检测系统虚警率为10-6,发现概率为0.8,对应最小检测因子为13 dB。基于DTTB数字电视信号单载波模式(信号带宽8 MHz,采样率8 MHz),首先仿真3个运动目标,仿真参数见表 1。
|
|
表 1 仿真参数(多普勒范围-200~200 Hz) Table 1 Simulation parameters (Doppler -200~200 Hz) |
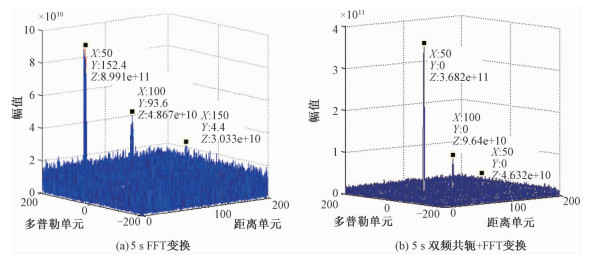
分别对5 s的仿真数据(包含目标1、2、3,没有加入距离徙动)做直接FFT变换,以及对5 s数据做双频共轭和FFT变换,仿真结果如图 4(a)、图 4(b)所示,信噪比如表 2所示。
|
Download:
|
| 图 4 目标仿真对比图 Fig. 4 Comparison chart for simulation target | |
|
|
表 2 仿真目标信噪比 Table 2 SNR of simulation target |
对比图 4、表 2中的2组仿真结果,目标1、2、3的信噪比通过双频共轭方法,均得到提升,因此该方法可很好地解决同一场景下多个运动目标的多普勒徙动问题。并且,对于目标1,5 s数据经过FFT变换处理,目标信噪比为12.6 dB,低于检测因子,系统很难检测到该目标,但加入双频共轭处理操作,信噪比提升到14.4 dB,目标可以被检测到。
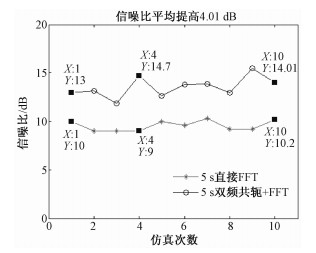
同时,当运动目标输入信噪比比较低,多普勒频率处在低多普勒域时,可通过加长二维分时的距离向数据长度(即改变重频PRF),进行双频共轭处理。对于仿真目标1,设输入信噪比为-54 dB,二维分时的多普勒频率范围设为-24~24 Hz。分别对目标1的5 s数据(没有加入距离徙动)做直接FFT变换,以及对目标1做双频共轭和FFT变换,多次仿真信噪比结果如图 5所示。
|
Download:
|
| 图 5 低信噪比目标仿真结果图 Fig. 5 Simulation result for low SNR target | |
由图 5可以看出,当目标1输入信噪比为-54 dB时,对5 s数据进行PRF压缩和双频共轭系列处理,积累信噪比从10 dB提高到14 dB,系统可以检测到该目标,其检测能力得到较大的改善。
3.2 实测数据分析本节采用基于DTTB数字电视信号一组实测数据进行实验分析。实测数据的主要相关参数如表 3所示。
|
|
表 3 实测数据相关参数 Table 3 Experiment parameters |
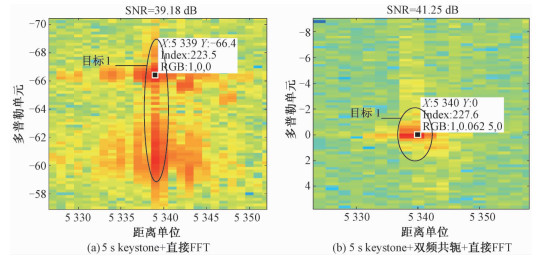
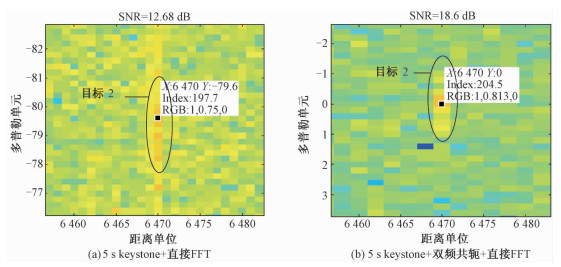
以下是一组实测数据处理图:对5 s的实测数据分别进行常规方法处理(5 s keystone变换+直接FFT)和加入双频共轭方法的处理(5 s keystone变换+双频共轭+直接FFT),数据中有多个目标,在此选取其中2个,实测对比结果如图 6、图 7所示。
|
Download:
|
| 图 6 实测目标1对比图 Fig. 6 Comparison result for experimental target 1 | |
|
Download:
|
| 图 7 实测目标2对比图 Fig. 7 Comparison result for experimental target 2 | |
目标1:双基距离160 km,多普勒-60 Hz,
目标2:距离194 km,多普勒-88 Hz。
从图 6和图 7中可以明显看出,经过双频共轭处理,目标由原来多普勒维散焦多个单元,变化到能很好地聚焦到零多普勒附近。目标1和目标2经过双频共轭系列处理,信噪比均得到提高。同时,当目标2只采用keystone+直接FFT处理时,信噪比低于检测因子13 dB,无法被系统检测出,加入双频共轭后,信噪比升到18.6 dB,高于检测因子,该目标重新被检测到。
由此可见,双频共轭算法可以解决多目标的多普勒徙动问题,提高检测目标。
4 结论本文从外辐射源雷达双基模型出发,推导目标运动时多普勒徙动的产生原因,随之提出双频共轭处理方法解决该问题,通过该方法提高目标积累信噪比,改善系统探测能力,同时对于切向速度较大的微弱目标,采取压缩方位向重频的方式,进一步改善双频共轭方法性能,提高目标增益。通过仿真分析和实测数据验证了该方法的有效性,算法无需依赖目标的先验信息,适用于多目标场景,计算量小,适于实时处理,是一种实时高效的高切向速度目标检测方法。但由于处理信噪比非常低的目标时,双频共轭方法应用会受到限制,因此,如何提高非常微弱的目标的探测能力,将是下一步工作重点。
| [1] |
Griffiths H. Developments in bistatic and networked radar[C]//Radar(Radar), 2011 IEEE CIE International Conference on Radar, 2011, 1: 10-13.
|
| [2] |
Griffiths H D, Baker C J. Passive coherent location radar systems. Part 1:performance prediction[J]. IEE Proceedings-Radar Sonar & Navigatio, 2005, 152(3):153–159.
|
| [3] |
Howland P. Editorial:passive radar systems[J]. IEE Proceedings-Radar Sonar and Navigation, 2005, 152(3):105–106.
DOI:10.1049/ip-rsn:20059064 |
| [4] |
陶然, 王越, 单涛, 等. 分布式无源检测信息系统研究进展[J]. 深圳大学学报(理工版), 2004, 21(2):101–106.
|
| [5] |
关欣, 胡东辉, 仲利华, 等. 一种高效的外辐射源雷达高径向速度目标实时检测方法[J]. 电子与信息学报, 2013, 35(3):581–588.
|
| [6] |
杨金禄, 单涛, 陶然. 数字电视辐射源雷达的相参积累徙动补偿方法[J]. 电子与信息学报, 2011, 33(2):407–411.
|
| [7] |
关欣, 仲利华, 胡东辉, 等. 一种基于RSPWVD-Hough变换的无源雷达多普勒展宽补偿方法[J]. 雷达学报, 2013, 2(4):430–438.
|
| [8] |
庞存锁. 基于离散多项式相位变换和分数阶傅里叶变换的加速目标检测算法[J]. 电子学报, 2012, 40(1):184–188.
|
| [9] |
Hoshino T, Suwa K, Nakamura S, et al. Long-time integration by short-time cross-correlation and two-step Doppler processing for Passive Bistatic Radar[C]//Radar Conference, 2013, 1552(1): 451-454.
|
| [10] |
Liu Y, Xing M, Guo R, et al. Sandglass transformation for synthetic aperture radar detection and imaging of ship at low signal-to-clutter-plus-noise ratio[J]. Iet Radar Sonar Navigation, 2011, 5(3):361–373.
DOI:10.1049/iet-rsn.2010.0028 |
| [11] |
战立晓, 汤子跃, 朱振波. 一种米波相控阵雷达四代机目标检测算法[J]. 电子与信息学报, 2013, 35(5):1163–1169.
|
| [12] |
Jian-Fen Y, Dao-Jing L, Li-Bo T, et al. Detection and imaging of aerial moving targets based on spaceborne SAR[C]//International Conference on Radar, 2006: 1-5.
|
 2018, Vol. 35
2018, Vol. 35 


