2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
极化SAR具备全天时、全天候的数据获取能力,与单极化SAR相比,它提供了更完整的目标后向散射信息[1]。建筑提取是遥感图像解译的关键问题之一,并在灾害评估[2]、城市规划、人口估计等方面都得到广泛的应用[3]。目前国内外学者关于极化SAR的建筑提取问题已开展了很多研究,文献[4]提出一种扩展四分量分解算法,使用非监督kmeans聚类将建筑和背景分离开来;文献[5]综合利用极化SAR图像的极化特征和纹理特征,并通过交叉分类提高了提取准确率;文献[6]利用目标散射矢量模型TSVM生成旋转不变极化参数组合,进而用于提取城市区域典型人工地物。通常在实际应用中,多种特征参数组合要比单一特征更能准确地描述地物目标,然而特征与特征之间存在冗余度与相关性,难以直接辨别哪些特征在分类过程中起到较为重要的作用,而哪些特征是无关紧要可以去除的[7]。另外,一些典型的分类器如神经网络[8]、支持向量机[9]、随机森林[10]等已经成功应用到极化SAR图像解译中,但是单个分类器往往不能满足实际需求,学者们开始尝试构建多分类器系统[11]。
考虑到上述问题,本文提出一种基于特征筛选和二级分类的提取算法。该方法首先从极化SAR数据中提取出常用的16维特征;然后利用随机森林进行初级分类和特征筛选;最后用支持向量机对筛选后的特征子集进行次级分类,并用邻域投票法将两级分类结果融合后得到最终结果。一方面避免了单一特征对地物特性描述不足,另一方面利用特征筛选降低了计算复杂度;另外,通过融合两级不同类型分类器的结果,在提高准确率的同时保持了空间一致性。
1 算法原理 1.1 极化SAR特征描述散射回波具有相干性的目标可以用极化散射矩阵S完全描述,然而在实际动态变化的环境中,测量值受相干斑噪声、随机散射效应等的影响,目标表现为非相干目标,常用极化相干矩阵T和极化协方差矩阵C进行描述。
| $\mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}} & {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}}\\ {{\mathit{\boldsymbol{S}}_{{\rm{VH}}}}} & {{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\left| {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}} \right|{{\rm{e}}^{{\rm{j}}{\phi _{{\rm{HH}}}}}}} & {\left| {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}} \right|{{\rm{e}}^{{\rm{j}}{\phi _{{\rm{HV}}}}}}}\\ {\left| {{\mathit{\boldsymbol{S}}_{{\rm{VH}}}}} \right|{{\rm{e}}^{{\rm{j}}{\phi _{{\rm{VH}}}}}}} & {\left| {{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \right|{{\rm{e}}^{{\rm{j}}{\phi _{{\rm{VV}}}}}}} \end{array}} \right],$ | (1) |
| $\mathit{\boldsymbol{T}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\left\langle {{{\left| {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}} + {\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \right|}^2}} \right\rangle } & {\left\langle {({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} + {\mathit{\boldsymbol{S}}_{{\rm{VV}}}}){{({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} - {\mathit{\boldsymbol{S}}_{{\rm{VV}}}})}^*}} \right\rangle } & {2\left\langle {({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} + {\mathit{\boldsymbol{S}}_{{\rm{VV}}}})\mathit{\boldsymbol{S}}_{{\rm{HV}}}^*} \right\rangle }\\ {\left\langle {({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} - {\mathit{\boldsymbol{S}}_{{\rm{VV}}}}){{({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} + {\mathit{\boldsymbol{S}}_{{\rm{VV}}}})}^*}} \right\rangle } & {\left\langle {{{\left| {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}} - {\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \right|}^2}} \right\rangle } & {2\left\langle {({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} - {\mathit{\boldsymbol{S}}_{{\rm{VV}}}})\mathit{\boldsymbol{S}}_{{\rm{HV}}}^*} \right\rangle }\\ {2\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}{{({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} + {\mathit{\boldsymbol{S}}_{{\rm{VV}}}})}^*}} \right\rangle } & {2\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}{{({\mathit{\boldsymbol{S}}_{{\rm{HH}}}} - {\mathit{\boldsymbol{S}}_{{\rm{VV}}}})}^*}} \right\rangle } & {4\left\langle {{{\left| {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}} \right|}^2}} \right\rangle } \end{array}} \right]$ | (2) |
| $\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {\left\langle {{{\left| {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}} \right|}^2}} \right\rangle } & {\sqrt 2 \left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}\mathit{\boldsymbol{S}}_{{\rm{HV}}}^*} \right\rangle } & {\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}\mathit{\boldsymbol{S}}_{{\rm{VV}}}^*} \right\rangle }\\ {\sqrt 2 \left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}\mathit{\boldsymbol{S}}_{{\rm{HH}}}^*} \right\rangle } & {2\left\langle {{{\left| {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}} \right|}^2}} \right\rangle } & {\sqrt 2 \left\langle {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}\mathit{\boldsymbol{S}}_{{\rm{VV}}}^*} \right\rangle }\\ {\left\langle {{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}\mathit{\boldsymbol{S}}_{{\rm{HH}}}^*} \right\rangle } & {\sqrt 2 \left\langle {{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}\mathit{\boldsymbol{S}}_{{\rm{HV}}}^*} \right\rangle } & {\left\langle {{{\left| {{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \right|}^2}} \right\rangle } \end{array}} \right].$ | (3) |
式(2)和式(3)中,〈·〉表示时间或空间集合平均,*表示复数矩阵的共轭转置,并假设随机媒质是各向同性的。极化SAR系统测量的散射总功率称为Span,它反映回波的强度,通常将其定义为
| $\begin{array}{l} {\rm{Span}} = {\rm{Tr}}\left( {\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{S}}^{*{\rm{T}}}}} \right) = {\left| {{\mathit{\boldsymbol{S}}_{{\rm{HH}}}}} \right|^2} + 2{\left| {{\mathit{\boldsymbol{S}}_{{\rm{HV}}}}} \right|^2} + {\left| {{\mathit{\boldsymbol{S}}_{{\rm{VV}}}}} \right|^2}\\ \quad \quad = {T_{11}} + {T_{22}} + {T_{33}} = {C_{11}} + {C_{22}} + {C_{33}}. \end{array}$ | (4) |
影响建筑SAR回波的主要因素有雷达系统参数(如波长、极化方式、入射角和观测方向等)、建筑物表面特性(如粗糙度、复介电常数、几何结构等)和环境变量(如地形起伏)等[12],极化SAR中建筑目标的各种特性就是这些因素相互作用的结果。在电磁波的照射下,建筑区域发生的散射主要有屋顶的镜面反射、地面与墙面的二次散射、复杂墙面结构的多次散射等,另外,SAR成像几何畸变会引起叠掩、阴影和角反射器效应,这导致建筑区域内部存在大量由角反射器强反射产生的亮斑和由叠掩效应产生的亮线,而亮斑和亮线之间夹杂着较暗的阴影,形成具有一定规律的纹理[13]。基于以上原因,本文从极化功率强度、散射机制、纹理变化的角度入手,选择一些代表性特征对极化SAR数据中的建筑目标进行描述,具体包括:直接测量到的极化数据、基于特征矢量的H/α/A分解特征[14]、基于散射模型的Yamaguchi分解特征[15]、基于灰度共生矩阵的统计量纹理特征[16]和半方差函数纹理特征[17],它们都是应用于建筑提取的典型特征[5, 9, 18],具体如表 1所示。
|
|
表 1 特征集合 Table 1 Feature set |
其中,直接测量到的极化数据包括极化散射总功率Span和极化相干矩阵T的对角线元素T11、T22、T33,Span反映极化SAR系统的回波强度,T11表示目标对称因子,T22表示目标非对称因子,T33表示目标非规则因子。利用H/α/A分解可得到极化散射熵H,极化散射角α和各向异性度A这3个参数,其中极化散射熵H表示散射媒质从各向同性散射(H=0)到完全随机散射(H=1)的随机性;散射角α与平均物理散射机制直接相关,对应着从表面散射α=0°到体散射α=45°再到二面角散射α=90°的变化;各向异性度A描述由特征分解得到的第2个和第3个特征值的相对大小,以上3个参数均具有旋转不变性。从Yamaguchi四分量分解中,可以得到表面散射分量PS、二次散射分量PD、体散射分量PV以及螺旋散射分量PH,与Freeman-Durden三分量分解相比引入了建筑目标中存在的螺旋散射机制,可以更好地区分建筑与背景。由灰度共生矩阵可推导出多种统计参数,本文选择其中4种作为纹理特征,包括熵、对比度、同质性和均值。其中熵ENT代表图像信息量的随机性,熵最大时图像也最复杂;对比度CON反映图像的清晰度和纹理的沟纹深浅,对比度越大则图像越清晰;同质性HOM体现图像局部均匀程度,若图像纹理的不同区域间变化较小,则其值大,说明局部非常均匀;均值MEN反映纹理的规则程度,纹理杂乱无章的、难以描述的,值较小,而纹理规律性强的均值较大。半方差函数V描述像素与邻域像素的灰度相关性,被认为是建筑分类性能较好的纹理特征[19],因此本文将其作为建筑提取的纹理特征之一。
1.2 分类器设计随机森林(random forest,简称RF)是用Bagging方法将多棵CART决策树集成在一起的分类器。它在Bagging随机样本选择的基础上引入随机特征选择,即随机且有放回地从训练集中抽取N个训练样本作为一棵决策树的训练集,并且随机从M个特征中选取m个构成特征子集,每次树进行分裂时都会从这m个特征中选择最优的。以上两个随机性使得随机森林的泛化性能可通过决策树之间差异度的提升而增加,最终的预测结果由所有决策树的分类结果投票决定。随机森林分类器有一个重要性质:能够计算单个特征变量的重要性,进而从所有特征中选择出相对重要的特征[20]。
利用随机森林评估某个特征X的重要性方法如下:
1) 对于每一棵决策树, 使用相应的OOB(out of bag,袋外数据)计算它的袋外数据误差, 记为errOOB1;
2) 随机地对袋外数据所有样本的特征X加入噪声干扰,再次计算它的袋外数据误差, 记为errOOB2;
3) I(X)=∑(errOOB2-errOOB1)/NTree,其中I(X)为特征X的重要性值,NTree为决策树数目。
若给某个特征随机加入噪声后,袋外误差大幅度增大,则说明这个特征对于样本的分类结果影响很大,即重要程度相对较高。对随机森林中的特征变量按照重要性降序排序,确定删除比例,从当前的特征集合中剔除相应比例不重要的特征,可以得到一个新的特征子集,从而起到特征筛选的作用。
支持向量机(support vector machine,简称SVM)是一种监督学习的方法,已广泛应用于统计分类以及回归分析,其基本模型定义为特征空间上间隔最大的线性分类器,学习策略是间隔最大化,最终可转化为一个凸二次规划问题的求解:
| $\begin{array}{l} \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{w}},b} \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2},\\ {\rm{s}}{\rm{.t}}.\;\;{y_i}({\mathit{\boldsymbol{w}}^{\rm{T}}}{x_i} + b) \ge 1,i = 1,2, \cdots m, \end{array}$ | (5) |
其中,w为权重系数,b为位移项,(xi, yi)为样本集中的训练样本。
在线性不可分的情况下,支持向量机通过核函数将输入变量映射到一个高维特征空间,在这个空间中构造最优分类超平面[21],避免了在原输入空间中进行非线性曲面分割计算。支持向量机的数学理论基础比较完善,可以解决小样本情况下的机器学习问题。
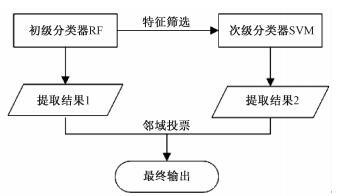
由于随机森林具有特征筛选功能,所以可将其作为初级分类器,在得到分类结果的同时对特征的重要性进行评估,筛选得到新的特征子集。利用支持向量机对特征子集进行次级分类,将两次分类结果通过邻域投票法融合起来,本文的分类器设计如图 1所示。
|
Download:
|
| 图 1 分类器设计图 Fig. 1 Classifier design | |
其中,邻域投票法考虑到像素之间的空间相关信息,当分类结果在像素点(i, j)处不同时,以像素点为中心取一个宽度为width的正方形窗口,统计两级分类结果在窗口内的不同类别的像素数目,将中心像素的类别标记为像素数目最多的类别C
| $C = \mathop {{\rm{max}}}\limits_c \left( {{\rm{SUM}}\left( {E\left( {k,l} \right) = = c} \right)} \right),c = 0,1,$ | (6) |
其中:E=(E1, E2),i-width/2≤k≤i+width/2,j-width/2≤l≤j+width/2,E1为窗口内的初级提取结果,E2为窗口内的次级提取结果。
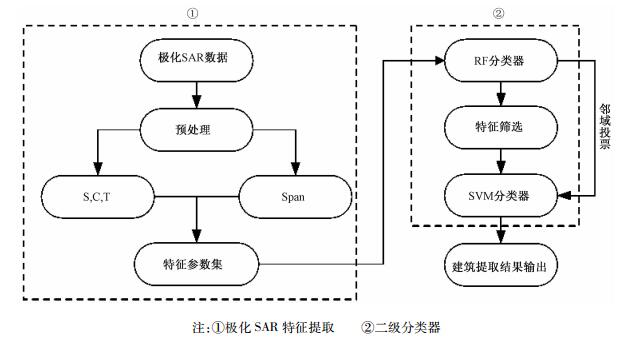
1.3 本文算法步骤本文提出的建筑提取算法流程如图 2所示。由于多维特征之间存在冗余度与相关性,本文提出一种基于特征筛选和二级分类的建筑提取算法框架。该算法的思路是在用随机森林进行初级分类的同时,对各特征的重要性进行评估,筛选出较为重要的特征子集,进而用支持向量机进行次级分类,将两级分类结果用邻域投票法融合给出最终的建筑提取结果。具体由以下6个步骤构成:
|
Download:
|
| 图 2 本文算法流程图 Fig. 2 Flow chart of the algorithm | |
步骤1 输入极化SAR数据,对其进行精致Lee滤波。
步骤2 提取滤波后数据的极化特征和纹理特征,构成维度为M的原始特征参数集X;
步骤3 从极化SAR图像中选择部分标记样本作为训练样本,每个训练样本都可用一个M维特征向量来描述,训练得到RF分类器。用RF分类器对整幅SAR图像进行预测,预测结果为二值图像E1,0代表非建筑,1代表建筑,同时可计算得到各特征的重要性参数,循环10次(由实际情况而定)后获得特征的平均重要性排名VI。
步骤4 设定消除比例F为20%,偏差U为1%。根据VI,每次从原始特征集中去掉重要性最低的ΔM维特征构成新的特征子集X,其中ΔM=floor(M*F),计算对应情况下的RF分类准确率。重复以上“消除-计算”[22]过程直到X为空,选择分类结果与最高准确率偏差在U之内且维度最低的特征子集作为最优特征集合X。消除比例F与偏差U的具体数值都可根据实际情况而定。
步骤5 在最优特征集合X上,用训练得到的SVM分类器重新对整幅SAR图像进行预测,预测结果为二值图像E2。
步骤6 利用邻域投票法将E1和E2融合起来,得到最终的建筑提取结果。
2 实验结果与分析本文选取的实验数据集为美国AIRSAR系统获取的东京八王子市地区的L波段数据[23],相关参数如表 2所示。
|
|
表 2 AIRSAR数据参数 Table 2 AIRSAR data parameters |
该地区的典型地物有4类:建筑、植被、水体和田地,每类地物选择5 400个像素点作为初始训练样本。由于本文关注的是建筑提取效果,所以测试样本只标记两类,即建筑与非建筑。数据的Pauli分解伪彩图、Google earth地物参照图、训练样本标记图和测试样本标记图如图 3所示。

|
Download:
|
| 图 3 AIRSAR极化数据 Fig. 3 AIRSAR polarimetric data | |
混淆矩阵可用于评价分类算法的性能,本文采用由混淆矩阵计算得到的4个评价指标对算法性能进行评估,包括:
1) 准确率:
2) 灵敏度:
3) 召回率:
4) F1值:
其中:TP代表正例样本被正确划分为正例的数目,TN代表负例样本被正确划分为负例的数目,FP代表负例样本被错误划分为正例的数目,FN代表正例样本被错误划分为负例的数目,P代表正例样本数目,N代表负例样本数目。由于灵敏度和召回率有时候会互相矛盾,所以定义F1值为二者的调和平均,准确率和F1值越高,意味着算法的性能越好。
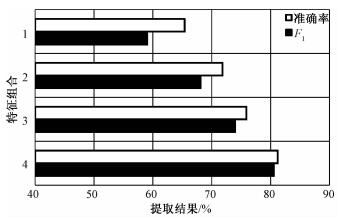
2.1 特征融合为了验证特征融合的有效性,观察算法性能受特征数目及类型的影响,表 3中将多维特征构成不同的特征子集,依次使用随机森林分类器进行建筑提取,实验结果如图 4所示。随着参与分类的特征数目及类别越来越丰富,准确率与F1值越来越高,表示算法性能越来越好。可见多特征融合与单一类型特征相比,有助于提高分类算法性能。
|
Download:
|
| 图 4 不同特征组合对提取结果的影响 Fig. 4 Effect of the combinations of features on extraction results | |
|
|
表 3 不同类型特征组合 Table 3 Different types of feature combinations |
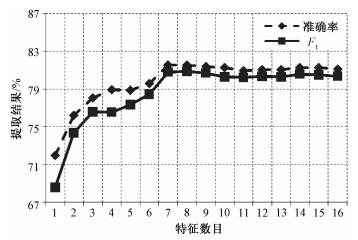
随机森林在分类的同时能够对各个特征的重要性进行评估,按照重要性从高到低的顺序,依次加入特征进行建筑提取实验,准确率和F1值的变化如图 5所示。从图 5中可看出,初期每加入一个特征都能较为明显地提高分类准确率,但是随着特征重要性的降低及特征数目的增加,分类准确率基本保持不变,此时更多的特征意味着算法模型更复杂、计算时间更长,所以有必要进行特征筛选。由于随机森林在分类的同时可以完成特征筛选的工作,并且训练和预测速度快,所以非常适合用作初级分类器,为后续进一步分类提供有效的特征子集。
|
Download:
|
| 图 5 特征数目对提取结果的影响 Fig. 5 Effect of the number of features on extraction results | |
为验证本文算法的有效性,将它与随机森林(RF)算法和支持向量机(SVM)算法的建筑提取效果进行对比。在对比实验中,随机森林的决策树数目为200,每棵决策树随机选择

|
Download:
|
| 图 6 建筑提取结果对比 Fig. 6 Comparison of building extraction results | |
从提取结果可以看出,本文算法要优于随机森林和支持向量机这两种单分类器算法,随机森林算法在建筑区域内孤立点较多,支持向量机算法在植被和建筑混杂区域常常出现错分现象,而本文算法的实验结果中,植被与建筑边界更为清晰,分类结果具有更好的空间一致性。表 4给出实验结果的具体指标对比,本文算法的准确率和F1值均高于随机森林分类器和支持向量机分类器,体现了该算法的有效性和优越性。
|
|
表 4 AIRSAR八王子市建筑提取结果 Table 4 AIRSAR building extraction results of Hachiouji |
极化SAR图像能够为建筑提取提供丰富的特征,与单一类型特征相比,将多种类型特征组合起来有助于提高分类性能。本文利用随机森林将原始特征集进行特征筛选,保留对结果影响较大的特征,并将随机森林和支持向量机两种分类器的分类结果融合起来,得到了更理想的提取效果,AIRSAR极化数据证明了本文方法的有效性。随着SAR系统分辨率的提高,数据量也越来越大,因而接下来的研究方向之一是如何降低计算复杂度,另外,还需进一步研究如何在多分辨率、多波段的数据下保持算法的性能。
| [1] |
Lee J S, Pottier E.
Polarimetric radar imaging:from basics to applications[M]. Boca Raton: CRC press, 2009: 1-3.
|
| [2] |
Matsuoka M, Yamazaki F. Use of satellite SAR intensity imagery for detecting building areas damaged due to earthquakes[J]. Earthquake Spectra, 2004, 20(3):975–994.
DOI:10.1193/1.1774182 |
| [3] |
Henderson F M, Xia Z G. SAR applications in human settlement detection, population estimation and urban land use pattern analysis:a status report[J]. IEEE transactions on geoscience and remote sensing, 1997, 35(1):79–85.
DOI:10.1109/36.551936 |
| [4] |
Xiang D, Tang T, Ban Y, et al. Unsupervised polarimetric SAR urban area classification based on model-based decomposition with cross scattering[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 116(6):86–100.
|
| [5] |
Zhai W, Shen H, Huang C, et al. Fusion of polarimetric and texture information for urban building extraction from fully polarimetric SAR imagery[J]. Remote Sensing Letters, 2016, 7(1):31–40.
DOI:10.1080/2150704X.2015.1101179 |
| [6] |
车美琴, 阿里木, 赛买提, 等. 利用旋转不变特征提取全极化SAR影像人工地物[J]. 遥感学报, 2016, 20(2):303–314.
|
| [7] |
陈博, 王爽, 焦李成, 等. 利用0-1矩阵分解集成的极化SAR图像分类[J]. 电子与信息学报, 2015, 37(6):1495–1501.
DOI:10.11999/JEIT141059 |
| [8] |
Baghdadi N, Cresson R, El Hajj M, et al. Estimation of soil parameters over bare agriculture areas from C-band polarimetric SAR data using neural networks[J]. Hydrology and Earth System Sciences, 2012, 9(3):2897–2933.
DOI:10.5194/hessd-9-2897-2012 |
| [9] |
Salehi M, Sahebi M R, Maghsoudi Y. Improving the accuracy of urban land cover classification using Radarsat-2 PolSAR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(4):1394–1401.
DOI:10.1109/JSTARS.2013.2273074 |
| [10] |
Du P, Samat A, Waske B, et al. Random forest and rotation forest for fully polarized SAR image classification using polarimetric and spatial features[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 105(7):38–53.
|
| [11] |
孙勋, 黄平平, 涂尚坦, 等. 利用多特征融合和集成学习的极化SAR图像分类[J]. 雷达学报, 2016, 5(6):692–700.
|
| [12] |
Xia Z G, Henderson F M. Understanding the relationships between radar response patterns and the bio-and geophysical parameters of urban areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1):93–101.
DOI:10.1109/36.551938 |
| [13] |
赵凌君, 秦玉亮, 高贵, 等. 利用GLCM纹理分析的高分辨率SAR图像建筑区检测[J]. 遥感学报, 2009, 13(3):475–490.
|
| [14] |
Cloude S R, Pottier E. An entropy based classification scheme for land applications of polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1):68–78.
DOI:10.1109/36.551935 |
| [15] |
Yamaguchi Y, Moriyama T, Ishido M, et al. Four-component scattering model for polarimetric SAR image decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8):1699–1706.
DOI:10.1109/TGRS.2005.852084 |
| [16] |
Haralick R M, Shanmugam K, Dinstein I. Textural features for image classification[J]. Systems Man & Cybernetics IEEE Transactions on, 1973, smc-3(6):610–621.
|
| [17] |
Zhao L, Zhou X, Kuang G. Building detection from urban SAR image using building characteristics and contextual information[J]. EURASIP Journal on Advances in Signal Processing, 2013(1):1–16.
|
| [18] |
孙萍. 极化SAR图像建筑物提取方法研究[D]. 北京: 首都师范大学, 2013.
http://cdmd.cnki.com.cn/Article/CDMD-10028-1013291833.htm |
| [19] |
Dekker R J. Texture analysis and classification of ERS SAR images for map updating of urban areas in the Netherlands[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(9):1950–1958.
DOI:10.1109/TGRS.2003.814628 |
| [20] |
Genuer R, Poggi J M, Tuleau-Malot C. Variable selection using random forests[J]. Pattern Recognition Letters, 2010, 31(14):2225–2236.
DOI:10.1016/j.patrec.2010.03.014 |
| [21] |
陈刚, 王宏琦, 孙显. 基于核函数原型和自适应遗传算法的SVM模型选择方法[J]. 中国科学院大学学报, 2012, 29(1):62–69.
|
| [22] |
Díaz-Uriarte R, De Andres S A. Gene selection and classification of microarray data using random forest[J]. BMC bioinformatics, 2006, 7(1):1–13.
|
| [23] |
National Aeronautics and Space Administration (NASA). Airborne synthetic aperture radar (AIRSAR) system. Tokyo, Japan mission dataset[DB/OL].(2000-10-02)[2016-12-30].https://www.asf.alaska.edu/.
|
 2018, Vol. 35
2018, Vol. 35 


