2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar, SAR)是一种工作在微波波段的成像雷达,凭借其全天候、全天时、高分辨率、大面积的数据获取能力成为当前遥感观测的重要手段。但随着SAR图像的大量获取,并且由于其与光学成像系统的显著差异,传统的人工SAR图像车辆目标识别远远不能满足实际的应用需求,自动SAR图像车辆目标识别技术已经成为当今研究的热点[1]。目前国内外关于SAR图像目标识别已有大量文献。文献[2]直接采取模板匹配进行识别;文献[3]研究线性和非线性PCA(principle component analysis, 主成分分析)在SAR ATR中的应用;文献[4]首先利用NMF进行特征提取,然后选取SVM分类方法;文献[5-8]均是首先提取特征例如Gabor,PCA等,然后利用稀疏表示分类方法进行目标识别。文献[9-10]利用深度学习中的卷积神经网络进行目标识别;文献[11]采用多特征决策融合的技术来改善识别性能。
虽然上述文献都取得较好的识别性能,但均未考虑到实际情况中目标往往是非合作目标,很难获取一个目标的大量方位角SAR图像。所以针对稀疏方位角的训练样本的目标识别研究是一个重要的方向。文献[12]也考虑到非合作目标的情况,利用一种加权图像融合方法进行稀疏样本集扩充然后进行识别分类。而本文针对实际情况中的非合作目标识别问题,考虑到稀疏表示与PCA特征提取各自的优势[13],提出一种结合稀疏求解方法的改进PCA方法(improved PCA, IPCA),它首先利用稀疏求解方法为每个测试样本寻找最相关的k个训练样本,并得到这k个最相关的训练样本对测试样本的表示系数,然后基于传统的PCA方法和这些最相关的部分训练样本信息对测试样本进行分类。因此IPCA方法不仅具有传统PCA方法的效果,而且更有利于对测试样本的分类。
1 改进PCA方法原理 1.1 稀疏求解思想找k个最近邻样本稀疏描述的思想是用少量的样本来表示测试样本,其基本原理是假设有c类样本,其中Mi是第i类训练样本的个数,每个样本表示成一个列向量的形式,矩阵Ai表示第i类的所有训练样本,即
| ${\mathit{\boldsymbol{A}}_i} = [{\mathit{\boldsymbol{a}}_{i1}},{\mathit{\boldsymbol{a}}_{i2}}, \cdots ,{\mathit{\boldsymbol{a}}_{i{M_i}}}] \in {{\bf{R}}^{N \times {M_i}}},$ | (1) |
其中N表示向量的维数,aij(j=1, 2, …, Mi)表示第i类的第j个样本。当第i类的训练样本充足的时候,属于第i类的测试样本y能够较准确地由第i类的训练样本表示为
| $\mathit{\boldsymbol{y}} \approx {w_{i1}}{\mathit{\boldsymbol{a}}_{i1}} + \cdots + {w_{i{M_i}}}{\mathit{\boldsymbol{a}}_{i{M_i}}},$ | (2) |
系数wij(j=1, …, Mi)表示第i类的第j个样本对测试样本y的贡献。然而,事先不知道样本y所属的类别,所以矩阵Ai (i=1, …, c)进行合并形成一个字典矩阵A=[A1, A2, …, Ac]∈RN×M,其中
| $\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Aw}},$ | (3) |
其中w=[w11, …, w1M1, …, wi1, …, wiMi, …, wc1, …, wcMc]表示稀疏系数。根据式(2),属于类别i的测试样本的权重系数应该是
| $\mathit{\boldsymbol{w}} = \left[ {0, \cdots ,{\rm{ }}0, \cdots ,{\rm{ }}{w_{i1}}, \cdots {\rm{ }}{w_{i{M_i}}}, \cdots ,{\rm{ }}0, \cdots ,0} \right],$ | (4) |
也就是说,测试样本y能够被和它同类别的训练样本准确表示,而与它不同类的训练样本无关。考虑方程(3),给定y和A,解w与A∈RN×M密切相关。当N>M时,方程(3)是一个过定系统,w具有唯一解。但是大部分实际情况下N<M,方程(3)是欠定的,存在无数多个解。由式(4)知,最后的解w是稀疏的。所以方程(3)可以通过求解以下优化问题得到:
| $\mathit{\boldsymbol{w}}_0^* = {\rm{argmin}}{\left\| \mathit{\boldsymbol{w}} \right\|_0}\left( {{\rm{s}}.{\rm{t}}\;\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Aw}}} \right),$ | (5) |
式中‖·‖0表示L0范数,即一个向量中非零元的个数。式(5)在少量误差的情况下可以改写为
| $\mathit{\boldsymbol{w}}_{0}^{*}=\rm{argmin}{{\left\| \mathit{\boldsymbol{w}} \right\|}_{0}}~~(\rm{s}.\rm{t}~\ {{\left\| \mathit{\boldsymbol{y}}-\mathit{\boldsymbol{Aw}} \right\|}_{2}}\le \varepsilon ),$ | (6) |
其中ε表示误差为一个很小的正整数。然而式(6)的求解是一个NP问题,即多项式复杂程度的非确定性问题,不仅计算复杂度极高,而且解的可靠性也得不到保证。而研究[14]表明,式(6)的求解可以转化为L1优化问题即
| $\mathit{\boldsymbol{w}}_{0}^{*}=\rm{argmin}{{\left\| \mathit{\boldsymbol{w}} \right\|}_{1}}(\rm{s}.\rm{t}~\ {{\left\| \mathit{\boldsymbol{y}}-\mathit{\boldsymbol{Aw}} \right\|}_{2}}\le \varepsilon ),$ | (7) |
式(7)的优化问题可以通过迭代求解,这样每一个测试样本均要进行迭代计算,运算时间复杂度较高。为了提高SAR目标识别的速度,考虑直接利用所有训练样本去表示测试样本,保证表示误差最小化,即简化为如下优化问题进行快速求解:
| $\mathop {\min }\limits_\mathit{\boldsymbol{w}} {\left( {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Aw}}} \right)^2}.$ | (8) |
在实际情况中通常要求解向量w的范数较小,因此将式(9)的最小化作为我们的目标函数。
| $\begin{array}{l} L\left( \mathit{\boldsymbol{w}} \right) = {\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Aw}}} \right\|^2} + \lambda {\left\| \mathit{\boldsymbol{w}} \right\|^2} = \\ \quad \quad {\left( {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Aw}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Aw}}} \right)+\lambda {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}}, \end{array}$ | (9) |
式中λ为一小的正常数,利用拉格朗日方法:
| $\frac{{\partial L\left( \mathit{\boldsymbol{w}} \right)}}{{\partial \mathit{\boldsymbol{w}}}} = 0 \Rightarrow \mathit{\boldsymbol{w}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{y}},$ | (10) |
式中I表示单位矩阵。
假设A=[a1, a2, …, aM],利用公式(10)求出w,然后根据下式
| ${d_i} = {\left\| {\mathit{\boldsymbol{y}} - {w_i}{\mathit{\boldsymbol{a}}_i}} \right\|_2}$ | (11) |
计算第i个训练样本到测试样本的距离,取最小的k个距离的训练样本A′=[a1′, a2′, …, ak′]作为与测试样本最相关的样本。
利用式(10)重新利用最相关的k个训练样本构成新的训练样本矩阵A′对y进行描述,得到最相关的k个样本在测试样本描述中的权重w′=[w1′, w2′, …, wk′],其中越大的wi′对应的训练样本越与测试样本相关。
1.2 传统的主成分分析(PCA)首先对训练样本集A的每一列进行零均值化,然后计算A的协方差矩阵SX=AAT的特征值和相应的特征向量,实际上,当原始样本的每个向量的维数非常大时,协方差矩阵SX=AAT的维数将非常高,这样直接求取协方差矩阵的特征值和特征向量将付出很高的计算代价。事实上可以通过一种转化的方式先求矩阵ATA的前p个最大特征值和相对应的特征向量,再转化为求解SX=AAT的特征值和所对应的特征向量。假设γ, v分别表示ATA的特征值和相应的特征向量,则有
| $\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{v = \gamma v}}\mathit{\boldsymbol{.}}$ | (12) |
将式(12)两边同时左乘A得到
| $\mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{v = \gamma Av}},$ | (13) |
| $\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)\left( {\mathit{\boldsymbol{Av}}} \right) = \mathit{\boldsymbol{\gamma }}\left( {\mathit{\boldsymbol{Av}}} \right),$ | (14) |
从(14)式可以看出SX=AAT的特征值和特征向量分别为γ, Av。所以取矩阵ATA的前p个最大特征值对应的特征向量构成矩阵B,则SX=AAT的前p个最大值对应的特征向量构成的投影矩阵E=AB。E用于后续特征提取。
1.3 改进PCA特征提取分类利用式(15)和式(16)对最相关的训练样本和测试样本y进行特征抽取。
| ${\mathit{\boldsymbol{z}}_j} = w_j^{'}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{a}}_j^{'},j = 1,2, \cdots ,k,$ | (15) |
| $\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{y}}.$ | (16) |
式中,zj和z分别表示第j个最相关的训练样本aj′和测试样本y的特征抽取结果,即改进PCA的特征与传统PCA特征区别在于多了表示系数这一乘积项。最后根据下式将测试样本y分类到am′所属的类别。
| $m = \mathop {\arg \min }\limits_j \left\| {{\mathit{\boldsymbol{z}}_j} - \mathit{\boldsymbol{z}}} \right\|,j = 1,2, \cdots ,k.$ | (17) |
本文实验采用美国MSTAR数据库[15]中的3类SAR车辆静止目标BMP、BTR和T72,17°俯仰角的作为训练数据,15°俯仰角的作为测试数据,原始图像大小为128×128。实验数据由表 1所示,其中总共有698个训练样本,1 365个测试样本,通过对3类训练样本中每类的部分选取来考虑稀疏方位角训练样本集情况。本文所有实验均不对原始SAR目标图像进行任何预处理。
|
|
表 1 实验数据集 Table 1 Experimental dataset |
本文通过理想训练样本集实验和方位角稀疏训练样本集实验对改进的PCA方法(IPCA)和PCA方法进行识别性能对比,实验中2种方法的分类器均为最近邻分类器。图 1是本文改进PCA的SAR目标识别流程图。

|
Download:
|
| 图 1 改进PCA的SAR目标识别流程图 Fig. 1 Flowchart of IPCA SAR target recognition | |
首先在3类训练样本总共为698个的情况下进行实验,观察识别率随主成分数的影响,得到的实验结果如图 2所示。

|
Download:
|
| 图 2 识别率随主成分数的变化 Fig. 2 Variation in target recognition rate with principal component number | |
从图 2可以看出,随着主成分数的增加,IPCA与PCA的识别率都趋于稳定,说明提取一定维数特征的样本已经表达了足够的原始样本信息,并且IPCA的识别率始终比传统PCA的识别率要好5%左右,说明在理想训练样本集情况下,IPCA方法比传统PCA方法具有更好的识别性能。
2.2.2 稀疏方位角训练样本实验在前面实验结果的基础上,不妨选取主成分数p=50的条件下,对稀疏训练样本集进行实验。
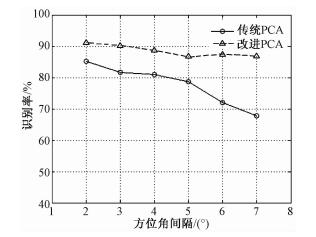
第1种情况:对每类训练样本进行等间隔方位角抽取,例如当方位角间隔为2°时,每类选取方位角为0°、2°、4°、…等训练样本,将IPCA与PCA分别用在等间隔方位角抽取训练样本集上的结果如图 3所示。从图 3可以看出,等间隔方位角抽取的间隔从2°递增到7°时,IPCA方法的识别率曲线一直处于PCA方法的识别率曲线之上,当每类训练样本从120左右降到30左右的时候,IPCA的识别率维持在90%左右,而PCA从85%降到大约70%,说明IPCA的识别精度随着方位角等间隔抽取度的增加下降不明显,相反传统PCA方法的识别精度随着方位角等间隔抽取度的增加而下降。可以看出IPCA比PCA在等间隔上的稀疏训练样本集上有更好的识别率和更高的鲁棒性。
|
Download:
|
| 图 3 等间隔稀疏训练集的实验结果 Fig. 3 Experimental results for equidistant interval sparse training set | |
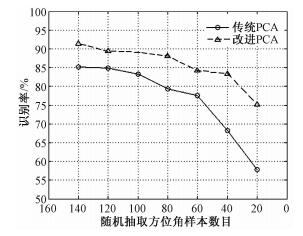
第2种情况:在每类训练样本中随机选取若干个方位角样本构成训练样本集进行实验。得到的实验结果如图 4所示。从图 4可以看出,随着每类训练样本的随机减少,IPCA始终比PCA有更好的识别率,并且每类随机剩下的训练样本越少,IPCA方法比PCA方法的识别性能优势越明显。例如,每类随机剩下140个训练样本时,IPCA比PCA的识别率高5%左右,当每类随机剩下20个训练样本时,IPCA比PCA的识别率高17%左右。所以IPCA对随机稀疏方位角训练样本集也有更好识别性能和更高的鲁棒性。
|
Download:
|
| 图 4 随机抽取的稀疏训练集的实验结果 Fig. 4 Experimental results for randomly selected sparse training set | |
综合以上可以得出,与传统的PCA方法相比,不管在方位角较全的训练集还是稀疏方位角训练样本集上,改进PCA方法都具有明显的优势,这是因为传统的PCA方法能够以最小的误差表示训练样本,但它不可以以最小的误差表示每一个测试样本。而IPCA首先利用训练样本为每一个测试样本提供不同的最优描述,然后结合表示系数信息进行特征提取,这样不仅具有传统PCA方法的效果,而且更有利于对测试样本的分类,并且它只需要计算测试样本与最相关的那些训练样本的距离来确定最终测试样本所属的类别,这样能减少训练样本中的噪声点对测试样本分类的影响,取得更高的识别率和更好的鲁棒性。
3 总结本文提出一种结合稀疏求解方法的改进PCA方法用于SAR图像车辆目标识别中,通过实验验证该IPCA方法可以有效地改善PCA方法的识别率,而且对稀疏训练样本具有更好的识别性能和鲁棒性,因此是一种有效的SAR图像非合作目标识别方法。本文没有对原始图像进行任何的预处理过程,研究预处理方法来提高目标的识别率是下一步工作的重点。
| [1] |
Maitre H. 合成孔径雷达图像处理[M]. 孙洪, 译. 北京: 电子工业出版社, 2005.
|
| [2] |
Novak L M, Owirka G J, Brower W S. Performance of 10-and 20-target MSE classifiers[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(4):1279–1289.
DOI:10.1109/7.892675 |
| [3] |
Mishra A K, Motaung T. Application of linearand nonlinear PCA to SAR ATR[C]//25th Int-ernational Conference Radioelektronika, RADI-OELEKTRONIKA 2015. Pardubice, Czech Republic:the IEEE Inc, 2015:349-354.
|
| [4] |
Cao Z, Min R, Pi Y, et al. The feasibility analysis of applying NMF in SAR target recognition[C]//IEEE International Conference on Digital Signal Processing, DSP 2015.Singapore:the IEEE Inc, 2015:721-725.
|
| [5] |
向卫力, 李晓辉, 周勇胜, 等. 一种鲁棒的多尺度稀疏表示SAR目标识别方法[J]. 中国科学院大学学报, 2016, 34(1):99–105.
|
| [6] |
刘中杰, 庄丽葵, 曹云峰, 等. 基于主元分析和稀疏表示的SAR图像目标识别[J]. 系统工程与电子技术, 2013, 35(2):282–286.
|
| [7] |
程建, 黎兰, 王海旭. 稀疏表示框架下的SAR目标识别[J]. 电子科技大学学报, 2014, 43(4):524–529.
|
| [8] |
Thiagarajan J J, Ramamurthy K N, Knee P, et al. Sparse representations for automatic target classification in SAR images[C]//4th International Symposium on Communications, Control, and Signal Processing, ISCCSP-2010. Limassol, Cyprus:IEEE Computer Society, 2010:1-4.
|
| [9] |
Morgan D A E. Deep convolutional neural networks for ATR from SAR imagery[C]//Algorithms for Synthetic Aperture Radar Imagery XXⅡ. Baltimore, MD, United states:SPIE, 2015:94750F.
|
| [10] |
Wang H, Chen S, Xu F, et al. Application of deep-learning algorithms to MSTAR data[C]//IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2015. Milan, Italy:the IEEE Inc, 2015:3743-3745.
|
| [11] |
Huan R H, Zhang P, Pan J. SAR ta-rget recognition using PCA, ICA and Gabor wavelet decision fusion[J]. Journal of Remote Sensing, 2012, 16(2):268–274.
|
| [12] |
丁军, 刘宏伟, 陈渤, 等. 姿态图像缺失情况下的SAR目标识别[J]. 西安电子科技大学学报, 2016, 43(4):5–9.
|
| [13] |
徐勇, 范自柱, 张大鹏.
基于稀疏算法的人脸识别[M]. 北京: 国防工业出版社, 2014.
|
| [14] |
Candès E J, Tao T. The power of convex relaxation:Nearoptimal matrix completion[J]. IEEE Transactions on Information Theory, 2010, 56(5):2053–2080.
DOI:10.1109/TIT.2010.2044061 |
| [15] |
Defense Advanced Research Project Agency (DARPA), Air Force Research Laboratory(AFRL).Moving and stationary target acquisition and recognition(MSTAR) public release dataset[DB/OL].(2015-09-21)[2016-10-20]. https://www.sdms.afrl.af.mil/datasets/mstar/.
|
 2018, Vol. 35
2018, Vol. 35 


