2. 微波成像技术国家级重点实验室, 北京 100190;
3. 中国科学院大学, 北京 100049
2. National Key Laboratory of Microwave Imaging Technology, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
合成孔径雷达(synthetic aperture radar, SAR)具有全天时、全天候的工作特点,随着成像分辨率的提高,合成孔径雷达图像在目标识别、情报获取等领域有着越来越广的应用前景。面对不断成长的SAR图像收集能力,如何快速、准确地对图像进行信息获取越来越受到重视,自动目标识别(automat-ic target recognition, ATR)就是在该需求下应运而生的技术。
最早期的SAR图像ATR技术基于模板匹配来实现[1-2],通过对每个目标类别建立模型,然后计算待预测目标和各模型的匹配度进行预测估计,该方法需要存储海量的目标模板,给识别系统的设计和算法效率的提高都造成了严重困难[3]。后来陆续有学者提出将Gabor滤波器[4]与支持向量机[5](su-pport vector machines, SVM)应用到SAR ATR技术中,但这些方法都依赖于前期类别特征的人工选取,也就难以避免地带来主观因素下的不标准性。卷积神经网络[6](convolutional neural networks, CNNs)能自动从数据集中提取目标类别特征[7],并且随着深度学习(deep learning)理论的发展[8],后续提出的深度卷积神经网络[9](deep convolutional neu-ral networks, DNNs)在目前最大的图像识别数据库ImageNet上取得了超出第2名正确率近10%的成绩[10]。2014年基于深度卷积神经网络的DeepFace、DeepID模型问世,直接将LFW(labeled faces in the wild)数据库上的人脸识别正确率提升至99.75%,几乎超越人类水平[11-12]。深度卷积神经网络模型在诸多图像识别领域已取得优于人工选取特征方法的成果[13]。除图像轮廓和颜色深浅等特征,SAR图像相比于普通光学图像还具有成像角度敏感性和大动态范围特性,这些特性给分类网络以额外的学习训练素材,本文拟将DNNs应用于SAR自动目标识别任务。
在深度学习任务中,复杂的模型需要数量庞大的训练样本的支持,否则容易出现过拟合(overfitting)和陷入局部最优解等现象。相比于ImageNet这种动则十几万数量级的光学图像数据库,SAR目标图像数据依旧过少。迁移学习[14]的加入很好地解决了训练样本不够所带来的上述问题,在图像识别[15]领域得到广泛应用。
本文将DNNs应用于SAR自动目标识别技术,用AdaGrad[16](adaptive subgradient methods)代替常用的SGD[17](stochastic gradient descent)作为权重优化函数,引入迁移学习概念,使用一种改进的网络结构对SAR目标图像进行识别。实验结果表明迁移学习可以改善网络参数的训练进程,基于DNNs的SAR图像识别比人工选取特征方法取得了更高的分类精确度。
1 深度卷积神经网络 1.1 网络拓扑结构深度卷积神经网络一开始为输入层,接受对应的输入图像数据。而后为隐藏层,负责特征的提取和组合,由简单特征到高度抽象完成图像的分类工作[13]。隐藏层通常由若干卷积层和池化层连接而成,最后由输出层输出判别结果。每一层都由不同权重值的神经元构成,连接着上下层网络,起到正向传输预测值和反向调整权重参数的作用。一个有效的学习网络应该对特定输入的图像在每一层产生正确的分类输出值。本文采取的DNNs具体网络拓扑结构和算法流程如图 1和表 1所示。
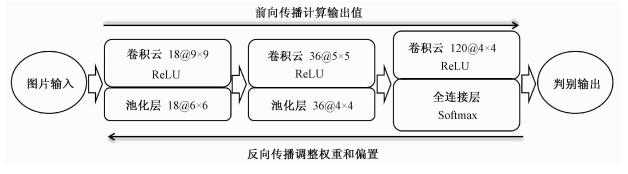
|
Download:
|
| 图 1 算法流程图 Fig. 1 Flowchart of algorithm | |
|
|
表 1 网络拓扑结构 Table 1 DNNs topology |
卷积神经网络通过卷积层完成局部感知野的作用,模拟视觉通路的特性。用不同卷积核对图片进行卷积以得到不同特征上的响应,完成多种局部特征的提取。图 2为卷积层示意图,以uil(m, n)表示第l层网络上卷积操作过后的第i个特征响应中间值矩阵,经激活函数后即得到l+1层的第i个输出矩阵xil+1(m, n),以Wjl(u, v)表示l层连接至l+1层的第j个卷积核。
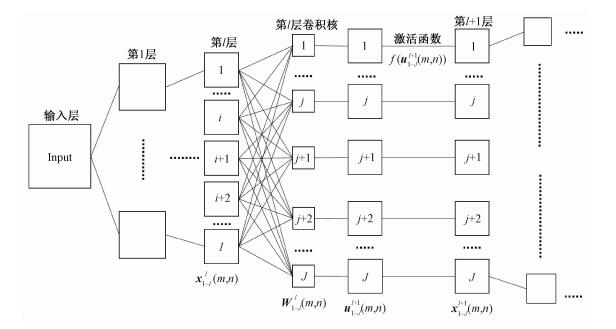
|
Download:
|
| 图 2 卷积层示意图 Fig. 2 Diagram of convolutional layer | |
首先由式(1)计算得到l层图像域在各个卷积核上二维卷积后的值:
| $\mathit{\boldsymbol{u}}_j^{l + 1}\left( {m,n} \right) = \sum\limits_{i = 1}^I {\sum\limits_{u,v = 1}^D {\mathit{\boldsymbol{W}}_j^l\left( {u,v} \right)\mathit{\boldsymbol{x}}_i^l\left( {m - u,{\rm{ }}n - v} \right) + \mathit{\boldsymbol{b}}_j^l} } ,$ | (1) |
其中bj为偏置值。然后将上述矩阵经过激活函数得到第l+1层的输出值
| $\mathit{\boldsymbol{x}}_j^{l + 1}\left( {m,n} \right) = f\left( {\mathit{\boldsymbol{u}}_j^l\left( {m,n} \right)} \right).$ | (2) |
假设输入层由I个大小为M1×N1的特征图组成,共有J个大小为F×F的卷积核,那么该卷积层的输出共包含J个大小为M2×N2的特征图。当选择步幅为S、填零尺寸为P时,输入输出特征图的大小关系为M2=(M1-F+2P)/S+1、N2=(N1-F+2P)/S+1。本文中参数选择S=1,填零尺寸为0。
为避免神经网络退化为最原始的感知机,每个卷积层都需要选择一个激活函数使得输入输出之间保持高度非线性的关系。在传统的DNNs中通常使用正切函数f(x)=tanh(x)或者Sigmod函数f(x)=1/(1+exp(-x))作为激活函数。但文献[18]表明使用ReLU(rectified linear units)函数能带来更好的网络稀疏性, 进而可以缓解过拟合问题的发生,此外还能改善深层网络Sigmod函数反向传播时梯度消失的问题。因此本文采用ReLU作为各层的激活函数,其形式如下
| $f\left( x \right) = {\rm{max}}\left( {0,x} \right).$ | (3) |
池化层能提升网络对输入图像平移旋转等抗畸变的能力,本文选择无重叠区域的最大池化(max-pooling)作为采样函数,其已被证实与平均池化(average-pooling)相比能更好地保留感知野之间的互信息特性[19],示意图如图 3所示。
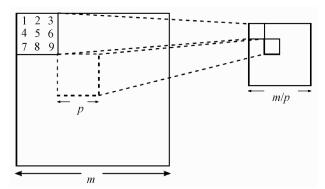
|
Download:
|
| 图 3 池化层max-pooling示意图 Fig. 3 Diagram of max-pooling layer | |
以s表示步长,p表示池化窗大小,最大池化的操作定义为
| $\mathit{\boldsymbol{x}}_i^{(l + 1)}\left( {m,n} \right) = \mathop {{\rm{max}}}\limits_{n,v = 0 \sim p - 1} \mathit{\boldsymbol{x}}_i^l\left( {m \times s + u,n \times s + v} \right).$ | (4) |
本文的池化层步长选择与池化窗大小相同,即无重叠模式的最大池化操作。
1.1.3 全连接层多分类网络的最后层需要输出待分类目标在各类别上的预测概率值,本文选择Softmax函数对网络输出各权重值进行计算得到最终多分类下的先验概率。假设最后隐藏层L的输出值是K维的矩阵,矩阵中每一个元素对应着待分类对象在各类别中的先验概率值pi=P(y=i|x),i=1,…,K,pi计算由式(5)给出:
| ${p_i} = \frac{{{\rm{exp}}(x_i^L)}}{{\sum {_{j = 1}^k{\rm{exp}}(x_j^L)} }},$ | (5) |
其中xiL为式(2)在L层所计算得到K维矩阵的第i个分量。
选择交叉熵损失函数衡量预测标签与实际标签差异的大小,假设共有n个待训练目标{(xi, yi), i=1, …, m},其中yi为各个对象的实际标签类型。在参数集为ω的分类网络下交叉熵损失函数定义为
| $L = - \frac{1}{n}\sum\limits_{i = 1}^n {\log P\left( {{y^i}|{x^i};\omega } \right)} .$ | (6) |
训练过程中通过最小化交叉熵损失函数提升分类正确率。通常无法直接计算得损失函数的全局最优解,但损失函数对网络中各参数的梯度∂L/∂ω却可以求得,因此可以通过迭代的数值优化方法降低损失函数值。如今广泛使用到的一种方法为梯度下降法,即通过ω←ω-ε(∂L/∂ω)迭代更新每个参数,反向传播梯度值使得网络参数逐步逼近最优解[20]。
1.2.1 初始化作为网络参数开始训练的第一步,权重初始化的常用方式有零值初始化和均匀分布初始化。本文选择文献[21]中所提到的Xavier方式进行初始化,该方式使得梯度值在网络各层保持大致相同的比例,用fanin、fanout分别表示与该层相连接输入输出层的神经元个数,则初始化的权重值均匀分布于
| $\left[ { - \sqrt {\frac{6}{{{\rm{fa}}{{\rm{n}}_{{\rm{in}}}} + {\rm{fa}}{{\rm{n}}_{{\rm{out}}}}}}} ,\sqrt {\frac{6}{{{\rm{fa}}{{\rm{n}}_{{\rm{in}}}} + {\rm{fa}}{{\rm{n}}_{{\rm{out}}}}}}} } \right].$ | (7) |
如式(8)所示,当选择常规的随机梯度下降法(stochastic gradient descent, SGD)作为优化函数时,各节点参数值的变化仅取决于所预设的全局学习率和误差函数的梯度值,其中学习率是SGD中唯一可控的超参数,需要不断试错调整它的值:
| ${\theta _{i + 1}} = {\theta _i} - \varepsilon \frac{{\partial E}}{{\partial \theta }}.$ | (8) |
SGD方法的一个缺点是,其更新方向完全依赖于当前批(batch)的训练对象,因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入动量(momentum),它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前批的梯度微调最终的更新方向。这样可以增加稳定性,从而学习地更快,并且还有一定的摆脱局部最优的能力。
| $\Delta {x_t} = \rho {x_{t - 1}} - \eta {g_t},$ | (9) |
其中,ρ表示要在多大程度上保留原来的更新方向,这个值在0~1之间,在训练开始时,由于梯度可能会很大,所以初始值一般选为0.5,当梯度不那么大时改为0.9。η是学习率,即当前批的梯度多大程度上影响最终更新方向。
上面提到的方法对于所有参数都使用同一个更新速率。但是同一个更新速率不一定适合所有参数。比如有的参数可能已经到了仅需要微调的阶段,但又有些参数由于对应样本少等原因,还需要较大幅度的调整。AdaGrad[16]就是针对这一问题提出的,自适应地为各个参数分配不同学习率的算法:
| ${g_{i + 1}} = {g_i} + {\left( {\frac{{\partial E}}{{\partial \theta }}} \right)^2},$ | (10) |
其中gi记录第i步迭代时候梯度平方的值。AdaGrad方法中参数迭代更新方式为
| ${\theta _{i + 1}} = {\theta _i} - \frac{\varepsilon }{{f + \sqrt {{g_{i + 1}}} }}\frac{{\partial E}}{{\partial \theta }},$ | (11) |
其中f为一个常量值,意在防止参数训练开始阶段学习率出现无穷大的情况。
1.2.3 基于迁移学习的SAR自动目标识别为了训练过后能在目标数据集上取得良好的分类效果,传统的机器学习方法要求训练集和测试集具有相同的特征空间和数据分布,而某些情况下数据集的搜集并非易事,比如特定语料的标注和本文中的SAR图像识别等[22]。迁移学习概念的提出很好地解决了训练样本缺失所导致的局部最优解和过拟合等问题。
深度卷积神经网络对目标特征的学习是一个从局部细节到高度表征的过程,虽然2个相似的数据集从宏观上来说不尽相同,但包括图像的边界特性和色彩斑点在内的某些局部特征二者是一样的[14],即在这2个数据集上得到的分类网络前几层的参数具有高度相似性,基于这个性质提出同构迁移学习、异构迁移学习和负迁移学习[22]的概念。本文将同构迁移学习加入到SAR图像目标识别任务,首先按上述学习过程获得目标分类网络在某一相似数据集上的预训练结果,由于其和目标数据集共享某些局部特征,预训练结果的前几层网络参数已经接近最终值。然后根据2个数据集的相似程度将预训练结果的最后若干层网络重新初始化,并用它在目标数据集上进行参数微调(fine-tuning)操作得到最终值。得益于在相似样本上的学习过程,预训练结果已经能很好地识别出样本细节特征,在此基础上的微调一方面能改善由不同批训练样本导致的参数优化方向不确定性,另一方面能避免训练样本数过少带来的过拟合问题。
2 实验结果为了验证各种SAR图像分类算法的有效性,美国国防研究规划局(DARPA)和空军研究实验室(AFRL)联合研发了运动和静止目标获取与识别(moving and stationary target acquisition and recognition, MSTAR)数据库,目前被广泛应用于SAR自动目标识别中。本文选择MSTAR数据库对网络进行分类训练和测试。
2.1 基于DNNs的SAR自动目标识别实验结果实验数据选自MSTAR数据集中图像大小为128×128的10类目标观测数据,表 2给出训练集和验证集的组成,并在图 4给出每种目标类别实际的光学照片和MSTAR数据库中成像效果对比。
|
|
表 2 实验数据构成 Table 2 Experimental data composition |

|
Download:
|
| 图 4 各目标型号对比示意图 Fig. 4 Diagram of target models | |
将上述数据集作为输入,学习速率ε=0.01,正则项f=0.1,批大小(BatchSize)选择为49,在每个时期(epoch)过后都重新随机排列数据集,将训练集共2 747幅数据作为输入对本文第二部分的网络进行训练。实验平台为Ubuntu 16.04+TensorFlow,网络在验证集上识别准确率和损失函数值随着迭代次数的变化如图 5所示。可以看到随着迭代步数的更新,整体识别正确率最终达到98.73%,并且经过前期的参数学习,在4 200步(75 epochs)之后数据集的识别正确率和损失函数值已无较大波动。为了更好地研究网络对各验证集的分类正确率,表 3给出在该DNNs网络每个子类别SAR图像上的最终识别结果。
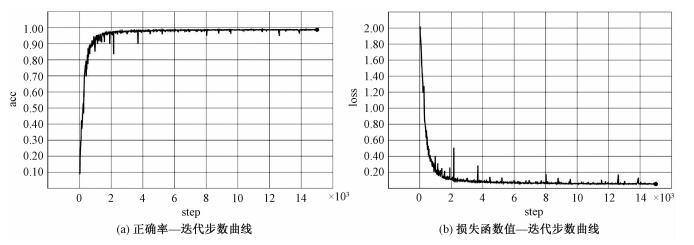
|
Download:
|
| 图 5 零基础训练下10类目标的分类情况 Fig. 5 Recognition performance of the 10 classes of targets using the method of training from scratch | |
|
|
表 3 各类目标的分类正确率结果 Table 3 Classification accuracies of the 10 classes of targets |
为了验证迁移学习在雷达图像领域的适用性,本文先在MSTAR的5类数据集上进行分类训练并获得分类模型,然后在这个模型的基础上对另外5类和10类目标图像进行分类训练,并与这2个数据集在非迁移学习模式下的学习率变化曲线进行比对,以验证训练集分别在有无重叠情况下迁移学习所带来的影响。其中用于训练原始模型的5类数据集包含的目标类别有BRDM-2、BTR-60、D7、T-72和ZSU-234。用于验证迁移学习效果的另外5类数据集包含目标2S1、BMP-2、BTR-70、T-63、ZIL-131,另外10类数据集包含目标BRDM-2、BTR-60、D7、T-72、ZSU-234、BMP-2、BTR-70、T-62、2S1和ZIL-234。图 6给出在零基础训练和迁移学习模式下的分类正确率和损失函数曲线对比。
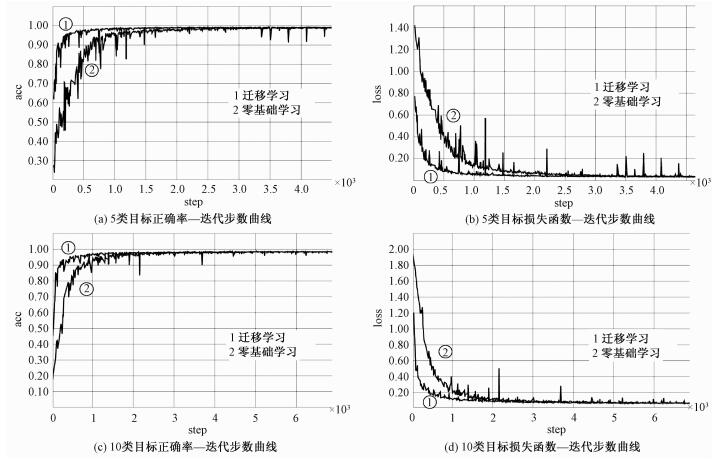
|
Download:
|
| 图 6 迁移学习和零基础学习实验结果对比 Fig. 6 Comparison of recognition performance between the method of transfer learning and the method of training from scratch | |
从图 6可以看到,对5类数据集进行分类时,零基础学习的分类正确率初始值为27.6%,同期的迁移学习方法下初始值高达61.8%。经过约1 600步(57 epochs)迭代后迁移学习模式下的网络分类正确率已达峰值99.26%,约3 000步(106 epochs)之后二者均达到最高值。
而对于在原始5类数据集上添加另外5类对象的迁移学习来说,正确率初始值分别为17.7%和45.1%。经过约3 000步(53 epochs)后迁移学习模式下的分类正确率达到99.01%的峰值,略高于零基础学习模式下于4 200步(75 epochs)取得的98.73%。迁移学习模式在以上2种训练集的迭代曲线都更加平滑,并且模型训练速度更快。
深度卷积神经网络通过梯度下降法ω←ω-ε(∂L/∂ω)迭代更新每个参数,使得网络参数逐步逼近最优解。由于梯度值是基于目前批的训练目标计算得到,所以每一次参数的优化方向只是朝局部最优解进行,而局部最优解有时和全局最优解相差甚远,此时便产生了图 6的毛刺现象。通过对比可以看到,迁移学习的迭代曲线相比于零基础学习更加平滑,在训练目标数目较少(5类)的情况下对比会更加明显,也就说明迁移学习模式下的每一次迭代过程更加趋向于全局最优解、避免了陷入局部最优问题的发生,并且明显加快了网络参数的训练进程。
目前广泛采取的另外4种SAR自动目标识别技术有支持向量机[23]、条件高斯模型[24]、修正的极化匹配分类器[25]和单基因尺度空间法[26]。为了衡量本文方法的有效性,表 4给出迁移学习模式下的DNNs识别法和以上4种方法的平均分类正确率对比。
|
|
表 4 各方法下的分类正确率对比 Table 4 Comparison of recognition performance among the classification methods |
由表 4可见在SAR图像目标识别任务中,迁移学习下的DNNs相比于其他识别模型能取得更高的分类正确率。目前很多将DNNs应用于SAR自动目标识别的相关研究已得到展开,文献[27]用较浅的卷积神经网络模型对SAR图像进行识别,其模型由3个卷积层和全连接层构成,在MSTAR数据集10类目标识别中取得93.99%的正确率。文献[28]将主成分分析技术和卷积神经网络相结合,在相同的数据集下识别正确率达到96.97%。文献[29]使用基于深度卷积神经网络的快速RCNN模型对SAR目标进行识别,在MSTAR数据集的8类样本识别中取得99.0%的识别率;但其网络模型共由5个卷积层、3个池化层和3个全连接层组成,与本文相比,其更深的网络模型在提升正确率的同时有可能会加长模型的训练时间、降低其效率。
3 结论本文使用一种改进的深度卷积神经网络对SAR图像目标进行识别,无需人工特征预选取操作即可让网络自动学习类别特征。为了避免分类网络陷入局部最优解和加快模型训练速度,本文还将迁移学习概念加入到SAR自动目标识别技术中,并在最后使用MSTAR数据集进行实验验证。结果表明基于深度卷积神经网络的SAR目标识别在迁移学习模式下取得高达99.01%的识别率,相比于零基础学习模式缩短了1/3(10分类)至近一半(5分类)的训练时间,该方法在SAR自动目标识别领域具有良好的应用前景。后续工作准备在相同条件下对2种学习模式进行多次实验记录,训练所需时间,以定量评估二者之间的效率差异。
| [1] |
O'Sullivan J A, Devore M D, Kedia V, et al. SAR ATR performance using a conditionally Gaussian model[J]. IEEE Transactions on Aerospace & Electronic Systems, 2001, 37(1):91–108.
|
| [2] |
Srinivas U, Monga V, Raj R G. SAR automatic target recognition using discriminative graphical models[J]. IEEE Transactions on Aerospace & Electronic Systems, 2014, 50(1):591–606.
|
| [3] |
张锐, 洪峻, 明峰. 基于目标CSAR回波模型的SAR自动目标识别算法[J]. 电子与信息学报, 2011, 33(1):27–32.
|
| [4] |
向卫力, 李晓辉, 周勇胜, 等. 一种鲁棒的多尺度稀疏表示SAR目标识别方法[J]. 中国科学院大学学报, 2017, 34(1):99–105.
|
| [5] |
Zhao Q, Principe J C. Support vector machines for SAR automatic target recognition[J]. IEEE Transactions on Aerospace & Electronic Systems, 2001, 37(2):643–654.
|
| [6] |
Lecun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11):2278–2324.
DOI:10.1109/5.726791 |
| [7] |
Chen S, Wang H, Xu F, et al. Target classification using the deep convolutional networks for SAR images[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(8):4806–4817.
|
| [8] |
Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786):504–507.
DOI:10.1126/science.1127647 |
| [9] |
Bengio S, Deng L, Larochelle H, et al. Special issue on learning deep architectures[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(1):207–207.
DOI:10.1109/TPAMI.2012.8 |
| [10] |
Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems. Curran Associates Inc, 2012:1097-1105.
|
| [11] |
Taigman Y, Yang M, Ranzato M, et al. DeepFace:closing the gap to human-level performance in face verification[C]//IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2014:1701-1708.
|
| [12] |
Sun Y, Wang X, Tang X. Deep learning face representation from predicting 10000 classes[C]//IEEE Conference on Computer Vision and Pattern Recognition. IEEE Computer Society, 2014:1891-1898.
|
| [13] |
Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553):436–444.
DOI:10.1038/nature14539 |
| [14] |
Yosinski J, Clune J, Bengio Y, et al. How transferable are features in deep neural networks?[J]. Eprint Arxiv, 2014, 27:3320–3328.
|
| [15] |
Li W, Duan L, Xu D, et al. Learning with augmented features for supervised and semi-supervised heterogeneous domain adaptation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 36(6):1134–1148.
|
| [16] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 2011, 12(7):2121–2159.
|
| [17] |
Bottou L, Bousquet O. The tradeoffs of large scale learning[C]//International Conference on Neural Information Processing Systems. Curran Associates Inc, 2007:161-168.
|
| [18] |
Grósz T, Gosztolya G, Tóth L. A sequence training method for deep rectifier neural networks[J]. Speech Recognition, 2014, 8773:81–88.
|
| [19] |
Scherer D, Müller A, Behnke S. Evaluation of pooling operations in convolutional architectures for object recognition[C]//Artificial Neural Networks ICANN 2010, International Conference, Thessaloniki, Greece:Proceedings. DBLP, 2010:92-101.
|
| [20] |
江璐, 赵彤, 吴敏. 基于深度卷积神经网络的指纹纹型分类算法[J]. 中国科学院大学学报, 2016, 33(6):808–814.
|
| [21] |
Bengio Y. Practical recommendations for gradient-based training of deep architectures[M]//Neural Networks:Tricks of the Trade. Springer Berlin Heidelberg, 2012:133-144.
|
| [22] |
Pan S J, Yang Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge & Data Engineering, 2009, 22(10):1345–1359.
|
| [23] |
Zhao Q, Principe J C. Support vector machines for SAR automatic target recognition[J]. IEEE Transactions on Aerospace & Electronic Systems, 2001, 37(2):643–654.
|
| [24] |
O'Sullivan J A, Devore M D, Kedia V, et al. SAR ATR performance using a conditionally Gaussian model[J]. IEEE Transactions on Aerospace & Electronic Systems, 2001, 37(1):91–108.
|
| [25] |
Park J I, Kim K T. Modified polar mapping classifier for SAR automatic target recognition[J]. IEEE Transactions on Aerospace & Electronic Systems Aes, 2014, 50(2):1092–1107.
|
| [26] |
Dong G, Kuang G. Classification on the monogenic scale space:application to target recognition in SAR image[J]. IEEE Transactions on Image Processing, 2015, 24(8):2527–2539.
DOI:10.1109/TIP.2015.2421440 |
| [27] |
张慧, 肖蒙, 崔宗勇. 基于卷积神经网络的SAR目标多维度特征提取[J]. 机械制造与自动化, 2017(1):111–115.
|
| [28] |
史鹤欢, 许悦雷, 马时平, 等. PCA预训练的卷积神经网络目标识别算法[J]. 西安电子科技大学学报(自然科学版), 2016, 43(3):161–166.
|
| [29] |
李君宝, 杨文慧, 许剑清, 等. 基于深度卷积网络的SAR图像目标检测识别[J]. 导航定位与授时, 2017, 4(1):60–66.
|
 2018, Vol. 35
2018, Vol. 35 


