2. 中国科学院南京地理与湖泊研究所, 南京 210008;
3. 中国科学院大学, 北京 100049;
4. 犹他大学地理系, 美国 盐湖城 84112-9155
2. Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210008, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Department of Geography, University of Utah, Salt Lake City 84112-9155, USA
公共服务设施是为市民提供公共服务产品的各种社会性的具有服务功能的基础设施[1],随着新型城镇化的推进,其社会需求日益增长,但由于数量缺乏、质量落后等因素,供求矛盾日益突出。公共服务设施的“不平衡地理”问题引起了学者的注意。哈维提出“空间区隔”的概念,教育资源的空间差异导致的受教育机会和权利不同会对社会流动形成严格限制,使教育不平等问题表现出层次更深、内容更广的特点,进而引发社会不平等的代际传递[2]。基础教育设施关系到社会稳定大局,成为公共服务设施研究的重点议题[3]。根据城市空间生产理论,城市化的过程包含资本的三级循环,而对教育等公共服务设施的投资是第三级循环的重要内容,需要通过国家机构组织规划,才能找到改善劳动力质量的渠道[4]。合理规划教育设施有利于发挥其知识溢出效应[5],推动新型城镇化的发展。
目前,地理学界已对基础教育设施进行了相关研究。从研究内容上看,主要有从距离范围的角度出发,分析教育可达性的空间公平性、各区域数量均衡性以及时间可达性差异[6];也有关注建筑层面的微观可达性[7]和心理距离的承受度[8];从规划的角度出发,分析建设的成本和效益从而进行布局调整[9],结合人口特征进行各类设施选址修建的决策[10]。从研究方法和成果上看,Taleai等[11]基于地理分析方法,引入一个基于多标准分析的综合空间公平性评估框架,发现研究区域的部分地区在合理的距离内仍无法充分利用教育等公共服务;谢婷婷等[12]借助公共服务设施区位理论和GIS网络分析技术,通过构建空间分布公平指数模型,发现兰州市城市教育设施空间分布存在显著的差异特征;杜俊秀等[13]通过建立中小学分布水平指标体系的方法,对东营市辖区中小学布局水平进行评价并发现东营区整体中小学布局水平存在不均衡现象、城乡差异明显的问题;郭全[14]利用比例模型和Huff模型分析方法分析居民点、学生和教育服务的关系,发现兰州市城关区基础教育资源空间分配不均衡等问题;Teixeira和Antunes[15]利用离散层级选址模型分析公共设施规划中的问题,并在学校网络的规划中证明模型的有效性;Dadashpoor等[16]利用空间不公平性测量综合模型测算城市地区所有设施的空间不均衡水平,发现大多数居民都有过由于空间不均衡问题所带来的不便体验。上述研究主要从静态的视角研究基础教育设施的空间格局。在动态研究方面,主要有卢晓旭等[17]采用集聚维数、最短时间法测度南京高级中学集聚性与可达性的时空变化,得出“十一五”期间南京市普通高中总体规模在扩大,但规模差异在缩小和趋于均衡等结论,赵晨旭等[18]利用趋势面分析等方法对武陵山区乡村学校空间格局演变特征及发展水平进行实证分析,得出有关乡村学校规模变化特征与不同类型区乡村学校服务范围变化规律等结论。但以上研究皆缺乏对城市各类基础教育设施的全面把握,偏重学校个体数量的增减,对教育联系和教学质量的关注不够。教育设施规划的完善提升必须关注其动态变化规律、加强教育合作和发挥教学功能的实际效果。南京市教育业的“十三五”规划提出,到2020年率先实现较高水平的教育现代化,达到这一目标需要对基础教育设施的空间规划有科学的认识。
本文采用多种GIS空间分析和社会网络分析方法,结合2006—2015年南京幼儿园、小学、初高级中学的空间和属性数据,对南京市基础教育设施空间结构演化特征进行研究,以期为后续教育设施优化布局管理提供参考并为公共服务设施研究提供新思路。
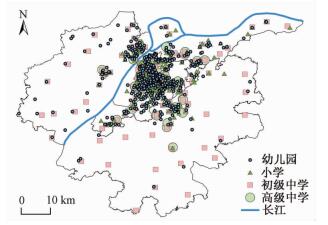
1 研究方法和数据 1.1 研究区概况根据南京市2015年行政区划,选取鼓楼、玄武、秦淮、建邺、雨花台、江宁、浦口、栖霞共8个市辖区作为研究范围,总面积3 262.11 km2(图 1)。依据南京市统计局的标准,将前4区统称为城区,其他则为郊区。由于六合、溧水和高淳等3区过于偏远且教育管理制度与其他8区存在极大差别,故不纳入研究范围。
|
Download:
|
| 资料来源:作者依据南京市教育局网站地图改绘。 图 1 研究区及2015年基础教育设施分布图 Fig. 1 Study area and distribution of basic educational facilities in 2015 | |
作为“六朝古都”和首批国家历史文化名城,自古以来南京的基础教育就在全国地位突出。明清两代学塾兴盛,秦淮区的江南贡院一度为全国最大的科举考场。民国时期,学制改革兴起,南京出现了现代意义的中小学校。新中国成立后,特别是进入21世纪以来,基础教育设施快速发展。2000年,研究区有幼儿园467所,小学735所,初中132所,高中66所,其中城区分别占比60%、29%、27%和48%;到2005年,共计有幼儿园384所,小学287所,初中104所,高中62所,城区占比分别变为58%、39%、50%和58%,这一空间结构为基础教育设施进一步的时空演化提供了基础。
1.2 数据来源根据2015年1月26日南京市政府发布的最新版《南京市公共设施配套规划标准》(简称“新规划标准”),基础教育设施包括幼儿园、小学、初级中学和高级中学的场地和建筑。基于2015年的南京市及各区教育局网站的教育地图和学校列表获取基础教育设施的名录数据。2006年数据是综合《南京市中小学校园用地规划(2006—2020)》和《南京市全域地图(2006年版)》以及《南京市统计年鉴(2007)》等资料取得。通过百度地图收集地理位置数据,建立南京市基础教育设施空间数据库。教育联系和升学成绩数据来自市教育局和各学校官方网站。图表均为作者按照相关数据自主整理绘制。
由于数据的可获得性,以名校设立或创办分校的时空数据来表征教育合作联系,探讨优质教育资源空间扩散过程。市“十三五”教育规划将名校设立分校作为加强教育联系合作的主要途径。因此仅以名校分校的设置作为教育设施联系的指标虽然有一定局限性,但其在教育合作联系中具有相当程度的代表性,能够反映核心的问题和趋势。
1.3 研究方法 1.3.1 平均最邻近距离法平均最邻近距离可判定同类基础教育设施点的平均距离,并根据测量平均最邻近距离值di与期望平均最邻近距离值de的比率R表征基础教育设施的空间集聚性。该比率R可表示为
| $R = \frac{{{d_{\rm{i}}}}}{{{d_{\rm{e}}}}} = \frac{{{d_{\rm{i}}}}}{{0.5\sqrt {N/A} }},$ | (1) |
式中:N为基础教育设施的数量,A为研究区面积。当R<1时,表示基础教育设施是集聚分布,存在一组或一组以上的点集聚群,每个设施点与其最近邻的各设施点距离很小,而另外的很大区域则没有设施点;当R>1时,为均匀分布,表示每个设施点与其他设施点最邻近点距离大致相等;当R=1时,为随机分布,表示其中有些设施点较为集中,而有些设施点则较分散。其标准差Z可表示为
| $Z = \frac{{({d_{\rm{i}}} - {d_{\rm{e}}})\sqrt {{N^2}/A} }}{{0.26136}}.$ | (2) |
式中:在集聚的情况下,Z>0,此时Z得分越高,显著性p值越小;Z的临界值2.58、1.96和1.65分别对应p值的0.01、0.05和0.1;p值越小,则集聚性越显著[19]。
1.3.2 核密度估计法通过使用核密度估计法考察规则区域中点密度的空间变化和研究点的分布特征。以每个待计算格网点为中心,在圆形半径内进行搜寻,然后计算每个格网的密度值,其中靠近搜索圆形区域中心的点会被赋予较大权重,随着其与格网中心距离的增加则权重降低[20],计算和制图用ArcGIS实现。核密度函数值越大,说明该类基础教育设施布局越密集,反之则越稀疏。
1.3.3 社会网络分析法为反映教育联系格局变动情况,收集了截至2015年10月的南京市所有中小学名校和幼儿园名园的分校设置数据,包括名称和设置时间。以设置分校作为教育联系的体现,绘制南京市基础教育网络图。将该网络定义为一个矩阵,根据当年两校之间是否存在联系进行0-1赋值,得到二值化矩阵,形成节点之间联系的1-mode网络,使用社会网络分析软件Ucinet对数据进行分析。根据社会网络测度区域内外联系的E-I指数构建边界效应的量化指标[21],以边界效应来考察不同年份名校分校跨区域设置的变化。表达式为
| $\gamma = \frac{{D{S_{{\rm{subarea}}}} - D{S_{{\rm{area}}}}}}{{D{S_{{\rm{subarea}}}}}},$ | (3) |
式中:γ为边界效应;DSsubarea为区内教育联系密度;DSarea为市内教育联系密度,DS根据平均点度中心度[22]来计算,具体操作通过Ucinet软件来实现。以边界效应γ来考察优质基础教育设施跨区域设置的变化,γ值越大,表明边界起到的阻碍作用大,更倾向在区内设置分校而非跨区设置,反之亦然。
节点度分布是描述网络几何特征的核心统计参数,将位序规模法则的幂律分布函数引入网络分析,表达式为
| $p\left( k \right) = c{k^{ - Q}}.$ | (4) |
式中:c为常数,Q称为幂指数,k表示节点度数,p(k)表示度数为k的节点数占总节点数的比例。Q在一定程度上可以度量网络节点的异质性,值越大则异质性越弱[23]。
考虑到少数节点度数明显偏大或存在多中心的情形,上述模型容易受到个别特殊点的影响,对网络结构总体特征的拟合程度有所欠缺。因此,从逆向排序的节点度数累积规模与节点数目之间的关系出发,建立反映教育联系网络规模结构特征的对数复合模型
| ${\rm{ln}}{M_n} = \eta \cdot {\beta ^{{\rm{ln}}n}},$ | (5) |
式中:Mn为教育网络体系内逆向排序的前n位节点的度数累积规模,η与β为待估参数。η为常数,β值反映的是节点度数逆序累积规模增长的速度,此处将其称为复合指数。一般而言,β值越小,网络体系的首位度越低,网络结构越完善,网络异质性越小。
2 数量结构的演化 2.1 空间集聚性演化基于平均最邻近距离,采用ArcGIS分析不同类型基础教育设施的空间集聚性及演化特征。如表 1,根据p值和R值特征可见,按照从高中到幼儿园的顺序集聚性依次增强。空间分析结果与各类型基础教育设施的自身特征基本吻合:高中是级别最高的基础教育设施,校园面积较大,采用统一考试招生,汇聚来自全市各地的学生,由于其规模大,故区域内设立的高中相对分散;小学和幼儿园面积较小,秉持的是“就近入学”的原则,在空间布局中较为集聚;初中和小学一样实行以空间近域范围为基础的学区制度,但初中单个教育设施服务覆盖面更广,常为若干个小学学区之和,故分布集聚性低于小学。依据“新规划标准”,各类基础教育设施在服务半径上存在明显差异:高中的服务范围涵盖全市所有经考试录取的学生,单个高中的规划服务人口为10万人;初中服务半径为1 000 m,服务人口为3万人;小学服务半径为500~1 000 m,服务人口为1.5~1.8万人;幼儿园服务半径为300 m,服务人口为1万人。因此在人口密集区域,小学和幼儿园的空间集聚性要明显高于高中。
|
|
表 1 各类基础教育设施空间集聚性演化 Table 1 Spatial aggregation of various basic educational facilities |
平均邻近距离按高中、小学、幼儿园的顺序依次递减,体现了不同类型基础教育设施对可达性要求的差异。2006—2015年,高中和初中的集聚性下降,而小学和幼儿园的集聚性上升,可能的原因是前两者更注重区域总体均衡,而后两者更关注局部空间便利。除初中外基础教育设施的平均邻近距离均为下降,初中的平均邻近距离最长且呈上升态势,原因可能是其他基础教育设施的扩张主要为内部空缺填充或从密集区边缘外延,而初中则更倾向于在偏远地区孤岛式的布局。
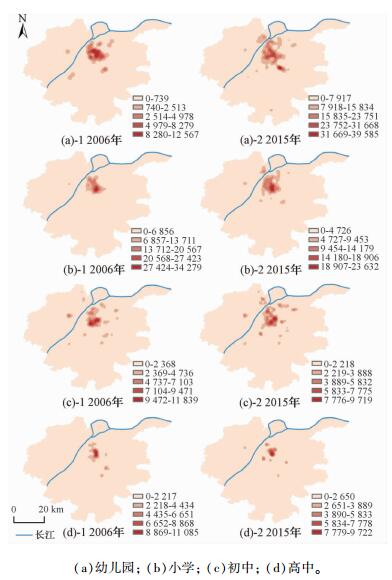
2.2 空间热点演化采用核密度估计法分析南京基础教育设施空间热点的演化特征。从宏观上看,幼儿园在2006年的分布呈现出内城区多核结构、外部相对稀疏的特征(图 2(a))。到2015年,峰值区急剧扩大,雨花台区和浦口桥北地区的核密度值大幅提高,下关地区、迈皋桥地区和仙林地区的核密度值也有所提升。江宁区形成了新的高值极核,作为幼儿园大规模集聚地的特征日益凸显。
|
Download:
|
| 图 2 2006和2015年基础教育设施核密度 Fig. 2 Kernel density analysis of basic educational facilities in 2006 and 2015 | |
小学的分布呈现以中心城区为核心,向周边区域扩展的模式(图 2(b))。就具体区域而言,在中心城区内部,小学峰值区主要呈向西移动的态势。随时间推移,小学由中心城区进一步向郊区扩张,次级集聚的特征明显,呈现从中心城区向郊区等级扩散的模式。2006年,小学主要集中在城墙范围以内的老城区。随后峰值区向周围蔓延扩展,到2015年,形成涵盖中心城区主要范围的集聚峰区。此外,郊区的核密度也有所提升,特别是浦口区和江宁区的核密度值也有较大幅度的提高,峰值区不断扩大,形成新的集聚热点。这些演化特征呼应了南京市“跨江发展”和“多中心发展”的战略[24]。
初中的空间热点演化特征与小学存在一定差异(图 2(c))。在中心城区内部,小学主要呈单极核结构,而初中呈现出双极核结构。随时间推移,初中进一步向外部扩张,次级集聚的特征明显,尤其是在鼓楼区和下关区合并以后,新鼓楼区西北部核密度值也有较大幅度的提高,峰值区不断扩大,有逐渐形成第三极核的趋势。相对于小学而言,初中向城东地带扩散的倾向更为明显,如仙林地区、迈皋桥地区等。
高中的空间扩散力度远远低于小学和初中(图 2(d)),峰值增加范围相当有限,主要向主城区西北和西南方向扩散,跨江散相对较少。
3 教育联系与质量的时空演化基础教育设施的演化不仅是空间数量的变化,也是教育联系与质量差异的改变。基础教育空间联系合作的发展在一定程度上推动教育质量的演变。
基础设施空间联系网络的改善为促进知识扩散和区域创新发展提供了条件[25],因此如何健全优质教育的合作网络体系应成为制定城市教育和规划政策的重要方向。名校在其本部服务范围外的区域设立分校是建立和加强基础教育设施间合作联系的主要模式[26],“以强带弱”有利于扩大优质教育资源共享范围,改善基础教育设施发展的空间不均衡性。
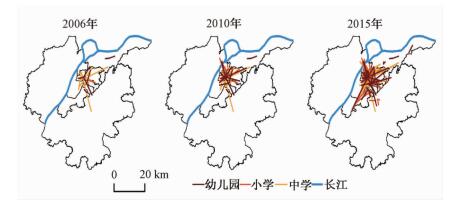
根据名校分校设置时间顺序,分阶段观察教育联系网络的空间演化特征(图 3)。2001年,鼓楼区力学小学将同区银城小学设为直属分校,开启名校资源空间扩散的序幕。到2006年为止,幼儿园和小学分校设置较少,以中学为主,向远郊扩散较少,无跨江扩散。
|
Download:
|
| 图 3 基础教育联系网络的空间演化 Fig. 3 Spatial evolution of basic educational connection network | |
2007年,玄武区北京东路小学和鼓楼区琅琊路小学分别在浦口区设立分校,突破了长江阻隔,江北区域开始分享优质教育资源。2010年,鼓楼区加强区内教育资源整合力度,成立力学小学教育集团,将本区3所小学设为力学小学分校。在2007—2010年间,名校资源的扩散方向更多倾向于北部地区,而向南方扩散相对较少。
2013年原鼓楼区与下关区、原秦淮区与白下区合并。新鼓楼区积极推进两地教育资源整合,组建7个教育集团,促进名优学校空间扩散,如原下关区复兴小学在两区合并后成为原鼓楼区力学小学的直属分校。新秦淮区成立扩大化教育共同体,对部分力量相对薄弱的小学实行名校托管,如原秦淮区双塘小学被原白下区游府西街小学托管,派其副校长任校长。2011—2015年间,名校教育资源在北方的扩散进一步加强,同时向南部地区特别是雨花台区的扩散急剧增加,如板桥新城的房地产企业积极与名校合作在当地建设分校。栖霞区和江宁区出现区内小学名校扩散的现象,反映边缘郊区自身教育发展水平有所提升。
通过幂律函数模型和对数复合模型对整体网络结构变动的复杂性(表 2)进行分析,方程的F统计值与变量的t统计值均通过了5%的显著性检验。根据幂律函数模型的结果,2006—2009年Q值总体呈现波动下降的趋势,网络异质性明显增强。从2010年开始,Q值一直在2.15上下浮动,R2值的平均水平明显低于2009年之前。说明在网络复杂程度大幅提高以后,幂律函数模型更加容易受到特殊个体的干扰,对整体网络结构变动测度的准确性较为有限。从对数复合模型的结果来看,β值从2006年到2011年持续上升,之后到2015年持续下降,反映出教育联系网络演化的阶段性特征。在网络完善过程中由于少数名校辐射力强,节点度数很大,提高了整个网络的首位度和异质性,随后对外扩散的名校数量增加,度数差异减小,网络结构渐趋成熟,表明城市基础教育联系合作加强。相比之下,对数复合模型的R2值远高于幂律函数模型,数据平稳性更好,减少了拟合误差。说明逆序累积规模模型比位序规模法则更适于识别教育联系网络结构特征。
|
|
表 2 2006—2015年幂律函数模型和对数复合模型的回归结果 Table 2 Regression results of power-law function and logarithm-compound models from 2006 to 2015 |
公共服务设施的区位选择受到政治因素的约束[27],名校设置分校作为社会资源分配的内容也存在行政管理边界的分割和限制。选取2007、2011、2015年共3个典型年份数据,综合各类基础教育设施区内和区际扩散联系的网络密度,通过公式(3)测算整体边界效应,可衡量市辖区边界对优质教育资源扩散的影响。
边界效应的测度结果(表 3)显示,各市辖区之间边界效应对名校设置分校的扩张仍有一定限制作用,但随着城市教育网络的发展这种限制总体呈逐渐减弱的趋势。2007年,靠近市中心各行政区的边界效应较弱,边缘郊区则很强,中心-外围的结构特征突出,反映中心区域教育联系较为密切,而郊区由于河流、山脉等自然地理障碍和经济社会发展差距阻碍了教育联系;到2011年,除鼓楼区和浦口区外,中心区域的边界效应下降,边缘区域则上升,隔离度总体加强,其中鼓楼区由于将重点转向区内教育合作,故边界效应增强,浦口区由于跨江名校分校的迅速增加边界效应呈下降趋势;中心区域和边缘区域的边界效应差异在2015年显著缩小,雨花台区的边界效应有所下降但仍为最大,主要由于其以区内扩散为主导,外来名校分校较少,而秦淮区将教育合作重心转向加大区内教育资源整合力度,因此边界效应变强。可以预见,随着更多名校分校在雨花台和江宁规划建设,未来两区的边界效应将继续下降。
|
|
表 3 2007—2015年各区边界效应 Table 3 Border effects in different districts from 2007 to 2015 |
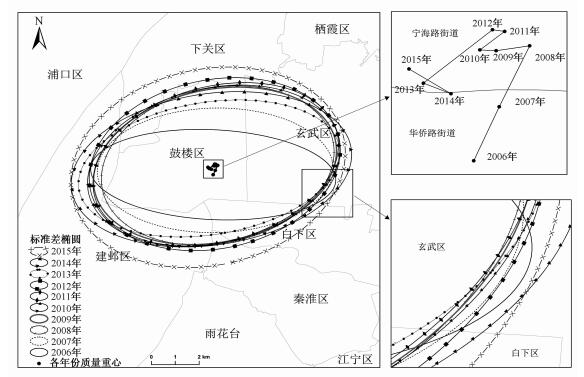
教育联系网络的增强和优化推动教育质量空间分布的均衡化趋势,并引起发展重心位置的变迁。一般用升学率和考试分数量化评估教学质量[28],因此指标方面,小学选择南京民众普遍认为的最佳初中南京外国语学校的录取率,初中选择中考平均分,高中选择高考平均分。采用极差标准化方法对指标数值进行无量纲化处理,指标权重用AHP方法确定,并用信息论中的熵技术对权重进行修正[29],确定小学至高中的权重依次为0.607, 0.271和0.122,据此计算出2006—2015年基础教育综合发展的质量重心并绘制出标准差椭圆的空间分布态势如图 4所示。
|
Download:
|
| 图 4 2006—2015年南京市教育质量重心及标准差椭圆分布 Fig. 4 Distribution of educational gravity and standard deviational ellipses of Nanjing from 2006 to 2015 | |
从重心分布来看,各时期中心在118°45.63′~45.89′E,32°3.27′~3.53′N之间变动,大致位于主城区中部稍偏西的区域,即鼓楼区东南部宁海路街道和华侨路街道交界处。从重心移动的轨迹来看,总体上质量重心向北偏西方向移动,10年移动距离为1.334 km,其中2006—2010年向北偏东移动0.396 km,2011—2015年向西南移动0.348 km,重心南北偏移的距离大于东西方向的距离。
从标准差椭圆分布态势来看,各年份的标准差椭圆均以该年份的重心为中心,位于主城中部偏西地区。10年内标准差椭圆总体上呈扩大态势,以老鼓楼区为核心,范围大致覆盖城墙以内的地区,基本上包括南京市基础教育最发达的地区。主轴延伸方向大致呈逆时针旋转的趋势,由2006年接近正东—正西方向变为2015年的东北—西南方向,表明总体上教学质量的空间分布呈现出东北—西南格局。在2006—2012年椭圆的辅半轴标准差增加,椭圆离心率减小,表明教育质量在西北—东南方向上出现分散;在2013—2014年辅半轴标准差减小,表明教育质量该时段在西北—东南方向上出现极化;2015年椭圆离心率又下降,教育质量在西北—东南方向上再度分散,且椭圆范围有继续扩大的趋势。
教育质量重心变化的主要成因是优质教育网络的扩散更加倾向于城市西侧的区域,特别是政府规划推动河西新城的建设,引入诸多名校进驻,老城区名校在河西等地设置分校时间较早、成果比较显著,使河西逐渐发展成为教育高地,而东部玄武区和南部秦淮区部分名校设置分校的成果尚未充分显现。
4 讨论与结论 4.1 讨论基础教育设施空间演化是复杂的变化过程,既有设施配置自身的自组织内在要求,又受外界影响。其区位选择一般普遍受到包括人口分布、就业布局和房地产投资等因素作用。在特定情形下,基础教育设施也会反过来影响人口集聚和房地产价值。可归纳为:
1) 常住人口呈持续增长态势。2006—2015年,栖霞、浦口、江宁、雨花台的常住人口年均增长分别为4.7%、3.5%、3.4%和3.9%,中小学及幼儿园在学人数的年均增长分别为4.9%、2.2%、2.8%和8.3%,成为基础教育设施演化至关重要的推动力。另一方面,基础教育设施特别是名校会吸引居民迁入,改变人口分布格局。例如,金陵中学、南师附中等名校在栖霞区办学推动该区域大量适龄人口集聚,促进人口增长。
2) 就业布局。就业布局在基础教育设施建立与演化中也发挥着重要作用,与人口分布一起共同影响着基础教育设施的集聚与扩散[9]。例如,仙林新城在建设基础教育设施的同时建立科技产业园区,拉动产业创造上下游岗位,缓解就业不足。教育设施和就业岗位的配套协调布局有利于提高公共空间的使用效率,促进城市经济发展,缓解交通压力。
3) 房地产投资。教育设施的可达性和质量对住房有较为显著的资本化作用[30]。根据哈维的空间生产理论[4],资本具有逐利的本性。因此开发商在投资房地产时会配建优质教育设施以打造“学区房”,提高楼盘的含金量。例如,金地集团在雨花台区的金地自在城楼盘开发中配建力学小学分校,引进外区名校资源改善当地教育质量,生产具有更高使用价值的空间产品,推动资本向获取更高利润的空间流动,实现房地产资本的增值。
4.2 结论本文基于多种GIS空间分析和社会网络分析方法,从数量、质量、空间联系等角度,对南京市基础教育设施空间结构特征的演化进行探讨。研究得出如下结论:
1) 2006—2015年,幼儿园和小学集聚性增强,初中和高中则减弱,表明不同等级设施存在局部可达性改善和总体数量均衡的目标差异;除初中外平均邻近距离下降,说明基础教育设施覆盖范围扩大。
2) 除高中外,各类设施高密度区域范围显著扩大,其中小学大致呈单核结构扩张,初中呈双核向三核转变的趋势,幼儿园在江宁区形成新的最高极值核,表明在新城建设等城市扩张发展过程中基础教育设施配套逐渐完善,以实现空间生产理论中资本的第3次循环。
3) 名校扩散的教育联系网络的发展从以近域扩散为主转为跨江扩散和向西南边缘区域扩散,网络异质性总体呈先升后降趋势,反映优质教育的分享范围扩大、作为中心节点的名校数量增加;内城弱、郊区强的边界效应差距先增后减,雨花台区边界效应始终最强,区内外合作倾向会影响边界效应,优质教育体系的中心-外围结构有所弱化但依然明显存在。
4) 教育质量的重心总体先向北后向西移动,椭圆西北—东南轴向集聚趋向弱化,离心率减小,但主要仍集中于鼓楼区,城市东部和南部的教育质量相对较低,反映基础教育设施数量和质量在空间上存在不匹配现象,优质教育网络的功能尚未充分显现。
据此,本文对改进南京市基础教育设施规划提出如下建议:①完善基础教育设施体系,优化初中布局,增强邻近度和可达性;②在满足数量的基础上,通过与市场力量的结合,加强浦口区、江宁区等边缘行政区自有名校和分校的建设,增加中心节点,促进优质教育网络的结构更加合理化,并合理配置教学资源,提升城市东部和南部的教学水平,推动基础教育质量均衡发展;③各市辖区发展本区教育要处理好区内整合教育资源与跨区开展教育合作的关系,推动城市教育协调发展,促进城市公共服务设施规划的空间公平。
| [1] |
宋正娜, 陈雯, 张桂香, 等. 公共服务设施空间可达性及其度量方法[J]. 地理科学进展, 2010, 29(10):1217–1224.
DOI:10.11820/dlkxjz.2010.10.009 |
| [2] |
Harvey D.
Social justice and the city[M]. Baltimore: The Johns Hopkins University Press, 1975.
|
| [3] |
Batley R, Mcloughlin C. The politics of public services:a service characteristics approach[J]. World Development, 2015(74):275–285.
|
| [4] |
Harvey D.
The urbanization of capital[M]. Oxford: Blackwell, 1985.
|
| [5] |
Li D, Wei Y D, Wang T. Spatial and temporal evolution of urban innovation network in China[J]. Habitat International, 2015(49):484–496.
|
| [6] |
胡思琪, 徐建刚, 张翔, 等. 基于时间可达性的教育设施布局均等化评价[J]. 规划师, 2012, 28(1):70–75.
|
| [7] |
胡梅梅. 大城市基础教育设施空间非均衡性研究: 以济南市中心区为例[D]. 济南: 山东建筑大学, 2014: 25-40.
http://cdmd.cnki.com.cn/Article/CDMD-10430-1015516821.htm |
| [8] |
张京祥, 葛志兵, 罗震东, 等. 城乡基本公共服务设施布局均等化研究:以常州市教育设施为例[J]. 城市规划, 2012, 36(2):9–15.
|
| [9] |
Zolnik E, Minde J, Gupta D D, et al. Supporting planning to co-locate public facilities:a case study from Loudoun County, Virginia[J]. Applied Geography, 2010, 30(4):687–696.
DOI:10.1016/j.apgeog.2010.01.006 |
| [10] |
韩高峰, 秦杨. 需求与供给分析视角下教育设施布局规划指标体系构建:以南康市中心城区中小学布局专项规划为例[J]. 规划师, 2013, 29(12):104–109.
DOI:10.3969/j.issn.1006-0022.2013.12.019 |
| [11] |
Taleai M, Sliuzas R, Flacke J. An integrated framework to evaluate the equity of urban public facilities using spatial multi-criteria analysis[J]. Cities, 2014, 40:56–69.
DOI:10.1016/j.cities.2014.04.006 |
| [12] |
谢婷婷, 冯长春, 杨永春. 河谷型城市教育设施空间分布公平性研究:以兰州市中学为例[J]. 城市发展研究, 2014, 21(8):64–67.
|
| [13] |
杜俊秀, 张继贤, 董春, 等. 中小学布局水平指标体系的空间均衡性分析[J]. 测绘科学, 2015, 40(7):64–67.
|
| [14] |
郭全. 基于GIS的城市基础教育资源布局均衡性研究: 以兰州市城关区中小学为例[D]. 兰州: 兰州大学, 2011: 27-60.
http://cdmd.cnki.com.cn/Article/CDMD-10730-1011139259.htm |
| [15] |
Terxeira J C, Antunes A P. A hierarchical location model for public facility planning[J]. European Journal of Operational Research, 2008, 185(1):92–104.
DOI:10.1016/j.ejor.2006.12.027 |
| [16] |
Dadashpoor H, Rostami F, Alizadeh B. Is inequality in the distribution of urban facilities inequitable? Exploring a method for identifying spatial inequity in an Iranian city[J]. Cities, 2016, 52:159–172.
DOI:10.1016/j.cities.2015.12.007 |
| [17] |
卢晓旭, 陆玉麒, 尚正永, 等. 学校体系规模调整和空间演化特征的测度与分析:以南京市普通高级中学为例[J]. 地理科学, 2011, 31(12):1454–1460.
|
| [18] |
赵晨旭, 邵景安, 郭跃, 等. 山区乡村学校空间格局演变特征及发展水平[J]. 地理研究, 2016, 35(3):455–470.
|
| [19] |
Clark P J, Evans F C. Distance to nearest neighbor as a measure of spatial relationships in populations[J]. Ecology, 1954, 35(4):445–453.
DOI:10.2307/1931034 |
| [20] |
袁丰, 魏也华, 陈雯, 等. 无锡城市制造业企业区位调整与苏南模式重组[J]. 地理科学, 2012, 32(4):401–408.
|
| [21] |
刘军.
整体网分析讲义:Ucinet软件实用指南[M]. 上海: 格致出版社, 2009: 56-107.
|
| [22] |
叶磊, 段学军, 欧向军. 基于社会网络分析的长三角地区功能多中心研究[J]. 中国科学院大学学报, 2016, 33(1):75–81.
|
| [23] |
李丹丹, 汪涛, 魏也华, 等. 中国城市尺度科学知识网络与技术知识网络结构的时空复杂性[J]. 地理研究, 2015, 34(3):525–540.
|
| [24] |
秦贤宏, 魏也华, 陈雯, 等. 南京都市区人口空间扩张与多中心化[J]. 地理研究, 2013, 32(4):711–719.
|
| [25] |
Wei Y D. Spatiality of regional inequality[J]. Applied Geography, 2015, 61:1–10.
DOI:10.1016/j.apgeog.2015.03.013 |
| [26] |
薛二勇. 基础教育名校办分校的政策分析:基于北京市基础教育均衡发展政策的调查研究[J]. 教育科学研究, 2014(7):45–50.
|
| [27] |
Deverteuil G. Reconsidering the legacy of urban public facility location theory in human geography[J]. Progress in Human Geography, 2000, 24(1):47–69.
DOI:10.1191/030913200668094045 |
| [28] |
Yinger J. Hedonic markets and sorting equilibria:bid-function envelopes for public services and neighborhood amenities[J]. Journal of Urban Economics, 2015, 86(3):9–25.
|
| [29] |
方创琳, 毛汉英. 区域发展规划指标体系建立方法探讨[J]. 地理学报, 1999, 54(5):410–419.
|
| [30] |
La V. Capitalization of school quality into housing prices:evidence from Boston public school district walk zones[J]. Economics Letters, 2015, 134:102–106.
DOI:10.1016/j.econlet.2015.07.001 |
 2018, Vol. 35
2018, Vol. 35 


