2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近些年,时间反转技术(time-reversal, TR)已经引起诸多学者的广泛关注,特别是时间反转在复杂环境中通信和超分辨率成像方面表现出来的潜力[1-2],在诸如探地雷达、医学影像、隐藏目标探测、大气及海洋干扰去除等领域具有很大的应用价值。其基本原理可以表述为,源点依次发射的电磁波信号被传感器阵列接收,接收的信号被阵元记录并进行时间反转(频域相共轭),再次发射到目标区域,则信号能量可以实现在目标处的重聚焦,这个发射-接收阵列叫做时间反转镜[3]。由于时间反转不需要介质性质及传感器阵列分布特性等先验知识就能实现自适应聚焦,因此在复杂环境中的应用具有很重要的价值。但是随机介质对时间反转的具体影响,还需要进一步的分析和研究。
目前,时间反转理论已经成功应用于声学领域,但是时间反转在电磁学领域整体应用仍需要完善的理论和数值仿真支持[3-6]。在传统的成像中,聚焦分辨率受传感器阵列尺寸限制。时间反转因为多路径效应,有效孔径反而比实际物理尺寸更大,尤其是在高度复杂的散射环境下,能实现超分辨聚焦[7-9]。此外,由于复杂环境的强散射,传统的方法(例如SAR)对随机介质中的物体进行成像时,成像质量会有严重的恶化,而时间反转则依然可以完成高质量的聚焦。因此,对于复杂环境中的目标探测而言,时间反转技术相比传统方法具备明显的优势。
本文主要根据文献[10]提出的理论方法,深入分析随机介质对TR聚焦成像的影响。该方法基于随机介质的统计特性[11-13],通过对互相干函数的简化,将随机介质效应表示为非相干项和相干项分量[14-16]。通过仿真实验,本文从TR平均场和强度两个方面分析随机介质对成像聚焦特性的影响,探讨光学厚度、TR对矩阵稀疏化的容忍度、随机介质位置及随机介质参数对TR聚焦效果的影响,为随机介质中超分辨率成像应用提供理论指导和支持。
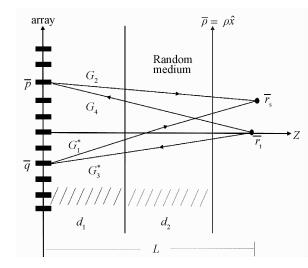
1 随机介质中物体散射成像理论 1.1 时间反转问题的总体表述如图 1所示,在点源处rt发射一束高斯脉冲,该波束被M接收阵元接收,时间反转,后向传播进同一个介质中,在rs处进行观测。d1为阵列到随机介质的位置,d2为随机介质的厚度。
|
Download:
|
| 图 1 时间反转成像几何示意图 Fig. 1 Geometry of time reversal imaging | |
考虑上述问题,发射阵元依次发射高斯脉冲,电磁波穿过随机介质层后,到达散射点源rt处,反射后被所有阵元接收。接收阵元将回波信号时间反转后同时发射,电磁波将在散射点源区域时-空同步聚焦。成像处理,即在信号处理的维度完成这一过程,其中,引入成像点rs。聚焦成像后,在接近rt的rs位置,图像的强度更大。在该场景中,发射阵元p=mh0,接收阵元q=nh0,为避免栅瓣,阵元间距h0=λ0/2,在rt(L, 0)处,点源高斯模拟脉冲f(t)和其频谱F(ω)为
| $\begin{array}{l} \quad f\left( t \right) = {A_0}{\rm{exp}}\left( { - \frac{{{t^2}}}{{T_0^2}} - {\rm{i}}{\omega _0}t} \right),\\ F\left( \omega \right) = {A_0}\frac{{2\sqrt {\rm{ \mathit{ π} }} }}{{\Delta \omega }}{\rm{exp}}\left( { - \frac{{{{(\omega - {\omega _0})}^2}}}{{\Delta {\omega ^2}}}} \right). \end{array}$ | (1) |
式中:Δω=2/T0是带宽;ω0是载频;在点(L, 0)处发射和在(p, 0)接收的波束表达为格林函数G1,场G1被时间反转(等同于频域共轭G1*),将反转的信号发射到同一个介质中。时间反转的信号频谱是原始信号的复共轭。在rs处的场是所有M个阵元接收信号之和。其频谱表达为
| $\begin{array}{l} \psi ({{\bar r}_{\rm{s}}},\omega ) = \sum\limits_{\rm{m}} {\psi ({{\bar r}_{\rm{s}}},{{\bar r}_{\rm{m}}},{{\bar r}_{\rm{t}}},\omega )} ,{{\bar r}_{\rm{m}}} = \bar p = p\hat x,\\ \psi ({{\bar r}_{\rm{s}}},{{\bar r}_{\rm{m}}},{{\bar r}_{\rm{t}}},\omega ) = {G_2}({{\bar r}_{\rm{s}}},{{\bar r}_{\rm{m}}},\omega )G_1^*({{\bar r}_{\rm{s}}},{{\bar r}_{\rm{m}}},\omega ){F^*}(\omega ). \end{array}$ | (2) |
因此,时间反转的平均场可以表达为
| $\begin{array}{l} \left\langle {\psi \left( {\bar r,{\rm{ }}{t_{\rm{s}}}} \right)} \right\rangle = \frac{1}{{2{\rm{ \mathit{ π} }}}}\int {{\rm{exp}}\left( { - {\rm{i}}\omega t} \right){\rm{d}}\omega } \sum\limits_{\rm{m}} {\left\langle {\psi \left( {{{\bar r}_{\rm{s}}},{{\bar r}_{\rm{m}}},{{\bar r}_{\rm{t}}},{\rm{ }}\omega } \right)} \right\rangle } \\ = \frac{1}{{2{\rm{ \mathit{ π} }}}}\int {{\rm{exp}}( - {\rm{i}}\omega t){\rm{d}}\omega } \sum\limits_{\rm{m}} {{\mathit{\Gamma }_{\rm{m}}}({{\bar r}_{\rm{s}}},{{\bar r}_{\rm{m}}},{{\bar r}_{\rm{t}}},{\rm{ }}\omega ){F^*}\left( \omega \right)} , \end{array}$ | (3) |
式中:Γm是互相干函数MCF(mutual coherence function)Γm=〈G2(rs, rm, ω)G1*(rs, rm, ω)〉.
在rs的场为G1*G2, 因此,时间反转强度为〈(G1*G2)(G3*G4)*〉, 其中(G1*G2)使用频率ω1,(G3*G4)使用频率ω2,该过程表示TR成像的具体物理过程。
| $\begin{array}{l} \left\langle {\psi ({{\bar r}_{\rm{s}}},{\rm{ }}{t_1}){\psi ^*}({{\bar r}_{\rm{s}}},{\rm{ }}{t_2})} \right\rangle = \frac{1}{{{{(2{\rm{ \mathit{ π} }})}^2}}}\int {{\rm{d}}{\omega _1}{\rm{d}}{\omega _2}\mathit{\Gamma }({\omega _1},{\omega _2})} \cdot \\ \quad \quad \quad F({\omega _1}){F^*}({\omega _2}){\rm{exp}}( - {\rm{i}}{\omega _1}t + {\rm{i}}{\omega _2}t), \end{array}$ | (4) |
其中,
如果可以得到MCF,则可利用式(3)、式(4)得到统计性的聚焦效果,即时间反转平均场和强度。
1.2 互相干函数基于格林函数在分析场景下的抛物线近似,可以将式(3)中的MCF表达为
| ${\mathit{\Gamma }_{\rm{m}}} = \frac{1}{{{{(4{\rm{ \mathit{ π} }}L)}^2}}}{\rm{exp}}\left[ {{\rm{i}}\frac{k}{L}\left( {\frac{{{{\bar \rho }_{\rm{s}}}}}{2} - \bar p} \right) \cdot {{\bar \rho }_{\rm{s}}} - H({{\bar \rho }_{\rm{s}}})} \right],$ | (5) |
其中,函数H(ρs)代表随机介质效应,对于随机分布的粒子[10-12]
| $H({{\bar \rho }_{\rm{s}}}) = \int_{{d_1}}^{{d_2}} {{\rm{d}}z'} \left\{ {a + b\int_0^2 {\frac{1}{2}p\left( s \right)\left[ {1 - {J_0}\left( {ksP} \right)} \right]} } \right\},$ | (6) |
式中:a(z′)和b(z′)分别是吸收和散射系数;p(s)是单一粒子散射相函数;s=2sin(θ/2),θ是散射角。为方便起见,把随机介质效应分为相干和非相干两部分,p(s)假定是高斯分布
| $p\left( s \right) = 4{\alpha _{\rm{P}}}\exp \left( {{\alpha _{\rm{P}}}{s^2}} \right).$ | (7) |
因此,可以近似表达式exp(-H)
| ${\rm{exp}}\left( { - H} \right) = {\rm{exp}}\left( { - H} \right) = {\rm{exp}}( - {\tau _0}) + {F_{\rm{s}}}X,$ | (8) |
式中:
对于TR强度,MFC可以使用圆复高斯(circular complex Gaussian assumption)假设将四阶矩表达为二阶矩。该假设经常用来描述随机介质中波束的扰动。
| $\begin{array}{l} \left\langle {G_1^*{G_2}{G_3}G_4^*} \right\rangle = \left\langle {G_1^*{G_2}} \right\rangle \left\langle {{G_3}G_4^*} \right\rangle + \left\langle {G_1^*{G_3}} \right\rangle \\ \quad \quad \left\langle {{G_2}G_4^*} \right\rangle - \left\langle {G_1^*} \right\rangle \left\langle {{G_2}} \right\rangle \left\langle {{G_3}} \right\rangle \left\langle {G_4^*} \right\rangle . \end{array}$ | (9) |
使用式(9),可以获得粒子的随机分布
| $\begin{array}{l} \left\langle {G_1^*{G_2}{G_3}G_4^*} \right\rangle = \left[ {G_{10}^*{G_{20}}{G_{30}}G_{40}^*} \right]\left[ {{\rm{exp}}\left( { - {H_{21}} - {H_{34}}} \right) + } \right.\\ \quad \quad {\rm{exp}}( - {H_{31}} - {H_{24}}) - {\rm{exp}}( - 2{\tau _0})]. \end{array}$ | (10) |
式中:[G10*G20G30G40*]是自由空间格林函数;Hij代表随机介质效应;因子exp(-Hij)同样可以表达为相干和非相干分量之和。
以上分析中,τ0, τs, τa分别表示光学厚度、光学散射厚度和光学吸收厚度。光学厚度等同于粒子密度,为单一粒子总的散射截面积和距离的乘积。粒子密度是指单位体积内粒子的数量。光学厚度可以表征相干强度的消减,表示为平均自由路径的距离。光学散射厚度和光学厚度计算方式是一样的,只不过使用散射截面积代替总的截面积。散射厚度等同于散射截面积和总的截面积之比。对于给定的介质,该比值是定值,因此散射厚度正比于光学厚度。在本文的计算中,我们变化光学厚度,相当于变化散射厚度。同理,吸收深度表示为吸收截面积和总的截面积之比。从中可以看出,相干和非相干强度正比于exp(-τ0)和exp(-Qij)-exp(-τ0)。ρ0指相干长度,表示为距离的函数,是指非相干强度减少到峰值的exp(-1)的值。关于该模型更详细的描述,可参考文献[16]。
2 数值仿真与讨论基于上节给出的理论模型,通过参数分析的方式,讨论不同OD条件下阵列稀疏化、不同随机介质位置、不同随机介质参数对成像聚焦效果的影响。使用以下参数作为数值仿真的例子:L=50λ, d1=25λ,d2=25λ,αp=44.58,N=M=10, h0=λ/2,和Δω/ω0=0.05。
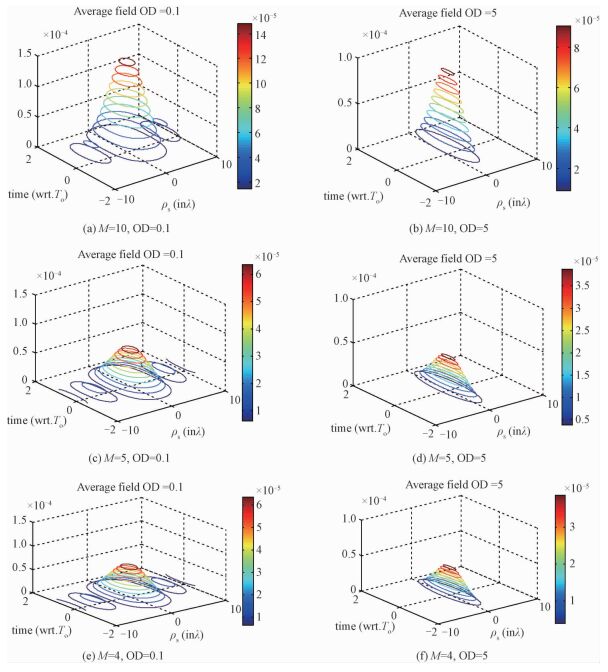
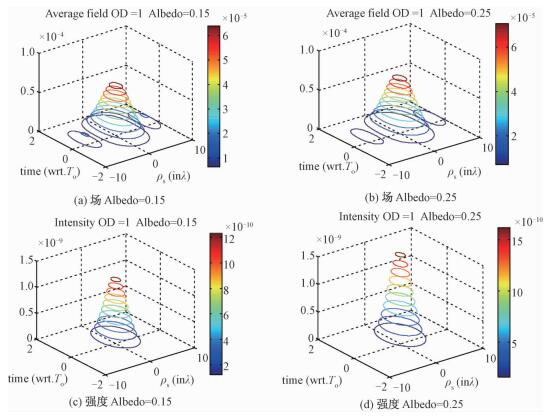
图 2~图 5中TR聚焦的平均场和强度分布可表示为横向位置ρs和时间t的函数。因为散射厚度正比于光学厚度,论文中给定不同的光学厚度,可以得到随机介质不同的散射强度。在光学厚度OD=0.1时,随机介质层的散射强度很小,近似于自由空间;在OD=5时,随机介质多次散射比较明显,对物体散射信号具有较强的影响。图 4和图 5中使用OD=1,因为该情况下图像具有典型的聚焦效果,可以方便其他变量的比较。
|
Download:
|
| 图 2 不同光学厚度及阵元稀疏情况下TR平均场仿真结果 Fig. 2 TR average field simulation results with different optical depths in different array sparsity cases | |
|
Download:
|
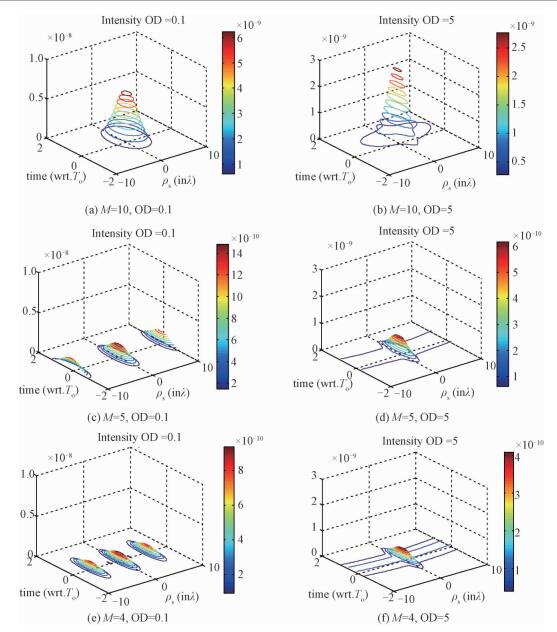
| 图 3 不同光学厚度及阵元稀疏情况下TR强度仿真结果 Fig. 3 TR intensity simulation results with different optical depths in different array sparsity cases | |
|
Download:
|
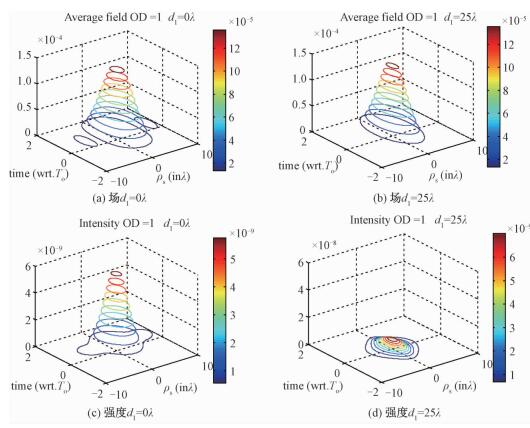
| 图 4 随机介质不同位置TR仿真结果,平均场和强度 Fig. 4 TR simulation results at varying locations in different average field and intensity conditions | |
|
Download:
|
| 图 5 不同反照率TR仿真结果,平均场和强度 Fig. 5 TR simulation results with different albedos in different average field and intensity conditions | |
图 2分别给出光学厚度为OD=0.1和OD=5时的平均场的聚焦对比图,并且在相同的天线阵列长度下,将阵元进行稀疏化,即扩大阵元间距为一个波长,如图 2(b)和2(d)所示, 并且进一步稀疏化为阵元数为4的情况,如图 2(e)和2(f)。以此比较TR方法对稀疏化的敏感度。分别对比图 2(a)和2(c)、图 2(b)和2(d)可以看出,在近似自由空间情况(OD=0.1)下,阵列稀疏化使得TR的副瓣情况更加明显,同时因为阵列接收的能量变小,其幅值有明显下降。分别对比图 2(a)和2(b)、图 2(c)和2(d)可以得出,光学厚度OD的增大,TR平均场聚焦效果变得更好,体现为主瓣更窄,并且在大的光学厚度下,随机介质的加入对副瓣也有抑制和消除作用。分别对比图 2(c)和2(e)、图 2(d)和2(f)可以发现,虽然在一定的稀疏情况下,时间反转方法具有一定的容忍度,但是当通道数减少为4个阵元时,该成像方法聚焦效果不是很理想,综合观测口径和减少栅瓣干扰角度,还需要借助矩阵稀疏化理论进一步研究改进。
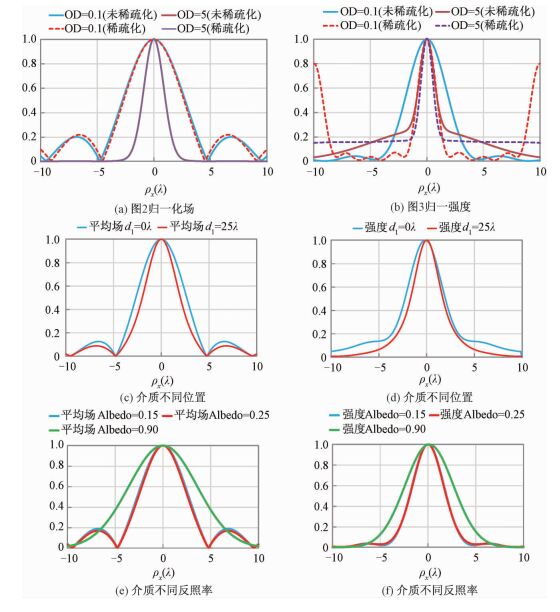
图 3给出和图 2类似的对比情况,即OD增加,散射强度变大,但是其接收信号变弱,幅度值变小,在稀疏化的情况下,图 3(c)和3(e)中出现聚焦的混叠现象,图 3(d)和3(f)中图像也表现出部分不能汇聚。虽然因为接收能量变小其幅度值下降明显,但是在随机介质加入后,相比于自由空间,TR还是具有明显的聚焦效果,体现出在阵列稀疏情况下,对复杂环境具有较好的容忍度。通过图 6(a)和6(b)的折线图可以看出,随机介质的引入使得图像聚焦效果更好,表现为在水平方向上的汇聚。体现在式(9)中的第2项给出的前向和后向波束的相关性,该项体现“后向散射加强”,复杂的介质反而加强了聚焦和成像质量,突显出“超分辨率”特性。但是也会造成信噪比下降,因为随机介质散射变强,物体散射信号相对较弱,所以稀疏化阵列的强度图像,在大的OD情况下仍会出现图中的线不收敛。
|
Download:
|
| 图 6 不同参数条件下分辨率对比 Fig. 6 Resolution comparision among different parameter conditions | |
图 4给出随机介质的位置效应对TR平均场及强度的影响,该现象即“浴室窗帘效应”。具体表现为随机介质离物体位置越近,物体和介质的散射信号贡献越大,对成像聚焦效果越好。d1=0λ时,随机介质离阵列位置比较近,d1=25λ时,随机介质离阵列比较远,散射目标在随机介质中。对比图 4(a)、4(b)和图 4(c)、4(d)并结合图 6(b)、6(c)表明:当物体在随机介质中时,TR的聚焦反而比在自由空间中的效果好。
图 5分析随机介质参数反照率对聚焦效果的影响,反照率越高,表示随机介质中的散射越强。参考3种典型地物的反照率经验值,即草地(0.15)、植被(0.25)和冰雪(0.9),结合图(6)归一化分辨率对比图 6(e)、6(f)从中发现,地物复杂程度越高,对介质中物体的探测反而具有更好的效果。综合图 2、图 4和图 5不难发现:当物体在随机介质中时,在一定条件下,随机介质的散射强度越高,TR技术中物体的聚焦和成像效果越好。
从以上不同的仿真图中可以看出,随机介质的存在引起TR的超分辨聚焦,并且随机介质的散射强度越大,在目标的聚焦效果更好。由于随机介质的引入,改变了物体的散射信号传播路径,产生多路径的效果,从而使天线的实际有效孔径变大。同时通过上述多个参数的分析可以看出,TR在复杂环境中对物体的聚焦具有一定的容忍度。可见,复杂环境中TR技术在超分辨率方面具有明显的优势,有潜力应对复杂环境中的探测需求。
3 结论本文基于随机介质中时间反转的理论方法,从不同角度进一步分析和验证TR方法在复杂环境中物体成像方面的优势,即随机介质中的散射强度越高,TR技术中物体的聚焦和成像效果越好,在稀疏阵列的情况下也具有明显的效果。本文研究为随机介质中物体的探测和成像实际应用提供了理论支撑和参数参考。随后的研究工作将逐步深入讨论随机介质的具体参数以及多目标之间散射的交互性和相关性等问题。
| [1] |
Lerosey G, De Rosny J, Tourin A, et al. Time reversal of electromagnetic waves[J]. Physical Review Letters, 2004, 92(19):193904.
DOI:10.1103/PhysRevLett.92.193904 |
| [2] |
Lerosey G, De Rosny J, Tourin A, et al. Time reversal of electromagnetic waves and telecommunication[J]. Radio Science, 2005, 40(6):RS6S12.
|
| [3] |
Fink M. Time reversed acoustics[J]. Physics Today, 1997, 50(3):34–40.
DOI:10.1063/1.881692 |
| [4] |
Borcea L, Papanicolaou G, Tsogka C, et al. Imaging and time reversal in random media[J]. Inverse Problems, 2002, 18(5):1247.
DOI:10.1088/0266-5611/18/5/303 |
| [5] |
Derode A, Tourin A, Fink M. Random multiple scattering of ultrasound. I. Coherent and ballistic waves[J]. Physical Review E, 2001, 64(3):036605.
DOI:10.1103/PhysRevE.64.036605 |
| [6] |
Derode A, Tourin A, Fink M. Random multiple scattering of ultrasound. Ⅱ. Is time reversal a self-averaging process[J]. Physical Review E, 2001, 64(3):036606.
DOI:10.1103/PhysRevE.64.036606 |
| [7] |
Blomgren P, Papanicolaou G, Zhao H. Super-resolution in time-reversal acoustics[J]. The Journal of the Acoustical Society of America, 2002, 111(1):230–248.
DOI:10.1121/1.1421342 |
| [8] |
Lerosey G, De Rosny J, Tourin A, et al. Time reversal of electromagnetic waves[J]. Physical Review Letters, 2004, 92(19):193904.
DOI:10.1103/PhysRevLett.92.193904 |
| [9] |
Liu D, Vasudevan S, Krolik J, et al. Electromagnetic time-reversal source localization in changing media:Experiment and analysis[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(2):344–354.
DOI:10.1109/TAP.2006.889807 |
| [10] |
Ishimaru A, Jaruwatanadilok S, Kuga Y. Time reversal effects in random scattering media on superresolution, shower curtain effects, and backscattering enhancement[J]. Radio Science, 2007, 42(42):507–530.
|
| [11] |
Ishimaru A, Jaruwatanadilok S, Kuga Y. Multiple scattering effects on the radar cross section (RCS) of objects in a random medium including back-scattering enhancement and shower curtain effects[J]. Waves in Random Media, 2004, 14(4):499–512.
DOI:10.1088/0959-7174/14/4/002 |
| [12] |
Ishimaru A, Jaruwatanadilok S, Kuga Y. Short pulse detection and imaging of objects behind obscuring random layers[J]. Waves in Random and Complex Media, 2006, 16(4):509–520.
DOI:10.1080/17455030500486759 |
| [13] |
Ishimaru A, Jaruwatanadilok S, Kuga Y. Imaging of a target through random media using a short-pulse focused beam[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(6):1622–1629.
DOI:10.1109/TAP.2007.897318 |
| [14] |
Liu D, Vasudevan S, Krolik J, et al. Electromagnetic time-reversal source localization in changing media:Experiment and analysis[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(2):344–354.
DOI:10.1109/TAP.2006.889807 |
| [15] |
Goodman J W, Narducci L M. Statistical Optics[J]. Physics Today, 1986, 39(10):126–126.
|
| [16] |
Ishimaru A.
Wave propagation and scattering in random media[M]. New York: Academic Press, 1978.
|
 2018, Vol. 35
2018, Vol. 35 


